基于机舱传递函数的风机功率曲线研究

杨明明

（华润电力技术研究院有限公司，广东深圳518002）

0 引言

中国风电产业正处于迅猛发展的阶段，截至2019 年上半年，中国已并网风电装机容量达到了193 GW，占全国能源总装机的10.5%，位居全球第一［1］。因此，针对已经投运的风电场进行发电性能评估、技术改造、性能优化等工作具有重要意义，值得高度关注［2］。已投运风电机组性能评估的一个重要指标就是功率曲线是否符合预期，这也是验证风电场设计发电量与实际发电量差异的一个重要环节。但是现有的功率曲线测试一般只选取风电场的某一台风电机配置测风设备进行功率特性评估，并以此结果来代表整个风电场的评估结果。该结果无法代表风电场所有风电机组的性能，存在很大的经济隐患。基于机舱传递函数的功率曲线以其高效、快速以及全面等特点成为研究重点［3］。目前，国内外基于机舱传递函数的功率曲线研究也取得了一定的进展:IEC 61400-12-2 采用机组机舱风速计计算机组功率特性的多段分区法，采用Bin 法计算测量风速与机舱功率的功率曲线［4-5］；张双益等［6］在此标准的基础上，采用了双机舱传递函数（Nacelle Transfer Function，NTF）修正机舱风速中的湍流影响，修正结果比IEC 标准给出的原始方法要更准确。高峰等［7］突破标准中机舱风速传递函数的简单线性拟合法，利用测风塔数据，以高阶多项式建立机舱风速的传递函数关系，优化效果明显。

基于机舱传递函数的功率曲线计算关键在于机舱风速与自由流风速函数关系的建立。本文针对主要的机舱传递函数计算方法进行剖析，通过工程实例量化各方法下的发电量误差以及实测风速拟合偏差，对比各机舱传递函数计算方法的优劣。

1 主要机舱传递函数计算方法

1.1 动量理论修正法

基于风轮动量理论的单元流管模型［8-9］，可将风轮后的机舱风速修正成风轮前的自由流风速。如图1 所示，设通过风轮的气流上游截面积为A1，下游截面积为A2，风轮截面积为A；v1，v2，v分别为上述3个位置对应的风速。假设机舱风速接近于v2，自由流风速接近于v1，v即为v1和v2的平均值。因风轮吸收的能量等于风轮前后气流动能之差，机组发电功率可表示为

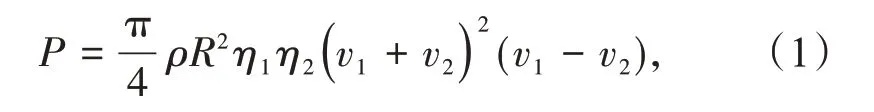
式中:ρ为空气密度；R为风轮半径；η1为机组传动链效率；η2为发电机效率。

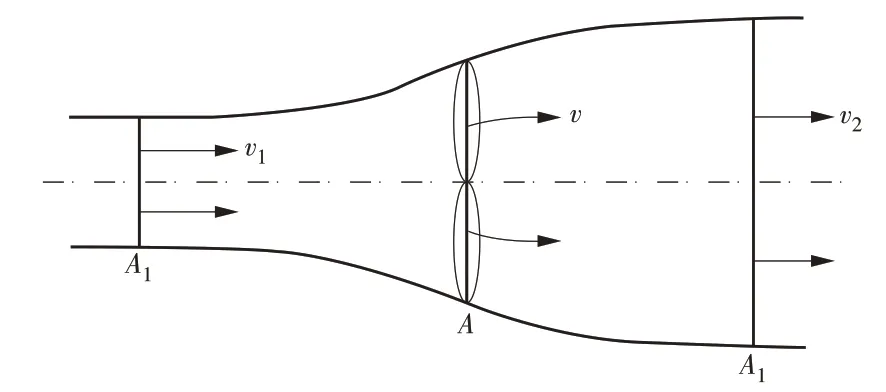
图1 风力发电机气流流动过程示意Fig.1 Air flow in a wind turbine

1.2 分区多段线性拟合Binned-NTF修正法

构造机舱风速与自由流风速之间最优拟合关系宜采用Binned-NTF修正法，即按照不同的风速区间拟合NTF 的方法。参考IEC 61400-12-2中的Bin法，将风速按0.5 m/s 为间隔分成若干Bin 区间，每个Bin 区间中心值为0.5 m/s 的整数倍［10］。利用下式分别计算出每个Bin 区间的机舱风速均值和测风塔风速均值，

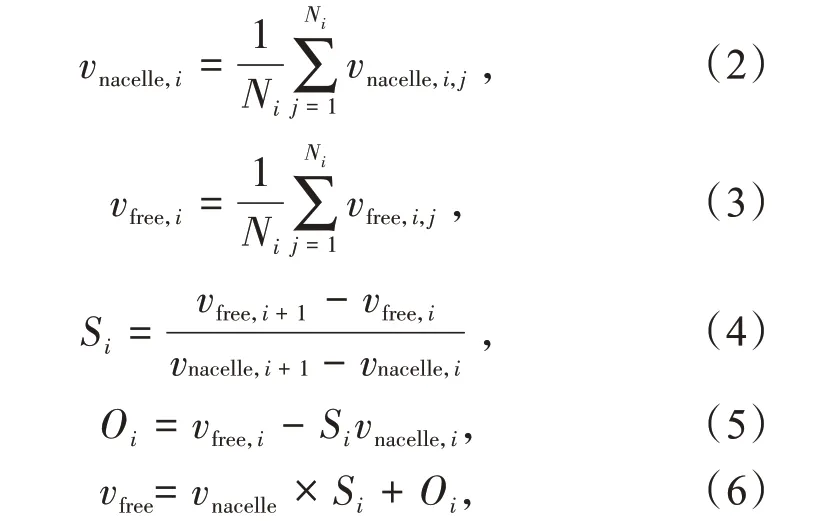
式中:vnacelle，i为落在第i个Bin 区间的机舱风速平均值；vnacelle，i，j为落在第i个Bin 区间第j组的机舱风速；Ni为落在第i个Bin 区间的测量数据对的数量；vfree，i为落在第i个Bin区间的自由流风速平均值；vfree，i，j为落在第i个Bin 区间第j组的自由流风速；Si为第i个Bin 区间的斜率；Oi为第i个Bin 区间的偏移量；vfree为自由流风速；vnacelle为机舱风速。

1.3 高次多项式分区拟合修正法

本方法主要根据依据机组控制策略的不同分将风速分为低于额定风速区间和高于额定风速区，同时在各区间内采用高阶多项式分别进行拟合。

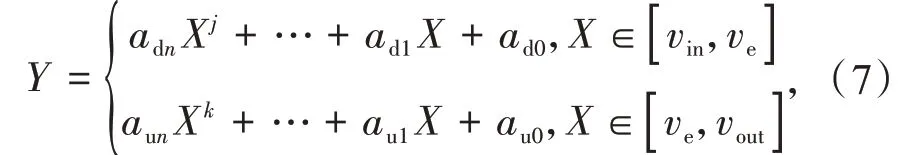
式中:X为机舱风速；Y为自由流风速；j，k为拟合函数的阶数；vin为切入风速；vout为切出风速；ve为额度风速。

2 工程实例

2.1 项目概况

某平原风电场主要以低矮农作物和杂草等为主要植被，主风向位于45°∼180°之间，测试期间以南风为主，激光雷达位于测试机位东南侧250 m 处，相对位置如图2所示。

图2 激光雷达与风机的相对位置Fig.2 Relative position of LiDAR and wind turbines

根据IEC 61400-12-2 标准对试验机位进行地形评估，对场地的地形复杂度指数（RIX0.04）和倾角进行计算，测试机组地形参数见表1。根据IEC 61400-12-2 附录B，该测试机组地形为地形分类中1 类地形，符合使用NTF 函数计算和传统功率曲线测试的地形要求。

表1 测试机组地形参数Tab.1 Terrain parameters of the tested wind turbines

根据IEC 61400-12-2 附录A 对测试机组障碍物进行评估。该风场内主要障碍物为风电机组，计算出测试机组D34有效扇区为0°∼100°，300°∼350°，根据筛选出的有效扇区数据，进行机舱传递函数的计算。

2.2 数据采集

对该平原风场的25 台WTG2000-104 型机组进行数据采集，包括:通过数据采集与监视控制系统（SCADA 系统）采集的2018 年11 月—2019 年10 月风机10 min 平均风速和功率；机组主要性能参数；2019 年4 月20 日—7 月14 日 激 光 雷 达80 m 高 处 的10 min 平均风速、风向。将机舱风速和激光雷达数据按6∶2∶2 分成训练集、验证集和测试集。训练集和验证集用于机舱传递函数的计算，测试集用于各方法的结果分析。

2.3 实例结果分析

对测试机组SCADA 系统的10 min 平均机舱风速分别采用分区多段线性拟合Binned-NTF修正法、高次多项式分区拟合修正法和理论修正法计算机舱传递函数、求导自由流风速，3 种计算方式的比较结果见表2。

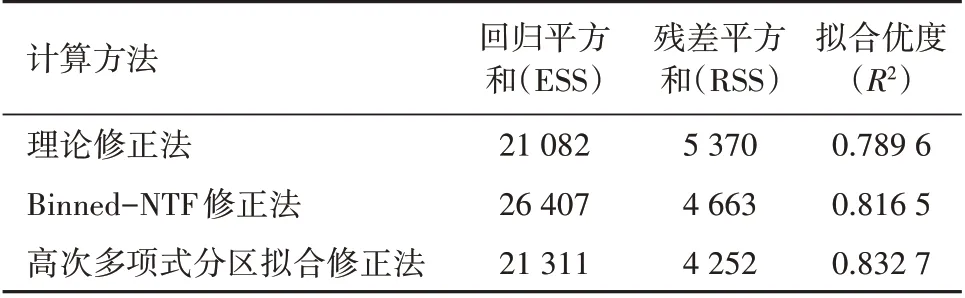
表2 3种计算方式比较Tab.2 Results of three computing mode

就ESS 而言，分区多段线性拟合Binned-NTF 修正法得到的结果最大，说明其与实测风速的拟合情况优于另外2 种修正法；就RSS 而言，数值较小的方法拟合程度更优，高次多项式分区拟合修正法和分区多段线性拟合Binned-NTF修正法的数值相当，而理论修正法的数值较大；从R2来看，3 种方法的差异较小，高次多项式分区拟合修正法略优于另外2 种修正法，相关性如图3—5所示。

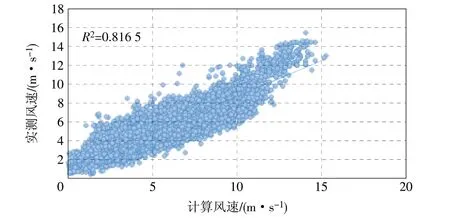
图3 实测值与Binned-NTF修正法计算值相关性Fig.3 Correlation between measured value and calculated value of Binned NTF correction method

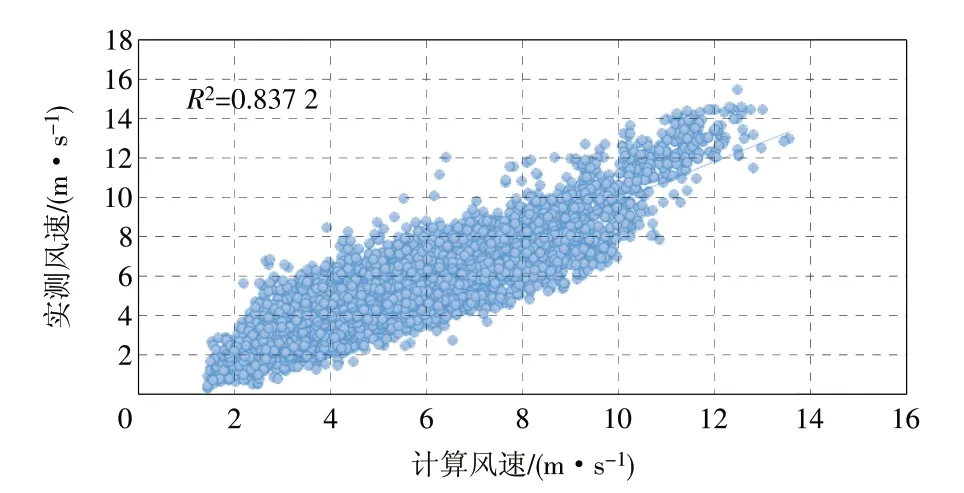
图4 实测值与高次多项式分区拟合修正法计算值相关性Fig.4 Correlation between measured value and calculated value of high degree polynomial partition fitting correction method

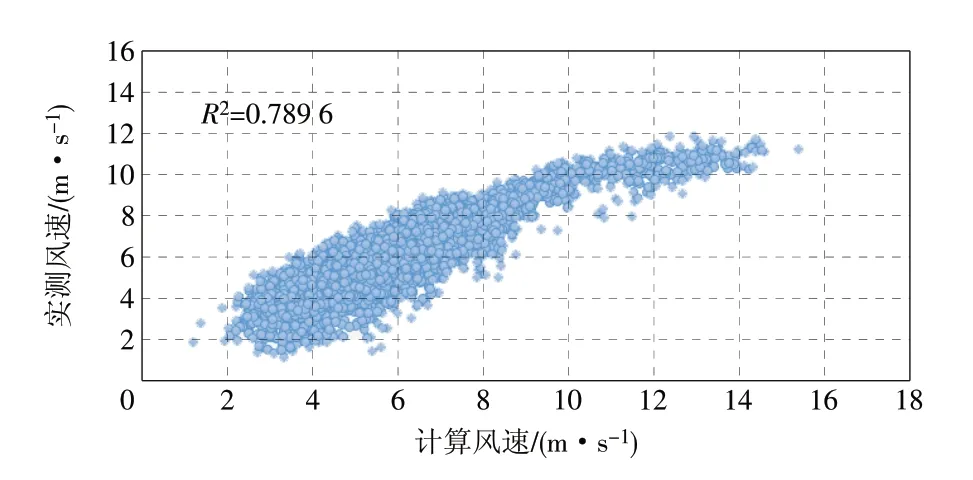
图5 实测值与理论修正法计算值相关性Fig.5 Correlation between measured value and calculated value of theoretical correction method

综合来看，高次多项式分区拟合修正法最优，而分区多段线性拟合Binned-NTF 修正法又优于理论修正法。因此，应优先采用实测拟合的高次多项式分区拟合修正法计算平原风电场机舱传递函数。

采用Bin 法绘制、比较机组的测试功率曲线和利用不同修正法计算出的功率曲线，如图6 所示。从图6 中可以看出，分区多段线性拟合Binned-NTF修正法和理论修正法的功率曲线较为一致，高次多项式分区拟合修正法比较接近测试功率曲线［11-12］。

功率曲线对机组性能的评价体现于机组发电效益［13-15］，本文利用场内测风塔风频进行发电量计算，统计各方法的发电量与实测功率曲线的发电量的误差［16-20］。从表3 中可以看出，拟合法与实测功率曲线的发电量误差率在-2.33%～4.14%之间，理论修正法的发电量误差率略大，超过5%。分区多段线性拟合Binned-NTF 修正法和高次多项式分区拟合修正法的误差在5%以内，理论修正法误差率略大于5%。整体来看，受机舱风速仪测量精度的影响，3 种机舱传递函数方法计算的功率曲线与实测功率曲线均存在一定的偏差，但误差率较小。其中高次多项式分区拟合修正法的误差率最低，仅为-2.33%，明显优于其他2 种机舱传递函数计算方法。

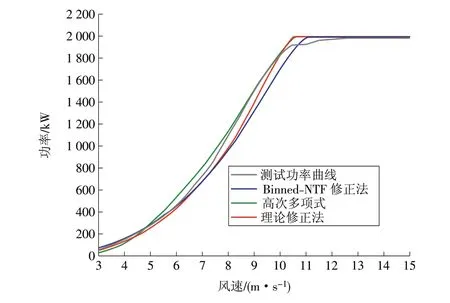
图6 功率曲线对比Fig.6 Power curve comparison

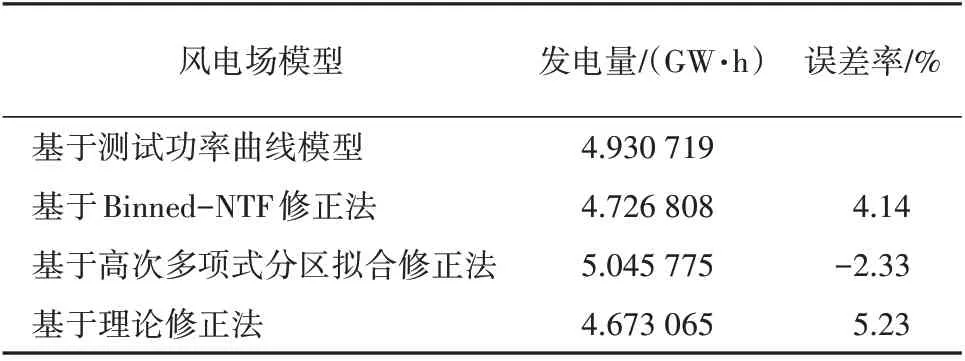
表3 计算功率曲线与测试功率曲线发电量对比结果Tab.3 comparison results of power generation between calculated power curve and tested power curve

3 结论

（1）通过对3种主要机舱传递函数进行分析，机舱传递函数较传统功率曲线测试（只选取某一台风机配置测风设备）具有高效、快速以及全面的特点。

（2）受机舱风速仪测量精度以及自由流测风时长等因素的影响，某平原风电场采用3 种机舱传递函数计算的功率曲线均与实际发电量存在一定的误差，但误差在5%以内。

（3）从风速的拟合精度以及发电量的误差来看，拟合方法优于理论修正法，而拟合方法中高次多项式分区拟合修正法优于分区多段线性拟合Binned-NTF修正法。

（4）理论修正法误差大于拟合法的，原因在于该方法种将机舱风速等同于下截面风速，但是实际中机舱风速仪离叶轮较近，在节流效应的作用下能量损失未能体现，机舱风速与下截面风速存在偏差，甚至会高于下截面风速。同时，风速仪的精度对结果也有着较大影响。