抛物槽式集热器双轴跟踪方式性能研究

张智，孙杰，祁昊均

（西安交通大学化学工程与技术学院，西安710049）

1 问题的提出

目前，全球一次能源消费中传统化石能源依旧处于主导地位，但事实上，全球能源结构正在发生深刻的改变。如2015 年，全球一次能源消费仅增长了1.0%，远低于10 年平均水平1.9%，这是自1998年以来的最低增长率。而可再生能源发电量增长了15.2%，其增量创历史新高，几乎是全球发电量的全部增量。因此，在未来的能源领域中，可再生能源具有巨大的发展潜力。可再生能源中的太阳能具有资源丰富、分布广泛、环保、安全等特点，成为目前世界上最清洁、最现实、大规模开发利用最有前景的可再生能源之一。国际能源署发布的《世界能源展望2017 中国特别报道》预测:中国能源结构将逐渐转变为清洁发电，强有力的政策扶持与市场推动将继续降低可再生能源的成本，其中太阳能光热发电在2040年之后将在能源结构中占主导地位。能源结构预测如图1所示［1］。

图1 能源结构预测Fig.1 Forecast of the energy structure

在太阳能利用技术中，抛物槽式集热技术是目前主要应用于大规模中温型集热系统的集热技术，也是目前太阳能热发电技术中相对比较成熟且已实现商业化的一项技术。槽式集热器是槽式太阳能集热系统的核心元件，需要时刻跟踪太阳位置以保证聚光。传统抛物槽式集热器为单轴跟踪策略，以抛物线顶点所在线为轴，采用南北轴或东西轴布置，使跟踪系统始终保持太阳在抛物槽中心面上，从而保证最大的太阳辐射投入面积，但会存在余弦效应导致的余弦损失。而以双轴跟踪策略为基础，可以使抛物槽面接收太阳辐射的角度始终最优，消除余弦损失。但具体实施时往往对资金和工程技术要求较高，且会受到不同地理位置的影响。因此，根据不同地理因素设计合理的跟踪策略，对实际的跟踪和工程应用均具有重要意义。

2 数理模型与计算方法

2.1 连续投影算法

本文主要针对抛物槽式集热器的双轴跟踪方式开展研究。首先需要对抛物槽式集热器接收太阳辐射过程进行建模与计算，在建立理论直射辐射强度（Direct Normal Irradiance，DNI）计算模型前，需要计算天顶角与太阳方位角，以完成对太阳的定位。 连 续 投 影 算 法（Successive Projections Algorithm，SPA）提供了一个精确的太阳位置计算方法，从公元前2000 年到公元6000 年的不确定度仅为±0.000 3°。这种算法以世界时间（Universal Time，UT），即格林尼治公民时间为计算标准，因此，对不同经度的地区进行计算时，需要考虑时区，将当地时间转化为UT 后再进行计算。除时间变量外，地区的经纬度、年平均温度和气压、海拔都是必要的输入量。SPA 流程如图2所示［2］。

SPA 除了可以计算太阳天顶角，还可计算理论太阳日出、日落时间。但计算得到的理论高度角在一天中的每一时刻都有一个非零值，这与事实不符，因为一天中日出前及日落后高度角为零。因此，理论计算后，可根据日出日落时间对天顶角进行修正。日出与日落时间计算流程如图3所示［2］。

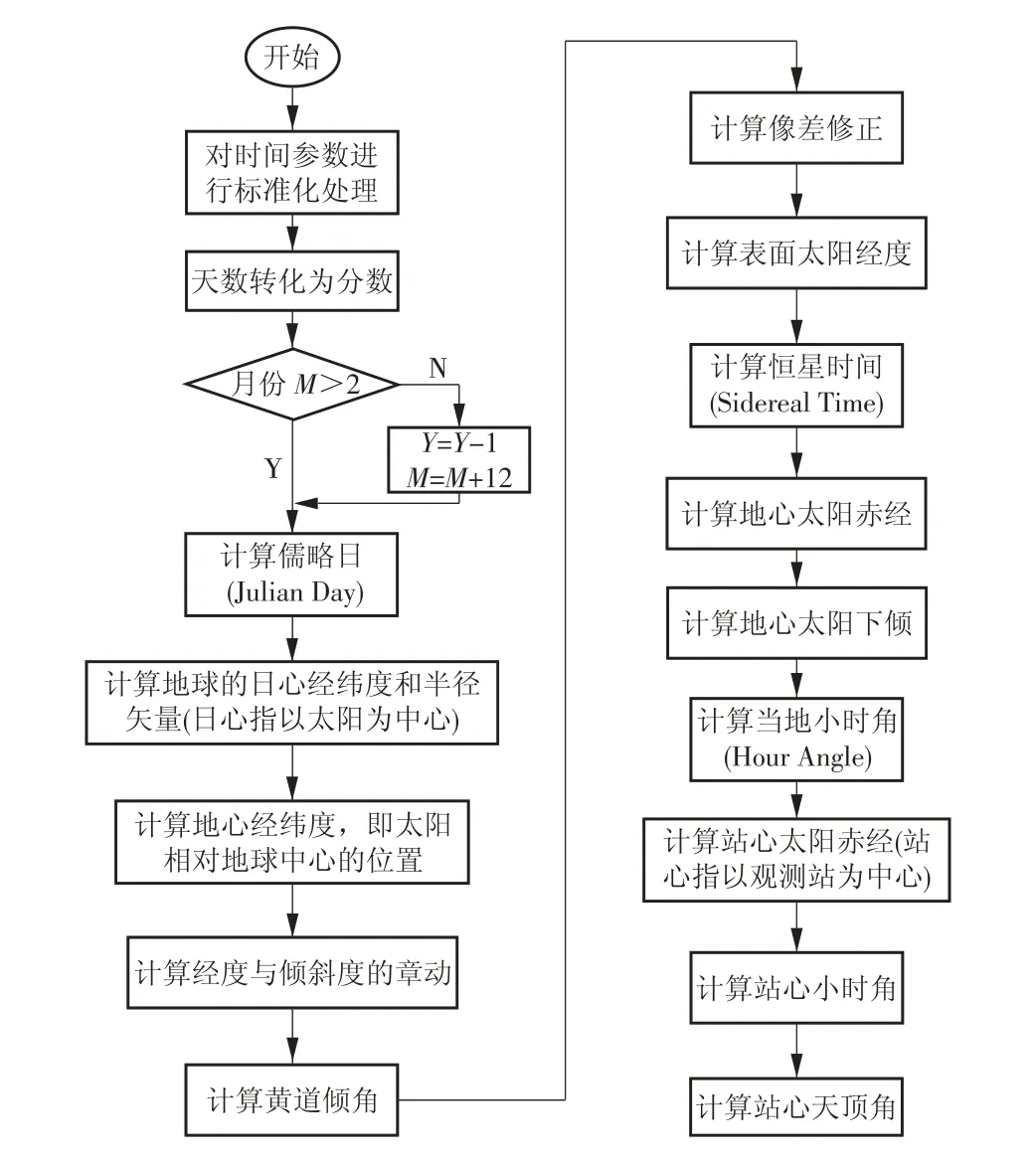
图2 SPA 流程Fig.2 Flow of SPA

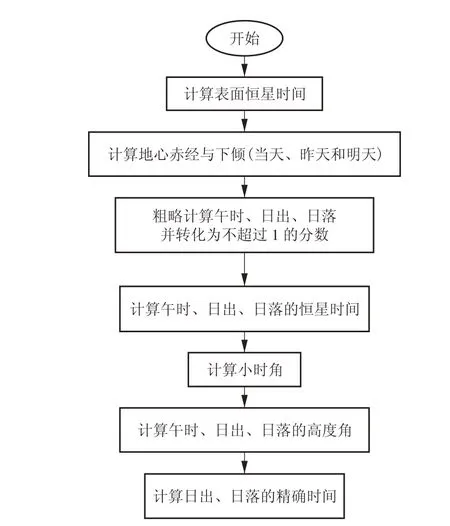
图3 日出与日落时间计算流程Fig.3 Calculation flow of sunrise and sunset time

2.2 理论DNI计算模型

理论DNI值Etheo计算公式如下［3］

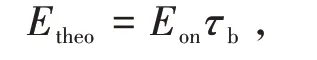
式中:Etheo为理论直射辐射强度，W/m2；Eon为大气层外太阳辐射强度，W/m2；τb为大气透射率。

式中:Esc为太阳常数［4］，1 367 W/m2；N为天序数。

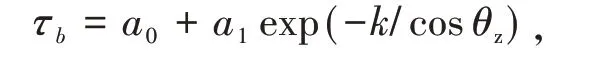
式中:a0，a1，k为修正系数；θz为天顶角，其值由SPA算法确定。

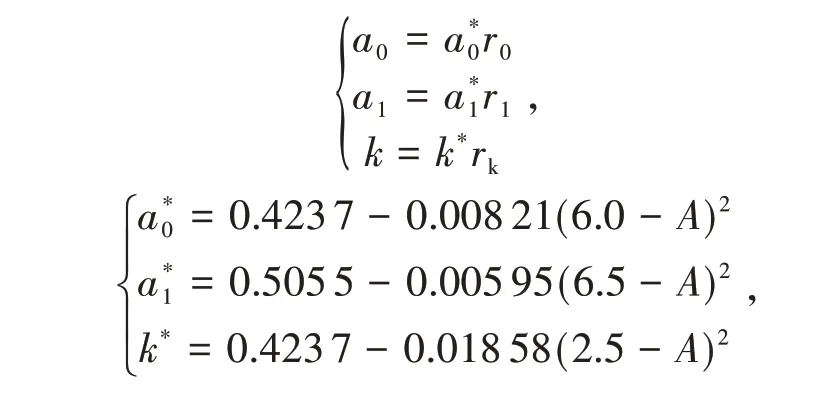
式中:r0，r1，rk为气象因素修正系数；A为海拔，km。

理论DNI值需要地理、气象因素的修正，不同的气候类型下修正系数不同，见表1［5］。需要说明的是，该理论DNI 值只考虑天气状况为晴而不考虑多云、雨等其他天气情况。

2.3 理论DNI计算程序验证

结合以上理论设计完成基于Matlab的DNI计算程序编写后，本小节对本文计算结果与文献中的结果进行对比，以验证程序计算结果的准确性。

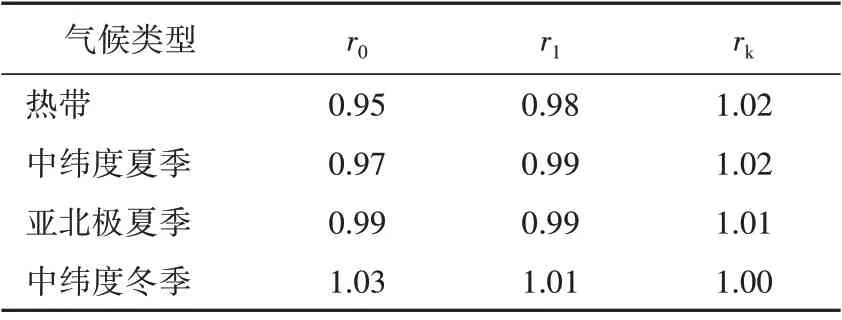
表1 不同气候类型下的修正系数Tab.1 Correction coefficients under different climate types

图4 为文献［6］中已有计算结果，图5 为本文计算结果。通过对比图4、图5 可知，本文计算结果与文献计算结果十分接近。分析出现偏差的原因，主要在于计算天顶角与方位角的方法不同。由此可见，该计算程序具有一定的精确性，可用于之后的计算。

图4 文献［6］中的全年逐时理论DNI分布Fig.4 DNI distribution according to hourly theory throughout a year recorded in literature［6］

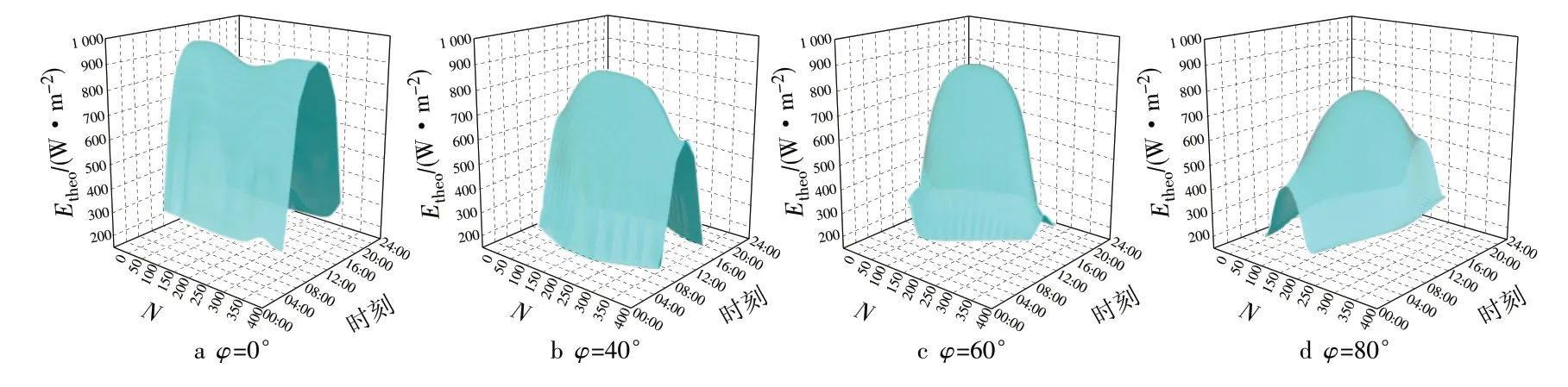
图5 本程序计算所得的全年逐时理论DNI分布Fig.5 DNI distribution according to hourly theory throughout a year based on the developed program

3 地理因素对抛物槽式集热器双轴跟踪性能的影响

3.1 地理因素对单位面积全年累积接收太阳辐射总量Ψ的影响

针对不同的纬度，计算分析双轴跟踪抛物槽式集热器的Ψ随海拔A的变化规律，如图6 所示。由图6 可以看出:随着海拔的上升，Ψ先上升，到达一个峰值后开始下降；在海拔达3 800 m 左右时，不同纬度下的Ψ近乎相同；之后，纬度越高Ψ越小。

3.2 地理因素对全年单位面积接收太阳辐射量Ψd分布的影响

分别计算分析不同纬度φ、不同海拔下Ψd的分布规律，结果如图7 所示。纬度较低时Ψd分布较为均匀，纬度较高时Ψd则变化较大。

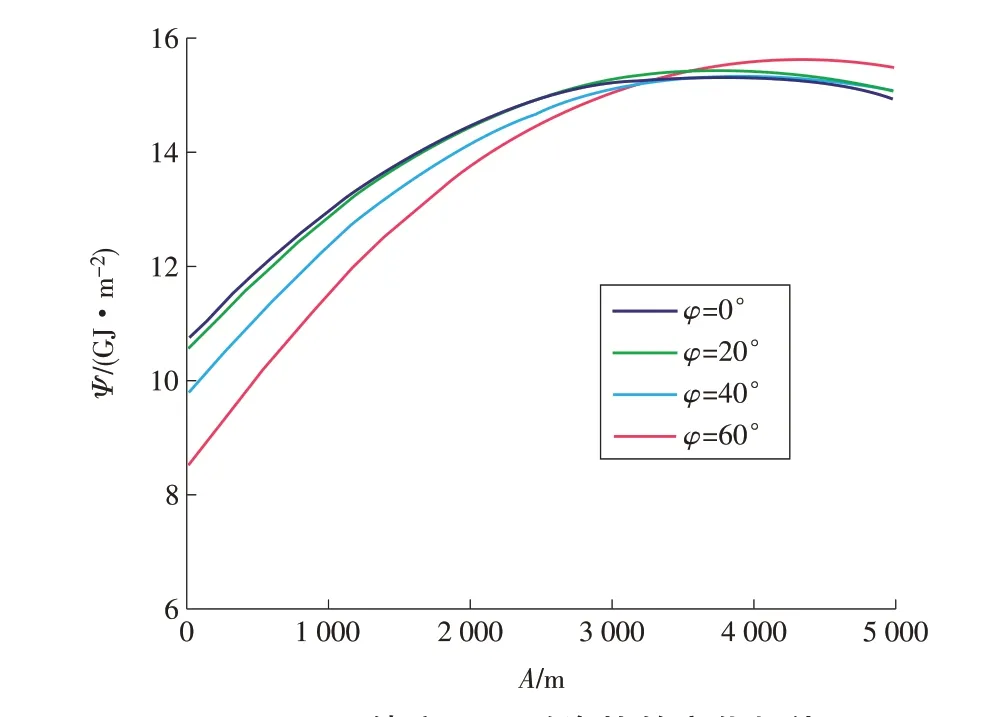
图6 不同纬度下Ψ随海拔的变化规律Fig.6 Variation of Ψ changing with latitudes at different altitudes

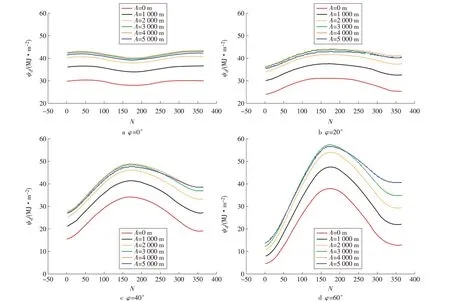
图7 不同纬度、不同海拔下Ψd的分布规律Fig.7 Distributions of Ψd at different altitudes and latitudes

φ=0°时Ψd有2 个峰值，海拔相同的条件下，Ψd的极差为3.5 MJ/m²；φ=20°时，Ψd先增加，之后近似不变，最后减少，海拔相同的条件下，Ψd的极差为5.0 MJ/m²；φ=40°时，Ψd先增加，之后增长速率变慢，到达峰值后开始减小，海拔相同的条件下，Ψd的极差约为17.0 MJ/m²；φ=60°时，Ψd先增加，之后下降，最后趋于平缓，海拔相同的条件下，Ψd的极差存在一定差别，海拔较低时极差为33.0 MJ/m²，海拔较高时极差为44.0 MJ/m²。

4 几何受限条件下抛物槽式集热器跟踪模式优化

针对城镇土地资源宝贵导致的区域几何受限情况，寻找抛物槽式集热器在几何受限条件下的最优跟踪方式具有重要意义。

本研究的几何受限区域是指总面积S一定，2条边长分别平行于南北轴线和东西轴线且具有单连通性质的矩形区域。研究的主要跟踪方式为单轴跟踪（东西方向和南北方向）、双排单轴跟踪（东西方向和南北方向）、3 排单轴跟踪（东西方向和南北方向）以及双轴跟踪，通过分析各跟踪方式下全年累积有效太阳辐射量Q和全年有效太阳辐射量的分布规律来寻求最优跟踪方式。

本文选取总面积为2 500 m²的方形区域，以南北方向边长lN-S与东西方向边长lW-E的比r（lN-S/lW-E）为自变量，计算分析r值不同时，不同跟踪方式下Q和全年有效太阳辐射量的分布规律，并进行方案对比评估以及经济性、环境性分析。

4.1 不同跟踪方式下的Q值

在几何受限条件下，以Q为指标，对抛物槽式集热器的不同跟踪方式进行评估。通过图8可以很直观地看出不同纬度、不同跟踪方式下Q与r的关系（图中:1AN-S为南北方向布置的单轴；1AW-E为东西方向布置的单轴；2×1AN-S为南北方向布置的双排单轴；2×1AW-E为东西方向布置的双排单轴；3×1AN-S为南北方向布置的3 排单轴；3×1AW-E为东西方向布置的3 排单轴；2A 为双轴）。整体而言，当r小于1 时，1AW-E跟 踪 相 比1AN-S跟 踪 较 优；当r大 于1 时，南1AN-S跟踪相比1AW-E跟踪较优。同样方位下的单轴跟踪，排数越多，Q越大。而双轴跟踪的Q一般小于单轴跟踪，但r在1附近时，纬度较高时Q更大。

因此，r小于1 时，可选择3×1AW-E跟踪；r在1 附近时，对于低纬度可选择3×1AN-S跟踪，高纬度可选择双轴跟踪；r大于1时，可选择3×1AN-S跟踪。

4.2 不同跟踪方式下全年接收太阳辐射量分布的均匀度

图8 不同纬度、不同跟踪方式下Q与r的关系Fig.8 Relationship between Q and r under different latitudes and tracking methods

变异系数可表示一组数据的离散程度，用标准差比均值来表示。本小节通过计算分析不同纬度、不同跟踪方式下，不同r值对应的全年接收太阳辐射量的变异系数Cv来评估其分布的均匀性，如图9所示。对于单轴跟踪，单排（东西方向和南北方向）的Cv对任意纬度均为常数，东西方向的Cv小于南北方向。随着纬度的上升，Cv整体上升。当全年累积接收太阳辐射量相近时，单轴追踪的集热器排数越多，Cv越大。而双轴跟踪的Cv随纬度、r不规则变化。

4.3 环境性与经济性分析

4.3.1 环境性分析

相比于传统火力发电厂，采用太阳能集热器集热可以减少CO2，NOx与SO2的排放。本小节针对不同跟踪模式的集热器，分别计算全年CO2，NOx与SO2的减排量。根据文献［7］，不同气体的等效减排量m可分别表示为

式中:Qc为输出相同电量时，火力发电厂依靠化石燃料需要提供的热量，kJ；fCO2，fNOx，fSO2分别为CO2，NOx，SO2排放因子；ηSO2，ηNOx分别为SO2，NOx的减排效率，%。

对单轴跟踪与双轴跟踪，Qc的计算可表示为

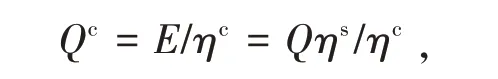
式中:E为等效全年发电量，kW·h；Q为全年太阳能集热量，kJ；ηs为抛物槽式太阳能电厂效率［8］，14%；ηc为火电厂效率［9］，38%。

选取φ=40°，r=1 的条件，计算几何受限时不同跟踪方式下全年减少排放CO2，NOx与SO2的情况，其结果如图10所示。

对比图10 与图8 中相同地理条件下全年累积接收太阳辐射总量图可知:全年减排量与全年累积接收太阳辐射总量Q成正比。φ=40°，r=1 时，全年累积接收太阳辐射总量大小关系与全年减排量关系一致，均为:3×1AN-S＞3×1AW-E＞2A＞2×1AN-S＞2×1AW-E＞1AN-S＞1AW-E。

4.3.2 经济性分析

本小节分析不同跟踪方式下抛物槽式集热器1年的经济效益。定义单位接收太阳辐射量所需费用为L，可表示为［10］

式中:EQ为全年累积太阳辐射总量，kW/m2；fcr为资本回收率［11］，9.88%；Cin为投资建造费用，欧元；Com为操作与维护费用，欧元。

同样选取φ=40°，r=1 的条件，计算几何受限时不同跟踪方式下一年平均单位接收太阳辐射量所需费用，结果如图11 所示。从计算结果可以看出，在φ=40°，r=1 时，双轴跟踪具有最低的年平均单位接收太阳辐射量所需费用。南北方向布置相比东西方向布置所需L更低。

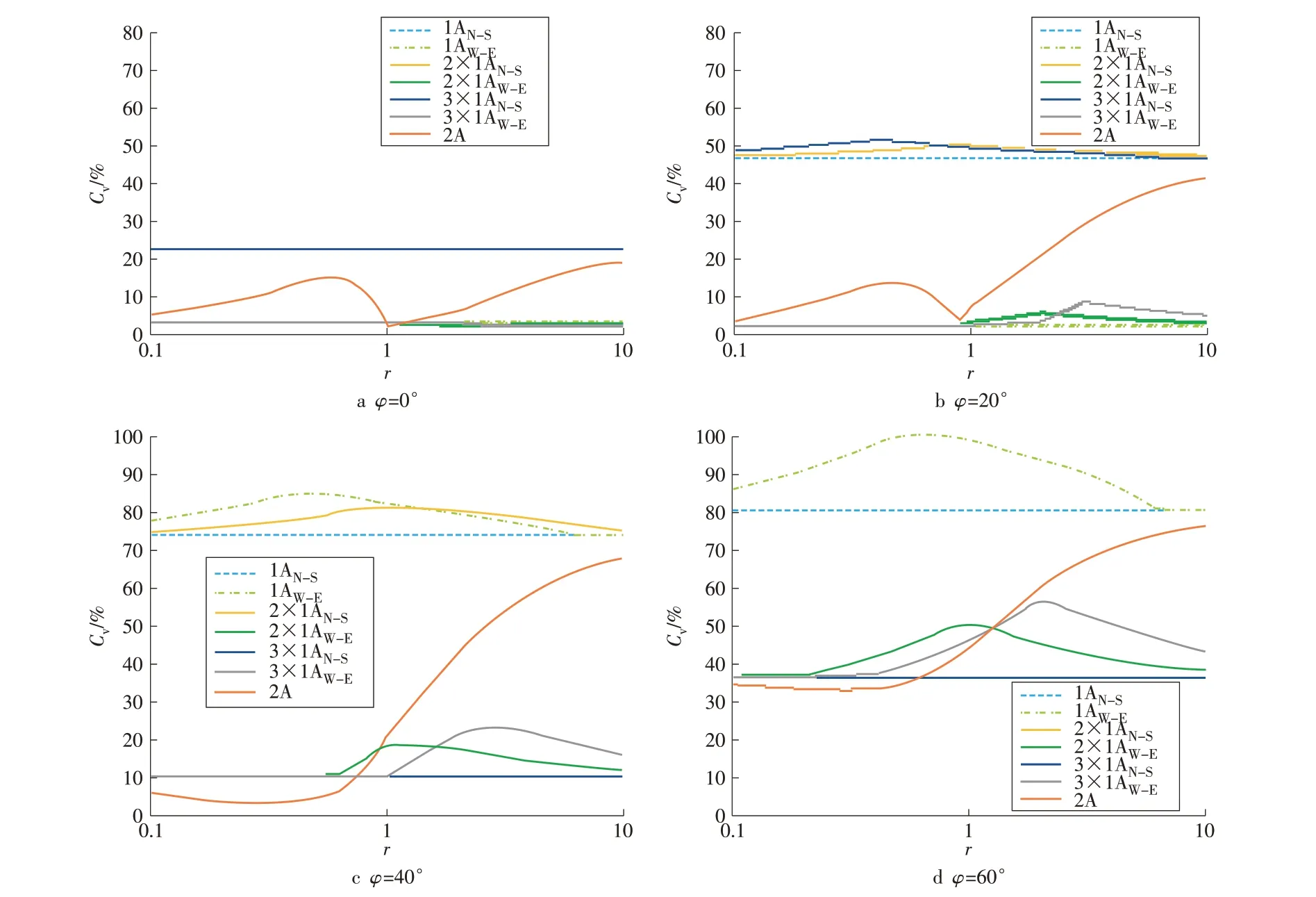
图9 不同纬度、不同跟踪方式下Cv与r的关系Fig.9 Relationship between Cv and r under different latitudes and tracking methods

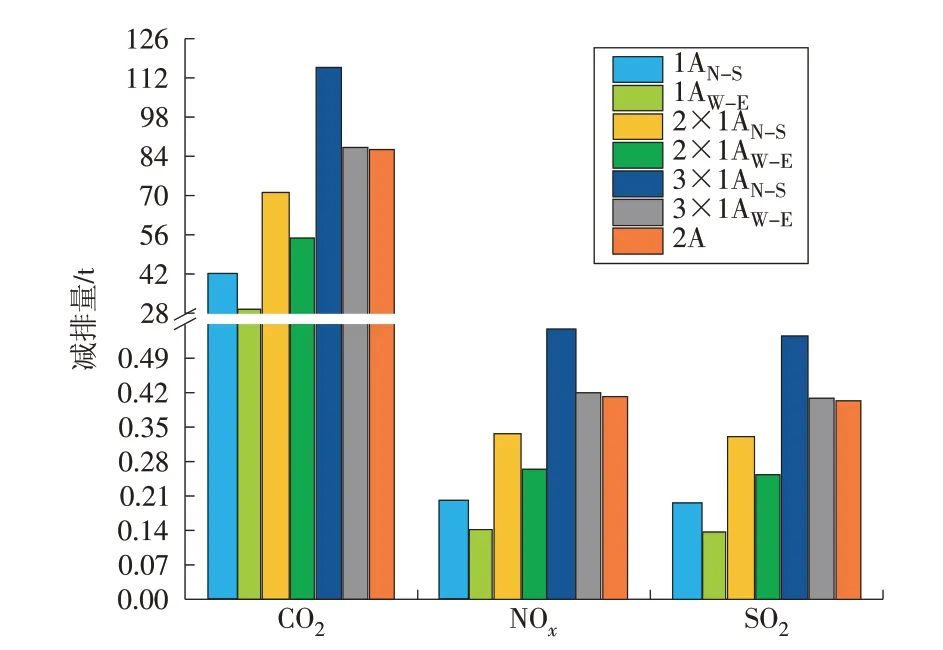
图10 几何受限时不同跟踪方式下全年减排量对比Fig.10 Annual emission reduction varying with different tracking methods under geometrically constrained condition

图11 几何受限时不同跟踪方式下的L值Fig.11 L value by different tracking methods under geometrically constrained condition

5 结论

本文主要针对抛物槽式集热器展开研究，对抛物槽式集热器接收太阳辐射量进行了建模与计算，开发了基于Matlab 的抛物槽式集热器逐时集热量模拟程序，并对程序进行了验证。然后分析了地理因素对抛物槽式集热器的双轴跟踪性能产生的影响，并对几何受限条件下的抛物槽式集热器不同的跟踪方式进行了评估与优化，结论如下。

（1）研究了地理因素对抛物槽式集热器双轴跟踪性能的影响，发现随着海拔的升高，全年累积接收太阳辐射总量先上升，在达到峰值后开始下降。随着纬度的升高，全年累积接收太阳辐射量分布的不均匀性增强。

（2）对比分析了几何受限时的不同跟踪方式，得到了不同边长比下的最优跟踪方式。边长比小于1 时，东西布置的3 排单轴跟踪全年累积接收太阳辐射量最高；边长比在1附近时，在低纬度下选择南北布置的3排单轴跟踪，高纬度下选择双轴跟踪；边长比大于1时，选择南北布置的3排单轴跟踪。

（3）分析几何受限时不同追踪方式下的全年接收太阳辐射量分布均匀度，发现单排单轴跟踪时变异系数在任意纬度下均为常数，东西方向布置的变异系数小于南北方向布置。当全年累积接收太阳辐射量接近时，集热器排数越多，变异系数越大，且随着纬度的增加，变异系数整体上升。对于双轴跟踪，边长比大于1 后，变异系数迅速上升，且随着纬度的增大变异系数增大。

（4）在选定地理条件下，通过环境性分析发现，全年减排量与全年累积接收太阳辐射总量成正比；经济性分析结果显示，双轴跟踪具有最低的年平均单位接收太阳辐射量费用，南北方向布置比东西方向布置所需要的费用更低。