基于模糊神经网络的枸杞滴灌系统设计

张 硕，王福平，胡永乐，李振翔

(1.北方民族大学计算机科学与工程学院，银川 750021；2.北方民族大学创新创业学院，银川 750021)

0 引 言

枸杞(Lycium barbarumL.)作为宁夏人民的主要经济来源之一，一直被广泛种植。但是在枸杞滴灌过程中一直采用的都是人工控制，自动化水平不高，容易造成水资源的浪费，或者没有满足枸杞生长所需要的水分，造成枸杞果实品质差。

针对以上缺点，设计了一种基于模糊神经网络的算法，将土壤湿度的偏差变化率及偏差作为输入，通过模糊神经网络对PID控制器的三个参数进行优化，实现枸杞滴灌时间的控制，最后使用Simulink搭建PID和模糊神经网络PID控制系统仿真模型，进行分析。

1 枸杞滴灌控制原理

枸杞滴灌主要受土壤湿度变化的影响[1]，并且枸杞在不同的生长周期需水量不同[2]，通过测量枸杞生长环境的土壤湿度，然后根据土壤湿度变化实现对枸杞滴灌时间的控制，保证枸杞生长在适宜的土壤湿度中。

1.1 PID控制原理

PID控制系统主要由控制器和被控对象两部分组成[3]。PID控制器将积分，偏差比例，微分三者结合，实现对被控对象的控制，控制原理如图1所示。

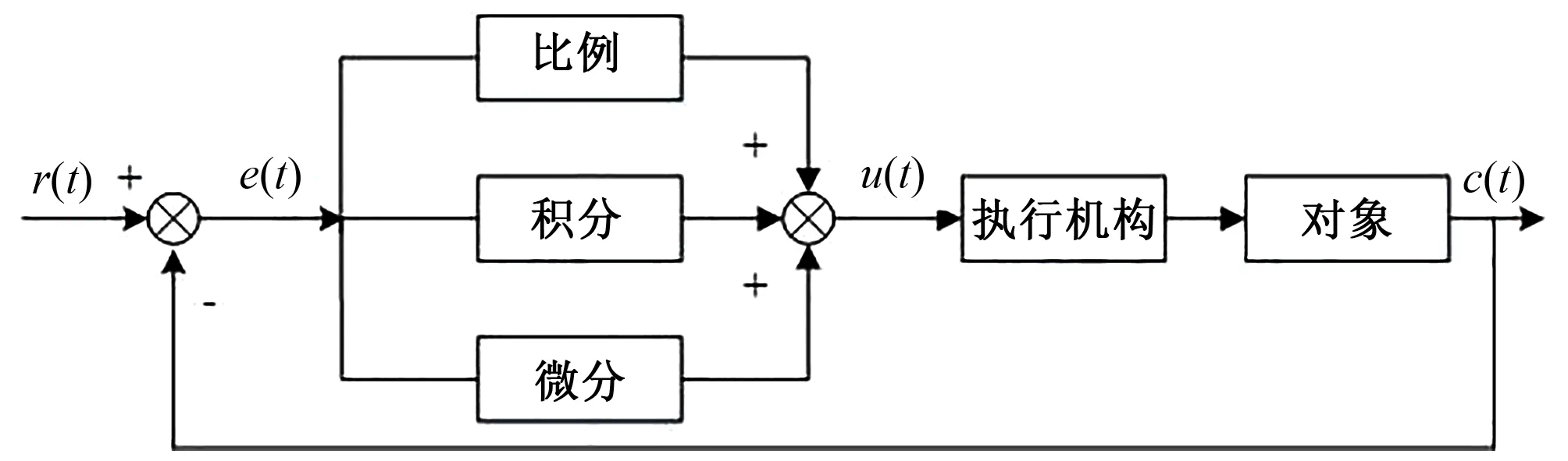
图1 PID控制原理

r(t)为输入量，c(t)为输出量，u(t)为控制量，e(t)为控制偏差，则：

e(t)=r(t)-c(t)

(1)

PID的表达式:

(2)

式中：TI为积分时间常数；KP为比例系数；TD微分时间常数；t为时间间隔。

KP可以快速地产生控制作用，并且可以成比例地反映控制系统的偏差信号e(t)，KP逐渐增大，稳态误差逐渐减小，但是震荡比较严重。TI主要作用是去除稳态误差，TI越大，积分作用越弱，过小的TI会使系统震荡严重。TD提高了系统的稳定性和响应速度，还反映了偏差信号e(t)的变化。

位置型PID算法是PID算法的一种形式[4]，位置型PID的数学表达式为：

式中：KI=KPT/TI为积分系数；KP为比例系数；KD=KPT/TD为微分系数；T为采样周期；输出u(k)可直接作用于执行机构。

1.2 模糊神经网络控制原理

模糊神经网络是模糊控制和神经网络的结合[5]，既能够根据模糊规则进行模糊逻辑推理，又能够对非线性系统有很好的逼近能力[6]，兼顾了模糊控制和神经网络的优点。模糊神经网络PID控制系统包含模糊神经网络和PID控制器两部分[7]，采用模糊神经网络对PID控制器的3个参数进行调整，从而实现被控对象的自适应控制。模糊神经网络PID控制器的控制原理如图2所示。

图2 模糊神经网络PID控制器原理图

2 模糊神经网络设计

模糊神经网络PID控制系统将土壤湿度的测量值和设定值的偏差e、偏差变化率ec作为系统的两个输入变量，然后输出PID控制器的3个系数KP、KI、KD。将这5个变量分别量化为7个等级，即为{NB、NM、NS、Z、PS、PM、PB}，量化论域都为{-6，-4，-2，0，2，4，6}。e和ec的模糊子集均为7个，模糊推理采用Mamdani推理[8]，模糊规则可表示为：ife=Aandec=BthenKP=CandKI=DandKD=E，共有49条模糊规则[9]，具体如表1所示。

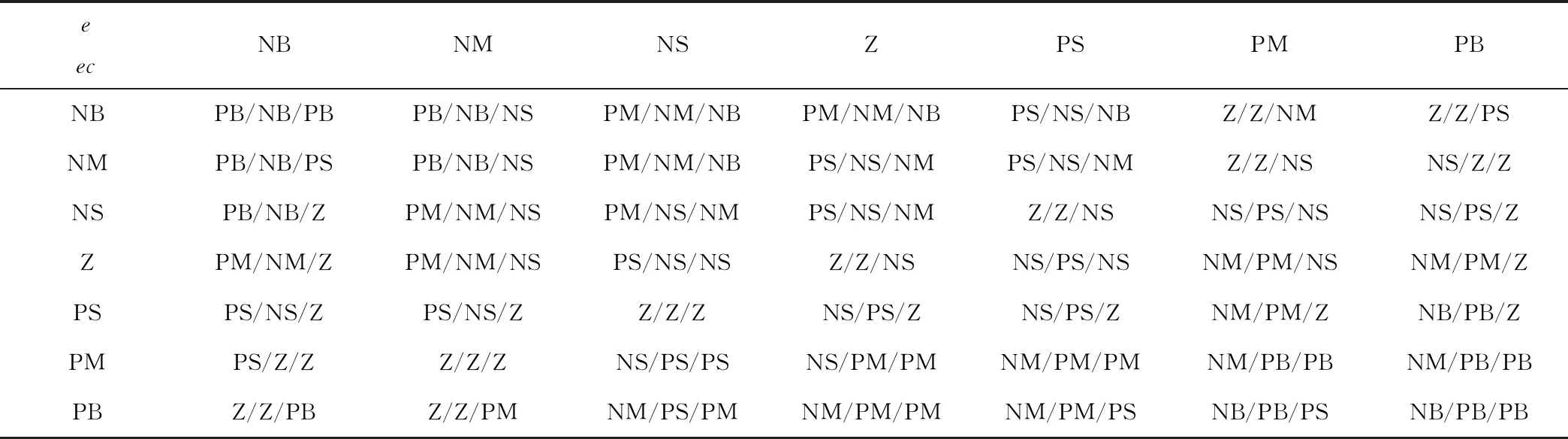
表1 模糊控制规则表

基于Mamdani的神经网络模型如图3所示，采用5层全连接的BP神经网络[10]，神经网络结构如图3所示。偏差e和偏差变化率ec作为模糊神经网络的两个输入神经元，PID控制器的3个参数KP、KI、KD作为模糊神经网络的3个输出神经元[11]，神经网络拓扑结构为2-14-49-7-3。

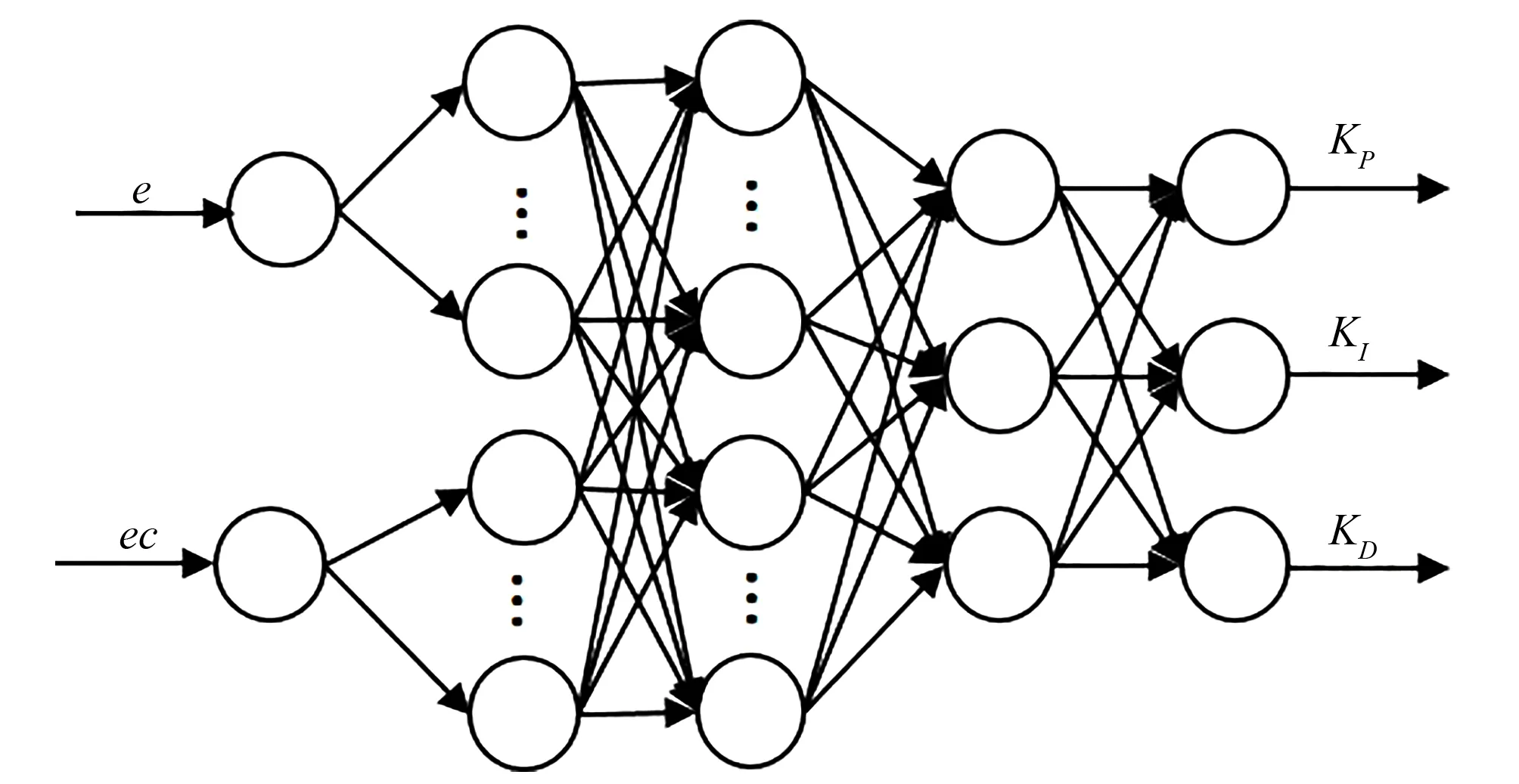
图3 模糊神经网络

网络学习算法如下：

(1)正向传播。任意一个隐含层神经元的输入是前一层所有神经元的加权输出值，即：

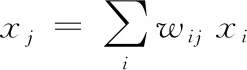
(4)

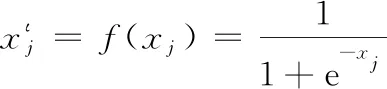
(5)

则：

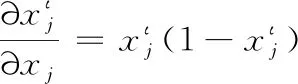
(6)

输出层神经元的输出为：

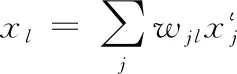
(7)

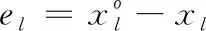
(8)

第p个样本的误差性能指标函数为：

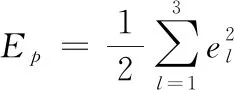
(9)

其中，3为输出层神经元的个数。

(2)反向传播。采用有动量的梯度下降法，调整各层间的权值。权值的更新算法如下：

输出层及隐含层的连接权值wjl更新算法为：

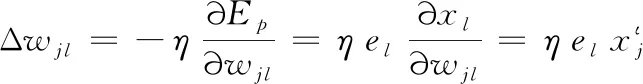
(10)

其中，η为学习速率，η∈[0,1]。

k+1时刻网络的权值为：

wjl(k+1)=wjl(k)+Δwjl

(11)

隐含层和输入层连接权值wij学习算法为：

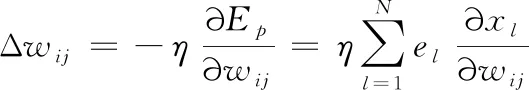
(12)

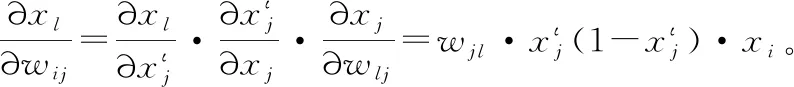
k+1时刻网络的权值为：

wij(k+1)=wij(k)+Δwij

(13)

考虑上一次权值对本次权值变化的影响，需要加入动量因子α，此时的权值为：

wjl(k+1)=wjl(k)+Δwjl+α[wjl(k)-wjl(k-1)]

(14)

wij(k+1)=wij(k)+Δwij+α[wij(k)-wij(k-1)]

(15)

其中，α为动量因子，α∈[0,1]。

神经网络的正向传播计算输出层误差，反向传播调整各层权值，一次正反向传播就完成一次迭代，经过多次迭代后，误差越来越小，就可以得到所需的网络训练模型，根据网络学习算法得到模糊神经网络的训练流程如图4所示。

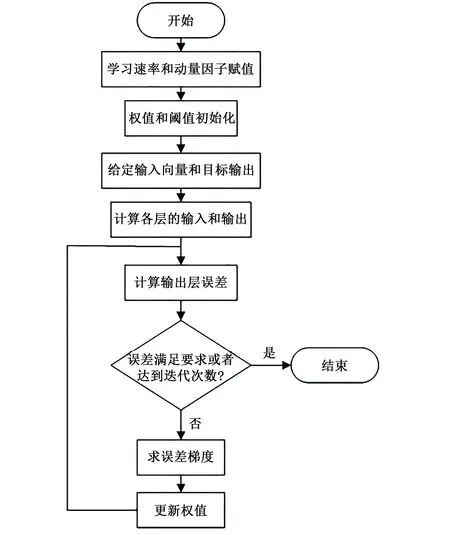
图4 模糊神经网络流程图

根据模糊神经网络流程图，在MATLAB中编写模糊神经网络算法，网络动量因子和学习速率分别设为 和 ，设定网络最大训练次数为7 000 次，目标误差为0.01，然后进行神经网络离线训练，将离线训练好的神经网络转换为Simulink仿真模块，如图5所示。

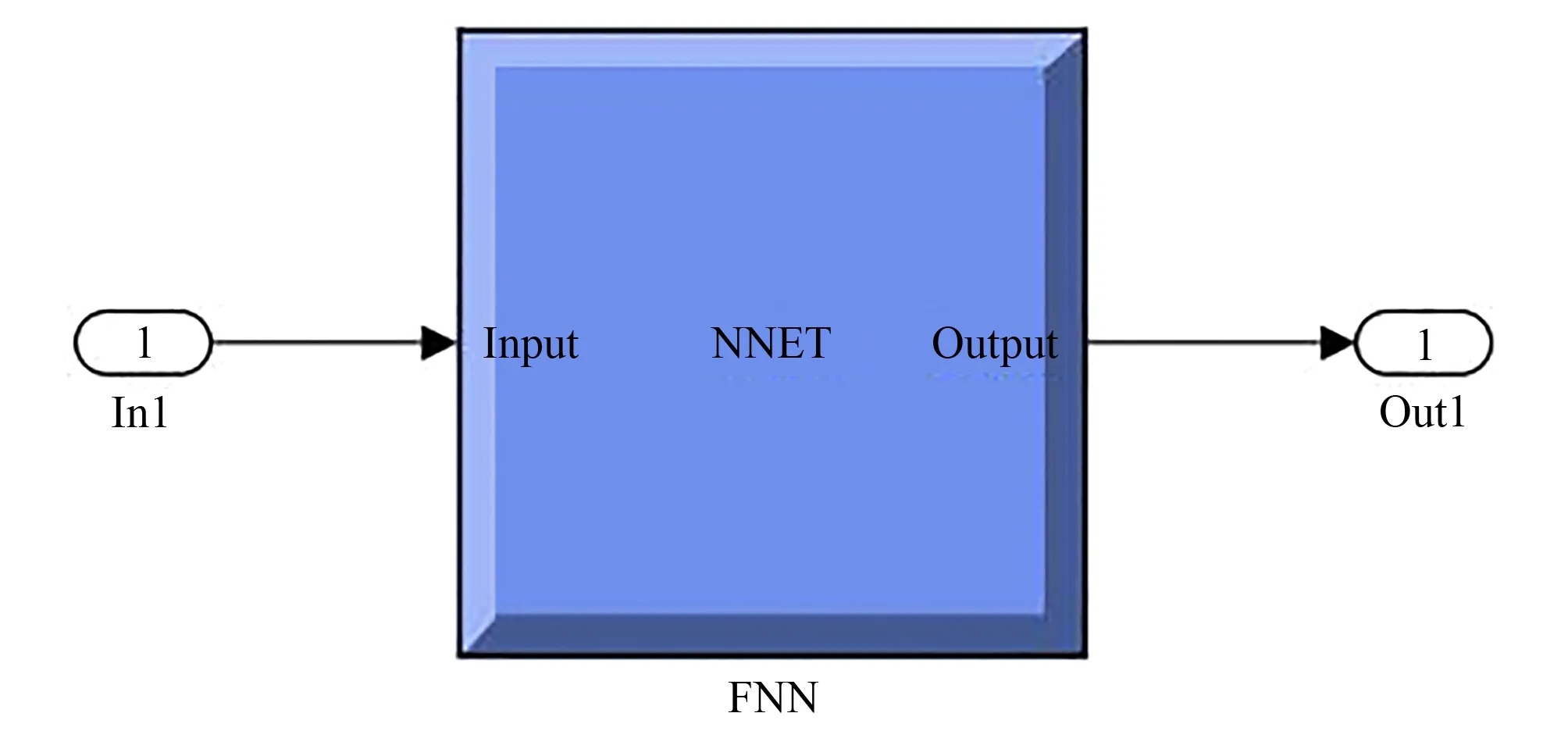
图5 模糊神经网络Simulink仿真模块

3 模糊神经网络控制仿真与分析

枸杞在不同的生理周期对土壤湿度的要求不同，表2为枸杞对土壤湿度的要求。本系统只对枸杞展叶期最佳土壤湿度15%进行算法仿真设计，其他生理周期同理。

表2 枸杞生长周期

根据滴灌经验，滴灌过程可以近似看作一个具有非线性和时滞的一阶系统[12]，其传递函数可表示为：

(16)

取各参数为：k=0.023，τ=27，T=800，本文将结合建立的枸杞滴灌数学模型，在MATLAB中使用Simulink搭建仿真模型[13]，进行仿真实验。

根据经验法进行多次PID参数整定，最终确定KP、KI、KD的值为100、0.4、0.1。分别搭建PID仿真模型和模糊神经网络PID仿真模型[14]，PID仿真模型如图6所示，模糊神经网络PID仿真模型如图7所示。

3.1 阶跃干扰下仿真

在Simulink中建立仿真模型，并且分别给PID控制系统，模糊神经网络PID控制系统一个单位阶跃信号[15]，待系统进入稳态后，在PID控制系统仿真模型和模糊神经网络PID控制系统仿真模型 处放置阶跃干扰，仿真结果如图8所示。

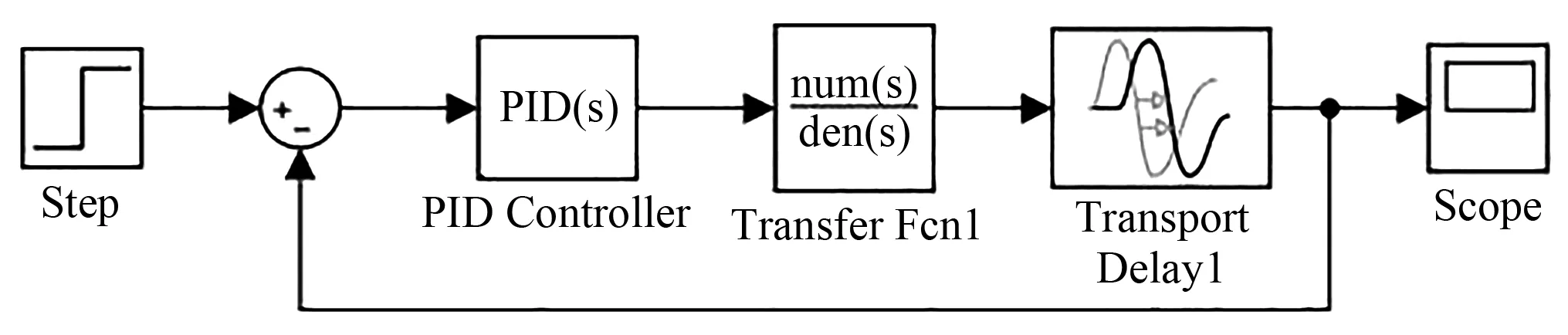
图6 PID仿真模型

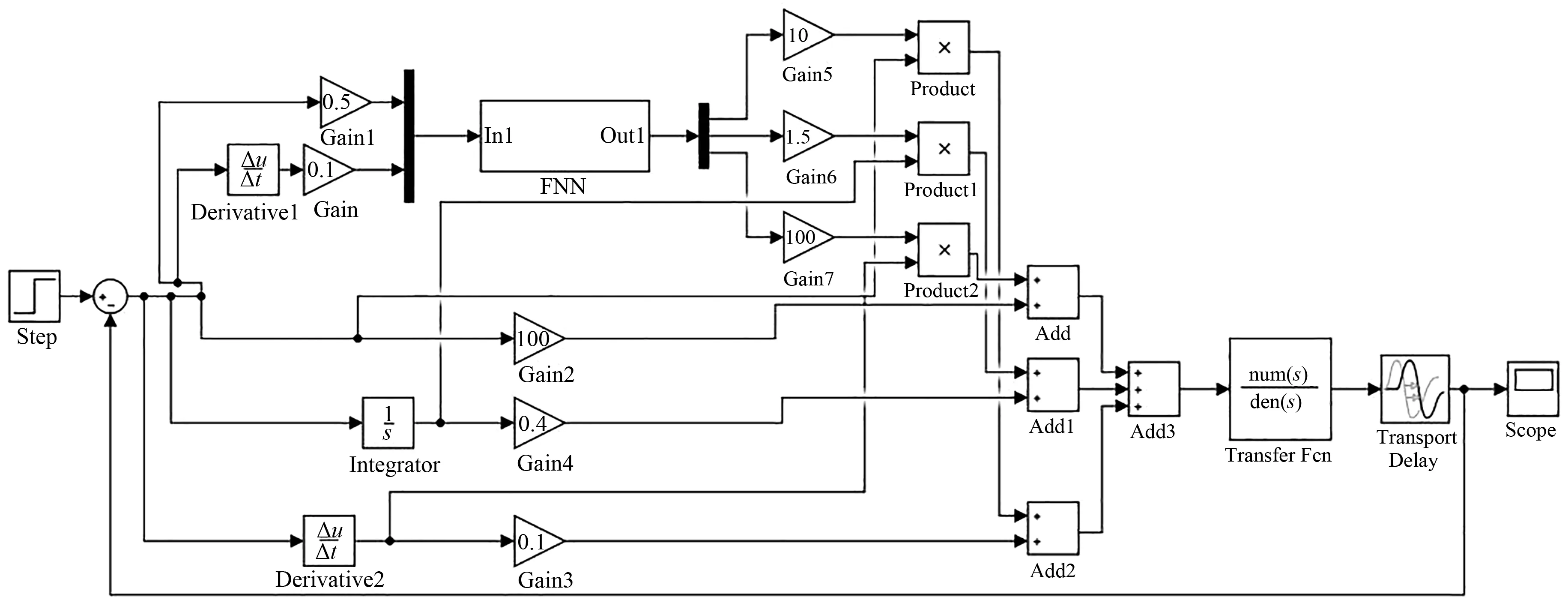
图7 模糊神经网络PID仿真模型

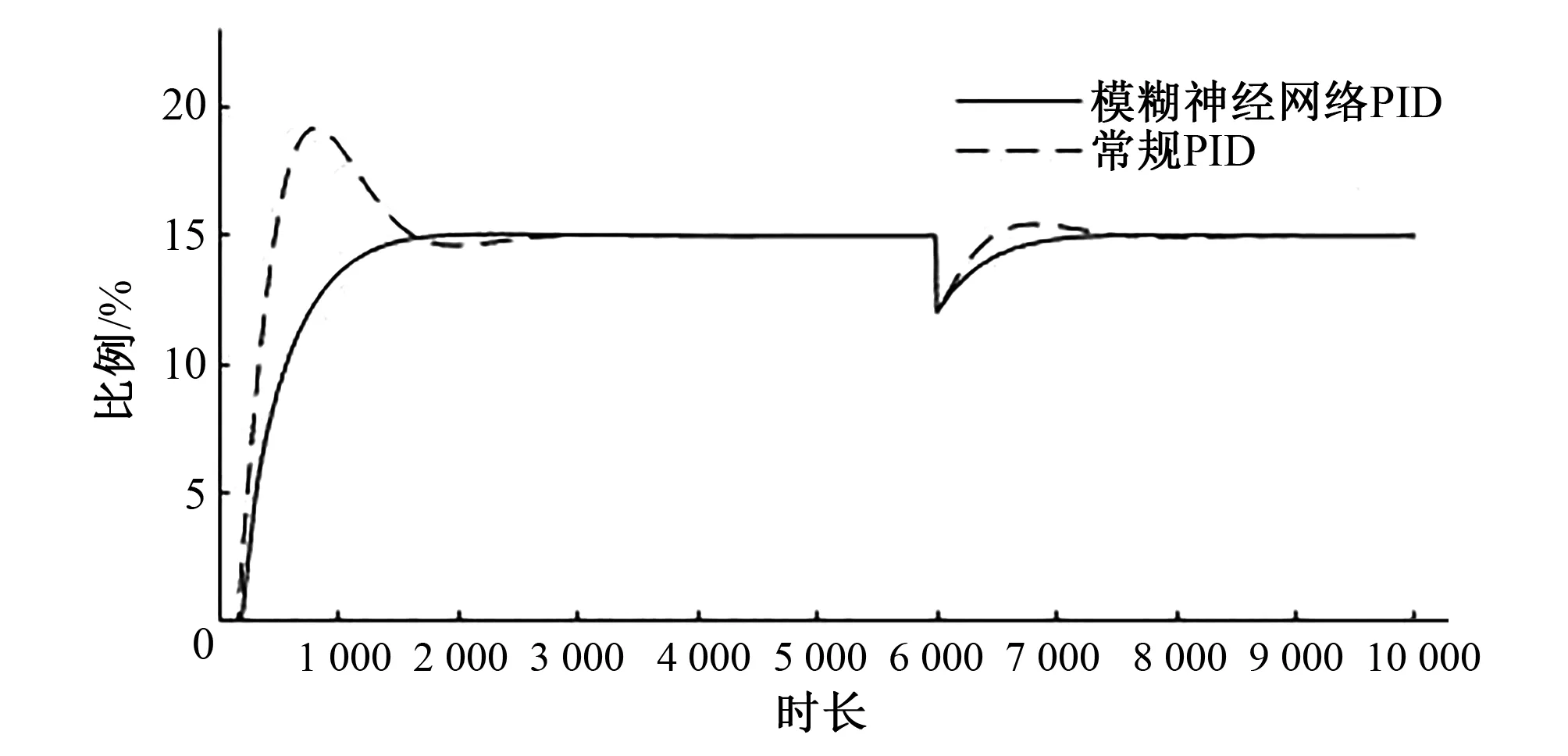
图8 阶跃干扰下的控制仿真图

从图8中可以看到模糊神经网络PID控制效果比PID控制效果好[16]，能够将枸杞生长所需要的最佳土壤湿度控制在15%，并且调节时间短，超调量小，响应速度快。在经过一个阶跃干扰后，模糊神经网络PID能够迅速达到稳态，说明模糊神经网络PID控制具有更强的自适应能力和抗干扰能力。

3.2 模型失配下仿真

在实际的灌溉系统中，被控对象会受到风速，温度等因素影响，导致模型的参数产生变化，所以要求控制系统具有自适应能力，能够根据系统工况变化做出反应。为了模拟实际控制系统，需要在一定范围内修改传递函数的时间常数、开环增益等。在此，将时间常数改为1 200，利用建立的模型进行仿真，仿真曲线如图9所示。

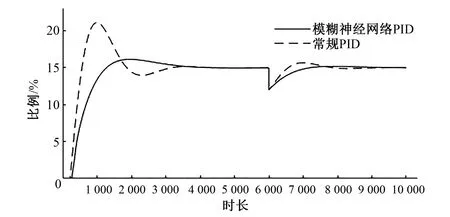
图9 模型失配下的控制仿真图

从图9中可以看到，当被控对象的数学模型变化时，两种输出曲线都发生了变化，常规PID控制的输出曲线震荡较之前明显，模糊神经网络PID控制输出曲线震荡较小，说明了当模型失配时，模糊神经网络PID控制器能快速应对干扰，迅速达到稳定状态。

4 结 论

枸杞滴灌是一个非线性、实时变化的过程，本文设计了一种模糊神经网络PID控制系统对枸杞滴灌进行控制，并在Simulink中进行仿真分析，从仿真曲线中可以看出其超调量小，系统稳定性强，比传统的PID控制效果好，在枸杞滴灌中具有很好的应用前景。