基于奇异值分解的稀疏信道估计
陈发堂 侯宁宁 范艺芳
(重庆邮电大学通信与信息工程学院 重庆 400065)
0 引 言
正交频分复用(Orthogonal Frequency Division Multiplexing,OFDM)技术与多输入多输出(Multi Input Multi Output,MIMO)技术两者相结合,不仅有效提高了无线系统的通信质量,同时还提高了系统容量。但受无线信道环境的制约,信号在传输过程中会受到不同程度的衰落和延时,从而引发符号间的干扰(Inter Symbol Interference,ISI)[1]。为了有效降低ISI,提高信号的传输质量,必须对信道状态信息(Channel State Information,CSI)进行精确估计,可见信道估计在无线通信系统中颇为重要。
传统估计方法,如最为常用的最小二乘(Least Squares,LS)算法以及最小均方误差(Minimum Mean Square Error,MMSE)算法,在信道估计时都需要采用大量的导频信号。考虑到导频信号不含任何有价值的信息,但在传输过程中依然占用频带资源,因此传统估计方法对频带资源的占用颇为严重,致使频带资源利用效率低。2006年,Donoho等提出了压缩感知(Compressed Sensing,CS)理论,该理论表明借助信号的稀疏特性,只需要少量的观测值就可以高效率地恢复出原始信号[2-3]。同时,文献[4]表明无线多径信道具备稀疏特性。因此,可以充分利用无线多径信道具备稀疏性这一特点,将压缩感知理论与信道估计相结合,在提高频带资源利用率的基础上获得较好的估计效果。
以CS为依据,文献[5]采用匹配跟踪(Matching Pursuit,MP)算法以及文献[6]采用正交的匹配跟踪(Orthogonal Matching Pursuit,OMP)算法进行了信道估计,同时验证了压缩感知理论在信道估计中的有效性。为了降低噪声的影响,在OMP算法基础上,Needell等[7]提出了一种新的具有抗噪能力的压缩采样匹配跟踪(Compression Sampling Matching Pursuit,CoSaMP)算法。但以上三种算法都存在相同的问题,即必须预先已知信道的稀疏度,而在实际应用中,信道的稀疏度很难获取,因此又提出了一种稀疏自适应的匹配跟踪(Sparsity Adaptive Matching Pursuit,SAMP)算法[8]。SAMP虽然解决了算法过度依赖信道稀疏度的问题,但其算法的性能和复杂度不能达到折中,即无法同时兼顾,也就是说性能好时复杂度高,复杂度低时性能不佳。此外,算法的抗噪能力也相对较差,有待进一步优化和提升。
为了进一步优化算法的估计精度,同时减小算法的复杂度,本文提出了一种新的具有抗噪能力且稀疏度自适应的压缩感知估计算法,并称之为N-SAMP算法。该算法在不需要事先知道信道稀疏度的前提下,采用自适应步长来提高算法的重构效率;迭代过程中,与奇异值分解技术相结合,并根据奇异熵来确定有效的重构阶次,达到过滤相关性较小原子的目的,同时,还起到了抵抗噪声干扰的作用。仿真结果表明,N-SAMP算法与传统重构算法相比,估计精度得到了明显提升,尤其在信噪比较低的信道环境下,与此同时,重构效率也得到了进一步的改善。
1 系统模型
MIMO-OFDM系统模型如图1所示。

图1 MIMO-OFDM系统模型
在MIMO-OFDM系统的发送端,传输的信号首先需要进行快速的傅里叶逆变换(Inverse Fast Fourier Transform,IFFT),然后再加循环前缀(Cyclic Prefix,CP)。加CP时,为避免载波间以及符号间的干扰,其所加CP的长度需要大于最大的时延路径,最后进行并串变换处理。在MIMO-OFDM系统的接收端,也就是对发送端进行一个逆过程处理,即依次进行串并变换、去CP以及FFT变换。假如MIMO-OFDM系统的发送天线的个数为NT,接收天线的个数为NR,子载波个数为K,且保证一个OFDM符号内的信道参数完全一致,则该系统模型可表示为:
(1)
式中:zn(k)表示接收天线n在第k个子载波上的加性高斯白噪声(Additive White Gaussian Noise,AWGN);sm(k)表示发送天线m在第k个子载波上所发送的信息;rn(k)表示接收天线n在第k个子载波上所接收到的信息;Hnm(k)表示发送天线m与接收天线n在第k个子载波上的冲激响应。Hnm(k)的表达式为:
(2)
且有:
(3)
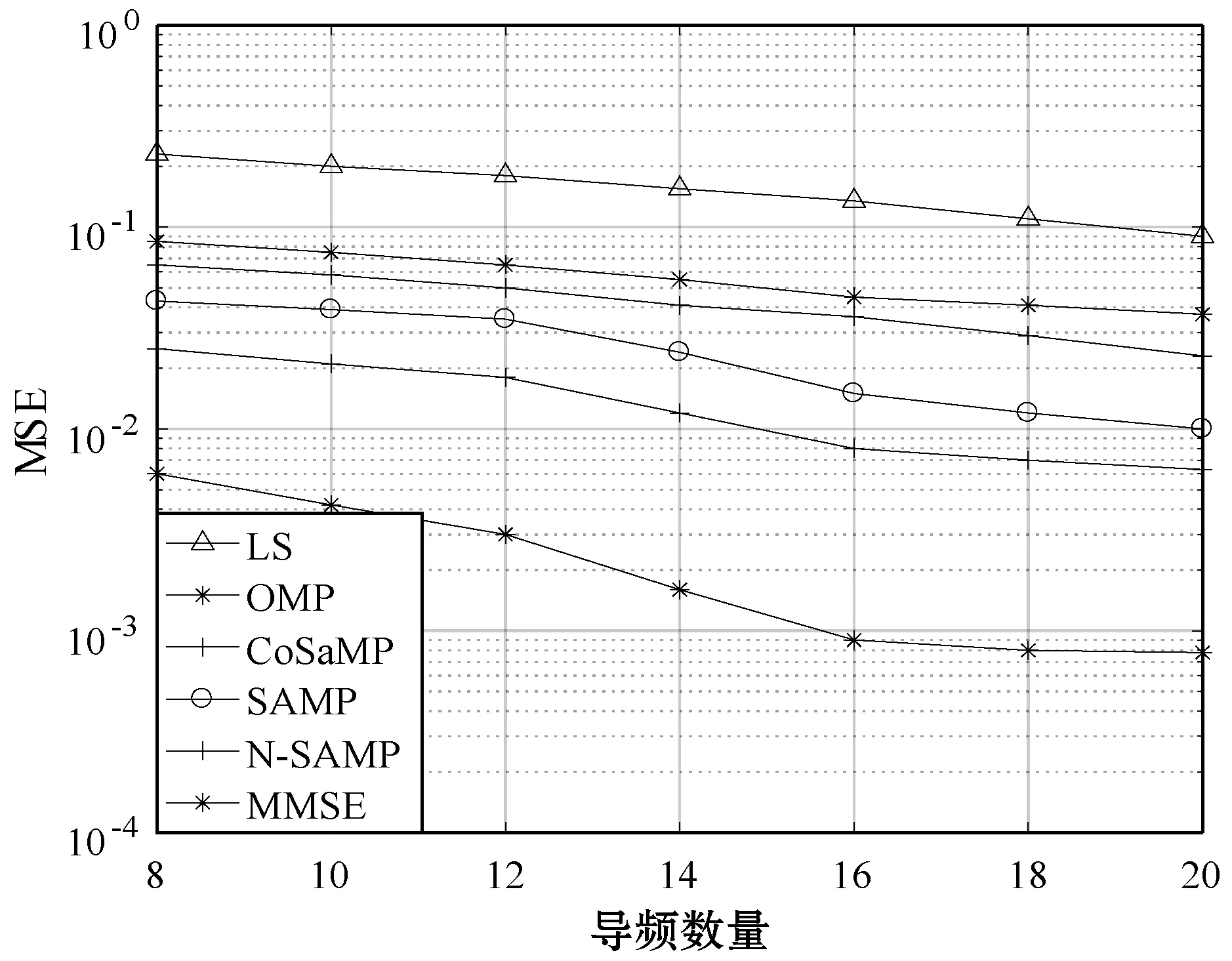
式中:L代表信道的多径个数;αnm代表发送天线m与接收天线n之间的增益;τj代表发送天线m与接收天线n在第j个路径上的时延。令hnm=[hnm(0),hnm(1),…,hnm(L-1)]T,实际通信环境中,hnm是由少量多径延迟抽头系数组成,也就是说,若hnm中非零元素的个数用T来表示,则满足T< MIMO-OFDM无线通信系统中,假如有W个导频信号,且依次位于k1、k2、…、kW子载波上,则接收天线n所接收到的导频信息可表示如下: (4) 式中:rn=[rn(k1),rn(k2),…,rn(kw)]T表示接收天线n所接收到的导频信息,sm=[sm(k1),sm(k2),…,sm(kw)]T表示发送天线m所发送的导频信息,zn=[zn(k1),zn(k2),…,zn(kw)]T表示接收天线n上的加性高斯白噪声,Fs∈RW×L为离散的傅里叶变换阵F且维度为W×L的一个子矩阵。F的表达式如下: (5) 接收到的信号可进一步表示如下: R=SFsh+z (6) 压缩感知理论表明:若信号本身是具有稀疏性的或者是在某个变换基下具有稀疏性,用少量的观测值就能有效地恢复出原始信号。其数学模型如下: y=Φx+z=ΦΨα+z=Θα+z (7) 式中:y∈RM代表观测向量;z∈RM代表噪声矢量;Ψ∈RN×N表示变换基;x∈RN,若x稀疏,Φ表示M×N维观测矩阵且满足M< (8) 由于M×N维矩阵Φ或Θ满足M< 本文以压缩感知理论为依据,借鉴传统重构算法的处理流程,所提N-SAMP算法主要包括原子预选、预估计、基于奇异值分解的降噪处理以及原子裁剪四个阶段,具体见算法1。由式(6)以及算法流程可知,R∈RWNR相当于式(7)中的观测向量y,B=SFs相当于式(7)中的测量矩阵Φ。 算法1 N-SAMP算法流程 输入:观测向量R,测量矩阵B=SFs,参数α,β,ε 对于1≤t≤WNR, 1: 原子预选:计算残差与测量矩阵相关系数的绝对值,将大于阈值γ所对应B的序列号j构成集合J0; 2: 更新索引集:Δt=Δt-1∪J0 4: 通过(12)式计算Ek并使其满足Ek≥β,确定阶次k 6: 更新索引(原子裁剪):Δt=supp(Δt,k) 以向量x=[x1,x2,…,xn]和y=[y1,y2,…,yn]为例,首先向量进行标准化处理: (9) (10) (11) 式中:(·)†表示矩阵的伪逆过程;(·)-1表示矩阵的求逆过程;Δt=Δt-1∪J0,J0表示相关系数大于阈值γ所对应B的序列号j构成的集合。 (12) (13) 由式(13)计算奇异熵: (14) 式中:k表示奇异熵阶次。 在噪声过高的信道状态下,对角阵ΛP×P含有的非零元素较多,因此只保留对角阵ΛP×P中前k个元素,其余元素均设为零值,则式(12)可表示为: (15) 由表1的处理流程可知,本文算法在迭代过程中引入了α、β、ε三个参数。其中:α的大小决定了原子预选的个数,也就是步长D;β的大小决定了降噪阶次k的值;ε的大小决定了算法的迭代次数以及算法的复杂度。考虑到参数的取值大小会直接严重影响整体算法的性能,因此本文对以上参数进行了多次测试。基于大量的实验分析,当α取值在0.6到1之间,β取值在0.97到0.99之间,ε取值在0.1到0.5之间时,算法性能较为稳定,因此算法仿真时,α、β、ε三个参数的取值均在以上范围内。 为验证N-SAMP算法的估计效果以及对比所提算法与传统算法的性能差异,本文采用MATLAB软件进行搭建仿真链路,并利用均方误差(Mean Square Error,MSE)来加以衡量,均方误差定义如下: (16) 由式(16)可知,MSE值越小,表明估计精度越高。表1为MATLAB仿真参数。 表1 仿真参数 首先,图2对比了传统估计算法LS和MMSE以及基于压缩感知的OMP、CoSaMP、SAMP和本文所提N-SAMP算法的均方误差性能。通过观察图2可知,以上五种算法均方误差曲线整体保持一致,即都随信噪比的增加呈现出下降的趋势。此外,相同信噪比的前提条件下,N-SAMP算法的均方误差要小于LS、OMP以及CoSaMP。更值得一提的是,在信噪比较低的信道状况下,N-SAMP算法相较SAMP来说,性能更佳且更为稳定,如信噪比为5 dB时,N-SAMP算法的均方误差仅为SAMP的5%左右,约降低了95%,性能得到了极大提升。 图2 不同算法MSE曲线对比图 图3对比了传统估计算法LS、MMSE以及基于压缩感知的OMP、CoSaMP、SAMP和本文所提N-SAMP算法均方误差性能与导频数量间的关系,其中信噪比(Signal to Noise Ratio,SNR)取值在15 dB。通过观察图3可知,以上算法均方误差曲线整体上呈现出一个下降趋势,即均方误差都随着导频数目的增加而减小,也就是说算法的性能会随导频的增加而逐渐变好,这是因为导频个数的增加,说明观测向量所包含的原始信息就越多,因此误差就会变小。另外,当采用相同导频时,N-SAMP的均方误差要小于其他三种传统的重构算法;当均方误差相同时,N-SAMP所需的导频数量同样要低于其他三种传统的重构算法,这就说明本文所提N-SAMP算法能在采用较少导频的基础上取得比传统重构算法更佳的估计精度,同时还说明了N-SAMP能减少导频的开销,从而提高系统频谱资源的利用效率。 图3 不同导频MSE曲线对比图 为了比较各算法的计算复杂度,本文统计了基于压缩感知的SAMP、OMP、CoSaMP以及本文所提N-SAMP算法的运行时间,如图4所示。此外,为了更好体现所提算法具有较高的重构精度,对图4进行了数字化处理,如表2-表4所示。通过观察图4可以看出,以上四种算法的运行时间随信噪比的增加均呈现出下降趋势,即算法的运行效率随信噪比的增加而得到提高。在相同信噪比下,N-SAMP算法的运行时间要明显低于OMP、CoSaMP以及SAMP三种传统的重构算法。由表2-表4可以看出,相同信噪比下,N-SAMP算法运行时间相比SAMP降低了约15%,相比CoSaMP降低了约40%,相比OMP降低了约50%。 图4 各算法运行时间对比 表2 N-SAMP与SAMP运行时间对比 表3 N-SAMP与CoSaMP运行时间对比 表4 N-SAMP与OMP运行时间对比 本文鉴于基于压缩感知的估计方法能高效获得信道状态信息,提出了一种新的具有抗噪能力的基于压缩感知的N-SAMP估计算法,并将其应用到MIMO-OFDM无线通信系统。N-SAMP采用自适应步长来提高算法的重构效率,与奇异值分解技术相结合,并根据奇异熵来确定有效的重构阶次,进而过滤掉能量较低的原子,从而避免迭代过程中选取不太相关的原子,同时还抵抗了噪声的干扰,提高了算法的鲁棒性。与传统的重构算法相比,N-SAMP算法具有较好的估计效果,尤其在信噪比相对较低的信道状态下,性能更优且更加稳定,同时算法的复杂度还得到了进一步的改善。N-SAMP不需要事先知道信道稀疏度,具有较高的实用价值。
2 基于压缩感知的估计算法
2.1 压缩感知


2.2 基于N-SAMP的信道估计


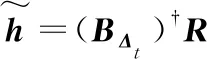




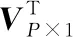

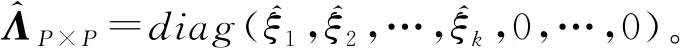

3 仿真结果及分析






4 结 语

