基于神经网络的换热站二次回水温度预测方法
董 晨 周浩杰 宫铭举* 王 晟 杨 鹏 赵 义
1(天津理工大学计算机科学与工程学院天津市智能计算及软件新技术重点实验室 天津 300384)
2(天津理工大学电气电子工程学院 天津 300384)
3(春华(天津)能源管理有限责任公司 天津 300202)
4(天津华春智慧能源科技发展有限公司 天津 300000)
0 引 言
集中供热系统是一种公用事业能源服务系统,不同于个别房屋的供暖,集中供热系统需要投资于整个区域的分销网络[1-2]。集中供热系统的合理调节和节能控制是一项跨学科、跨领域的综合技术,对提高热网的运行工况有着十分重要的意义[3]。
换热站是集中供热系统中非常重要的组成部分,它是连接锅炉与热用户之间的桥梁,具有至关重要的作用。换热站二次回水温度直接反映用户供热质量,由于集中供热系统的时变性、时滞性及非线性的特点,其换热站温度控制系统中的二次回水温度需要根据实际情况确定,因此根据实际工况,建立换热站二次回水温度预测模型显得尤为重要。在过去的几十年里,学者们提出了许多提高预测准确性的方法。传统基于统计的负荷预测方法包括线性回归[4]、自回归、移动平均、回归树、自回归整合移动平均模型[5]及其一系列变体[6]。这些统计模型仅在稳定的数据上表现良好,热负荷时间序列不可能是稳定的[7]。神经网络算法也广泛应用于二次回水温度的预测。文献[8]将一次供水温度、一次供水流量、二次供水温度、二次供水流量及室外温度作为输入,通过径向基函数(RBF)预测模型来预测二次回水温度。文献[9]通过基于回水温度平衡法的智能二网平衡系统来降低能耗。
本文根据实测的天津市文博园的换热站数据及天气情况数据,通过皮尔逊相关系数进行相关性分析建立三个预测特征集,分别构建了循环神经网络(RNN)、深度神经网络(DNNs)和长短期记忆网络(LSTM)三种神经网络预测模型,实现对二次回水温度的预测,并根据各个模型在不同预测特征集上的实验结果,挑选了最优的预测模型。
1 建立二次回水为温度预测特征集
采集到的气象数据包括室外温度、风力、相对湿度及空气质量(AQI),时间间隔为一小时;采集到的换热站数据间隔是一分钟,包括换热站一次网的供水温度、一次网的回水温度、二次网的供水温度及二次网的回水温度。通过计算各个温度参量在每个小时内的均值、最大值及最小值,构成换热站的数据。
集中供热系统中,换热站每个小时内的一次供水温度均值、一次供水温度最大值、一次供水温度最小值、一次回水温度均值、一次回水温度最大值、一次回水温度最小值、二次供水温度均值、二次供水温度最大值、二次供水温度最小值、室外温度、相对湿度、风力及空气质量,任意一条数据的变化都会引起二次回水温度的变化,然而,这些因素对二次回水温度影响程度各不相同,因此,采用皮尔逊系数来分析这些变量之间的相关性。
各影响因素与二次回水温度之间的皮尔逊系数r的计算公式如下:
(1)
各个影响因素与二次回水温度之间的皮尔逊系数r的值介于-1和1之间,即-1≤r≤1,且当0<|r|<1时,表示该变量与二次回水温度存在一定程度的线性相关。|r|越接近1,表示两变量间线性关系越密切;|r|越接近于0,表示两变量的线性相关越弱。
在特征选择时,各个影响因素与二次回水温度之间的皮尔逊相关系数如图1所示。

图1 皮尔逊相关系数示意图
图1为各个影响因素与二次回水温度的相关系数柱状图。可以看出,气象数据中的相对湿度和AQI与二次回水温度的相关性较小,因此,将相对湿度和AQI这两个参数剔除,并建立如下三个特征集来实现对二次回水温度进行预测,如表1所示。

表1 二次回水温度预测的特征集
Set1:只包含一次供水相关特征、室外温度及风力,在系统实际运行过程当中,工作人员通过控制一次网供水温度来调节集中供热系统,所以此特征集可以模拟集中供热系统实际运营状况。
Set2:包含除了室外温度之外的其他10个参数,可以探究室外温度对二次回水温度的影响。
Set3:包含所有参数,共11个特征。
2 二次网回水温度预测模型设计
根据相关性分析建立三个预测特征集,各个模型在特征集Set1、Set2和Set3的输入神经元个数分别为5、10和11,输出神经元个数为1。
2.1 RNN预测模型设计
RNN专门设计用于在顺序数据或时间序列上运行,建立的RNN模型隐含层包含40神经元,RNN的结构如图2所示。

图2 RNN结构图
给定一个输入时间序列x={x1,x2,…,xt},RNN使用式(2)、式(3)迭代地计算隐藏状态序列h={h1,h2,…,ht}以及输出序列y={y1,y2,…,yt}。
ht=f(Whxxt+Whhht-1+bh)
(2)
yt=g(Wyhht+by)
(3)
式中:Whx、WhhWyh表示权重矩阵;向量bh、by表示偏差;f(·)表示隐藏层的激活函数;g(·)表示输出层的激活函数。
2.2 DNNs预测模型设计
建立的DNNs模型由4层构成,如图3所示。

图3 DNNs结构图
第一层是输入层,第二层和第三层是隐藏层,分别有50和40个神经元,最后一层是输出层,只有一个神经元,这些层均采用ReLU激活函数。此外,为了克服过度拟合问题,在完全连接层中使用了Dropout[10],在某些训练迭代过程中,神经元随机死亡,即所选神经元的输出值等于零。
2.3 LSTM预测模型设计
建立的LSTM模型的两个隐含层神经元个数分别为50和100,LSTM的结构[11]如图4所示。

图4 LSTM网络结构图
LSTM的存储单元有三个门:输入门、遗忘门及输出门,单个LSTM单元的操作如下:
ft=σ(Wf·[[ht-1,xt]+bf)
(4)
it=σ(Wi·[ht-1,xt]+bi)
(5)
(6)
(7)
ot=σ(Wo·[ht-1,xt]+bo)
(8)
ht=ot×tanh(Ct)
(9)

3 二次回水温度预测流程
换热站二次回水温度预测流程为:(1) 将包括天气情况的数据和换热站一次网二次网数据的原始数据加载到存储器中;(2) 执行数据预处理,并且将数据归一化到[0,1]范围内;(3) 对数据进行特征相关性分析,通过相关性分析,确定二次回水温度预测的输入特征;(4) 根据特征相关性分析的结果建立3个预测特征集,将特征集划分为训练集、验证集和测试集;(5) 用训练集对预测模型进行训练,通过在交叉验证来优化参数并输出最优预测模型。最后在测试集上进行验证,测试集包含两天(48 h)的数据,并计算各个预测模型在不同特征集下的预测性能。
二次回水温度预测流程如图5所示。

图5 二次回水温度预测流程图
4 实 验
验证实验平台为Windows 10系统的计算机(i7-7700 16GB DDR4 120GSSD+1T GTX1070 8GB独显),所用编程语言为Python,采用天津市文博园2017年至2018年采暖期的换热站数据及该地区的气象数据。第一步,安装仿真软件PyCharm(x64),并导入需要的函数库:numpy,pandas,keras,matplotlib,math,sklearn,time,csv;第二步,通过pandas函数库中的read_csv函数加载原始数据文件,并使用numpy函数库中的corr函数对原始数据进行相关性分析,确定输入,同时构建三个预测特征集;第三步,按训练集、验证集、测试集为8∶1∶1的比例划分数据,并进行交叉验证,最终输出的最优模型为:三层RNN(隐含层包含40个神经元),四层构成DNNs(两个隐含层分别包含50和40个神经元),四层LSTM(两个隐含层神经元个数分别为50和100);第四步,用不同的预测模型(RNN、DNNs及LSTM)在测试集上进行模型性能测试,测试集为最后两天共48组的实测数据。在测试中,除了预测模型不同,其他可能影响预测精度的因素均保持一致(如:迭代步数设置为400,目标函数均为MSE,优化算法均采用rmsprop等)。
4.1 模型性能
为了更准确地评估预测模型的性能,使用了三种标准误差测量来对性能进行基准测试,即均方根误差(RMSE)、平均绝对百分比误差(MAPE)和平均百分比误差(MPE)来分析预测性能。RMSE、MAPE和MPE的计算公式如下:
(10)
(11)
(12)

4.2 实验结果和分析
在实验过程中,选择的测试集共包含48个小时的数据,RNN、DNNs及LSTM三种预测模型的预测结果分别如图6-图8所示。其中:横轴表示时间(h),纵轴表示二次回水温度(℃)。

图6 RNN预测结果

图7 DNNs预测结果

图8 LSTM预测结果
RNN模型的二次回水温度预测结果如图6所示,可以看出,RNN在数据集Set1、Set2和Set3上均能够实现对换热站二次回水温度的预测,但是RNN在数据集Set3上的预测效果比在Set1和Set2上的预测效果好。DNNs模型的二次回水温度预测结果如图7所示,可以看出,DNNs在数据集Set3上的预测效果比在Set1和Set2上的预测效果好。LSTM模型的二次回水温度预测结果如图8所示,可以看出,LSTM在数据集Set3上的预测效果比在Set1和Set2上的预测效果好,但是,与DNNs预测结果相似,在两个二次回水温度突变处的预测效果并不理想。因此,各个预测模型在数据集Set3上的预测效果最好。
详细实验结果如表2-表4所示。表2为各个预测模型在Set1上的性能指标;表3为各个预测模型在Set2上的性能指标;表4为各个预测模型在Set3上的性能指标,表中最后一列为各个预测模型的运行时间。
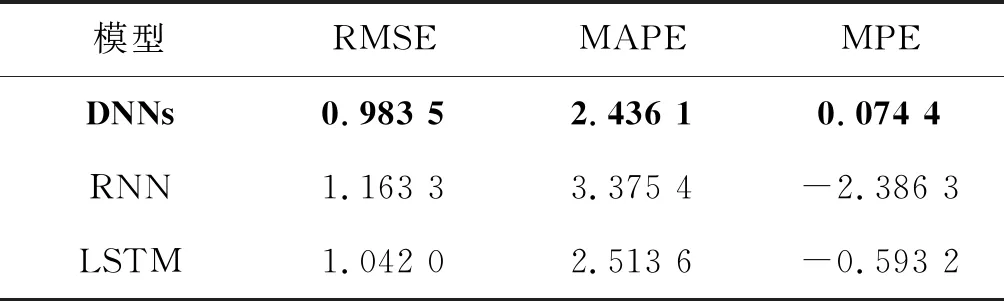
表2 各模型在Set1上的性能指标

表3 各模型在Set2上的性能指标

表4 各模型在Set3上的性能指标
数据集Set1仅包含一次供水相关特征、室外温度及风力共5个影响二次回水温度的特征。由表2可知,通过Set1中的特征能够实现预测二次回水温度,且DNNs模型能够更加准确地预测二次回水温度。因此,在对换热站的实际操控中,根据天气情况通过改变一次供水温度能够相应改变二次回水温度。
数据集Set3在Set2基础上同时考虑了室外温度。由表3可知,在数据集Set2上DNNs的预测效果最好。由表4可知,在数据集Set3上各个模型的MPE均为正值,其中RNN的预测效果最好、运行时间最短、运行效率最高。
MPE会告诉热网控制器的操作人员,具有正值的模型预测的二次回水温度没有超过实际值,而具有负值的模型将过度预测实际回水温度,从而造成能源浪费。因此,可以根据MPE相应地调整他们的操作。从表4中可知,各模型的MPE值均为正值,这表明模型预测的二次回水温度没有超过实际值,能够适当地节约能源。并且,在数据集Set3上采用RNN模型能够快速有效地预测二次回水温度并节约能源。
对比表3和表4的性能指标可知:在模型的输入中加入室外温度这一特征,能够提高预测性能,因此,在区域供热系统中,室外温度是影响二次回水温度变化的重要因素。
各个模型预测精度与降低的二次回水温度如表5所示。其中,最后一列为各个模型在数据集Set3上降低的二次回水温度总和。
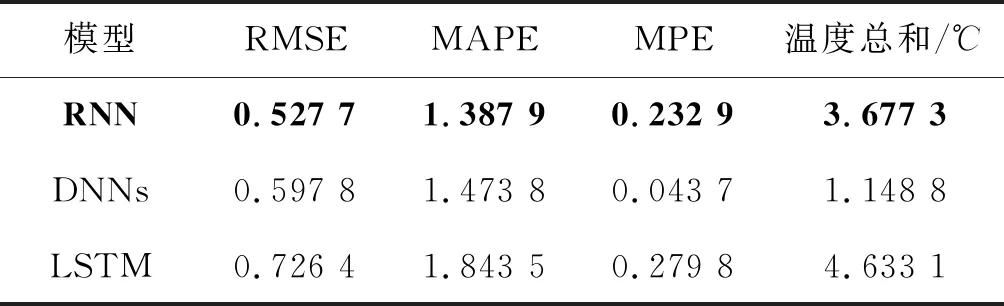
表5 各模型在Set3上降低的温度
从表5中可以看出,在数据集Set3上各个模型的MPE均为正值,MPE越大,降低的温度越多,节约的能源也越多。虽然LSTM降低的温度最多,为4.633 1℃,但是RMSE和MAPE误差较大,总体的预测结果不如RNN,而DNNs降低的温度为1.144 8℃,远小于RNN的3.677 3℃。因此,在数据集Set3上,RNN模型能够更加准确地预测二次回水温度,且二次回水温度降低了3.677 3℃,能够节约能源。
5 结 语
本文根据天津文博园实测的数据集,通过相关性分析建立三个预测特征集,分别构建RNN、DNNs和LSTM三种预测模型实现对换热站二次回水温度的预测。根据实验结果,有如下结论:(1) 在对换热站的实际操控中,根据天气情况通过改变一次供水温度能够相应改变二次回水温度;(2) 在集中供热系统中,影响换热站二次回水温度的主要气象因素是室外温度,空气质量和相对湿度对二次回水温度影响较小;(3)在数据集Set3上,采用RNN模型能够及时准确地预测二次回水温度,并且节约能源。

