基于短时PRI变换的多目标分选和识别算法
奚 银, 夏新凡, 吴迎春, 刘永杰, 王耀金
(上海无线电设备研究所,上海201109)
0 引言
反辐射雷达作为雷达电子战的重要组成部分,其主要功能是探测、截获和跟踪目标的辐射信号,并确定雷达参数。只有从随机交迭的信号流中分选出各个雷达信号的脉冲序列,才能进行雷达参数的测量、分析、识别和目标截获。雷达信号分选的基本原理就是分析截获信号的各种参数,将随机交迭的脉冲信号流自动分离成各部雷达的单独脉冲序列。用于雷达信号分选的主要参数有脉冲到达方向(DOA)、载频(RF)、脉宽(PW)、脉幅(PA)等。现有的信号分选方法都是在根据这些雷达参数进行预分选的基础上,再利用到达时间(TOA)进行脉冲序列的主分选,即脉冲重复间隔(PRI)分选,从而完成对目标的识别和截获。
针对电子战的发展趋势以及军方的作战需求,如何在复杂电磁环境下提升多目标分选及识别性能是反辐射雷达设计急需解决的关键问题之一。尤其是在反辐射雷达受到压制式干扰或虚假目标回波信号的欺骗式干扰时,传统的一维PRI分选已经难以满足反辐射雷达对多目标实时分选的要求,因此如何获取更全面的目标信息,提升反辐射雷达的目标检测性能成为研究的重点。
从上世纪80年代开始,各种PRI分选方法相继出现[1-5]。主要算法包括基于到达时间差(TDOA)直方图的算法[6-7]和变换域分析方法[7-15]。基于TDOA直方图的算法包括TDOA直方图算法、累积差值直方图(cumulative difference histogram,CDIF)算法、序列差值直方图(sequence difference histogram,SDIF)算法。这些算法都要计算脉冲序列的自相关函数,但由于周期信号的相关函数还是周期函数,在计算PRI时必然会出现子谐波现象,并且这些算法对PRI抖动和PRI正弦调制等复杂信号的分选能力较差。变换域类的PRI变换法以及修正的PRI变换法能够有效抑制谐波现象,还可以处理抖动PRI脉冲序列。该算法虽然能够分选抖动信号,估计出目标信号的PRI中心值,但无法描述和显示复杂调制PRI信号的变化规律。变换域分析法中的平面变换法[16-17],通过平面显示宽度的变换,能够将一维的脉冲到达信息转换成直观的二维图形,可以动态地显示PRI信息的调制规律,使分选变得直观。但平面变换后的特征曲线需要通过人工识别,并且一次调整只能给出一个目标的PRI信息,无法实现实时自动检测。
为了解决上述问题,本文提出一种短时PRI变换方法,在修正PRI变换的基础上,引入短时加窗的方法,对变换后的PRI谱图进行二维重排,获取目标的重频变化信息,有助于在进行目标分选识别的同时,实时获取PRI的短时特征信息。
1 PRI变换算法
1.1 基本原理
用脉冲前沿对应的时间tn(n=0,1,…,N-1)来表示脉冲的到达时间,其中N是采样脉冲数。如果只考虑TOA参数,采样脉冲串可以模型化为单位冲激函数的和,即

对交迭脉冲串做自相关运算,将在PRI及其整数倍处出现峰值,即会出现子谐波,这给脉冲重复周期的估计以及随后的信号分选造成了很大的困难。但是PRI变换中相位因子exp(j2πt/τ)或exp(j2πtn/(tn-tm))的引入几乎可以完全抑制自相关函数中的子谐波。
PRI变换中引入相位因子后,对到达时间差值固定的脉冲序列有较好的分选效果。对于抖动和其他复杂调制的PRI脉冲序列,落入同一PRI箱的脉冲的TOA差值不具有稳定的相位关系,使得真实的PRI值难以被准确地检测出来;另外随着TOA远离时间起点,PRI变换中相位因子的相位误差不断累积增大,使得相位因子不再有抑制谐波的作用。
1.2 修正算法
为了实现PRI抖动等复杂调制脉冲序列的分选,修正的PRI变换算法[3]被提出。该算法主要有两个方面的改进:一是利用可变的时间起点来降低相位误差;二是利用交叠的PRI脉冲箱来减少真实PRI的分散。
(1)可变时间起点技术
为防止相位误差的积累,可以利用可变的时间起点来修正相位变化的影响。PRI变换计算脉冲序列的相位时,没必要全部使用同样的时间起点。图1为脉冲到达时间示意图,图中τ为相邻脉冲重复间隔。
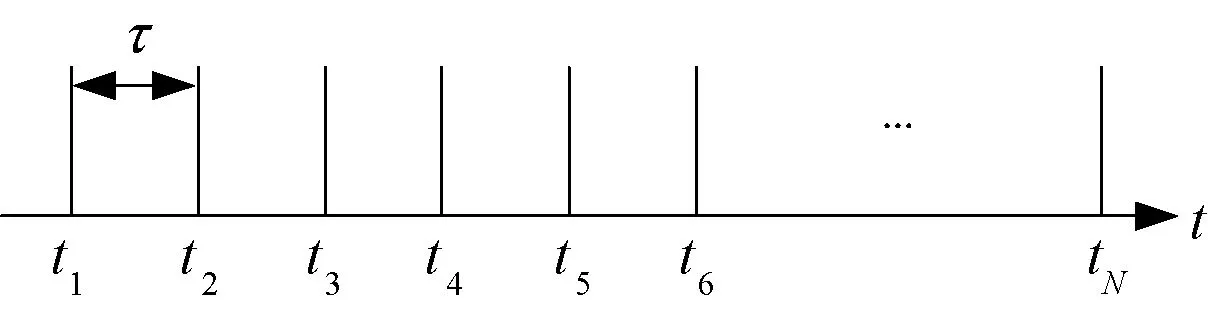
图1 脉冲到达时间示意图
脉冲对(t1,t4),(t2,t5),(t3,t6)的脉冲重复周期均为3τ,两两脉冲对PRI变换的相位因子表达式分别为
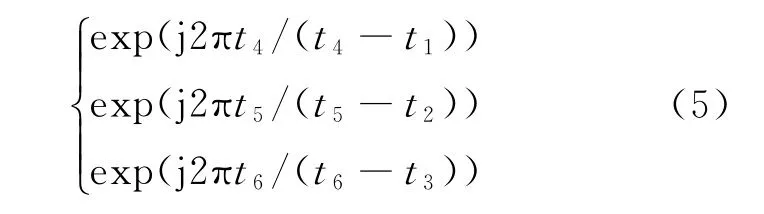
其中两两脉冲相位差表达式的分母均为3τ,分子分别为3τ,4τ,5τ。 这样3个相位加起来矢量和为0。但存在大的抖动的情况下,相位误差不断累积,使得矢量和不再为0,相位因子不再有抑制作用。为了减少相位误差的累积,在相位计算时不再以t1作为固定的时间起点,而是每隔k个脉冲改变一次时间起点。在存在脉冲丢失的情况下,当t m-o k与某个PRI箱中心值τk的整数倍接近时也要改变时间起点,其中t m为第m个脉冲的到达时间,o k为第k个PRI箱计算相位的时间起点。
可用如下方法改变时间起点。首先计算初始相位
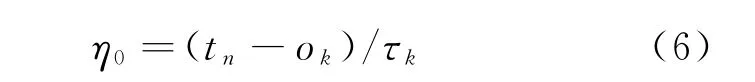
式中:t n为第n个脉冲的到达时间。这里,用τk代替t n-t m来缓和PRI抖动产生的影响。接着把相位分解为
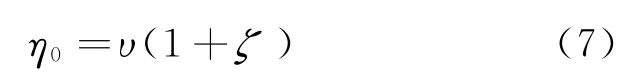
式中:υ为整数;ζ是(-0.5~+0.5)之间的实数。再根据以下3个条件来判断是否更新时间起点:
a)当υ=0时,不更新时间起点;
b)当υ=1时,若t m=o k,则使用t m作为新的时间起点;
c)当υ≥2时,若,则使用t n作为新的时间起点,其中ζ0为正的经验参数。
(2)交叠脉冲箱技术
为了对重频抖动目标进行分选,引入了交叠脉冲箱[4]的概念。设δ是PRI抖动上限,K为统计脉冲箱的个数,根据需求确定PRI的研究统计范围为[τmin,τmax],其中τmin和τmax分别为脉冲重复间隔的最大值和最小值。若τk为第k个PRI箱的中心值,则第k个脉冲箱的宽度b k的表达式为
式中:b=(τmax-τmin)/K。δ可以根据先验知识获得,PRI变换的门限设定准则详见文献[8]。
修正的PRI变换算法对PRI抖动和其他复杂调制信号有较好的分选效果,能够准确估计出目标PRI中心值,但不能分辨和显示目标的PRI调制或者变化特性。
2 短时PRI变换算法
短时PRI变换的基本思想,来源于PRI变换的方法和短时加窗滤波的方法。给连续的采样脉冲TOA加分析窗,本文采用简单的矩形窗,对交错脉冲信号加窗的示意图如图2所示。
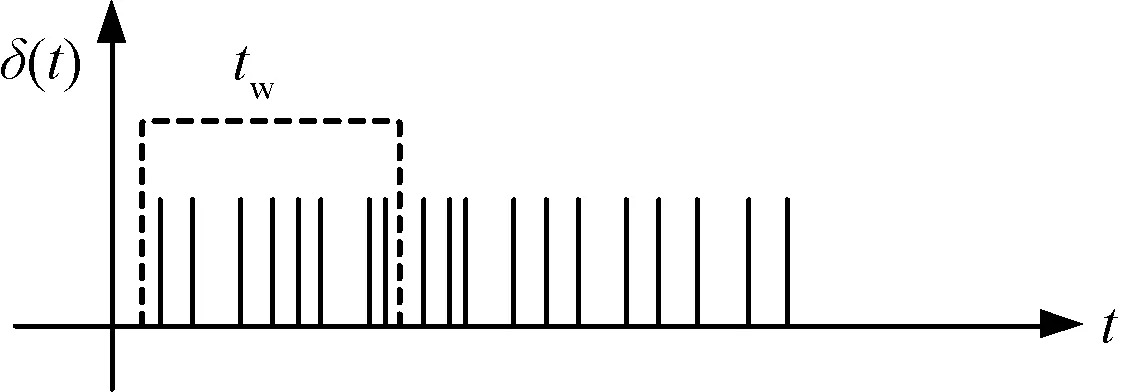
图2 信号加窗示意图
假设加窗函数长度为tw,加窗间隔为t i,则第k拍的短时PRI变换式为

将式(1)代入式(9),第k拍数据的离散PRI变换可表示为
式中:M为矩形窗内所包含的混合脉冲个数。根据第k拍的短时PRI变换谱图,可以获取当前时间段内目标的PRI信息。将各拍PRI谱图数据按照时间进行二维重排,如图3所示。横向为当前拍脉冲信号中目标PRI的估计和检测信息,纵向为目标PRI信息随时间的变化情况。因此二维的短时PRI变换谱图能获取多目标的PRI信息,并显示在不同时间段内的变化规律。
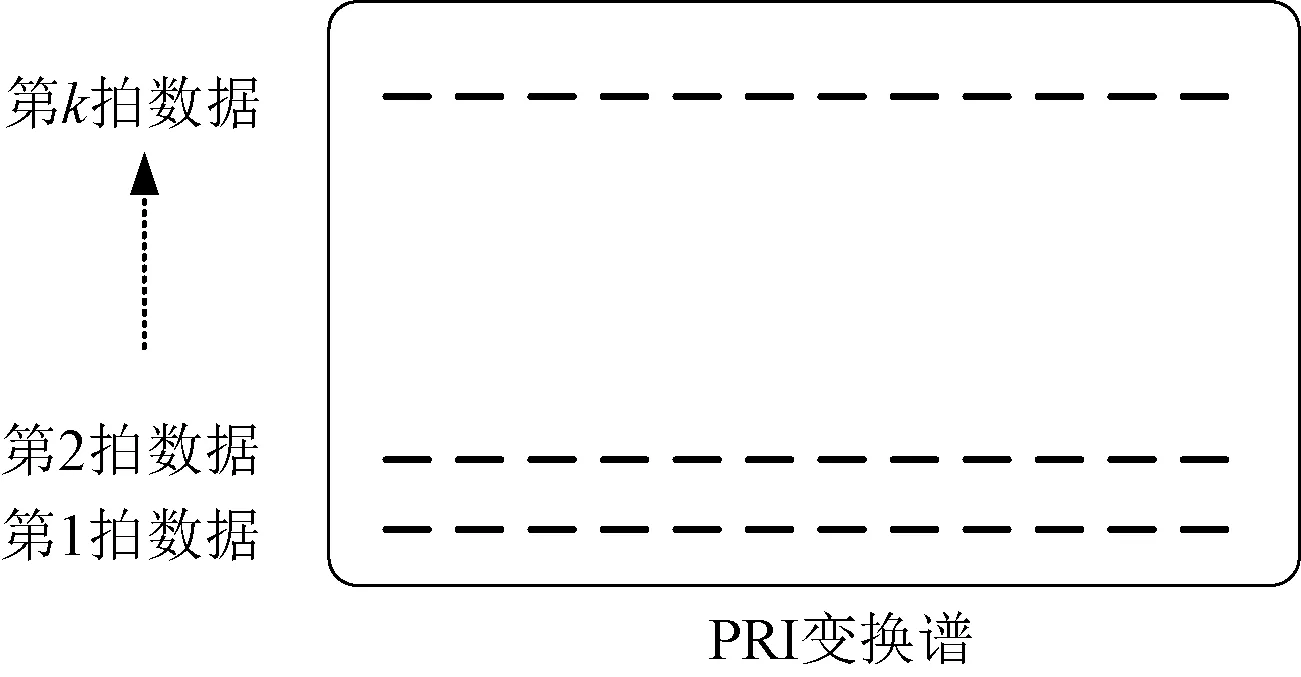
图3 短时PRI变换二维重排示意图
短时PRI变换算法将一维的脉冲TOA时域信息,变换为二维的时间-PRI变换域信息,实现了多目标PRI信息的实时平面显示,在进行目标分选识别的同时,可以实时观测和更新PRI随时间的变化信息。短时PRI变换算法的基本流程见图4。系统初始化后,选择合适的加窗宽度和加窗间隔;接收连续脉冲到达时间,并存入脉冲池内;计算当前窗口的起始时间和结束时间,当脉冲池中最大到达时间大于当前窗结束时间,则当前拍数据做短时PRI变换,否则继续等待脉冲;最终,将各拍PRI谱图数据按照时间进行二维重排,并更新二维短时PRI变换谱图。

图4 短时PRI变换算法的流程图
3 仿真分析
为验证短时PRI变换算法对多雷达目标信号的分选性能以及在实时平面显示方面的优势,选取3种典型的雷达脉冲信号,形成交错的目标脉冲流,采用短时PRI变换算法进行信号分选仿真试验,并与修正PRI变换算法进行对比。
仿真试验中,交错脉冲流包含一个固定重频信号、一个重频抖动信号(PRI抖动量5%)和一个重频正弦调制信号(调制度10%)。雷达脉冲信号参数如表1所示。
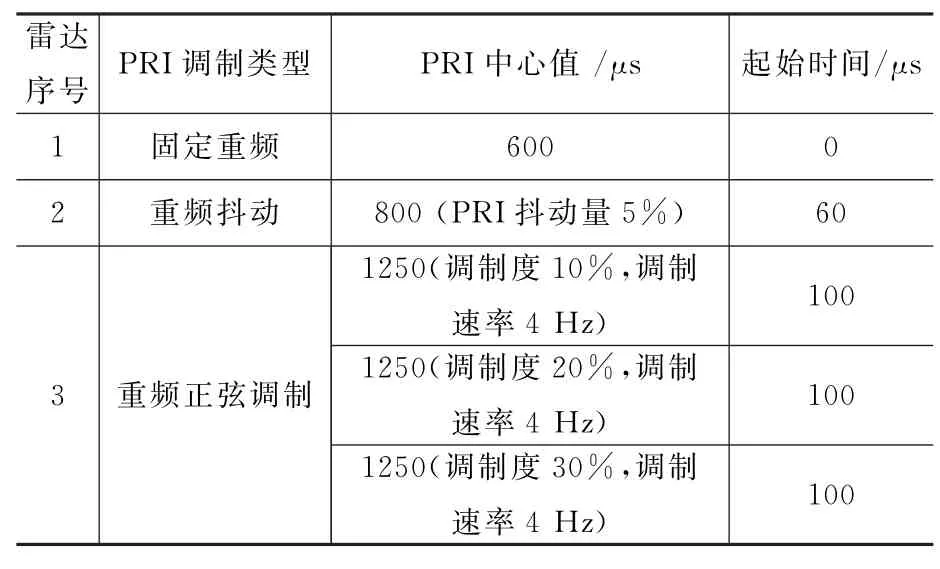
表1 雷达脉冲信号参数
设脉冲序列采样时长为300 ms,脉冲箱的个数为600,PRI范围为(0~2 000)μs,采用修正PRI变换法对交叠的脉冲流进行处理,重频正弦调制信号的调制度为10%时的PRI变换谱如图5所示,分别在600μs和800μs处出现谱峰。对于重频正弦调制信号的PRI变换谱,其谱峰有明显展宽现象,并在真实目标PRI处高于目标检测门限。可知,修正PRI变换算法能够分辨目标个数,但对于重频正弦调制信号,由于谱峰展宽,给准确估计目标的PRI中心值带来一定的难度,且无法获取目标PRI的调制规律信息。

图5 修正PRI变换谱图(调制度10%)
对上述交错脉冲流信号的TOA作短时PRI变换,以获取目标PRI的短时变化信息。其中,PRI脉冲箱的个数设置为600,采用矩形窗函数对数据进行加窗处理,单拍数据加窗时长为20 ms,窗的移动步进时长为6 ms。将获取的64拍脉冲数据做短时PRI变换并进行二维重排,谱图如图6所示。

图6 二维短时PRI变换谱图(正弦调制信号调制度10%)
可知,3个目标信号的PRI信息清晰显示在谱图中,在中心值600,800,1 250μs附近出现谱峰。对于正弦调制信号,对其短时PRI变换谱图进行峰值检索,获取目标PRI的正弦调制曲线,即可估计出目标PRI中心值。
为验证短时PRI变换算法对更大调制度PRI信号的分选性能,调制度分别设为20%和30%进行仿真,得到的二维短时PRI变换谱图如图7所示。
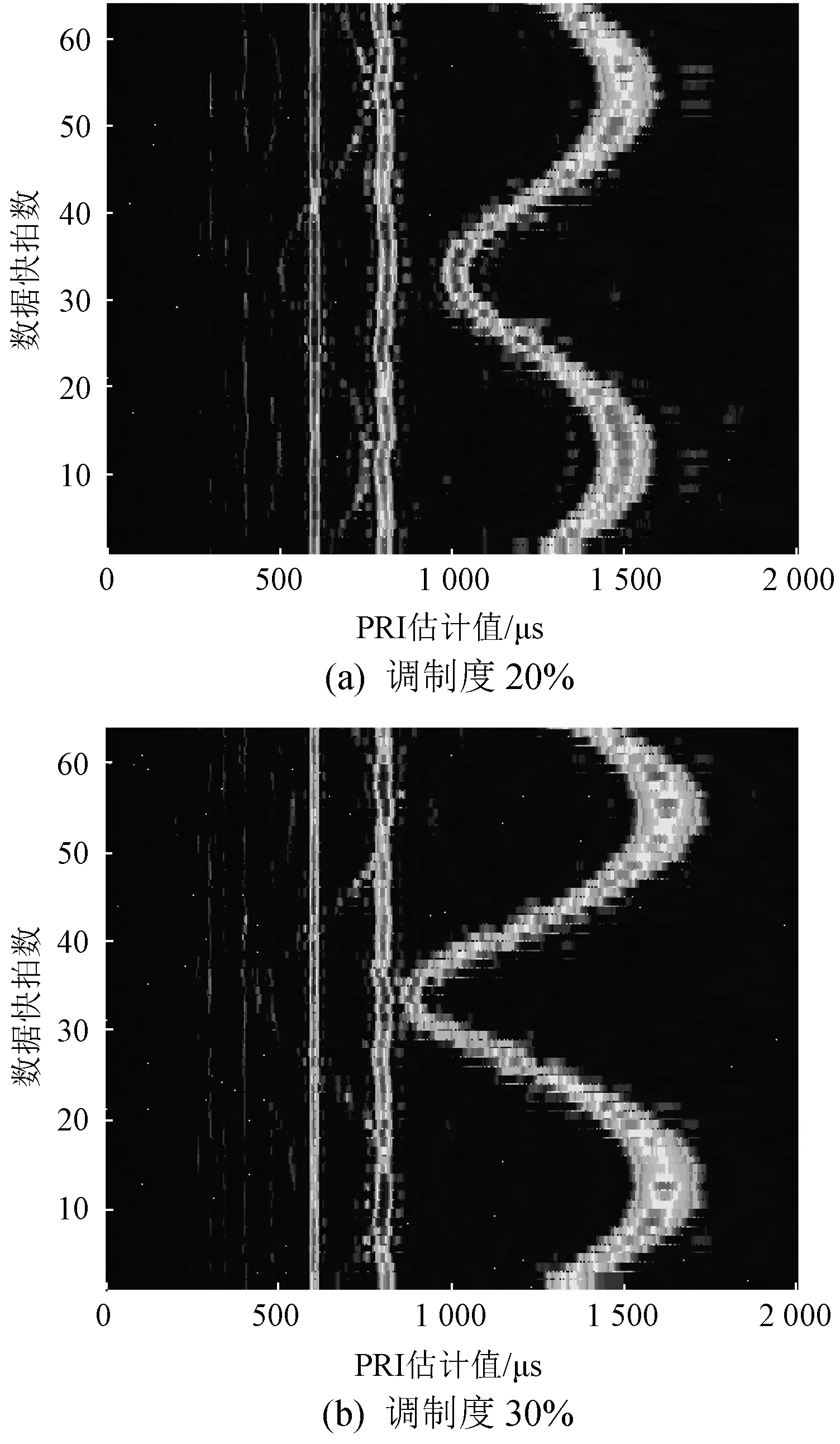
图7 增大重频调制度后的二维短时PRI变换谱图
由图7可知,混合了3种调制类型的目标脉冲信号被清晰准确地分选出来,不同PRI调制类型的信号分选及PRI参数估计结果如表2所示。

表2 脉冲分选及PRI参数估计结果
结果表明,本文提出的短时PRI变换算法对固定重频信号、重频抖动信号及重频正弦调制调制度30%以内的信号有良好的分选效果,能够准确估计出目标中心PRI值,估计误差可以控制在很小的范围内。由于采用了短时分析的方法,算法能够获取目标PRI的短时变化规律,通过对变换谱进行二维重排,能够实现多目标的PRI平面显示和实时更新,以便对目标的最新PRI动态进行观察和跟踪。
短时PRI变换算法能够获取更丰富的目标二维PRI成像信息,有利于抗同重频信号的干扰。相对于传统的一维信息,更加适合各类智能化目标,曲线提取算法的应用。
4 结论
针对传统PRI变换法和修正PRI变换法无法描述和显示复杂调制PRI信号的变化规律,以及平面变换法无法实现完全自动分选识别的问题,提出了一种短时加窗的PRI变换算法。仿真结果表明,短时PRI变换算法能够在快速分选识别目标的同时,获取目标PRI的短时调制信息,对固定重频、重频抖动和重频正弦调制调制度30%以内的目标信号具有优良的分选识别和跟踪显示性能,为多目标平面显示技术提供了新的思路。

