颜色读数和物质浓度的辨识问题探究

刘世奇 刘赵涵

华北水利水电大学水利学院（450007）

0 前言

根据实测数据建立数学模型，并对模型进行评价。我们以物质浓度为因变量，以B，G，R，H，S为自变量，运用多元回归的思想建立函数表达式，运用MATLAB软件进行求解，并求出各个系数，进而得到函数关系式，即只要输入颜色读数，就能得到对应的二氧化硫的浓度值。虽然求出了颜色读数与浓度的表达式，但该式并不能表示实际所对应的函数值（二氧化硫浓度）存在一定的误差。如当我们将二氧化硫浓度为20 ppm时的颜色读数带入函数表达式时所求出来的浓度值并不等于20 ppm。这里我们不妨将实际浓度与所得浓度作差比较得到偏差加以平方得到残差值和进而得出该模型的优劣。

1 模型的建立与求解

1.1 模型建立

设随机变量y与普通自变量B，G，R，H，S满足线性关系：

y=b0+b1B+b2G+b3R+b4H+b5S+ε

其中 b0，b1，b2，b3，b4，b5， 是待定系数，ε是随机误差。

yt=b0+b1Bt+b2Gt+b3Rt+b4Ht+b5St+ε，（t=1,2，L，n）

其中，ε1，ε2，L，εn……相互独立且服从同一正态分布。

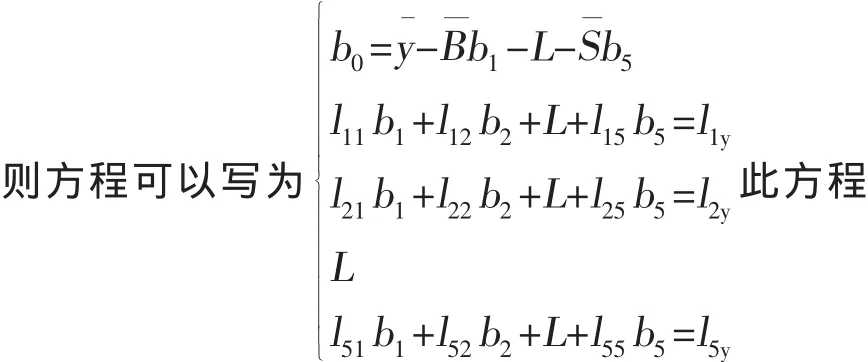
组的解b^0，b^1，b^2，b^3，b^4，b^5就是待定系数 b0，b1，b2，b3，b4，b5的最小二乘估计值，即y^t=b^0+b^1B+b^2G+b^3Rt+b^4Ht+b^5S

1.2 模型求解

我们运用MATLAB进行辅助运算，运算过程及运算结果，得出b^0，b^1，b^2，b^3，b^4，b^5。 于是y^=5 028.8+0.4R-7.2B-14.5S-14.6H，但这个模型与原数据真实模型还有一定的误差，从表1中我们可以看出相关系数r2=0.891，查阅资料发现r2越接近于1，函数模型对于原数据的拟合程度越好。可以认为，该模型对原数据的符合程度为89.1%。

利用模型原理，建立两个新的模型。这两个新模型对于原模型来说，一个是在数据量上进行减少，一个在颜色维度上进行减少。

表1 数据对模型的影响

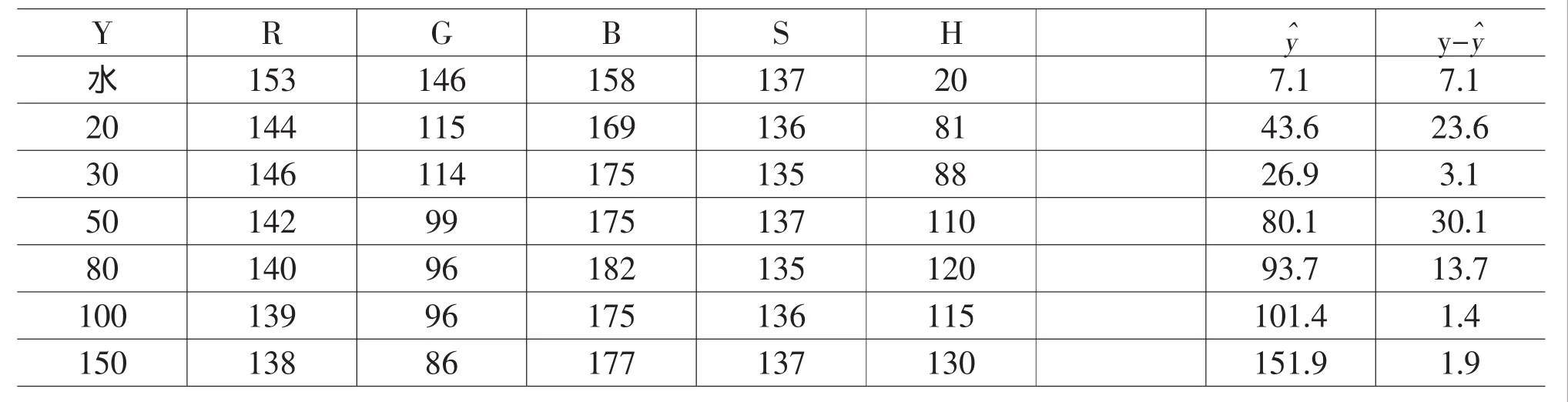
表2 二氧化硫浓度

1）数据量对模型的影响：利用建立的函数模型，在数据的选择上我们设置一个限制，就是减少每组二氧化碳浓度所对应的颜色读数，利用公式：y^=L^0+L^1B+L^2G+L^3R+L^4H+L^5S建立数据量减少时物质浓度与颜色读数的多元回归模型。

2）颜色维度对于函数模型的的影响：在数据选择上决定删去色调H，建立一个与之前相比少一维的函数回归模型即：y^=K^0+K^1B+K^2G+K^3R+K^4S，运用MATLAB进行运算，来讨论数据量对模型的影响。从表1中我们发现：

r2的值与之前相比更接近于1，而F检验、残差均方RMSE也都比原模型数据要好。所以当减少数据量的时候，并不会对原模型造成影响。当对颜色维度进行减少时，r2的值与之前模型相比更接近于1，残差均方RMSE也比颜色维度减少前要小。所以我们得出结论：当颜色维度减少时，并不会影响原模型。

2 模型的检验

我们将二氧化硫浓度与颜色读数模型进行检验，检验其是否符合实际情况；随机挑选几组数据带入到我们求解出来的函数模型，运用Excel，计算实际二氧化硫浓度Y与计算出来的二氧化硫浓度Y（见表 2）。

3 模型评价与推广

3.1 模型评价

颜色读数与物质浓度模型的建立，是为了减少观测者由于色差和对颜色敏感程度的影响，从而达到科学、精准、方便地获取待测物质浓度的一种方法。我们运用了统计回归、模糊数学的方法和思想，使得该模型更具有科学性和可靠性

3.2 模型优点

本模型中我们使用线性回归的方法，很好地反映了要素之间的数量关系。本模型更具有普遍性，在相同类型的情况下，依然能对问题很好地建模。

3.3 模型缺点

我们在进行模型假设的时候，假设了所有颜色读数与物质浓度都是线性关系，忽略了数据的非线性关系，从而造成了一定的误差。在数据选择上我们是将数据平均后再带入模型的，并不能代表数据的整体趋势。

3.4 模型推广

本模型具有很好的应用前景，如我们可以将本模型进行改进应用到汽车受损部位的修补，可以运用此模型进行化学物质的检验，或者对食品进行营养物质的检测。