充分挖掘教材 探求分数本质——以《分数的认识》教学为例

陈 飞

一、厚积薄发，探求分数本质

1.何谓分数。

分数概念起源于“分”，在表达平均分结果的时候，遇到了分的结果比1 还要小的情况，这只用自然数显然是不够的，于是引进了分数。这时候认识的分数，都是把一个物体平均分成若干份，表示这样的一份或几份，这就是分数的初步认识。后来扩展到不但可以把一个物体平均分，如果把一些物体、一个计量单位等看成一个整体，平均分后，其中的一份或者几份，可以理解为是这个整体的几分之一或几分之几。

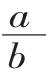
（1）平均分：把单位“1”平均分成b 份再取出a 份。

（2）部分与全体的比较：全体为b 时，a 是b 的部分。

（3）小数的另一种记法。

（4）除法运算的结果：表示a除以b 的商。

（6）测量：用来测量一个不满一个单位量的量的数值问题。

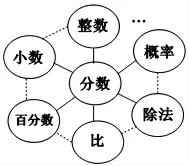
2.“分数的认识”教学分为几个阶段。

为使学生更好地理解分数的含义，教材采用螺旋上升的安排，分两个阶段学习：

第一学段，结合具体情境初步理解分数的意义，能认、读、写简单的分数。

第二学段，进一步认识小数和分数；探索小数、分数和百分数之间的关系，并会进行转化（不包括将循环小数化为分数）。

教材中的教学内容与编排顺序是：认识几分之一，认识几分之几（三年级上）；分数的意义，分数与除法的关系，真分数、假分数和带分数，分数与小数的互化（五年级下）。

3.教材编排的依据。

教材这样编排是基于学生的思维发展顺序，学生认识分数的过程，通过思维发展方式依序分为四个阶段：

（1）用面积的“部分—整体”表示分数，认识分数的面积模型。

（2）用集合的“子集—全集”表示分数，理解分数的集合模型。这也是“部分—整体”的另一种形式，与分数的面积模型密切相关。但学生在理解上难度更大，关键是单位“1”不再是一个物体了，而是把几个物体看作单位“1”，所取的“一份”也可能是“几个”。集合的“子集—全集”表示的就是分数的“集合模型”，这需要学生有更高的抽象思维能力。

（3）用数线上的点表示分数，感受分数的数线模型。

用数线上的点表示分数就是分数的“数线模型”。它把分数化归为抽象的数，需要学生具有更高的抽象思维水平。

（4）用除法和比表示分数。

二、巧妙约取，另辟教学蹊径

1.联系自然数来初步认识分数。

《分数的初步认识》是学生第一次建立分数的概念。教材编排有以下特点：

（1） 由一个物体组成单位“1”。如一个月饼、一张纸片等。

（2）只出现常见的分母比较小的分数（分母一般不超过10）。

（3）只认识真分数和分子分母相等的假分数。

（4）不正式定义分数，只通过直观手段建立初步的分数概念。

课堂结构一般是：

（1）巧设生活情境，引出分数。

（2）借助整数经验，创造分数。

（3）在丰富的数学活动中深化认识，理解分数。

［案例1］情境与冲突。《分数的初步认识》教学片断。

出示主题情境图，并引导学生思考：

①把4 个苹果平均分给2人，每人分得几个？

②把2 瓶矿泉水平均分给2人，每人分得几瓶？

考虑到工程施工中预埋套筒与连接钢筋对位时可能出现偏位情况，因此针对该试验选取试件H400-16、H400-16-2和H400-16-4，研究其在偏移距离0 mm、2 mm、4 mm条件下的试件承载力。结果如图13所示。

结合学生的交流，教师揭示：每份分得同样多，数学上叫做“平均分”。

③把1 个蛋糕平均分给2人，每人分得多少？

结合学生的交流，自然引出“一半”。

④每人分得的苹果、矿泉水可以用以前学过的数来表示，那“一半”该用怎样的数来表示呢？

学生交流各自的想法，教师结合学生的交流，揭示课题：认识分数。

“平均分”是初步认识分数的基础，在分配苹果、矿泉水和蛋糕的过程中，教师巧妙引导，唤醒学生“平均分”的经验，为初步认识分数做好铺垫，使学生实现由自然数到分数的和谐过渡。

［案例2］探索与建构。《分数的初步认识》教学片断。

①直观感知，初步认识。

引导：我们把蛋糕平均分成了几份？“一半”是其中的几份？

②动手操作，深化认识。

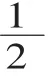
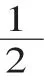
③观察判断，拓展认识。

学生交流，并说明判断理由。

2.分数的意义教学要从单位“1”的意义建构着手。

《分数的意义》是学生对分数学习的不断深入与推进，真正揭示分数的意义。其特点是：单位“1”变成了一些物体，正式定义分数，用规范化的数学语言建构分数的意义。

教学时，重点突出单位“1”的抽象，通过建构分数的“面积模型”、“集合模型”和“数线模型”，使学生理解单位“1”作为标准量和单位量的内涵。不仅要学生用形式化、规范化的数学语言表达对分数意义的认识，更应引导学生深入建构每一个具体分数的意义。课堂结构一般是：

（1）回顾面积模型（一个物体）。

（2）建立集合模型（一些物体）。

（3）感受数线模型（分数的本质）。

（4）深化对分数意义的理解。

［案例3］分数的“面积模型”→“集合模型”。《分数的意义》教学片断。

师：（往学生面前一站）认识吗？张老师能用自然数来表示吗？

生：用“1”表示。

师：除了人以外，还有什么也可以用“1”来表示呢？

生：1 块黑板……

师：还能说吗？

生：我们的一个班级也能用“1”来表示。

师：3 个苹果能用“1”表示吗？

生：能。

师：怎么看起来3 个苹果就是“1”？

生：放在一个盘里。

生：看成1 行。

师：把3 个苹果看作一个整体，就能看成“1”。

（把3 个苹果框起来）

师：那6 个、9 个、18 个苹果……也能看成“1”吗？

生：能。

师：如果把3 个苹果看作“1”，那6 个苹果应该看作几？

生：2。

师：为什么？

生：3 个苹果是“1”，6 是2 个“1”，就是“2”。

师：（出示12 个苹果）有4 个这样的“1”，就是几？

生：4。

师：有5 个这样的“1”，一共是几个苹果？

生：15 个。

师：3 个苹果看成的“1”就成了一个计量单位。在数学上，可以称作单位“1”。

单位“1”的含义应建立在对“1”（面积模型）的理解上，因此教师由表示一个物体的自然数1 引入，然后过渡到可以表示一些物体（集合模型）组成的整体的自然数“1”，“1”的内涵获得了一次重要的拓展和提升。那么如何帮助学生实现由“1”向单位“1”的实质性跨越？教师将学生置身于实际计量的数学活动中，让学生通过观察、比较认识到无论把什么看作“1”，只要包括几个这样的“1”，就可以用“几”来表示，从而在计量的背景下帮助学生丰富对单位“1”内涵的把握。

［案例4］建构分数的数线模型。《分数的意义》教学片断。

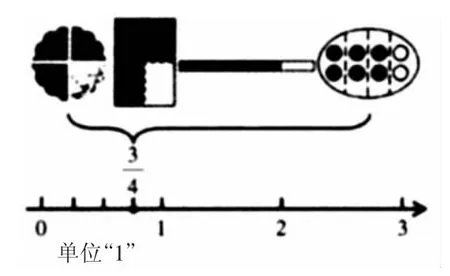
生：把数轴延长，在2 个“1”这么长，就是2。

师：如果不满单位“1”就用分数来表示，如果满了单位“1”，有几个单位“1”就是几。

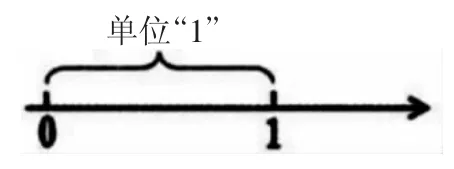
生：很简单!只要把它平均分成3 份，再表示出这样的1 份就行了。

（学生上讲台来指）

三年级学习分数，建立在面积模型（部分—整体）维度上，但随着分数学习的不断深入，在五年级的学习中，应该让学生体会到分数的集合模型和数线模型，让学生认识分数的本质，在抽象层面上建构起一般分数的意义。

三、仔细回味，教材研读味无穷

1.博观而约取，领会知识内涵。

教材研读要着眼于对文本内涵的挖掘，抓住知识的本质，开发出能达到更广泛、更深刻的教育目的的知识内涵。比如在确定《分数的意义》的教学方法前，得先问问自己，分数的本质何在？分数的意义到底是什么？你是否已经准确把握了教学内容？其实，我们应该在“怎么教”前先思索“教什么”，了解教学的内容，挖掘内容的本质，争取做到教得清楚，让学生学得到位。

2.厚积而薄发，发展深度课堂。

教师在领会知识内涵后，才能更好地梳理教学体系，把教材中零碎的数学知识进行归类，明确知识在体系中的地位，分析不同层次的教学要求，确定每节课的具体目标，并且落实到位。