基于GIS 和地理加权回归的砂田土壤阳离子交换量空间预测①
王幼奇,张 兴,赵云鹏,包维斌,白一茹*
(1 宁夏大学资源环境学院,银川 750021;2 旱区特色资源与环境治理教育部国际合作联合实验室,银川 750021)
土壤阳离子交换量 (CEC) 直接反映土壤保蓄、供应和缓冲阳离子养分的能力,同时也影响着土壤有机质、酸碱度和土壤结构等性质[1-2]。因此CEC 通常被作为土壤质量评价指标之一,同时也是土壤施肥和改良等的重要依据。砂田是干旱半干旱区农民在长期生产实践中探索形成的一种独有的保护性耕作方式,具有保温增渗、抑制土壤蒸发和防止侵蚀等作用[3]。近年来随着宁夏硒砂瓜产业的快速发展,砂田在发挥其巨大经济和生态效益的同时,也面临着由于长期耕作导致土壤肥力下降、质量退化等一系列严重问题[4]。因此精准预测砂田土壤CEC 空间分布规律对于防止砂田退化和提高土地生产力具有积极作用。
目前,基于地统计学的克里格插值方法在土壤要素空间预测中最常用[5]。普通克里格插值法(OK)对于样点数量和样点本身的数据质量具有一定的依赖性,土壤自身具有的强变异性使得在复杂环境下使用OK法对土壤属性进行空间插值已不能满足当前要素空间预测对于精度的要求[6]。因此利用辅助信息协助变量进行空间插值的方法如回归克里格(RK)等得到了极大的应用。RK 可以综合多个变量对土壤属性进行空间插值,有效提高了预测精度,但土壤属性的强空间变异性使得最小二乘法(OLS)这一全局模型无法很好地体现土壤属性的局部特征[7]。地理加权回归模型(GWR)作为一种有效处理回归分析中空间非平稳性和空间依赖性的局部模型,近年来被广泛应用到科学研究中[8-9]。如江振蓝等[10]探讨了GWR 模型在土壤重金属高光谱预测中的适用性及局限性;王合玲等[11]应用GWR模型对艾比湖土壤有机质和土壤因子响应关系的空间非平稳性进行了研究;袁玉芸等[12]利用传统回归和GWR模型分析于田绿洲表层土壤盐分及其影响因素的空间非平稳性。以上研究均表明GWR模型对存在空间非平稳性的数据具有更强的解释能力和估计精度。地理加权回归克里格法(GWRK)是将GWR 模型与RK 法相结合,综合多个变量对土壤属性进行局部空间插值,提高了插值精度,能更好地反映出土壤属性的局部变异情况[13]。目前,关于宁夏砂田土壤属性空间插值的研究多使用普通克里格插值法[14-15],对于将GWR 模型应用在土壤要素空间插值上的研究较少。本文以砂田土壤为研究对象,通过分析土壤CEC 及其影响因素之间的相关性,验证和比较OK、RK 和GWRK 的空间制图效果和插值精度,以期为土壤CEC 空间变异研究和土壤肥力管理提供科学依据。
1 材料与方法
1.1 研究区概况
研究区位于宁夏中卫市香山乡(图1),属于宁夏中部干旱带,地处 36°57′ ~ 37°07′N,104°56′ ~105°15′E,区内气候为温带大陆性气候,多年平均气温6.8 ℃,年均降水量247.4 mm,降雨多集中于7—9月。全区地势南北高中间低,平均海拔约1 740 m,土壤类型主要为淡灰钙土。天然植被主要以旱生灌木、半灌木、耐寒的蒿属和禾本科草类为主。土壤基本理化性质见表1。

图1 研究区样点分布Fig. 1 Distribution of soil sampling sites in study area

表1 研究区土壤基本理化性质Table 1 Soil physicochemical properties in study area
1.2 样点布设与数据采集
以香山地区行政区划图为底图,在研究区域采用1.5 km × 1.5 km 网格布点方式进行采样。实际采样过程中有些样点落在村庄、道路等地,通常在附近200 m 内进行调整,并用GPS 记录调整后的坐标,共布设108 个样点。使用土钻采集根层土壤样品(0 ~20 cm)。样品带回实验室后经自然风干,剔除植物残根及石砾等,碾磨分别过10 目和60 目筛待测。CEC的测定采用乙酸钠-火焰光度法[1]。土壤有机质采用重铬酸钾氧化-外加热法测定[2]。土壤机械组成采用激光粒度仪(MS3000,Malvern instruments)测定,粒径分级标准采用美国制[16]。
1.3 研究方法
1.3.1 回归克里格法 回归克里格法(RK)考虑到土壤属性空间变异驱动因子的复杂性,将线性回归与克里格插值相结合。当目标变量与辅助变量存在相关关系时,先通过对目标变量和辅助变量的相关性分析和线性逐步回归拟合,建立目标变量与辅助变量的多元(或一元)回归关系,得到趋势项。然后对所得残差项进行半方差分析,并使用普通克里格法对残差项进行空间插值,最后使用栅格计算器将趋势项与残差项两项相加,即为回归克里格的插值结果。公式表达为:

式中: z(s) 为目标变量在s处的预测值,m(s)为使用线性逐步回归得到的趋势项, ε(s)为使用普通克里格插值得到的残差项。
1.3.2 地理加权回归克里格法 地理加权回归克里格法(GWRK)是通过对目标变量和辅助变量进行地理加权回归拟合,得到局部回归的残差项,然后使用普通克里格插值法(OK)对所得残差项进行插值。GWRK 将RK 中的全局回归(式2)转换成地理加权回归模型(GWR)的局部回归(式3),能更好地体现土壤属性空间变异的局部变化。
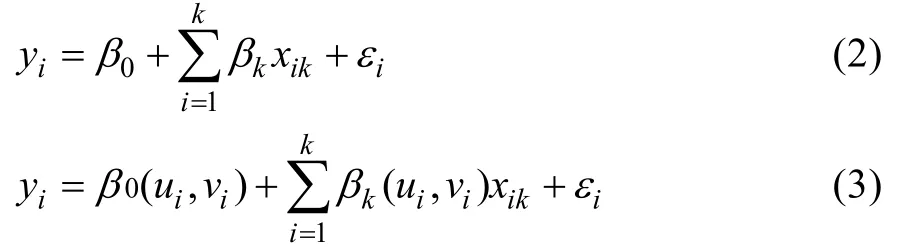
式中:yi为样点i的因变量;xik为第i个样点上第k个变量的观测值;(ui,vi)为样点i的地理空间坐标;β0为回归的常数项;βk(ui,vi) 为第i个采样点上的第k个回归参数;εi为残差项。如果βk(u,v)在空间保持不变,则模型(式3)就变为全局模型(式2)。
1.3.3 模型精度检验指标 为了评价模型的预测精度,选取以下3 个指标对模型进行精度评价。平均误差表示预测值与实测值偏差的算术平均值;均方根误差表示预测值与实测值偏差的平方和观测次数比值的平方根。均方根误差对预测中特大或特小误差反应比较敏感;相对精度改进值(RI)是表示衡量模型模拟效果是否优于仅对实测值取平均值的指标。

式中:ROK、RRK和RGWRK分别代表OK、RK 和GWRK拟合值与实测值的相关系数,RI 值为正值即表示RK、GWRK 较OK 的预测精度高,值越大说明预测精度提高地越多;RI 值为负值则表示RK、GWRK预测精度低于OK。
1.4 数据处理与分析 采用SPSS 18.0 和Excel 对数据进行描述统计分析、相关性分析和逐步回归分析,使用GS+9.0 和ArcGIS 10.2 软件对数据进行地统计分析和空间插值。为排除异常值对半方差函数稳健性的影响,依据3σ 准则对原始取样数据进行了异常值识别,异常值用正常的最大或最小值代替,后续分析采用处理过的原始数据进行计算。为验证模型的预测精度,随机选择86 个样点作为建模样点进行空间插值,22 个样点作为验证样点用于分析插值精度。
2 结果与分析
2.1 土壤CEC 描述统计分析
描述统计表明(表2),建模点和验证点CEC 均值分别为9.82、10.47 cmol/kg,含量变化范围分别为5.75 ~ 14.87 cmol/kg 和6.15 ~ 15.83 cmol/kg。研究区土壤CEC 均值为10.145 cmol/kg。根据土壤保肥能力分级方法[17],供肥保肥能力弱的样本数占总样本数的60.19%,供肥保肥能力中等的占39.81%,说明研究区土壤供肥保肥能力多处于低水平。偏度和峰度数值均较小(<1)。从变异程度看,建模点和验证点CEC变异系数分别为17.57% 和21.02%,属中等变异。经K-S 非参数检验,建模点和验证点的P值均大于0.05,数据服从正态分布。
2.2 土壤CEC 与土壤理化性质的相关性分析
影响土壤CEC 含量的因素有很多,有机质及矿质胶体的数量与性质是决定土壤CEC 的重要因子[2]。相关学者亦研究发现CEC 与有机质、土壤质地存在显著相关性,明显影响CEC 在区域上的分布特征[18-19]。因此为提高CEC 预测精度、更好展现其空间分异特征,本文从CEC 与有机质、矿质胶体的耦合关系为出发点,选取了研究区土壤有机质、质地与CEC 进行相关性分析[20]。表3 可以看出,CEC 与有机质、砂粒、粉粒和黏粒呈显著相关关系。其中CEC 与有机质、黏粒和粉粒呈显著正相关,与砂粒呈显著负相关。

表2 土壤CEC 的描述统计特征Table 2 Descriptive statistics of soil CEC
2.3 土壤CEC 的回归模型与半方差模型
2.3.1 逐步回归分析 在相关分析基础上,选择有机质、黏粒、粉粒和砂粒作为辅助变量,采用逐步回归筛选出对各个回归模型具有显著贡献的回归参数。逐步回归结果表明(表4),有机质和砂粒是对CEC 插值的最佳自变量。方差膨胀因子(VIF)为1.12,小于7.5,说明自变量间不存在共线性。调整后的决定系数为0.567,说明OLS 模型对CEC 的方差解释度为56.7%。拟合模型如下:y= 7.478+0.964x1-0.052x2,式中,y为CEC;x1为有机质含量;x2为砂粒含量。为了便于对比,应用GWR 模型时,同样选用有机质和砂粒进行建模。

表3 土壤CEC 与土壤理化性质的相关性Table 3 Correlation between soil CEC and other soil physicochemical properties

表4 土壤CEC 与土壤理化性质的逐步回归过程Table 4 Stepwise linear regression process of soil CEC with other physicochemical properties
2.3.2 地统计分析 对CECOLS 残差和GWR 残差进行描述性统计分析。OLS 残差变化范围为 -1.49 ~4.02,均值为0.004 7;GWR 残差变化范围为 -1.57 ~4.44,均值为 -0.0345。经K-S 非参数检验,两种回归方法所得残差均服从正态分布。在GS+9.0 中对实测值、OLS 残差和GWR 残差进行半方差函数模型拟合(表5)。可以看出,三者均可用球状模型拟合。块金值(C0)代表随机因素带来的变异,通常由区域变量的变异性和测定误差所造成[21]。三者的块金值(C0)均小于0.3,表明CEC 由测定误差或土壤性质带来的随机变异较小,空间变异主要受结构性因子影响。块金系数(C0/(C0+C))表示由随机因素引起的空间变异占系统总变异的比例。一般来说,比值<25% 时空间变异性表现为强空间相关性,介于25% ~ 75% 时表现为中等强度空间相关性,比值>75% 时表现为弱空间相关性[17]。实测值、OLS 残差和GWR 残差块金系数分别为8.50%、6.36% 和7.02 %,比值均在25% 以下,说明CEC 及其残差具有强烈空间自相关。

表5 土壤CEC、OLS 残差和GWR 残差的半方差模型参数Table 5 Semivariance parameters of soil CEC and regression residuals of OLS and GWR
2.4 土壤CEC 的空间分布特征
利用OK、RK 和GWRK 3 种方法进行空间插值得到的CEC 空间分布图。根据图2 可以看出,3 种方法得到的结果中CEC 的分布格局大致相似,即研究区西部的CEC 要大于东部,高值区分布在西北、东北和南部,CEC 存在从这些地区向中东部逐渐减小的趋势。CEC 预测值范围分别为5.75 ~ 14.88、5.77 ~ 13.00、5.52 ~ 12.90 cmol/kg,各方法基本一致。从制图效果看,OK 法插值图较为粗略,RK 法的插值结果体现了CEC 随着有机质和砂粒的变化情况,但是斑块的边界较为零碎,这与现实中CEC 的空间渐变特征不相符。GWRK 法不仅保留了回归分析中CEC 随土壤理化性质变化的丰富细节,还反映出CEC 的空间渐变特征,斑块边界更为光滑,感官上更符合CEC 的实际分布状况。为了更好地反映3 种插值模型对区域土壤CEC 的预测精度,利用平均误差、均方根误差和RI 值对插值结果进行精度评价。
2.5 不同插值方法的空间预测精度评价
表6 对OK、RK 和GWRK 方法进行了精度评价。结果表明3 种方法的平均误差基本接近于0,表明了所构建模型的预测具有无偏性;均方根误差OK>RK>GWRK,范围为1.084 ~ 1.853,趋近于1,说明所构建模型的误差有效。从相对精度改进值来看,RK 和GWRK 法相较于OK 法拟合精度分别提高了40.49%和41.50%,表明3 种插值方法中GWRK法插值精度最高,为最优插值模型。

图2 三种插值方法下土壤CEC 的空间分布Fig. 2 Spatial distribution of soil CEC by OK, RK and GWRK interpolation

表6 OK、RK 和GWRK 方法的精度评价指标对比Table 6 Precision evaluation of three interpolation methods
3 讨论
研究区土壤CEC 均值为10.145 cmol/kg,供肥保肥弱的样本数占总样本数的60.19%,研究区土壤保肥供肥能力较弱。前人的相关研究也发现了类似情况[4,15]。其产生原因可能与当地土壤母质和耕作制度有关。研究区处于我国西北内陆腹地,土壤类型为低肥力的淡灰钙土,自然环境条件限制了当地土壤的肥力水平。再加上研究区有覆砂的传统耕作制度,农民施肥难度大,外源性的有机肥施入量不够,导致当地土壤肥力偏低。砂田土壤CEC 在空间上展现出高度变异性,在研究区地形、气候和母质相对均一的情况下,土壤理化性质可能是导致土壤CEC 在空间上呈现出较强变异性的重要原因。其中有机质中胶体成分在土壤固相中所占比例较大,土壤胶体是CEC 的载体,随有机质含量增加,CEC 也随之增加。同时在土壤颗粒组成中,黏粒胶体集中了80% 以上的负电荷,土壤黏粒含量愈高,CEC 就越高[18-20]。相关学者亦研究发现CEC 与有机质、土壤质地存在显著相关性,明显影响CEC 在区域上的分布特征。砂田CEC 与土壤有机质、黏粒和粉粒呈正相关,与砂粒呈负相关,即在有机质和黏粒含量高的地方,CEC相对充足。针对这一情况,建议在后续农业生产过程中增施有机肥,推广轮作制度以培肥土壤,从而提高作物产量。
空间插值技术是利用采样点数据对研究区内未知点进行预测的方法。常用的空间插值方法有普通克里格法、回归克里格法等[22-23]。张慧智等[24]对比了普通克里格、泛克里格和回归克里格在土壤温度空间预测中的效果,发现回归克里格法预测精度最高,能够更好地表达复杂地形地区的局部变异。Hengl 等[25]采用回归克里格对土壤有机质含量进行空间预测,发现其预测精度较普通克里格表现更好,均方根误差数值更低。但是,土壤理化性质与土壤CEC 之间的相关关系因地而异,局部区域的CEC 与土壤理化性质关系可能与做全局分析时得出的结论相反,这在回归克里格中没有考虑。GWR 模型能将数据的空间信息纳入分析过程,通过计算回归模型的局部参数来解决地理数据中存在的空间自相关性及空间非平稳性问题,从而提高模型的拟合优度及模拟效果[26]。本文对3 种插值模型的精度分析结果也证明了GWRK 法在空间制图方面表现出更丰富的局部细节和更光滑的空间渐变特征。因此,在后续土壤属性的空间制图研究中,应注重GWRK 法在土壤属性空间插值中的应用。
4 结论
1) 相关分析表明,土壤CEC 与有机质、黏粒和粉粒含量呈显著正相关,与砂粒含量呈显著负相关。
2) 地统计分析表明,土壤CEC 及其插值残差均可用球状模型拟合;实测值、OLS 残差和GWR 残差块金值均小于0.3,说明其空间变异主要受结构性因子影响;块金系数分别为8.50%、6.36% 和7.02%,表现出强烈空间自相关。
3)从插值效果和精度分析来看,GWRK 是3 种模型中插值效果最为理想的;RK 和GWRK 法相较于OK 法拟合精度分别提高了40.49% 和41.50%,3种插值方法中GWRK 法插值精度最高,为最优插值模型。

