基于博弈论的城市轨道交通与常规公交协同定价分析
姚 兰
(兰州交通大学 交通运输学院,甘肃 兰州 730070)
0 引言
轨道交通与常规公交作为城市公共交通的骨架与核心,在满足城市居民日常出行、解决城市交通拥堵方面起着重要的作用[1,2]。城市公共交通可持续发展的关键在于票价的制定,科学、合理的票制结构会均衡客流、减少交通拥堵,对于城市居民出行效率提高、整个城市经济的发展有着促进作用[3]。因此,为了提高城市公共交通的使用率,需制定合理、适宜的票价策略。政府作为城市公共交通的宏观调控者,在交通工具、交通设施、内部管理、成本控制等方面扶持与强化监管下,使得公共交通在很大程度上有了明显的改善与提升,政府补贴促进了公共交通行业的可持续发展[4-6]。城市轨道交通与常规公交共同服务于城市居民,两者之间必然存在着竞争关系,故用博弈论理论来分析城市公共交通的定价问题[7],并考虑相应的约束条件,会使城市公共交通系统中整个供应与需求的关系达到一种稳定的状态,促进城市公共交通的持续稳定发展。
1 博弈论在公共交通定价中的适用性分析
博弈论中有两个典型特征,即所有参与者都是理性人和所有参与者均希望实现自己的利益最大化,而从竞争问题的本质来看,都满足这两种特征。就城市公共交通定价问题来看,参与者主要包括乘客、政府和公交运营企业,乘客希望自己在出行过程中的花费最少,政府希望社会公益性最强,而公交运营企业希望收益最高。因此,博弈论能很好的解决城市公共交通定价问题[8]。
博弈论中经典例子之一的“公共地问题”,在分析城市公共交通定价中有着很大的相似性,参与者乘客、政府和公交运营企业三者之间相互约束,关系如图1所示。

图1 参与主体的博弈关系图
从图1可以看出,公交企业满足乘客的出行需求,政府在乘客的出行过程中提供公益性与福利性;公交企业通过为政府提供自身的收入与成本从而申请获得票价与补贴政策,而政府作为管理者理应对其进行管制;乘客作为消费者,有权对其票价政策监督和听证,三者之间相互约束。
2 博弈过程分析
2.1 票价与客运量之间的博弈分析
乘客在出行方式选择过程中,影响乘客广义出行费用的因素除了票价外,还有快速性、可靠性、舒适性、安全性等,但这些因素在短时间内一般不会变化,因此,公共交通客运量将受到票价变动的影响。客运量与票价之间的关系如图2所示。

图2 客运量与票价关系图
从图2可以看出,当票价上涨时,客运量逐渐减少,乘客的出行选择向另一种交通方式转移,相反,随着票价降低,客运量逐渐增加,乘客出行选择向该交通方式转移,即该交通方式吸引力增强。
2.2 票价与运营企业收益之间的博弈分析
运营企业的收益与票价、客运量、成本及政府补贴有关,当运营企业将其线路建成并投入运营后,运营成本基本可以看作已知量,政府补贴一般情况下变化不大,也可看作已知量,则运营企业的收益与票价和客运量有关。当轨道交通和常规公交在某OD区段内的总客流量保持不变时,票价在一定程度上又决定着客运量,因此,运营企业的收益很大程度上由票价决定。根据函数关系可得到两种公共交通的收益与票价关系如图3所示。

图3 收益与票价关系图
从图3可知,票价与收益的关系近似成抛物状,存在上升和下降两个阶段,当票价从0增长到P*时,收益也从0增加到了R*,此时收益最大,当票价超过P*时,收益呈下滑趋势。这是因为票价增长初期,票价处于乘客可接受范围,票价对客运量的影响不大,因此,运营企业收益随票价的增长而增长,当票价越过P*时,票价超出了乘客的预期范围,乘客可选择其他出行方式,此时的票价对客运量的影响较大,导致运营企业收益降低。从图中明显可以看出,运营企业如果想要获得最大收益,必须寻求该运输方式的最优票价P*。
2.3 轨道交通与常规公交之间的博弈分析
在城市公共交通系统中,轨道交通作为新加入者,会根据常规公交已有的票价策略制定出自己的最优票价,使自身收益最大化,当轨道交通制定出自己的票价策略后,常规公交会根据城市轨道交通所制定的票价从而调整自己的票价,当常规公交票价变化时,轨道交通又会调整自己的票价。这样经过n轮博弈后,双方都不能单方面通过改变自身票价来增加收益时,便达到了各自的最优票价,即博弈达到平衡。具体博弈过程如图4所示。
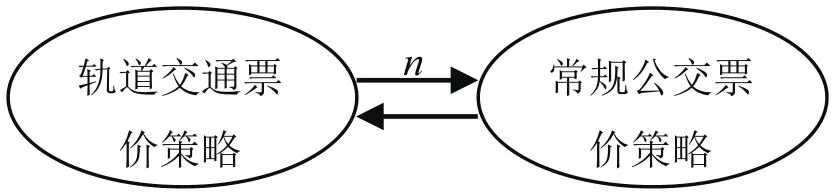
图4 轨道交通与常规公交博弈过程
2.4 运营企业与乘客之间的博弈分析
在城市公共交通市场中,运营企业与乘客之间也存在着博弈关系。乘客作为理性人,会尽可能的选择费用最小、效用最大的出行方式,而运营企业则通过票价调整使利益最大化,票价的变化影响了乘客对出行方式的选择,乘客对票价变化做出的反应又促使运营企业对票价的调整,从而吸引更多的客流量来增加自身的收益。这样经过n轮博弈后,双方都不能单方面通过改变自身的决策来增加收益时,两者博弈达到平衡。具体博弈过程如图5所示。
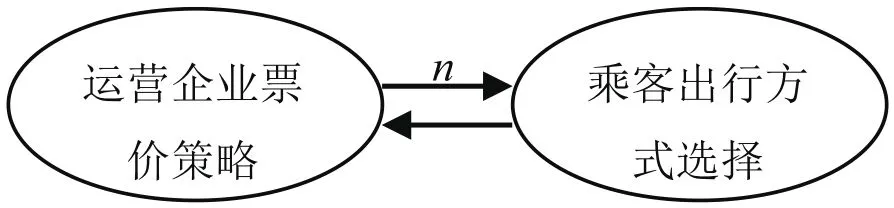
图5 运营企业与乘客博弈过程
3 模型建立与求解
3.1 双层规划模型建立
在城市轨道交通与常规公交博弈定价过程中,必须综合考虑到出行者的经济支付能力、政府相关政策、公交企业的运营成本等多种因素。所以,采用双层规划模型进行求解票价时,上层规划目标则可以设定为在政府限价政策约束下的公交运营企业收益最大化;而下层规划目标可以设定为乘客广义出行费用最小化。通过双层目标函数的动态求解,从而得到均衡解[9]。
上层规划模型可表示为:

下层规划模型中,假设乘客选择某种出行方式的客流量是一个连续变化的过程,则下层规划模型可表示为:

式中,Ri表示第i种交通方式的运营收入;Pi表示第i种交通方式的票价;qi表示第i种交通方式的客流量;Ci表示第i种交通方式的运营成本;Si表示第i种交通方式的政府补贴;Z表示乘客的广义出行费用;a,b表示待定系数;Vi表示出行效用;Q表示总客流量;1,2分别代表轨道交通与常规公交。
3.2 模型求解思路
城市轨道交通与常规公交票价定价过程,是一个完全信息条件下定价策略动态博弈的过程。双层规划模型的求解关键是在上层和下层规划模型中建立关系,即反应函数,通过反应函数可将双层规划模型转换成单层进行求解。本论述具体介绍采用灵敏度分析方法的求解思路。
首先,通过下层规划模型中客流对票价的导数来逼近反应函数,然后把反应函数代入到上层规划中,将问题转换为非线性问题,通过数学手段求解上层规划得到最优解,进而代入下层规划模型中得到新的反应函数,如此反复计算,最终求得双层规划模型的最优解[10]。
具体求解算法如下:
Step2:在初始条件即轨道交通与常规公交的价格策略集为{}下,求解下层规划模型中选择常规公交出行的乘客数量的问题,得到均衡解q2。
Step8:将得到的q1()带入上层规划中,即可求得轨道交通新制定的价格{}。
4 结束语
针对城市轨道交通与常规公交的定价问题,从博弈视角出发,分析了票价制定过程中各参与主体的博弈过程,建立了双层规划博弈模型,采用灵敏度分析法对该模型进行求解。
城市轨道交通与常规公交作为城市居民通勤的主要交通工具,对于提高居民的出行效率发挥着重要的作用。因此,政府作为公共交通的管理者,应该宏观调控两者的票价,提高公交运营企业的服务水平,同时,在票价制定过程中,采用博弈理论分析两者之间的定价过程,对公共交通合理分配客流、缓解城市交通拥堵发挥着重要的作用。

