基于时隙堆栈搜索的异构集群DAG调度策略

薛亚非，冯 钧

(1.南京师范大学 中北学院，江苏 南京 210046；2.河海大学 计算机与信息学院，江苏 南京 210098)

0 引 言

对于有向无环图应用，任务调度问题是并行计算和分布式计算的基本问题之一，该问题一般是NP难的，最优解仅限于该问题限制情形，该领域中启发式任务调度算法已得到广泛研究[1,2]。

组合优化问题有许多技术，已被应用到任务调度制导搜索算法中，可分为两类[3,4]：①随机制导搜索，其中使用随机过程，借助于候选解表示方法和随机候选解摄动过程。例如，文献[5]提出基于模拟退火算法的任务调度策略，通过涉及重复加热和冷却的退火过程使晶体结构处于更有序状态的概念。文献[6]提出基于禁忌搜索算法(Tabu)的任务调度策略，可避免在区域附近重复搜索。文献[7]提出基于模拟进化算法(simulated evolution，SE)的任务调度策略，通过使用选择和生成步骤从当前解决方案生成新的任务调度解决方案。②确定性制导搜索，使用确定性策略，对要解决问题的密切知识搜索候选解。例如，文献[8]提出基于TASK算法(TASK algorithm)的任务调度策略，算法缺点是重复执行步骤过多，计算复杂度过大。同时，当任务调度问题采用随机制导搜索策略时，存在问题[9,10]：①随机性可防止搜索在适当的搜索方向上快速进行。根据沿途发现的随机解，对于中型或大型网络搜索时间变化很长。②通常需要大量控制参数，这些参数通常由实验确定。这是严重的限制，因为反映实际执行环境的良好实验对于获得良好解决方案至关重要。

本文提出了基于时隙堆栈策略的确定性引导搜索算法，该算法对于异构集群系统的DAG调度特别有效，通过使用消除由慢速网络链路互连的节点之间的通信需求的“填充”操作来解决上述问题，实现算法性能提升。

1 问题模型

1.1 模型定义

应用程序可利用DAG模型G=T,E表示[11]，其中T是一组NT任务集合，E是一组NE边集。每个边eij=ti,tj∈E表示优先约束关系，指示任务ti应该在任务tj开始之前完成执行。任务ti具有与基线处理器平台上任务ti的执行时间相对应的权重τi1≤i≤NT，边缘eij1≤i,j≤NT具有与从pi到pj要传输的数据量对应的权重εij。

目标异构集群系统可以由无向图HC=C,LW分层表示，其中C=Ck1≤k≤NC对应于一组NC集群，而LW=lCiCjCi,Cj∈C对应于一组集群之间的WAN链路。每个集群Ck=P(k),L(k)包含一组处理器P(k)和用于在P(k)中的处理器之间进行通信的一组局域网(LAN)链路L(k)。

为了进行任务调度，异构集群系统可由非层次图模型NHC=P,L表示，其中[12,13]

(1)

在这一特定链接表示，给定链接lpipj，如果pi,pj都属于第k个簇C(k)，则该链接对应于L(k)中的LAN链接。否则，该链接对应于LW中的WAN链接。每个处理器pq都有一个(相对)计算功率因数wq；在处理器pq上执行任务ti需要τi·wq时间单位。同样地，令λpq,pr表示pq和pr之间链路的带宽的倒数，以便在εij·λpq,pr时间单元将εij从pq发送到pr。给定一个DAG模型G和一个异构集群模型NHC，本文解决的问题是找到一个高质量的调度，定义为从G到NHC的映射。解决方案的质量由最大完工时间、所产生的计划的总长度决定。

1.2 调度方案求解

可使用诸如图1所示的图形结构来表示调度表。在这个图中，虚线箭头表示存在分配给同一处理器的两个任务之间的执行顺序。

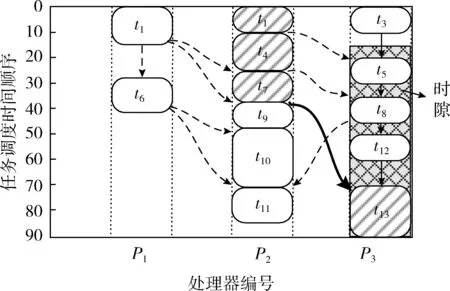
图1 关键路径(厚实线)和时隙模型

定义1[14]给定分配在同一处理器上的两个任务，tjl和tjm，对于tjl优先于tjm，表示为tjltjm，当且仅当l小于m时。符号“”用于表示执行顺序。当秩不同时，可用代替“”。

定义2[15]在同一处理器上连续分配的一组任务由tjl::tjm表示，其中tjl和tjm是分别具有最小和最大秩的两个任务。这个集合可被认为是一个时隙堆栈。时隙堆栈的顶部和底部元素分别是tjl和tjm。

1.3 调度计划评估

调度质量可用列表启发式方法评估。令AST(ti)和AFT(ti)表示任务ti的指定开始时间和分配完成时间。Tdata(ti)是从处理器φ(ti)执行任务ti的接收所有数据所需时间，Tavailφ(ti)是处理器φ(ti)可用时间。则可得

(2)

式中：compti,φ(ti)任务ti在处理器φ(ti)上的计算时间。下面列出其它有关定义。

定义4 计划调度的关键路径CP是任务和边缘的路径，从而导致该调度具有最小完成时间。CP中任务被称为关键任务。CP长度是进度的最大化。

定义5 给定任务ti，ti的关键前置任务(cpt(ti))是ti的前置任务，它最迟在ti的所有前置任务中完成数据传输。Tdata(ti)由ti的关键前置任务决定。

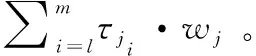
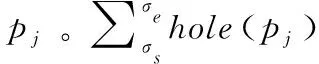
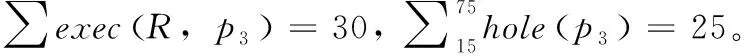
1.4 调度过程改进

在基于搜索的调度算法中，常用技术包括试图通过修改当前最佳任务调度来找到改进的任务调度，然后测试新调度是否优于当前最佳调度。如果新的调度计划更好(或者至少不是更坏)，那么在下一次迭代中，它被认为是当前最佳计划。新的调度表被认为是可接受的。如果新的调度表是可接受的，它将在下一次搜索迭代期间替换当前最佳调度。

该“修改和测试”方案导致在每次迭代中找到连续更好的任务调度的可能性。但是必须有一种方法生成新的调度计划，以有效方式搜索可能的解决方案空间。此外，生成的新调度必须具有有效的表示形式。下面给出如下两个表示函数：

函数1：ψ′1=ReassignR→pjψ。此函数通过使用以下步骤将集合R中的所有任务重新分配给处理器pj来更改调度方案ψ。

步骤1 每当调度ψ下任务tjk,tjk+1不是E∈G的元素时，将该对作为零加权伪边添加到DAG模型G中。

步骤2 按照拓扑顺序对得到的DAG模型进行排序，并构造包含一系列匹配对ti,pj的字符串。该匹配意味着任务ti被映射到处理器pj。

步骤3 替换pj匹配的处理器部分；亦即，对于tk∈N利用tk,φtk替换tk,pj。

步骤4 基于拓扑排序和在修改后的字符串中使用的匹配来构造新的调度。

这4个步骤通过在DAG中维护任务之间的优先约束来保证生成有效的调度。该函数的时间复杂度为O(TlogT)，其中T是任务的总数。这源于在步骤2中在DAG拓扑模型中对所有T任务排序所需的时间。

2 基于时隙堆栈的任务调度算法

2.1 算法描述

在所提基于时隙堆栈的任务调度算法中，可利用两个步骤获得高质量的解决方案：①使用基线算法生成基线调度。最近开发的算法，例如HEFT或HCPT算法[13,14]，可以快速地为大多数类型的目标计算环境生成良好的任务调度，可以用作基线算法。②使用确定性搜索过程改进基线调度。其实质为协调搜索过程，试图通过利用任务调度问题和目标计算环境先验知识来迭代地改进当前最佳解决方案。

所提算法采用两种技术以提高基线调度：①涉及找到当前调度的关键路径，并试图通过将任务移动到其它处理器来缩短完工时间，从而减少关键任务分配开始时间。②包括找到给定时间表中的所有可行时隙(在两个指定任务之间的处理器时间中的空闲间隙)，并检查是否有可能将一组任务插入到这些时隙中。如果成功地将任务插入时隙可显著缩短完成时间(执行DAG应用程序中的所有任务所需的时间)。这两种技术，分别称为推送和填充过程，以迭代方式执行，直到在搜索解决方案中没有进一步改进为止。算法1给出了任务调度的时隙堆栈过程形式化描述。

算法1：时隙堆栈过程形式化描述

(1) 利用现有算法(基于列表的启发式算法)生成调度计划ψ。

(2) Repeat

(3)利用推送过程获得新调度方案ψ′；

(4)利用填充过程获得新调度方案ψ″；

(5)在ψ,ψ′,ψ″中选取最佳调度→ψ；

(6) UntilK步迭代后→ψ不发生变化；

(7) Returnψ(当前最佳调度方案)

最初，该算法使用基线算法(例如，基于列表的启发式算法)获得基线调度。接下来，它重复时隙堆栈过程，直到K步迭代过程中解的质量没有改善为止。K是该算法中唯一的控制参数(通常设置为一个小值，如K=4或5)。当算法终止时，它返回迄今为止找到的最佳调度。算法中ψ′即为函数1～函数2中所定义的ψ′1和ψ′2。

触发任务与目标任务集定义方面，时隙堆栈操作试图通过重新分配任务来减少调度长度。在这些操作中，激励这种重新分配任务ti被称为触发任务，且由触发任务重新分配的相同处理器上连续分配一组任务，例如R=[tjl::tjm]，被称为目标任务集。对于所有推拉操作，都需触发任务ti和目标任务集R。

2.2 推送操作

给定触发任务ti和R中的目标任务，涉及触发任务ti目标任务到另一处理器上的操作称为推送操作。因此，推送操作可表述如下

(3)

图2 推送操作

示例中，假设触发任务是t5，目标任务集R具有t3和t4。由于t5推送t3和t4，两个目标任务被重新分配到产生最佳结果调度的任何处理器(在p1、p2和p3之间)。图2给出推送结果。任务t3和t4分别被移动到p1和p3，这导致了最大完工时间减少。

为执行推送操作，需一个目标任务集，可通过触发任务ti和目标任务tk之间的下列先决条件完成的，须满足：①tk和ti彼此独立；②φtk=φ(ti)；③tkti。推送操作目的是通过将目标任务推离当前处理器来更早地执行触发任务ti。为此，增加第3个条件。上述3个条件均满足ti和Bitsk(ti)位之间的任务tk。因此，Bitsk(ti)用作推送操作中给定任务ti的匹配目标集R。该算法过程见算法2所示。

算法2：推送操作

ProcedurePush_optc,Bitsktc→P

(1)R←Bitsktc；

(2) whileR≠∅ do

(3)在R中选取任务tr；

(4)P′←P中候选处理器；

(5)repeat do

(6) 在P′中选取处理器pj；

(7)ψ′←Reassigntr→pjψ；

(8) ifψ′可接受 then

(9)ψ←ψ′；

(10)P′←P′-pj；

(11)untilψ′可接受；

(12)R←R-tr；

(13) endwhile

在最坏的情况下，所有新生成调度都是不可接受的，该算法的时间复杂度是ORPTlogT。然而，由于新生成的调度可以在内环内被接受，所以平均时间复杂度会更小。

必须将Bitsktc的所有任务重新分配到P中处理器中。由于在典型的异构集群环境中存在大量的处理器，因此希望限制要考虑的处理器集。因此，对于给定目标任务，只有以下处理器被视为候选处理器，表示为P′：①分配至少一个任务的处理器；②在每个集群中没有任务分配的处理器中最快的处理器(具有最低的wq)。

以这种方式选择候选处理器原因如下：①如果在给定处理器上分配任务，则在该处理器上执行其它任务可以消除通信延迟。②可能还有其它有用的处理器，在这些处理器上还没有分配任务。当计算和通信成本都被考虑时，在可用处理器集合中每个集群中最快处理器也可能对某些任务有益。利用该操作，推送操作时间复杂度变为ORP′TlogT。

2.3 填充操作

给定分配给处理器pi的触发任务ti和分配给处理器pk≠pi的目标任务集R=tjl::tjm，涉及触发任务填充设置到处理器pi的目标任务的动作被称为填充操作。因此，该操作可以表述如下

Pull_opti,R≡ReassignR→φ(ti)

(4)

当填充目标任务时，将被重新分配给触发器任务处理器。这使得触发器任务和目标任务在同一处理器上执行，从而消除了它们之间的通信成本。填充运算的时间复杂度为OTlogT。

图3给出了填充操作的一个例子。在这个例子中，假设触发任务是t7，目标任务集R包括t3、t4和t5。因为t7填充R=t3,t4,t5，将3个目标任务重新分配给p7，从而减少最大完工时间。

图3 填充操作

要执行填充操作，填充操作需要一个目标任务集。这是通过在R=tjl::tjm中的触发任务ti和目标任务tk之间满足以下前提条件来实现的，必须满足以下条件：①必须存在一个边缘ejmi；②φ(ti)≠φtk。这两个条件称为填充条件。

给定目标任务ti，使用以下方法来确定目标任务集。首先，选择一个具有φ(ti)≠φcpt(ti)的任务cpt(ti)作为第一目标任务，这对应于R中的tjm。这种选择的原因是ti的指定起始时间严重依赖于cpt(ti)。如果通过填充操作消除了这两个任务之间的通信成本，则预期会有益处，因为任务ti可以更早地执行。

如果只填补目标任务cpt(ti)，就会出现问题。假设cptcpt(ti)、cpt(ti)最初运行在同一处理器上。如果ti填充cpt(ti)，则不会消除cpt(ti)和cptcpt(ti)之间的通信成本，即使它消除了ti和cpt(ti)之间的通信成本。cptcptcpt(ti)与运行在相同处理器的cptcpt(ti)存在相同的情况。

解决这个问题的方案是将整个关键前端任务链(在单个处理器上分配)视为一组目标任务。设R为目标任务集，tr为cpt(ti)。目标任务tr扩展为一组目标任务R，包括cpttr、cptcpttr等。在填充操作中，R中所有任务都被认为是填充候选。因此，填充操作中任务ti的目标任务集为R=tjl::tjm，其中对于l≤r≤m-1，存在tjm=cpt(ti)，φcpt(ti)≠φ(ti)，tjr=cpttjr+1，φtjr≠φtjr+1。

在填充过程中，只有在通过可行性检查和新的时间表是可接受的情况下才执行填充操作。如果当前堆栈R的可行性和可接受性检查失败，则移除堆栈R的顶部并重复该过程，直到通过检查或堆栈变空。整个过程如算法3所示。

算法3： 填充操作

(1)N←T中任务的拓扑排序列表；

(2) whileN≠∅ do

(3) 选取N中的第一个任务tk；

(4) 寻找满足填充条件的tk,R对；

(5) whileR≠∅ do

(6) if 插入R可行 then

(7)ψ′←Pull_optk,Rψ；

(8) ifψ′可接受 then

(9)ψ←ψ′， 跳转步骤(2)；

(10) 移除R的最顶端；

(11) endwhile

(12)R←R-tk；

(13) endwhile

3 实验分析

3.1 实验设置

所使用的调度算法在公共计算平台上进行了仿真：CPU双核英特尔Xeon(3.0 GHz)服务器PC，内存为6 GB ddr4-2400k，系统为win7旗舰。两个基于列表的启发式算法，异质性最早完成时间算法(HEFT)和异质性关键父树算法(HCPT)，被用作基线算法，因为它们是迄今为止针对异构系统提出的性能最好的算法之一。两种算法实现过程如图4所示。

图4 HEFT和HCPT实现过程

考虑图4所示示例，为一个简单的DAG和一个由两个处理器组成的计算系统，两个处理器通过一个链路相连。当使用HEFT算法时，生成的调度如图4(a)所示。该算法根据任务优先级形成一个任务序列，然后按顺序逐个分配给处理器。当使用HEFT算法时，生成的调度如图4(b)所示。该算法根据任务优先级形成一个关键父树任务序列，然后按照父树子树模式逐个分配给处理器。

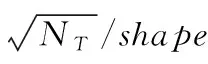
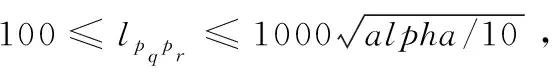
表1 参数值集

使用参数值集的所有组合(总共11 520个测试用例)来创建应用程序DAG模型G和异构集群图模型HC。相对于最小关键路径SLR的调度长度是用于评估DAG调度算法的常用性能度量。然而，由于推送-填充算法被设计用于提高由基线算法生成的调度完整性，所以另一个性能度量，改进SLR，也用于评估考虑的调度算法[15,16]

(5)

式中：SLRBA是基线算法产生调度方案的关键路径SLR，SLRGSA是使用引导搜索算法产生的调度方案的关键路径SLR。

3.2 结果分析

对比算法选取模拟退火(SA)[17]，禁忌搜索(Tabu)[18]，TASK算法[19]，模拟进化(SE)[20]。在SA算法中，初始温度被设定为初始计划的完工时间。下一代的解决方案是概率接受的。在Tabu算法中，试图找到更好的解决方案的跳数决定了调度开销。在SE中，控制解的搜索时间的选择偏差B设置为0。参数Y是根据特定任务在所有处理器上的执行时间分配给它的处理器数量。在设置中，Y是20，这表示只有在异构集群系统中考虑的最好的20个处理器。

在图5中，在平均和最大SLR改进方面比较几种引导搜索算法的性能。

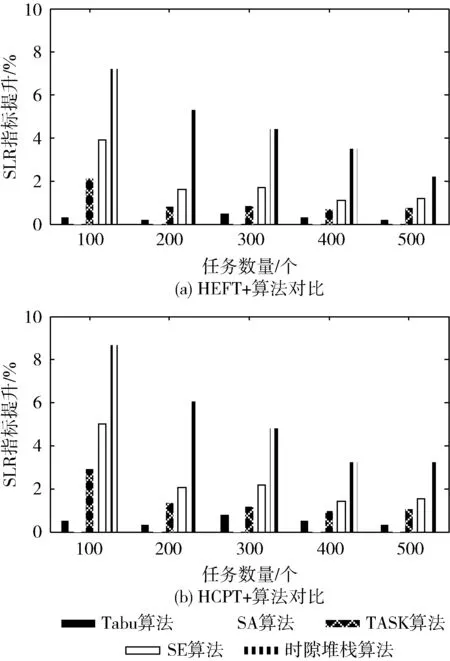
图5 作为任务数量函数的SLR改进

根据图5实验结果可知，在与选取的SA算法，Tabu算法，TASK算法以及SE算法对比实验过程中，结合异质性最早完成时间算法(HEFT)和异质性关键父树算法(HCPT)的实验对比结果分别如图5(a)～图5(b)所示。从图5(a)可以看出，在HEFT框架下，本文算法的SLR指标提升幅度显著的高于选取的SA，Tabu，TASK算法以及SE几种对比算法，这表明本文算法的最小关键路径SLR的调度长度提升幅度最高，体现了所提时隙堆栈算法在任务调度算法上的有效性。以上分析结果同样适用于HCPT框架下的实验对比分析结果，上述结果验证了所提算法的有效性。

选取HEFT作为基线算法，利用其它参数值获得的性能结果趋势如图6所示。

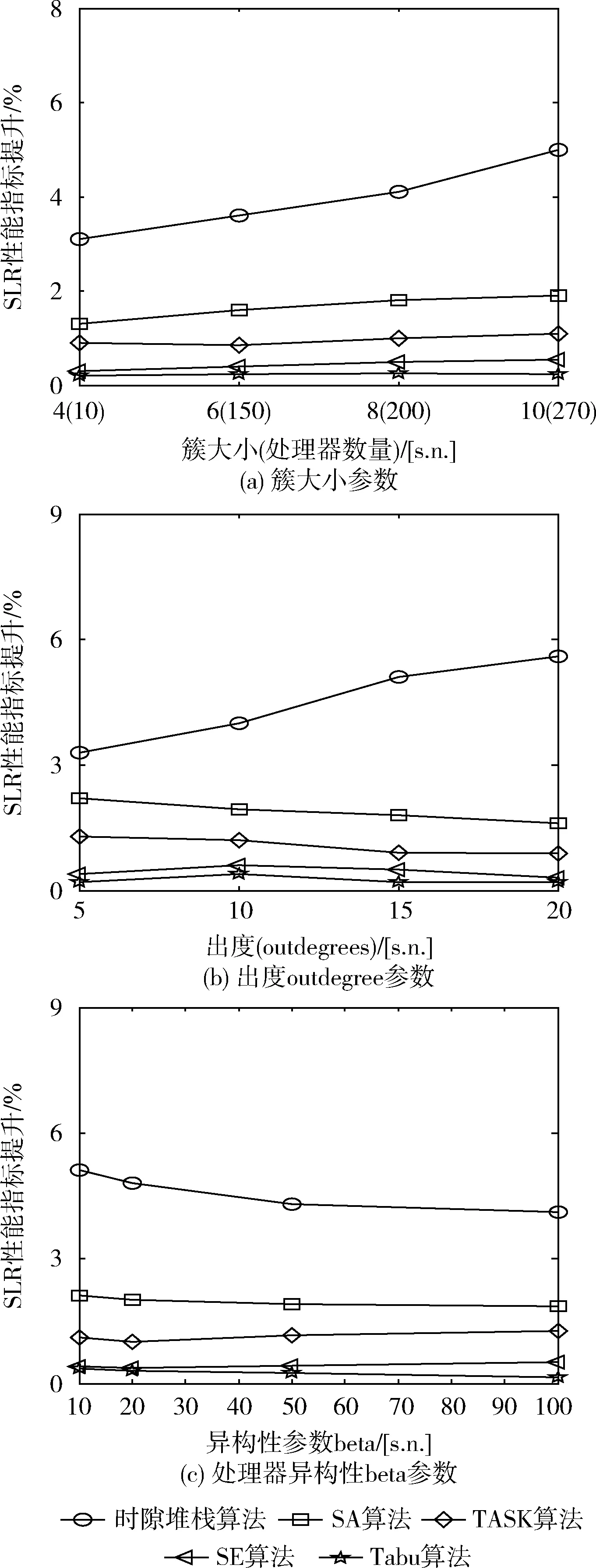
图6 度量指标SLR改进效果对比

根据图6结果可知，SA算法、Tabu算法、TASK算法、SE算法以及本文算法的SLR指标提升幅度均随着簇大小参数的增加，这表明增加簇大小参数有助于SLR改进得到提升，因为存在更多的处理器导致更多的机会增加并行性。在图6(b)中，随着出度outdegree参数增加，所提算法SLR指标提升幅度增加，大大优于其它算法，而选取的对比算法在出度outdegree参数增加后均出现下降趋势，这是因为对比算法并未考虑出度outdegree参数的优化问题，而本文算法在设计过程中考虑到了出度outdegree参数问题。这个结果暗示了所提算法在改善外延DAG的调度长度方面优于其它引导搜索算法。图6(c)中，随着异构性参数的增加，几种对比算法的SLR指标提升幅度均出现下降趋势，但是本文算法相对于选取的对比算法具有更佳的性能表现，上述实验结果验证了所提算法的有效性。

同时，为验证所提算法的计算性能优势，这里选取上述几种算法在HCPT和HEFT框架下的计算时间进行实验对比分析，结果见表2。

根据表2所示算法计算效率实验对比结果可知，在HCPT和HEFT框架下，本文算法的计算时间分别为2.13 s和3.17 s，均不高于10 s，而选取的几种对比算法在上述算法框架下的计算时间均高于10 s，相对于本文算法的计算时间均高出近4倍以上，这表明本文算法在上述算法框架下的计算效率要显著优于所选取的对比算法，主要原因是本文采用的是列表式计算方法，继承了该类算法的计算效率优势，而选取的对比计算方法采用的均是进化计算方法，具有较高的计算复杂度，上述实验结果体现了算法的计算效率优势。

表2 计算效率对比

4 结束语

针对异构集群系统，提出了一种基于引导搜索策略的静态调度算法，称为时隙堆栈算法。该算法从基线算法生成的初始解中搜索改进的解。通过在一个给定的调度计划中迭代地推送和填充任务，实现试图改进初始解的效果。该算法在改善诸如HEFT或HCPT等列表调度算法生成的初始解方面特别好，因为时隙堆栈操作修复了列表调度算法的主要缺点。最后通过实验仿真过程，对所提算法的有效性进行了验证。下一步研究，主要集中在应用系统开发以及算法理论分析两个角度，对所提算法进行深入拓展。