二维小波提升-DCT变换对地电场压缩算法

顾 涛

(华北科技学院 计算机学院，河北 燕郊 065201)

0 引 言

数据压缩是海量数据监控领域中经常要面对的问题。对于10 KV架空线路系统，其对地电场监测数据的保存是供电单位电能质量数据必须要保存的数据之一。分析已监测到的对地电场历史数据，可以得出结论，当线路正常时，其值在±15%范围内波动。当故障发生时，其值会剧烈波动，波动范围一般大于75%-95%以上。这样数据特征就比较符合利用有损压缩算法对数据进行高压缩比压缩，因为数据恢复后，其显著的变化特征不会丢失。对于电力领域内比较著名的数据压缩算法是以色列的PQZIP压缩软件采用的快速FFT压缩算法。该软件利用FFT技术实现对正弦波高速采样数据的压缩，最大压缩比可以达到1000∶1。这种基于FFT压缩算法是有损压缩技术，特别适合被压缩对象是正弦变化的波形。但对于对地电场监测值，由于是定期采样获得的有效值，其值变化受各种因素影响，不是正弦变化。因此，针对对地电场值高压缩比存储，需要研究其它压缩算法。近年来提出的压缩感知[1-5]算法已用在电能质量数据存储中，但该算法之核心还是用到DFT技术。考虑对于图像数据处理，利用二维DCT变换和二维小波分解变换可以有效的对图像进行压缩编码。二维DCT变换可以将变换后的数据非常有效地集中到矩阵左上角区域，但对于图像分块边缘效应比较明显，这是其缺点所在。图像在经过二维小波变换后，分解后的系数在低频系数矩阵、垂直系数矩阵、水平系数矩阵、对角系数矩阵中得到集中和重新分配，只要对分解后系数进行硬阈值处理，就可以有效压缩图像数据。受二维DCT和二维小波变换对图像高效率压缩启发，本文将采样得到的一维电场数据按照行顺序排列，先构造成128×128数据块，对构造的数据块做二维haar小波提升分解，再利用二维DCT变换，对小波分解系数做二次变换。通过构造二维系数筛选矩阵对DCT系数和小波系数进行筛选取舍。对筛选到的系数再进行一维小波变换编码，最后实现对原始一维数据高压缩比压缩。该算法实质是利用DCT变换进行二次系数集中，通过mask稀疏矩阵对系数软阈值化处理，再对所选系数进行一维小波变换编码。虽然用到二维DCT对小波分解块系数做变换，但该算法并不存在边缘效应。实验结果表明，采用该算法，对于正常波动的对地电场数据压缩，压缩比可以达到1024∶1，数据恢复后误差控制在8.7743%-0%。提高数据块编码尺度大小，在保证一定数据质量的情况下，压缩比还可以提高到2048∶1。

1 二维haar小波提升与二维DCT变换

Daubechies等系统地证明了所有小波变换都可以通过分解、预测、更新和尺度缩放4步提升实现[6]，使一度深奥的小波变换得到简化，极大地促进了小波理论应用[7-11]。

1.1 haar小波提升变换

利用Z变换技术，先对小波滤波器进行变换并将奇偶系数分开重组，然后再使用Euclidean算法分解，小波变换多相位矩阵P(z)最终可以用式(1)表示为

(1)

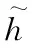
(2)

(3)

原始信号才能在分解后得到完美重构。

式(1)给出小波提升过程可以分为4个步骤即分解、预测、更新和尺度缩放。重构过程正好是其反过程。本算法使用haar小波对构造出的数据方阵做二维小波提升变换，haar小波4个滤波器分别为：

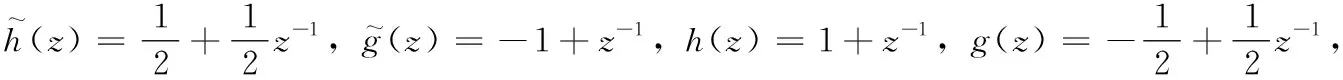
(4)

对偶多相位矩阵为

(5)

因此，haar提升过程就可以用式(6)到式(9)表示(设x是待分解信号，dl和sl分别是小波分解后的高频系数和低频系数)

(6)

(7)

(8)

(9)

根据前向提升公式，可以求出逆变换公式如下

(10)

(11)

(12)

(13)

利用haar小波对所构造的数据块做提升变换时，先对每行进行一维提升变换，然后对中间变换结果的每列再做一维提升变换，由此得到数据块二维提升变换。同样，可以利用haar逆变换公式求取二维逆提升变换结果。

1.2 二维DCT变换

本文利用64×64二维DCT变换矩阵，将二维小波变换结果再做进一步变换，使变换后数据进一步集中在左上角，利于后续数据处理。

64×64二维DCT变换和逆变换分别定义为式(14)、式(15)表示，设Amn为待变换的数据方阵，Bpq为变换后的方阵，则有二维DCT正变换

(14)

逆变换为

(15)

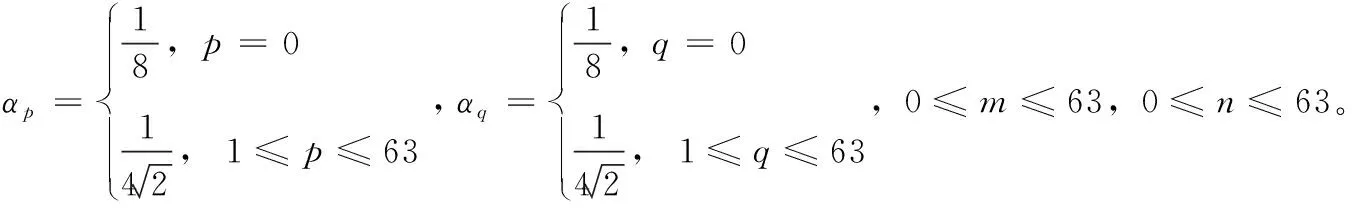
从式(14)、式(15)可知，DCT变换和IDCT变换具有线性可加性和变换核可分离性，均可以通过一维DCT、IDCT变换实现。

2 数据压缩算法

2.1 压缩步骤

10KV架空线路对地电场数据是分析接地故障重要参数之一，需要长期对其保存，供故障追溯使用。架空线路监测点众多，数据量大，需要对上传数据进行压缩保存。图1给出对地电场数据压缩具体实现步骤。第一步，先将获取的监测数据序列构造成128×128二维数据方阵A。第二步，对方阵A做二维haar提升小波变换(LWT2)，得到矩阵B。数据方阵A变换后能量重新分配在低频系数ca1矩阵、垂直系数cv1矩阵、水平系数ch1矩阵、对角系数cd1矩阵中，有利于下一步DCT变换进一步能量集中。每个小波系数矩阵行列数目均是原来数据矩阵的一半。第三步，将ca1、cv1、ch1、cd1再构造成一个128×128方阵B，再利用64×64DCT变换核，对新构造的矩阵B变换。变换后的ca1_dct2、cv1_dct2、ch1_dct2、cd1_dct2矩阵能量最后主要集中在左上角。第四步，构造MASKC64X64稀疏矩阵，对dct变换系数矩阵C进行筛选，获取筛选结果矩阵D。构造MASKC64X64矩阵时，突出筛选出能量大的和决定频率变化的数据，筛选方法是将一行数据排序，取一行中前a个最大值和后a个最小值，a和压缩比有关。第五步，对矩阵D非零数据重新排列成一维数组，利用一维haar小波提升变换和软阈值处理，进一步将数据压缩，最后获取部分压缩数据DATA1，压缩信息中不含位置信息，其元素位置信息由MASK稀疏矩阵中1的元素位置决定。

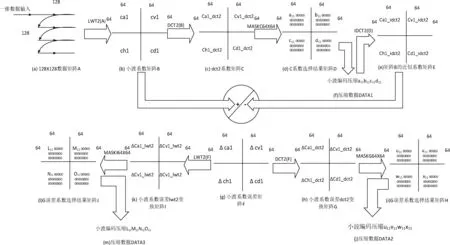
图1 一维采样数据压缩步骤

第六步，对DATA1解码，做二维DCT逆变换，得到矩阵E，此矩阵是矩阵B的近似矩阵。第七步，构造小波系数误差矩阵F，令F=B-E。第八步，对误差矩阵F做DCT2变换，得到矩阵G。第九步，构造MASKG64X64稀疏矩阵，对矩阵G系数筛选，得到矩阵H。第十步，利用一维haar小波提升变换和软阈值处理方法，将矩阵H非零元素压缩成数据DATA2。

第十一步，对误差矩阵F做LWT2变换，得到矩阵I。第十二步，构造MASKI64X64稀疏矩阵，对矩阵I系数筛选，得到矩阵J。第十三步，利用一维haar小波提升变换和软阈值处理方法，将矩阵J非零元素压缩成数据DATA3。

2.2 压缩误差系数修正

DATA1、DATA2、DATA3即是原来一维数据经过各种变换压缩的结果。从图1中，我们可以知道，小波系数矩阵B是矩阵E与矩阵F之和。要想理想恢复原压缩数据，需要将误差矩阵F求的精确。令

B=E+F

(16)

其中，E=IDCT2(ILWT(DATA1))。

同时，令

F=α(IDCT2(ILWT(DATA2)))+β(ILWT2(ILWT(DATA3)))

(17)

其中，称α为DCT误差系数调整因子，β为小波误差系数调整因子。压缩数据越少，压缩比越大，α、β越大，反之亦然。数据实验表明，α在0～3.5之间，β在0～1.5之间恢复出的数据比较理想。

B=IDCT2(ILWT(DATA1))+α(IDCT2(ILWT(DATA2)))+β(ILWT2(ILWT(DATA3)))

(18)

压缩数据时，提供给用户可调参数有压缩比。α、β参数根据压缩比，压缩算法自己计算其值。当用户调整好压缩比参数后，根据压缩比，可以计算出矩阵E、矩阵H、矩阵J中总共要保留多少参数，假设为L。按照矩阵E保留4个，矩阵H保留(L-4)/2个，剩下为矩阵J的。根据提前设定好的α、β值范围，当选定一组，做逆变换，求取最大误差，若误差满足要求，该组α、β值就是选定的值。若误差不满足，继续调整α、β值再计算，反复修订后，α、β值可以求出。整个算法中，当压缩比确定后，就可以确定每个矩阵分配多少个保留系数，由此就可以分配每行保留几个数据。3个MASK稀疏矩阵按左上角第一行第一个元素开始设置为1，该数据必须保留，其它元素初始化均为0。每行设置个数不超过行总数目的1/4(16个)，具体个数由压缩比计算决定。保留的数据要突出能量大的和影响频率的数据(极小、极大数据)，系数筛选规制按2.1节介绍内容进行。第一行设置完毕后，开始设置第二行，以此类推，对于DCT2系数筛选，第一行数据重要性远远高于第二行数据，一般设置两行即可。

3 压缩数据分析

任意取现场采集到的电场数据做第二节算法描述的数据压缩过程，考察在不同压缩比下数据解压缩后百分比误差范围，以检验压缩算法是否满足现场技术指标要求。表1中给出了5组实验数据，说明了本算法的有效性。图2到图6对比了不同压缩比下数据恢复曲线与原曲线波形差异，压缩比越高，数据波形失真越大。

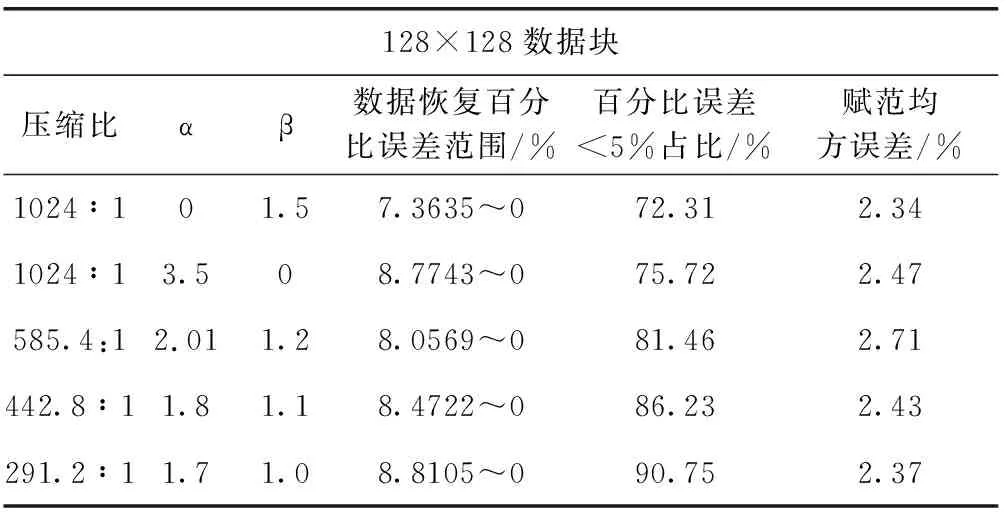
表1 不同压缩比、α、β，对应不同恢复百分比误差

注：表中压缩比定义为原始数据长度/压缩后数据长度。同时采用百分比误差范围和百分比误差占比两个指标考察压缩效果，以对应对地电场技术指标误差范围±10%要求。

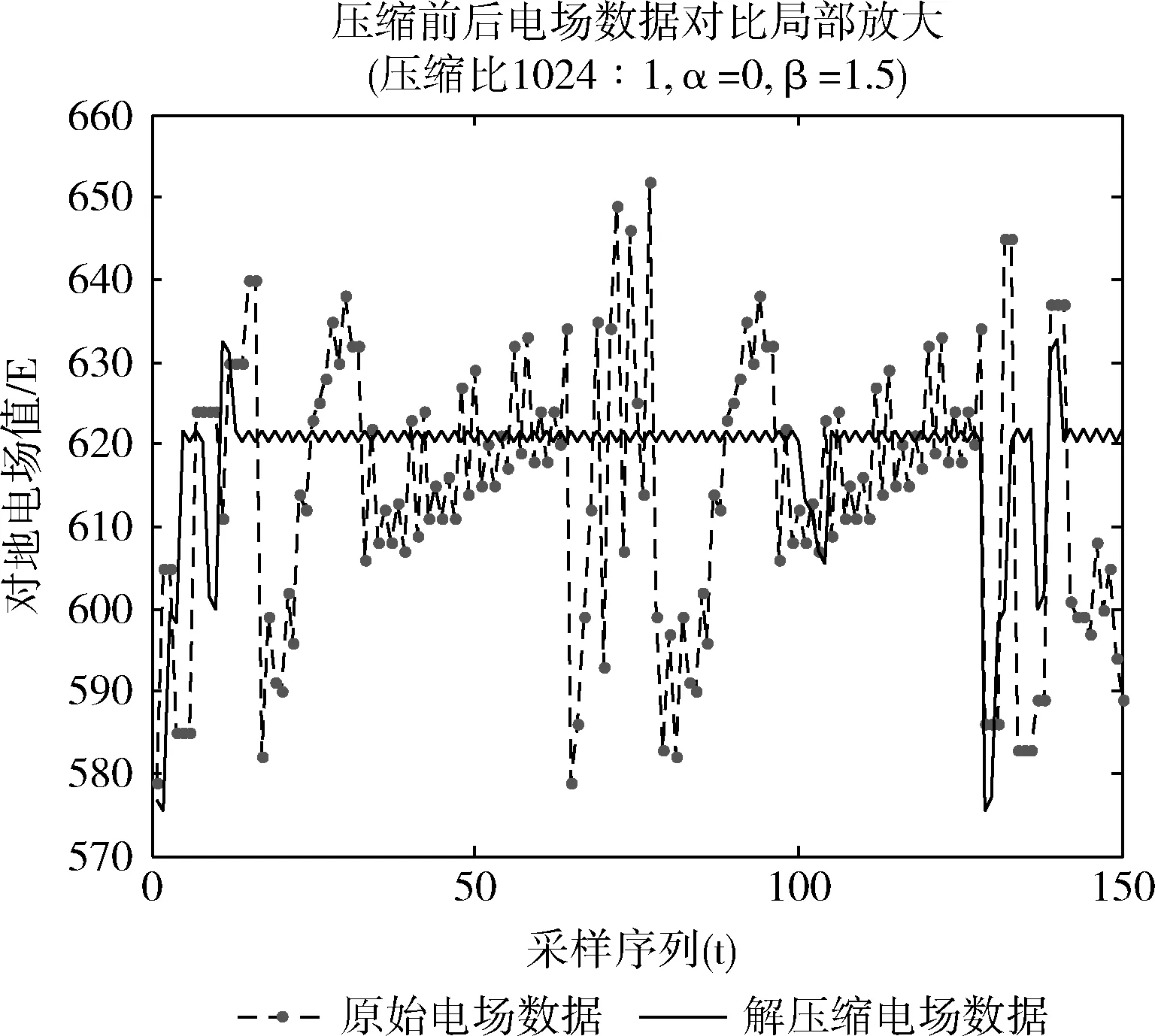
图2 lwt2(F)变换压缩后恢复曲线

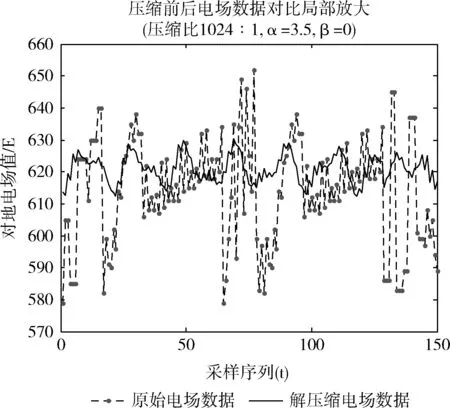
图3 dct2(F)变换压缩后恢复曲线

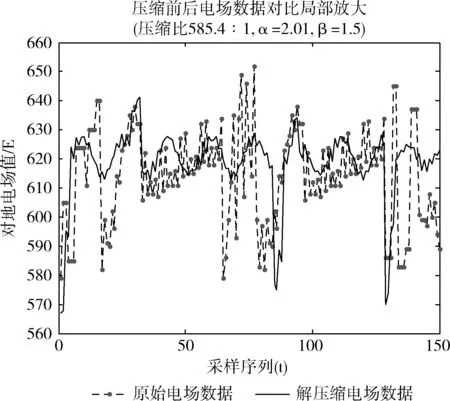
图4 lwt2(F)和dct2(F)变换压缩后修正数据恢复曲线(压缩比585.4∶1)

图5 lwt2(F)和dct2(F)变换压缩后修正数据恢复曲线(压缩比442.8∶1)

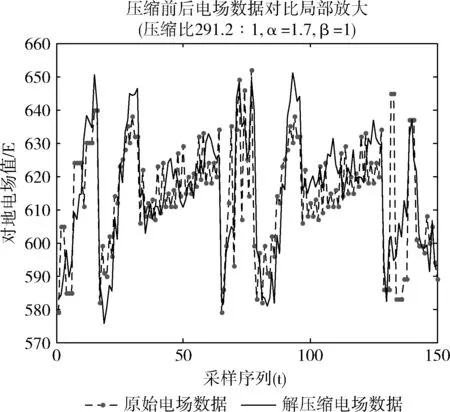
图6 lwt2(F)和dct2(F)变换压缩后修正数据恢复曲线(压缩比291.2∶1)

表1实验数据说明，随着压缩比降低，解压缩后数据百分比误差小于5%的数据占比提高，数据精度提高。不同压缩比下，数据恢复最大百分比误差小于10%，符合现场对地电场技术指标误差范围±10%要求。虽然不同压缩比下，赋范均方误差相差不大，但百分比误差<5%占比相差很大，说明本文所提指标更能刻画数据解压缩失真情况，从波形对比上看百分比误差占比指标更符合直观感受。表1中所有压缩实验结果，前提是只取了系数矩阵C中4个数据做IDCT2，其结果作为近似矩阵E，即矩阵C中每一个64×64子矩阵左上角第一行第一列之元素，可见局部压缩比高达4096∶1。

图2至图6说明，lwt2(F)变换后压缩的数据DATA3在数据恢复时，是对dct2(F)变换后压缩数据DATA2的有益补充，可以有效恢复数据曲线细节。在压缩比确定后，根据百分比误差率设置，α、β值就可以计算确定出来。图中同时给出了不同压缩比下，α、β不同取值条件下所对应的解压缩波形与原始数据波形对比。

文献[1-5]算法核心都是采用DFT变换，然后构造稀疏矩阵进行压缩。经过压缩算法比较换算后，文献[1]压缩比约为168∶1，文献[2]压缩比约为5.06∶1，文献[3]压缩比约为34.13∶1，文献[4]压缩比约为11∶1，文献[5]压缩比约为13.2∶1。与文献[1-5]相比，本算法综合压缩比性能更高。

进一步理论分析和计算表明，当矩阵D取4个数据，矩阵G取40个数据，矩阵I取64×16个数据，对于任意对地电场128×128数据块，此时压缩比在15.34∶1左右，压缩数据即可得到较完美恢复。与PQZIP压缩正弦信号相比，该算法能提供非正弦信号高压缩比压缩。本算法性能在matlab R2016b平台编程得到验证。α、β参数设置由压缩比确定后，压缩算法根据误差率自适应计算其值。

4 结束语

提出采用二维小波提升-DCT变换算法压缩对地电场采样值，并构造误差系数矩阵F，利用不同压缩比下调整α、β因子，以提高数据解压缩恢复效果。数据压缩实验分析表明，采用本算法能够实现对地电场数据的高压缩存储，数据解压缩最大百分比误差满足现场技术指标要求。算法适合非正弦信号数据压缩，使用范围更广。算法压缩比高于基于压缩感知算法的数据压缩技术。