基于改进四叉树的ORB特征均匀分布算法

姚晋晋，张鹏超，王 彦，罗朝阳，李海婷

(1.陕西理工大学 机械工程学院，陕西 汉中 723000；2．陕西理工大学 陕西省工业自动化重点实验室，陕西 汉中 723000；3．陕西理工大学 电气工程学院，陕西 汉中 723000)

0 引 言

同步定位与构图(simultaneous localization and mapping，SLAM)作为一项机器人底层技术，需要通过传感器对周围环境进行感知的同时完成对自身的定位，是机器人领域一个重要的研究方向[1]。视觉SLAM的前端根据视觉传感器信息粗略估计相机运动，其中基于特征法的前端对于特征提取的均匀度和提取效率有极强的依赖，使得特征提取成为当前视觉SLAM算法的研究热点。

传统ORB(oriented FAST and rotated BRIEF)特征提取算法已经在SLAM系统中得到广泛应用[1]，虽然可以满足SLAM系统对于实时性的要求，但是ORB特征点在图像平面仍然分布不均匀，容易出现聚集现象，降低了后续特征匹配与位姿估计的精度，为此Mur-Arta等[2,3]在ORB-SLAM系统中提出用四叉树来提高特征分布的均匀度，明显改善了特征点的均匀度，但是提取时间明显增加；禹鑫燚等[4]在此基础上对其进行改进提出了Qtree_ORB算法，有效地剔除了冗余的特征点，但仍采用传统的四叉树结构，计算效率有待提高；范新南等[5]提出一种自适应角点阈值提取方法，但是仍然含有人工设定的参数，无法真正达到自适应提取。

故本文针对以上研究者所用方法的缺点，提出一种基于改进四叉树的ORB特征均匀分布算法，在提取特征点时考虑图像的整体对比度，并且根据不同金字塔层设定四叉树的深度，从而减少冗余特征点的计算，提高特征提取的效率。

1 传统ORB算法

传统ORB算法主要包括两个步骤，FAST角点检测和Rotated BRIEF描述子计算。其中FAST算法通过选定元素与周围元素像素灰度的差值来检测角点。文献[2]采用FAST-9算法，以像素p为例，在以p为中心半径为3个像素的圆上共有16个像素点，如果这16个像素中有连续9个像素与p的灰度差值大于设定阈值t，则判定p为FAST角点。计算如式(1)所示

(1)

其中，I(x) 为圆周上任意一点的像素值，I(p) 是待检测的像素灰度值，t为角点检测阈值，FAST-9中N=9。此外，为了剔除边缘点，采用Harris响应值取代FAST响应值，并且为了提高特征的鲁棒性，通过构建金字塔实现尺度不变性，为特征点添加了主方向实现了旋转不变性，为了避免角点集中问题，采用非极大值抑制对其进行一次筛选[4]。对于其特征点方向的计算具体如下：

(1)在一个图像块中，定义图像块的矩为

(2)

其中，I(x,y) 是图像灰度。

(2)通过矩找到图像块的质心

(3)

θ=arctan(m01/m10)

(4)

对于特征点的描述采用Rotation BFIEF，它是一种二进制描述子，其描述向量由多个0和1组成，文献[2]中采用256维向量对角点进行描述，并且做了平滑处理，在特征点附近31×31的像素区域内用5×5的子窗口的灰度值之和作为判断描述子的依据，得到描述子分段函数，具体计算如式(5)所示

(5)

其中，p(x)、p(y) 分别为点x和点y处的像素灰度值，τ即为描述子的值，x和y处的灰度值即上述子窗口的灰度值之和。此外将式(4)中计算的方向加入到描述子中，使得描述子具有良好的旋转不变性。

2 基于改进四叉树的ORB特征提取

改进算法首先针对FAST角点提取抗干扰能力差的问题，根据不同图像的灰度值计算来代替人工设定值；其次在Mur-Arta[2，3]提出的方法上，根据不同的金字塔层为四叉树加入不同的深度检测，以限制四叉树过度分割，减少冗余特征计算，从而提高算法的计算效率。算法结构如图1所示。

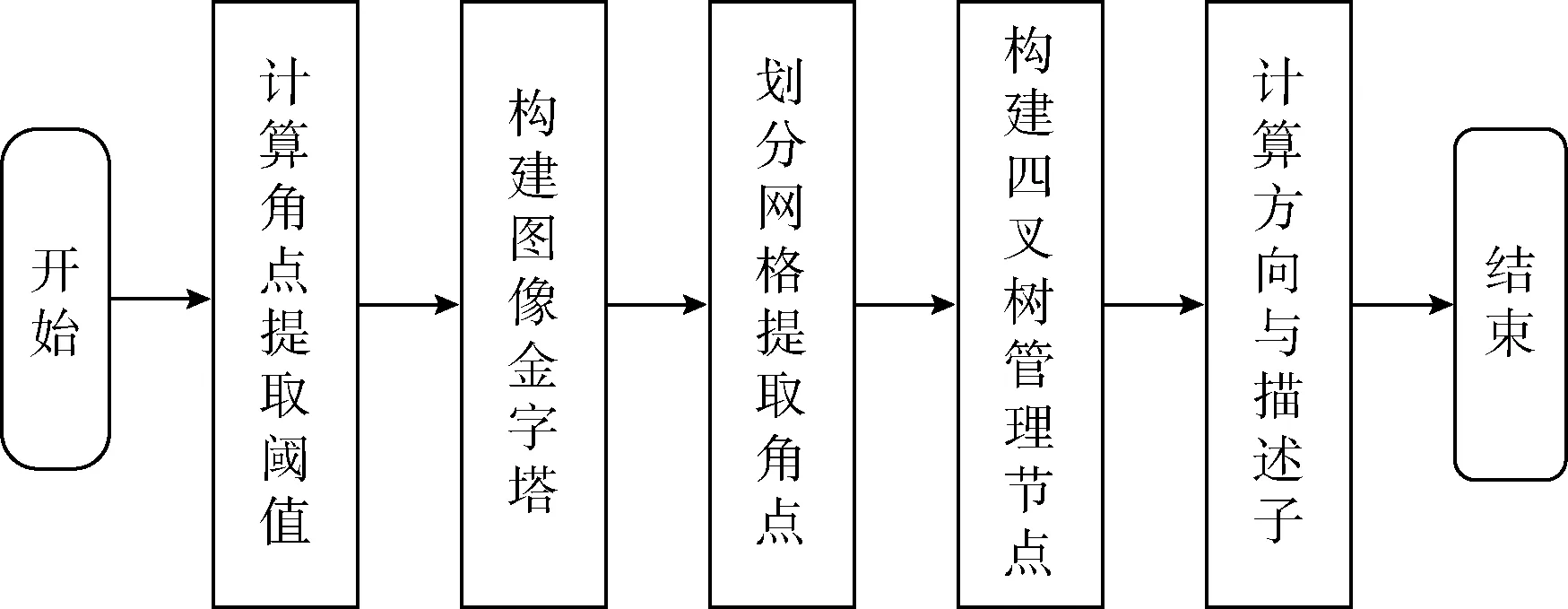
图1 算法结构

(1)对于FAST角点的提取是根据待检测像素与周围像素的灰度差进行的，但是比较阈值无论是传统算法还是后续Mur-Arta等提出的算法均是人工设定的，并没有考虑图像自身的全局信息，而范新南等[5]提出的自适应阈值中仍然含有人工设定的比例因子，本文算法根据图像灰度信息计算出一种不同的自适应阈值用于FAST角点检测，计算方法如式(6)所示

(6)

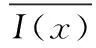
(2)图像金字塔，为了使ORB特征具有尺度不变性，为图像构建了八层金字塔，同时按照比例因子计算每一层所需的期望特征点数量。记所需特征点总数为m，尺度因子为s，第1层所需特征数为a，则有

(7)

(3)划分网格提取FAST角点，为了使角点均匀分布在整个图像，对图像进行网格划分，初始化网格为边长为30像素的正方形，然后根据图像的分辨率计算出分割出的行数L与列数R，由于图像并非正方形而是矩形，所以再根据所计算的行数与列数计算网格的宽和高。以计算网格的宽为例，图像的宽为width，则分割的列数为

R=width/30

(8)

再由列数求出实际网格宽

w=round(width/R)

(9)

其中，w为最终网格的宽，round()的作用是对函数结果取整，实践验证以30像素为初始化边长可以满足提取点数量的要求且具有较高的计算效率。

划分网格完成后采用第(1)步计算所得的iniT作为初始提取阈值进行角点提取，如果该网格内没有提取到角点，就降低阈值为minT=iniT/4， 继续在网格内进行角点提取，直到遍历图像中的所有网格，通过该方法完成角点的粗提取，使得图像的每个网格中都存在角点。

(4)构建四叉树，通过第(3)步所得的角点存在大量的冗余，需要四叉树对其进行进一步的筛选。四叉树的思想是将数据区域分为4个象限，在特征点的筛选中，首先设定初始化节点为整张图片，得到的原始四叉树节点，之后在每个节点中检测角点的数量，如果大于1，则继续分裂子节点，如果等于1，则不再分裂并将该节点存储；当节点数量到达期望特征点数量时，四叉树分裂完成，不再继续分裂。

但上述步骤中由于没有对四叉树深度进行限制，造成分割次数过多，降低了算法的计算效率，本文在此基础上根据不同金字塔层的期望特征点数设置不同的深度，以提取500个特征为例，第一层最大深度设置为5即可满足要求，而第8层最大深度设置为3即可，不同金字塔层不同深度的设计有助于减少冗余特征的计算，从而提高计算效率，具体算法流程如图2所示。

图2 改进四叉树节点管理

图2中，d为当前四叉树深度，Dmax为该金字塔层设定最大深度，Num_kp为节点中特征点的数量，Num_j为存储节点数量，Set_Kp为该层期望特征点数。最大深度与该层节点数量关系如式(10)所示

4Dmax≥Num_j

(10)

(5)计算特征点的方向与描述子，本文仍然采用传统的计算方法，在此不再赘述。

3 实验结果

本实验在Ubuntu16.04 LTS操作系统上进行，计算机CPU为i5-4258U，8 GB内存，通过在不同数据集上的测试检验特征均匀度与计算效率。

为了量化均匀度，采用以下计算方法[8]。首先从竖直、水平、45°和135°这4个方向以及中心和外围对图像进行区域划分，得到了上、下、左、右、左上、右下、右上、左下、中心和外围10个区域；接着统计出每个区域内的特征点的数目，并根据这些数据计算出改组数据的方差V，最后均匀度u计算公式为

u=101log(V)

(11)

该数值越小，则不同区域内的特征点数量差别越小，分布均匀度越好。

为了验证该算法对于提高均匀度和计算效率上的有效性，以及对于不同条件下的适应性，采用K.Mikolajczyk和C.Schmid创建的数据库中的图像进行验证[5]，该数据库中包含不同分辨率，不同模糊程度，不同视角以及不同亮度的图像，本文采用其中的5组数据集，其中bike数据集是一组不同模糊程度的图像，leuven数据集是一组不同对比度的图像，bark是一组背景单一且占用较多幅面的图像，trees是一组前景复杂且占用较多幅面的图像，ubc是一组不同压缩度的图像，在这些数据集中，分别采用传统ORB算法、Mur-Arta在ORB_SLAM中提出的特征提取算法以及本文算法进行对比实验，并且为不失一般性，对于每组数据集均进行30次实验，以平均值作为实验结果。

图3为3种ORB特征提取算法对同一图片的提取500个特征点的结果，图3(a)为传统ORB算法的提取结果，实验采用OpenCV3.4.1中的ORB算法作为传统提取算法，图3(b)采用Mur-Arta等改进的ORB提取算法，图3(c)采用本文改进的ORB特征提取算法，图中不同大小的圆为提取的特征点，可以看到传统ORB算法所提取到的特征分布极不均匀，集中在车身和门框等区域内，而Mur-Arta的算法与本文算法所提取的特征均匀分布于整个图像。3种算法对于bike数据集的实验结果见表1，表1中MA算法为Mur-Arta算法的简写。

为了量化特征的分布情况，实验采用分布均匀度函数[8]进行计算，均匀度的数值越小，均匀分布的效果越好，并为了检验算法对于计算效率的提升，同时计算了提取特征所需时间。3种算法在bike数据集下的均匀度与提取时间实验结果见表1。由表1分析可知，Mur-Arta的算法与本文算法均对特征的均匀度有较大的提高，而Mur-Arta算法与本文算法在分布均匀度上的差距不大，最大相差约2%；同时在提取时间上，本文算法与Mur-Arta算法均比传统算法多，这是因为这两种算法均加入了四叉树对特征点的管理，但是本文算法比Mur-Arta算法耗时明显减少，平均减少时间12.12%。

图3 不同算法对bike数据集中img1的特征提取结果

为了验证本文算法对于不同光照条件的适应性，在数据集leuven上进行了测试，分别计算了3种算法在不同明暗条件下的特征均匀度与提取时间，实验结果如图4和表2所示。

图4分别为本文算法在数据集leuven上6张图像的特征提取结果，结果表明即使在明暗差距较大的情况下，本文算法仍然能够取得良好的特征均匀化效果，具体均匀度与提取时间见表2。

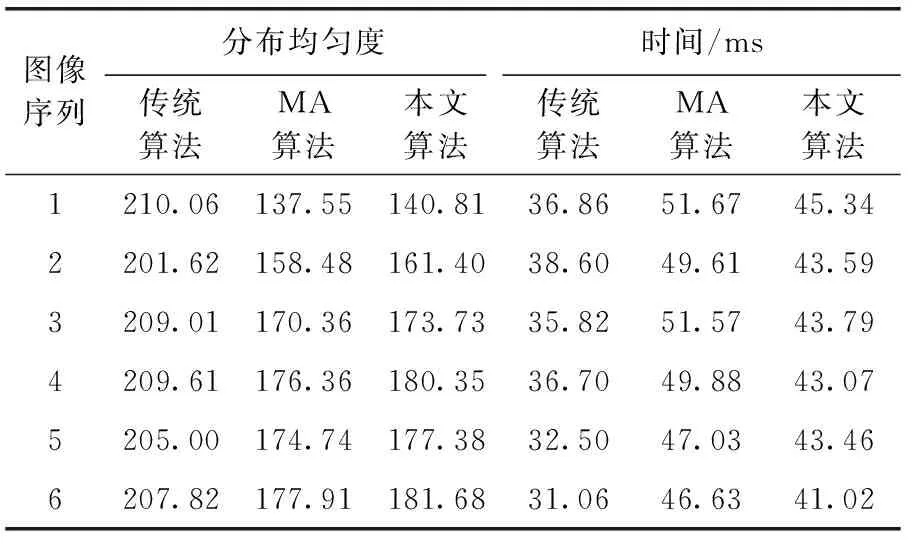
表1 3种算法均匀度与耗时比较

图4 本文算法在leuven上的特征提取结果

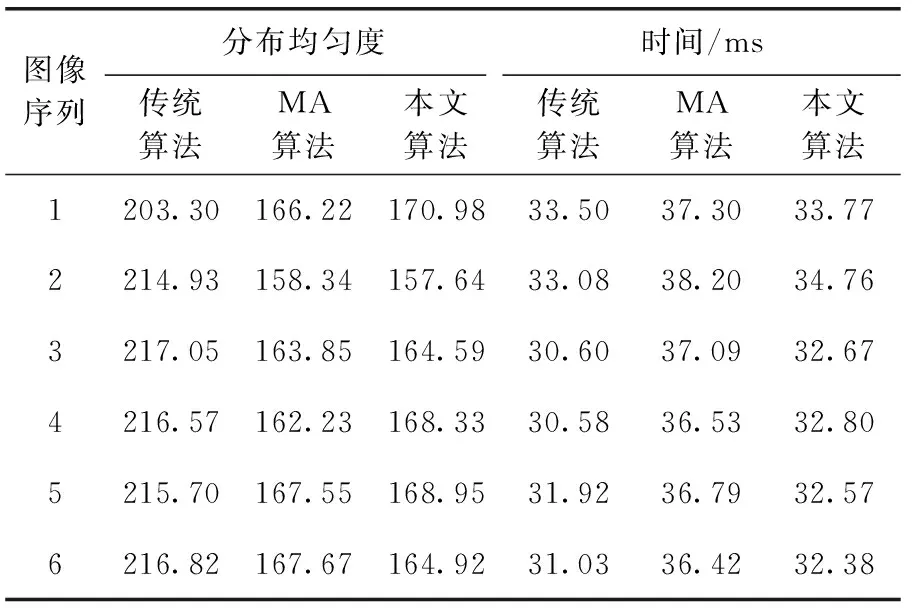
表2 3种算法在leuven上的均匀度与耗时比较

从表2可以看出，本文算法在特征分布均匀度上与MA算法相差无几，但是在耗时上有明显减少，平均减少时间10.43%，并且由于FAST角点的提取阈值是根据图像信息计算所得，所以算法对于不同对比度的图像抗干扰能力更强。

其余组的数据如图5和图6所示。图中横坐标为不同数据集的图像序号，图5为不同数据集下3种算法的均匀度实验结果，图6为不同数据集下3种算法的特征提取时间结果。

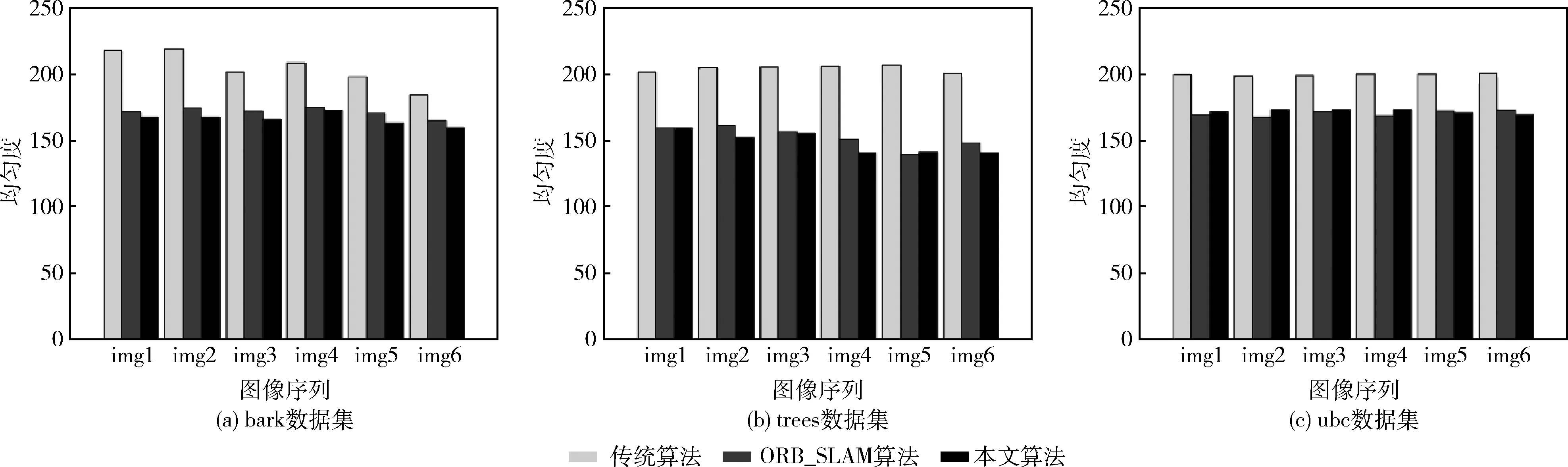
图5 3种算法在不同数据集下均匀度对比

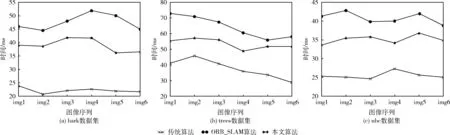
图6 3种算法在不同数据集上提取时间对比

如图5所示，在3种不同的数据集下，Mur-Arta的算法与本文算法在均匀度的表现上相差无几，并且均大幅优于传统的ORB特征提取算法，但是本文算法在背景复杂且占用较大幅面的bark数据集中，均匀度计算结果均略优于Mur-Arta的算法，在前景复杂且占用图像较多幅面的trees数据集中，本文算法的均匀度亦略优于Mur-Arta的算法，而在ubc数据集下的实验结果则没有明显的优势，两种算法在处理压缩度较高的图像时均匀度相差不大。

由图6分析可得，3种不同的数据集下，传统ORB特征提取算法的提取时间最快，而Mur-Arta的算法以及本文算法的提取时间均高于传统ORB算法，后两者的耗时主要是因为提高均匀度而做的计算。更重要的是本文算法相对于使用广泛的Mur-Arta的算法在提取时间上有大幅提高，在bark数据集下本文算法提取时间比Mur-Arta平均减少18.10%，在trees数据集下平均减少时间16.73%，在ubc数据集下平均减少时间16.30%，提取效率大幅提高。

综合以上实验数据，本文所提出的ORB特征提取算法在不同背景、不同模糊程度、不同光照以及不同压缩程度的条件下，特征均匀度和提取时间上均有更为优越的表现。

4 结束语

针对传统ORB算法分布不均、聚集现象明显的问题，提出一种基于改进四叉树的ORB特征提取算法，解决了FAST角点的自适应提取阈值选择问题，并针对不同金字塔层所需的期望特征点数设置每层的四叉树深度，最后选取多组公开数据集进行实验验证。实验结果表明，该算法相对于传统ORB算法均匀度有明显提高，并且比Mur-Arta提出的算法具有更高的计算效率，由于对不同金字塔层增加了自适应深度检测，减少了冗余特征点的计算，特征提取时间平均减少10%以上，对SLAM后续特征匹配和位姿估计都具有一定的应用价值。