复式海堤上规则波和不规则波越浪数值模拟研究
董 志,关大玮,苗 青,黄元中,张从联
(1. 广东省水利水电科学研究院 广东省水动力学应用研究重点实验室,广州 510635;2. 河口水利技术国家地方联合工程实验室,广州 510635)
0 引 言
由于越浪过程的复杂性,以往研究大多采用物理模型试验的方法。美国的Saville(1955,1958)[1,2]基于规则波越浪模型试验,提出平均越浪量计算公式,成果经整理后编入《海岸防护手册》;日本的合田良实(1983)[3]根据不规则波模型实验及越浪计算成果绘制了越浪量推算表,查表可得直立式海堤越浪量;荷兰的Van der Meer(2002)[4]对斜坡堤越浪量进行了大量研究,提出的越浪量计算公式被广泛应用。王红等(1996)[5]等通过试验分析了影响单坡堤上不规则波越浪量的主要物理因素,范红霞(2006)[6]对斜坡式海堤越浪量及越浪流进行了系统的试验研究,陈国平等(2010)[7]研究不规则波作用下海堤越浪量并提出计算公式。江洧等(2010)[8]通过物理模型试验,系统研究了不规则波作用下复式海堤越浪,提出的计算公式应用于《海堤工程设计规范》(GB/T 51015-2014)[9]。
近年来,依托传统实验方法,海堤越浪研究取得丰硕成果。但物理模型耗时费力,成本高周期长,不利于进一步研究。数值模拟手段越来越多地应用于海堤越浪研究。基于RANS方程和VOF方法,周勤俊等(2005)[10]对规则波的海堤越浪过程进行了数值模拟;张九山等(2006)[11]模拟了斜坡堤坡面上铺设异形块体情况下的越浪过程;曾婧扬等(2013)[12]对孤立波在简单斜坡堤上的越浪过程进行了模拟。张娜,邹国良(2015)[13]基于含非静水压力梯度项的非线性浅水方程,模拟了规则波和不规则波在斜坡上的波浪传播变形;李东洋等(2018)[14]基于OpenFOAM,研究正向入射不规则波与扭王块体护面斜坡堤的相互作用;王键等(2018)[15]基于Fluent软件,研究不规则波作用下带胸墙斜坡堤越浪。相比之下,数值模拟方法能节省人力成本缩短实验周期,并采集到更多实验细节数据。总体来看,这些研究多基于规则波和斜坡堤,对不规则波作用下复式海堤越浪的数值模拟研究相对较少。
本文利用CFD商业软件Flow-3D,针对两段式和三段式两类典型复式海堤,开展规则波和不规则越浪研究,分析波浪与海堤相互作用过程,并利用物模试验成果进行验证,为模型下一步应用于工程实际奠定基础。
1 数学模型
1.1 模型方法
本文选用Flow-3D的单流体模型,基于黏性不可压缩流体的RANS方程,采用VOF方法捕捉自由液面,应用RNGk-ε模型模拟湍流,利用有限差分法和GMRES算法离散和求解微分方程组。
数值造波方法采用造波边界条件法。其中,规则波根据波浪理论的适用范围,选取Sokes五阶波或椭余波作为入射波;不规则波选取JONSWAP谱作为入射波。JONSWAP谱表达式为:
盛爱萍教授对瓯越语的相关研究成果进行了梳理和归纳,在前人未曾涉及的领域进行了大胆的摸索和探讨,在此基础上进行了新的研究并有所创新。因此,使得该书立论基础厚实,其对瓯越语语汇的研究具有开拓性和前沿性,具有很高的学术价值和研究意义。
(1)
式中:α为无因次风区的函数;γ为谱峰升高因子,取值为3.3;谱峰角频率ωm=2π/Tm;σ为峰形系数:
σ=0.07,ω≤ωm
σ=0.09,ω≥ωm
(2)
为避免出口端波浪反射,采用多孔介质结合辐射边界的数值消波技术[16,17],以缩短计算域长度,提高计算效率。
1.2 造波质量分析
建立立面二维数值波浪水槽进行造波质量验证,规则波水槽示意如图1所示。其中,波浪沿X正向传播,Z向为竖直方向,Y方向为侧向(该方向只划分一个网格)。边界条件定义如下:Xmin为波浪入射边界,Xmax为自由出流即辐射边界条件;Zmin为壁面边界,Zmax、Ymin、Ymax均为对称边界条件。不规则波水槽边界条件与此相同。
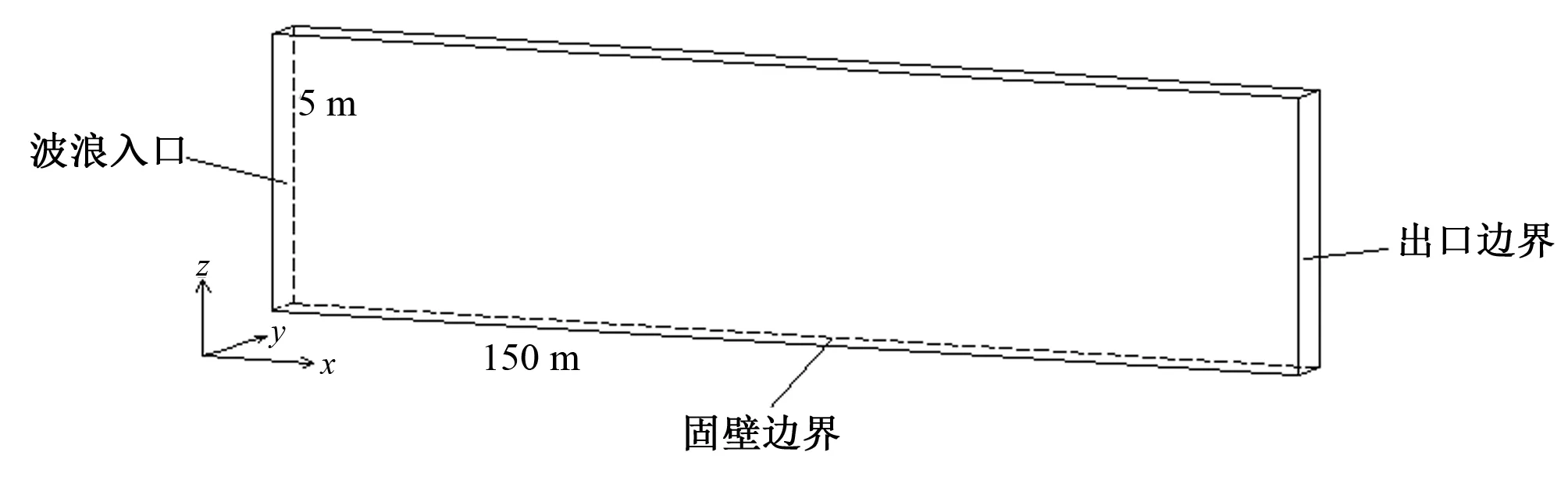
图1 规则波数值水槽布置示意Fig.1 Sketch of the numerical flume for the regular wave
对于规则波,水槽长150 m,高5 m。初始静水深为3 m,在静水面上下各1 m范围内进行网格加密,共划分221 647个网格。入射波高为0.95 m,波周期为4.73 s。对于不规则波,水槽长60 m,高1 m。入射不规则波有效波高HS=0.079 2 m,谱峰周期Tm=0.99 s。
分别将规则波和不规则波的模拟结果与理论值进行对比,如图2所示。其中,图2(a)将模拟得到的t=40 s时波面与Stokes五阶理论解进行对比;图2(b)将模拟生成的不规则波通过时域与频域的转换后,所得的波谱与理论靶谱进行比较。由图可知,数值解均与理论解吻合较好,说明规则波和不规则波造波质量较好,采用的波浪模拟方法可行且具有较高的准确性,可用以开展越浪模拟研究。
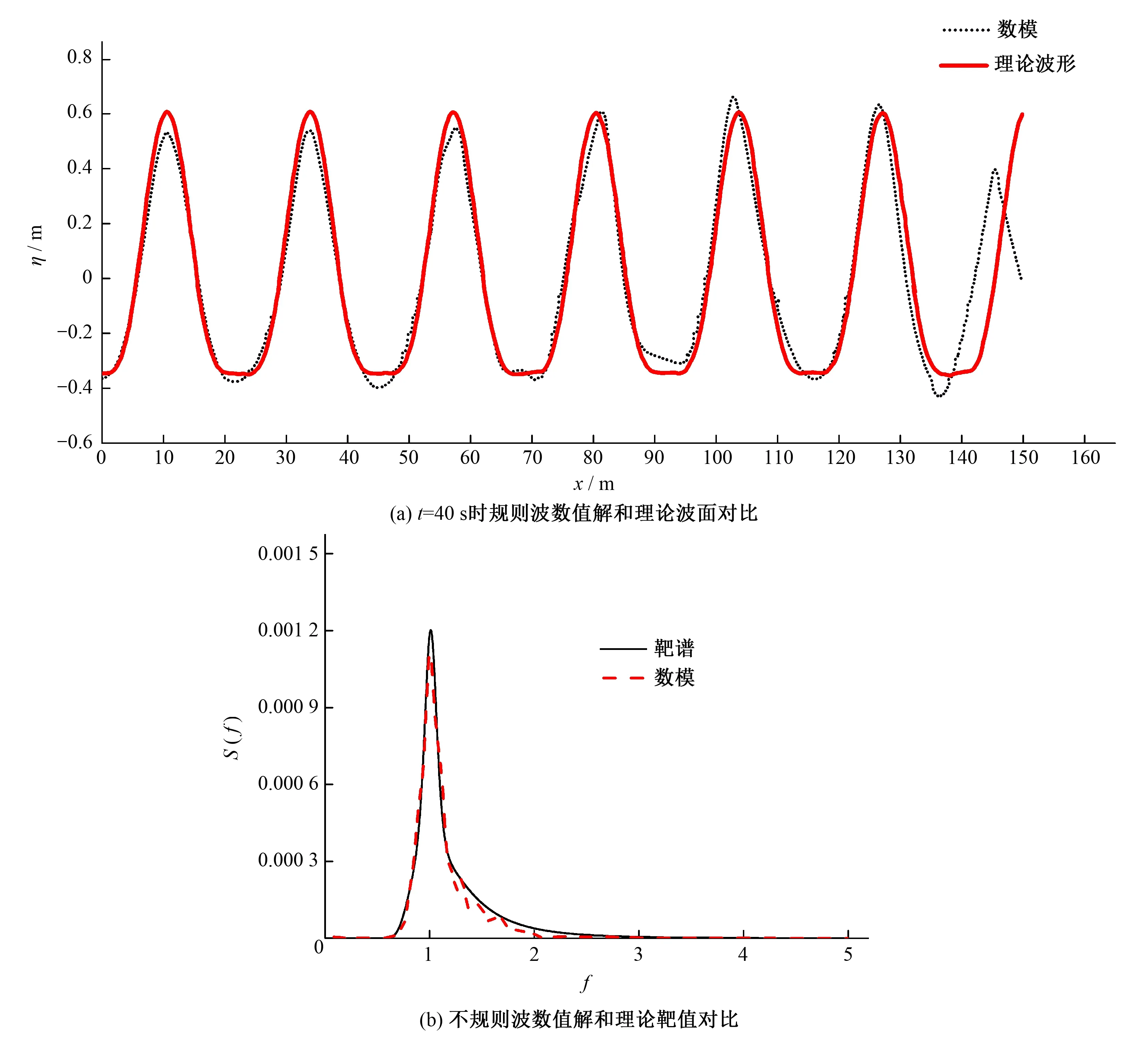
图2 数值结果与理论解比较Fig.2 Comparison of numerical results and analytical solutions
2 规则波越浪模拟
2.1 模型布置
Saville(1955)[1]利用物理模型试验手段,对两段式内折坡海堤的规则波越浪进行了研究,图3(a)是该试验所采用的海堤形状示意图。
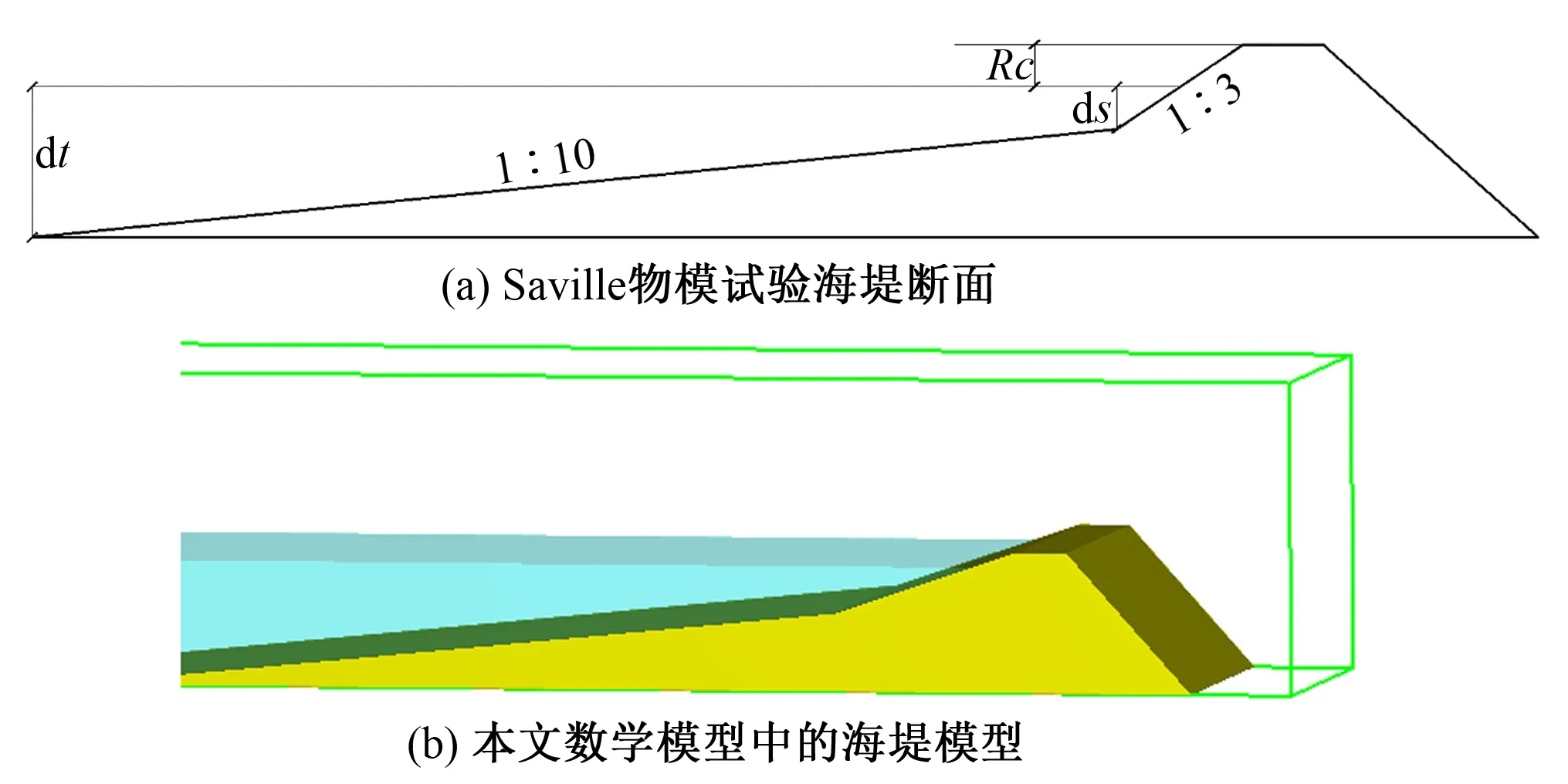
图3 规则波越浪海堤模型示意Fig.3 Sketch of the numerical model for the regular wave overtopping
本文选取该试验10组工况,开展模拟和验证工作。其中,海堤下坡坡度1∶10,上坡坡度1∶3。海堤其他参数及入射波参数包括折坡点水深ds、堤顶超高Rc、堤前水深dt,波高Ht、波周期T等,取值如表1所示。
数学模型计算域全长220 m、宽10 m、高10 m,网格总数为880万个。其中,对于静水面附近1个波高范围内的区域,进行网格加密处理。由于该模拟中规则波越过海堤后不会对海堤前方水域产生影响,计算域末端未设置消波结构,且将末端边界设为壁面边界条件。图3(b)是海堤模型附近的计算域示意图。
2.2 模拟结果验证
经模型计算后获得规则波越浪过程,以工况10为例,越浪流量过程线如图4所示。
为便于与试验成果对比,将越浪量进行无量纲化处理。其中,无量纲单宽越浪量Q的计算公式如式(3)所示。
(3)
式中:b为水槽宽度,本例中取10 m;H0为堤脚处的入射波高Ht转换前的浅水波高。对于工况1~4以及工况8~10,H0为1 m;对于工况5~7,H0则为2 m。Q0为时均越浪量,计算公式如式(4)所示。
(4)
式中:Q′(t)为统计时间段越浪流量过程;t0、t1分别为统计时段始末时刻。
越浪的数值模拟结果统计如表1和图5所示,其中除列出文献[1]的物模实验结果外,还加入Hu等(2000)[18]基于非线性浅水方程的模拟结果进行对比。
由表1和图5可知,本次模拟中工况1~8的计算结果与物模结果较为吻合,工况9、10误差相对较大,但越浪量随不同工况、不同计算参数变化的趋势基本吻合。综合来看,本次模拟计算结果相对文献[18]的计算结果偏大,但总体上与文献[1]的物模结果更加接近。
由模拟结果可以看出,在堤前水深、入射波参数相同的条件下,堤顶超高越高则越浪量越小,折坡点水深对越浪影响较小;在海堤型式相同的条件下,越浪量与入射波波高正相关。

图4 典型越浪过程模拟结果(工况10)Fig.4 Numerical results of typical overtopping processes (Case 10)
3 不规则波越浪模拟
3.1 模型布置
广东省水动力学应用研究重点实验室开展了复式海堤上不规则波越浪物理模型试验[8],部分试验成果已应用于《海堤工程设计规范》(GB/T 51015-2014)[9]等规程规范。本文的模拟方案基于本实验各工况制定。
物模试验在长66 m、宽1.0 m、高1.6 m的波浪水槽中进行,数学模型根据物理模型布置,如图6所示。其中,为减少波浪二次反射,利用薄板将水槽一分为二,海堤模型放置在其中一个隔槽中。这种分割式水槽虽增加模型计算量,但可减少波浪二次反射,同时还具有保持水槽水位恒定的作用。
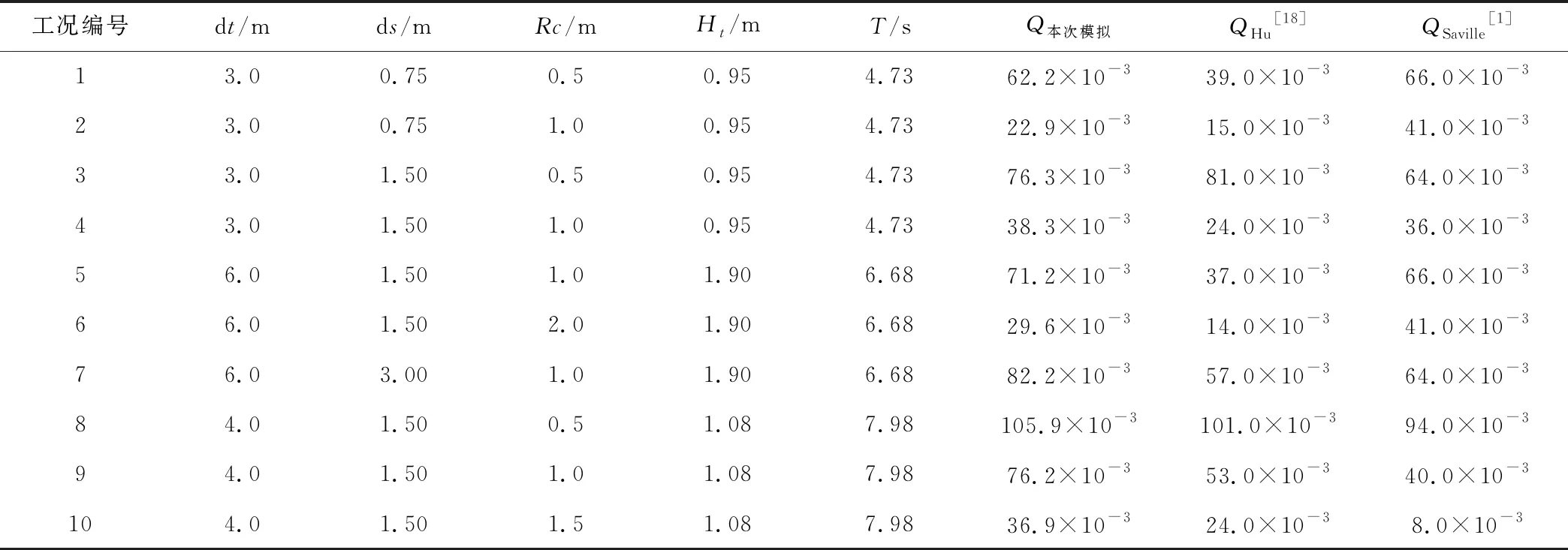
表1 各工况参数及模拟结果对比Tab.1 Comparison of case parameters and simulation results for overtopping discharge
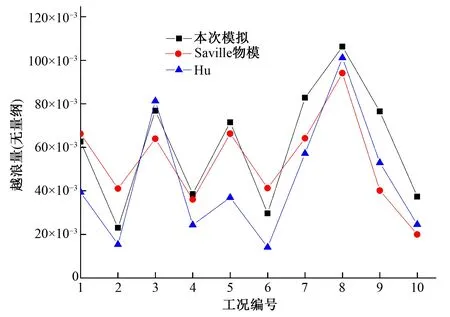
图5 规则波越浪量模拟结果对比Fig.5 Comparison of regular wave overtopping discharges
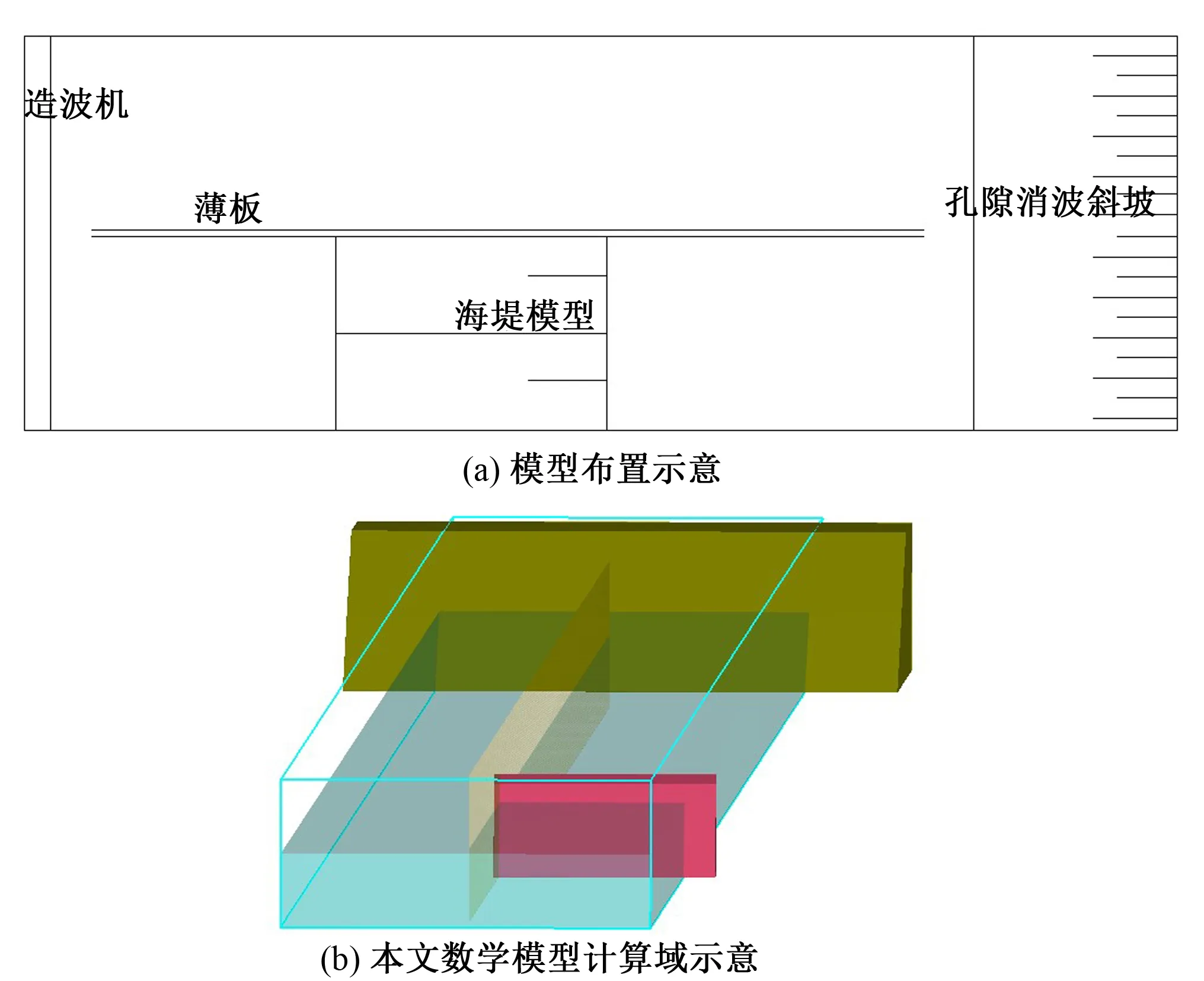
图6 不规则波越浪模型布置示意Fig.6 Sketch of the model layout for the irregular wave overtopping
模型采用的复式断面海堤分为下坡、上坡以及连接上下坡的平台3个部分,如图7(a)所示。其中,md为下坡坡度,mu为上坡坡度,b为平台宽度,dw为平台上水深(平台高于静水位取正值,反之取负值),Hc为堤顶相对于静水面的高度。
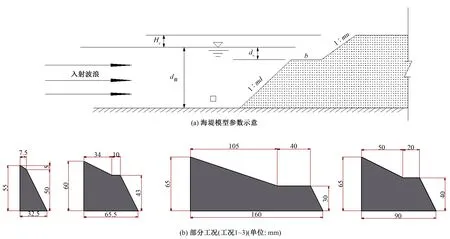
图7 复式海堤模型示意Fig.7 Sketch of the composite section sea-dike
本文选取的断面参数共8组,如表2所示。其中,部分海堤断面(工况1~3)示意图如图7(b)所示。本文采用的入射波有效波高HS=0.1 m,谱峰周期Tm=1.25 s。
3.2 模拟结果验证
数值模拟得到的无量纲越浪量与物模试验成果的对比如表2、图8所示,其中q为单宽越浪量。由结果对比可以看出,数模结果与物模成果基本吻合,但数值总体偏小,这可能是由于不规则波模拟更易发生数值耗散造成的。
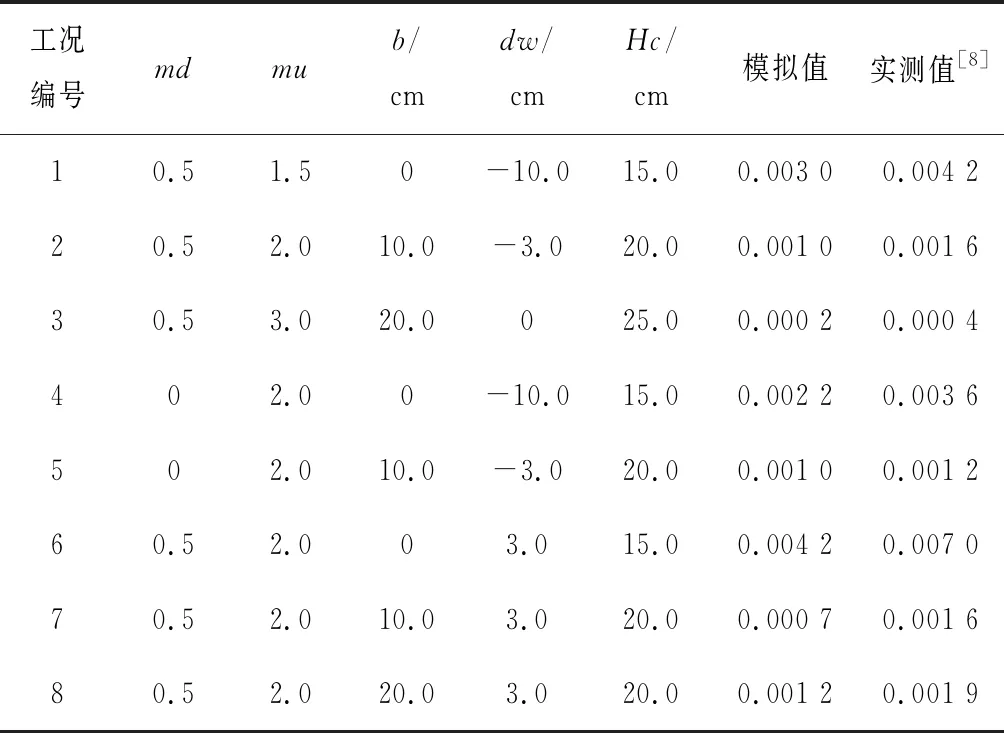
表2 复式断面参数及模拟结果对比Tab.2 Comparison of sea-dike parameters and simulation results for overtopping discharge
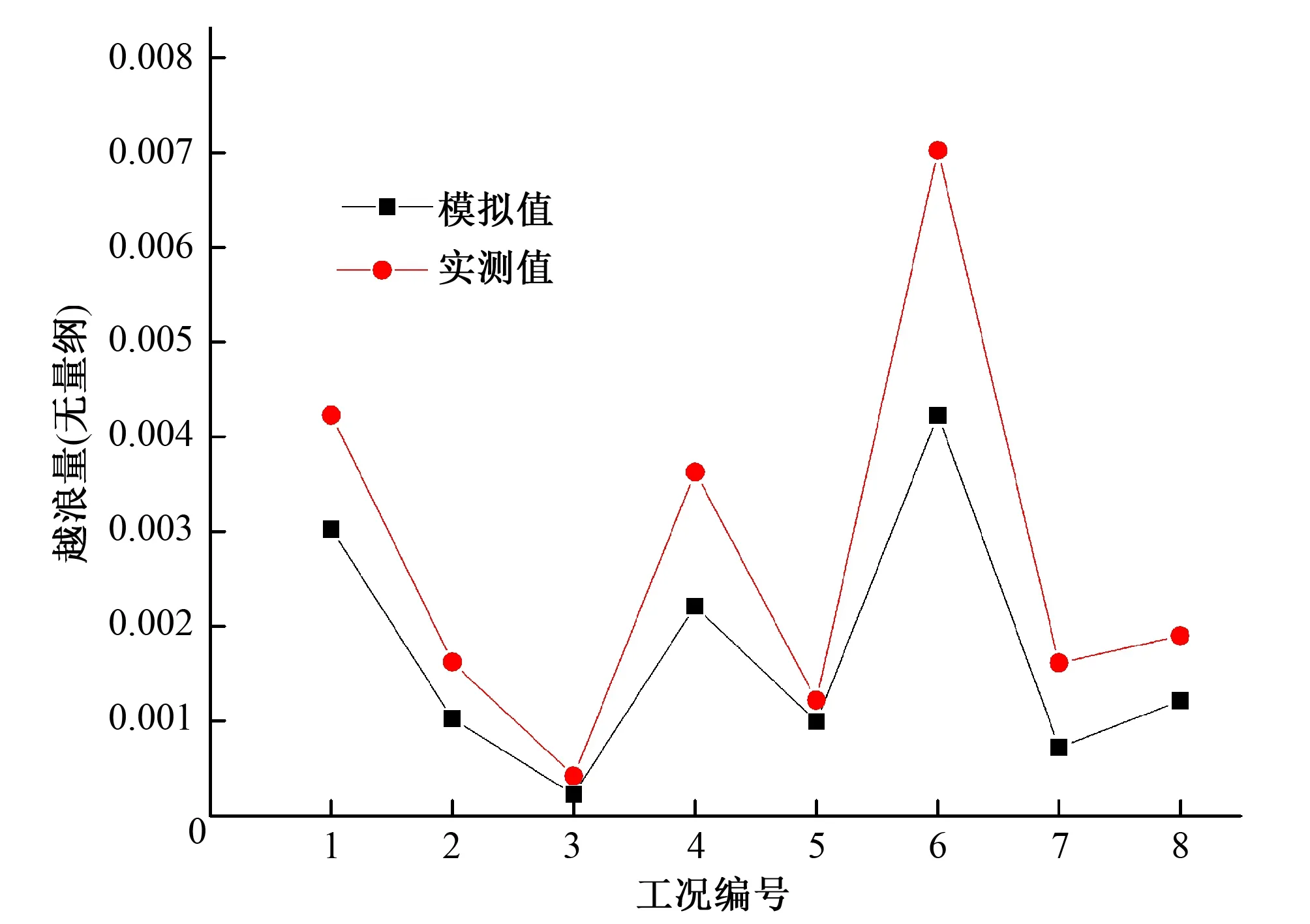
图8 不规则波越浪量模拟值与实测值对比Fig.8 Comparison of irregular wave overtopping discharges
3.3 越浪过程分析
根据模拟结果,分别以不带平台和带平台的典型工况为例,分析越浪过程。图9和图10分别是工况6(不带平台)以及工况8(带平台)典型越浪过程的流场分布图。
由图9可知,模拟时刻t=13.6 s时,上一个波浪刚退去,水体流向为远离海堤方向。自此开始越浪过程大致分为3个阶段。其中,第一阶段为上坡阶段,即13.8~14 s时较大波浪开始接近,14.2 s时表层水体流速约为1 m/s,14.4 s时水体进入海堤上坡爬高阶段,至此堤前水体整体流向为向堤方向。
第二阶段为爬高和越浪阶段。14.6 s时堤脚附近下层水体开始出现回流,14.7 s时回流范围扩大,在爬高过程中堤前水流逐渐分为两部分:下层水体被下坡反射回流,上层水流沿上坡继续向上运动。14.8 s时,两部分水流分界点到达折坡点附近。14.9 s时,分界点继续上移,上坡水流开始整体分离为两部分:一部分在惯性作用下继续爬高并在堤顶发生越浪,另一部分开始整体回流。
第三阶段为退浪阶段。15.1 s时,无法发生越浪的残余水流在重力作用下回落,并逐渐加速。15.3~15.5 s,回落水流在堤前形成空腔。与此同时,下一个波浪开始接近海堤。此时上述第一阶段和第三阶段同时发生。15.6 s后续波浪带来的水流将空腔淹没,并在堤脚附近形成流动状态较为复杂的涡旋区。15.8 s再次开始重复上坡爬高过程,即上述第二阶段。
由此可以看出,由于波浪的不规则性,越浪过程的各个阶段并不一定存在严格的时间界限,而是可能相互重叠。同时,与14.4 s时开始的上坡爬高不同的是,15.8 s时,由于前一时刻的大波浪发生了越浪,回落水流导致堤脚处的流动状态更为复杂,由此也可以看出波浪对堤脚处的淘刷主要发生在大波浪作用时。
带平台海堤越浪过程和无平台海堤基本一致,仍大致分为3个阶段。但在第三阶段,由于平台的存在,延长了水流回落的距离和时间,回落过程更易遭遇下一个波浪。以工况8为例,如图10所示,回落水流经过平台时流向基本水平,此时与来波相撞,在堤前形成水体壅高,然后再向两个相反方向回落、流动,水流流速比相撞前明显减小,波能迅速衰减海堤越浪量相应减小。这是带平台海堤的消浪机制之一。
4 结 论
(1)基于RANS方程和VOF方法,利用边界造波技术和多孔介质结合辐射边界的消波技术,生成Stokes五阶波和JONSWAP谱波,数值解与理论解吻合较好,说明模拟的准确性和计算效率较高。
(2)针对两种典型的复式海堤断面型式,即两段式折坡海堤以及下坡陡、上坡缓、中间为平台的三段式海堤,开展的规则波和不规则波越浪模拟结果表明,模拟值与物理模型试验值规律性一致,吻合较好,表明模型能较准确地模拟海堤越浪,为下一步开展参数化研究并应用于工程实际奠定了基础。
(3)针对不规则波越浪模拟工况,采用沿波浪传播方向放置隔板的方式,将水槽一分为二,在减少波浪二次反射的同时保持了水槽内水位恒定,收到良好效果,可为同类模拟提供参考。

图9 无平台海堤不规则波越浪过程(工况6)Fig.9 Irregular wave overtopping process over sea-dike without platform (Case 6)
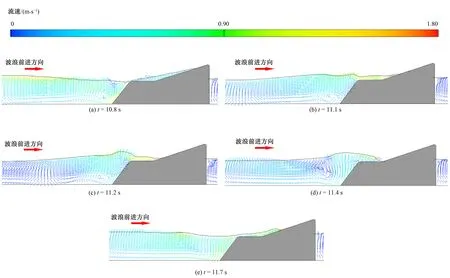
图10 带平台海堤不规则波越浪过程(工况8)Fig.10 Irregular wave overtopping process over sea-dike with platform (Case 8)
(4)采用流场分析手段,分析波浪与海堤相互作用的3个阶段,可以发现海堤除受到波浪正面冲击力外,迎水面特别是堤脚附近还会受到退浪和上浪过程形成漩涡的淘刷;三段式海堤所带平台可延长退浪水流的回流距离和时间,部分抵消上浪水流动能,是带平台海堤的消浪机制之一。
□

