一种可考虑形状效应的浅埋板锚极限抗拔力计算方法

郭京平

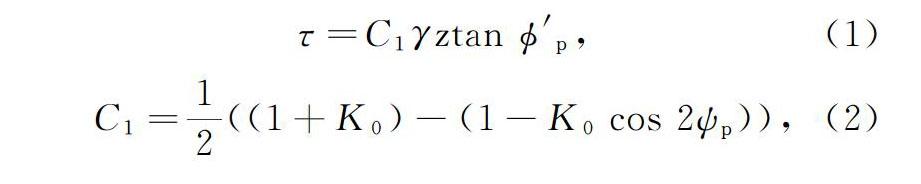
摘要：现有的板锚极限抗拔力计算方法只考虑了常规形状锚板的情况，不适用于特殊形状的锚板。为了更好地指导工程实践，在总结已有研究的基础上，研究了圆形、方形、正三角形和风筝形锚板，假定锚板的破坏面从锚板的侧面以膨胀角向上延伸，形成与锚板自身具有相同横截面形状的棱台，结合数学和力学理论分析，提出了一种可以考虑形状效应的浅埋板锚极限抗拔承载力计算方法，并将简化方法计算所得承载力和公开试验结果进行对比。结果表明，简化计算方法适用于埋深与板宽之比小于5的浅埋情况，且具有较高的精度，可以在初步工程设计中加以应用。研究结果为多种形态的浅埋锚板极限抗拔力计算提供了新的方法，可为类似工程项目的设计提供参考，具有一定的工程借鉴价值。

关键词：岩土力学;形状效应;浅埋板锚;极限抗拔承载力;简化计算

中图分类号：TU443文献标识码：A

doi： 10.7535/hbgykj.2020yx03004

Abstract：

The existing calculation method of the ultimate pullout force of plate anchors only considers the regular shapes， Which is not applicable to the special shapes. In order to better guide the engineering practice， the circular， square， equilateral triangle and kiteshaped anchor plates were studied based on the previous research， assuming that the failure surface extended upward from the side of the anchor plate at a specific expansion angle， which resulted in the same shape as the crosssection of the anchor plate. Combining with the particular mathematical and mechanical theoretical analysis，

a calculation method taking the shape effects into account was proposed to analyze the ultimate pullout force

of shallowburied plate anchors， from which the results were compared with the publicly available experimental data. The results show that this method has high accuracy when the ratio of the buried depth to the board width is less than 5， and can be applied in preliminary engineering design. The research results provide a

new way for the calculation of the ultimate pullout force of various shapes of shallow buried anchor plates，

which can also offer areference for the design of similar projects.

Keywords：

geotechnical mechanics; shape effect; shallow plate anchor; ultimate uplift bearing capacity; simplified calculation

海上发电平台由固定在结构上的锚定系统固定，而锚定系统与各种锚相连接，如桩锚、板锚、吸力沉箱、拖曳锚、吸力嵌入式板锚和动态穿透锚等[1]。桩锚主要通过侧阻提供反力，而板锚主要通过板支撑面提供阻力，侧阻力不如支撑面阻力有效，而且容易在循环荷载作用下出现承载力和刚度退化现象[2]，因此，与桩锚相比，板锚的应用更加广泛。

用于近海能源部门的新型动力穿透板锚概念，如飞翼锚[34]已经在研发中，这些板锚均可以抵抗较大的横向荷载。而现有的板锚极限承载力计算方法多针对常规形状的锚板，如圆形锚板[58]和矩形锚板[911]，对一些特殊形状的锚板是不适用的。虽然三维非线性连续体分析方法[1215]可以用来分析特殊形状的板锚的极限承载力，但在基础设计工作中，简化设计方法仍然是工程设计人员所需要的。

1极限抗拔力计算

理论分析方法可以用来评估板锚的极限承载力。现有的用于预测砂土中板锚抗拔承载力的方程通常是基于峰值摩擦角的[5，1617]。這些方程有的是基于关联极限平衡原理建立的，该原理的核心假设是峰值膨胀角等于峰值摩擦角。有的研究基于假设“由摩擦角能够唯一确定膨胀角”。新的研究[1819]已经表明，关联流的假设不能反映土体的排水剪强度，并且高估了排水条件下的地基承载力。因此，

对破坏面可能向泥线延伸的浅锚而言，膨胀角应直接包含在抗拔承载力分析中。

为解释浅埋板锚上拔过程中出现的土体体积扩大问题，CHEUK等[20]提出了平面应变条件下的非关联极限平衡抗拔承载力模型。如图1所示，该模型假定上拔破坏面以等于土体膨胀角的角度出现。CHEUK等[21]和LIU[22]等通过实验验证了这种非关联流假设。拔出阻力等于提升土楔的重力加上沿2个倾斜破坏面的剪切阻力。土楔的重力取为二维梯形体积部分土体对应的重力，假定破坏面上只考虑摩擦耗能，则剪切阻力可以表示为

2简化公式计算结果与已有试验结果的对比

尽管笔者提出了簡化的不同形状锚板的抗拔极限承载力的计算公式，但这些公式均建立在一定的假设基础上，计算精度有待检验。为明确板锚的抗拔机理，国内外学者进行了大量的板锚抗拔试验，考虑到GIAMPA等[25]的试验结果原始数据比较充分，而且对各种形状锚板均进行了试验，因此笔者

将简化公式的计算结果与已有试验结果进行对比。

试验中所采用的土体物理力学参数和锚板数据如表1所示，将试验得出的极限抗拔承载力Qu除以γHA即可以得出最后一列的极限承载力系数。

试验结果和简化公式计算结果的对比如表2所示。除圆形锚板确定符合轴对称条件外，其他形状的锚板都不严格符合轴对称条件，因此计算其他形状锚板时，同时考虑了轴对称条件和平面应变条件，2种情况对应的C1取值不同，平面应变条件下C1表达式如式（2）所示，轴对称条件下C1表达式如式（10）所示。相对误差的计算为计算值减去试验值取绝对值后除以试验值。

从表2中的圆形锚板情况可以看出，对圆形锚板简化公式预测承载力平均误差在15%以内，变异系数为0.18，这与GIAMPA等[24]的研究结果是一致的。对方形、正三角形和风筝形锚板的情况，平面应变条件下简化公式得出的承载力比轴对称条件下得出的承载力更符合试验结果，这表明在非轴对称情况下，破坏面上法向应力作用更符合平面应变情况。建议在使用简化公式时，除轴对称情况外，一律采用平面应变模式。

如表2所示，对正三角形锚板，考虑平面应变情况，试验编号为20所对应的误差为63%，此时对应的埋

深H与板宽B之比（如表1所示）为0.635/0127=5，对其他H/B<5的正三角形锚板误差均小于25%，这直接表明对于正三角形锚板，简化公式只适用于H/B<5的浅埋情况。对方形和风筝形锚板做类似的分析，同样能得出简化公式只适用于H/B<5的浅埋情况的结论。

分析表1和表2的数据，可以看出，对方形锚板、正三角形锚板和风筝形锚板，当H/B>5时简化公式计算的误差会加大，对H/B<5时的浅埋情况，3种锚板计算误差均值分别为14%，14%和16%。因此，本文中的简化公式适用于H/B<5的浅埋情况。

3结语

在结合前人工作经验的基础上，结合一定的理论分析，提出了可考虑锚板形状的简化的板锚极限抗拔力计算方法，并将该计算方法所得结果与已公开的试验结果进行对比，主要得出如下结论。

1）破坏面从锚板的侧面以膨胀角向上延伸的假定是合理的。将理论分析方法用于板锚抗拔极限承载力分析是可行的。

2）简化公式使用时，除轴对称情况外，一律采用平面应变模式，并且只适用于埋深与板宽之比小于5的浅埋情况。

3）研究结果弥补了目前仅有常规形状锚板计算的缺陷，为多种形态的浅埋锚板极限抗拔力计算提供了理论依据，可为类似工程项目提供可靠的设计参考依据，值得工程借鉴应用。

本文的研究范围仅局限于浅埋锚板的情况。虽然工程中常见的锚板都是浅埋锚板，但是对于深埋锚板所对应的承载力研究也是工程所需要的。另外，本文采用理论分析方法进行抗拔力计算研究，建议采用有限元分析方法或者离散元方法研究形状效应对抗拔力的影响，以更好地指导工程实践。

参考文献/References：

[1]RANDOLPH M，GOURVENEC S. Offshore Geotechnical Engineering[M].England：[s.n.]，2011.

[2]JARDINE R， PUECH A， ANDERSEN K H. Keynote address： Cyclic loading of offshore piles： Potential effects and practical design[J]. Journal of Environmental Science and HealthPart A Environmental Science and Engineering， 2012， 11（10）： 591601.

[3]BRADSHAW A S， GIAMPA J R， GERKUS H， et al. Scaling considerations for 1g model horizontal plate anchor tests in sand[J]. Geotech Testing Journal， 2016， 39 （6） ： 19.

[4]CHOW S， O LOUGHLIN C D， GAUDIN C， et al.  An experimental study of the embedment of a dynamically installed anchor in sand[C]//Offshore Site Investigation Geotechnics 8th International Conference Proceeding. London：[s.n.]，2017：10191025.

[5]MERIFIELD R S， LYAMIN A V， SLOAN S W. Threedimensional lowerbound solutions for the  stability of plate anchors in sand[J]. Géotechnique， 2006， 56（2）： 123132.

[16]GHALY A， HANNA A. Ultimate pullout resistance of single vertical anchors[J]. Canadian Geotechnical Journal， 1994， 31（5）： 661672.

[17]ILAMPARUTHI K， DICKIN E A， MUTHUKRISNAIAH K. Experimental investigation of the uplift behavior of circular plate anchors embedded in sand[J]. Canadian Geotechnical Journal， 2002， 39（3）： 648664.

[18]LOUKIDIS D， CHAKRABORTY T， SALGADO R. Bearing capacity of strip footings on purely frictional soil under eccentric and inclined loads[J]. Canadian Geotechnical Journal， 2008， 45（6）： 768787.

[19]KRABBENHOFT K， KARIM M R， LYAMIN A V， et al. Associated computational plasticity schemes for Nonassociated frictional materials[J]. Computational Plasticity Schemes for Nonassociated Frictional Materials， 2012， 90（9）： 10891117.

[20]CHEUK C Y， BOLTON M D， WHITE D J. The uplift resistance of pipes and plate anchors buried in sand[J]. Géotechnique， 2008， 58（10）： 771779.

[21]CHEUK C Y， WHITE D J， BOLTON M D. Uplift mechanisms of pipes buried in sand[J]. Journal of Geotechnical and Geoenvironmental， 2008， 154 （2）： 154163.

[22]LIU Jinyuan， LIU Mingliang， ZHU Zhende. Sand deformation around an uplift plate anchor[J]. Journal of Geotechnical and Geoenvironmental， 2012（102）： 728737.

[23]GIAMPA J R， BRADSHAW A S， SCHNEIDER J. Influence of dilation angle on drained shallow circular anchor uplift capacity[J]. International Journal of Geomechanics， 2016， 17（2）：04016056.

[24]GIAMPA J R， BRADSHAW A S. A simple method for assessing the peak friction angle of sand at very low confining pressures[J]. Geotechnical Testing Journal， 2018，38（8）：16061618.

[25]GIAMPA J R， BRADSHAW A S， GERKUS H， et al. The effect of shape on the pullout capacity of shallow plate anchors in sand[J]. Géotechnique， 2018， 69（4）： 355363.