具有不变直线的非Hamilton系统的极限环分支
张二丽,邢玉清
(1. 郑州财经学院 信息工程学院,河南 郑州 450044;2. 河南农业大学 理学院,河南 郑州 450002)
实平面微分系统定性理论的一个主要问题是确定它们极限环的个数, 其中通过扰动具有中心的微分系统产生极限环是一种经典方式。一般来说, 研究从一个微分系统的中心周期环域分支出极限环个数有4种方法: Poincaré回归映射法[1]、 Poincaré-Pontrjagin-Melnikov法或Abelian积分法、逆积分因子法[2]和平均法[3],其中前2种方法在平面上是等价的[4]。在一定条件下平均法与Abelian积分法也是等价的[5]。平均法给出了非自治周期微分系统的解和其平均微分系统的解之间的定量关系, 平均微分系统是一个自治微分系统, 研究起来较简单, 而且一阶平均微分系统的双曲平衡点的个数给出相应非自治周期微分系统极限环的最大个数的一个下界。当一阶平均函数等于零, 极限环的个数依赖于二阶平均函数, 依次类推[6]。更多相关的研究可参看文献[7-11]。
文献[2]研究了如下形式的扰动可积微分系统
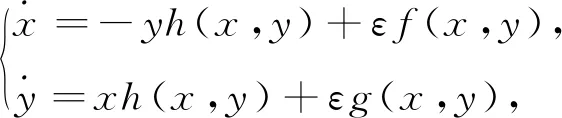
(1)
式中h(x,y)=0是R2上使得h(x,y)≠0的圆锥曲线。当f(x,y)和g(x,y)都是3次多项式时, 他们应用一阶平均法得到了系统(1)的极限环的最大个数。当f(x,y)和g(x,y)是任意n次实多项式时, 应用一阶平均法:文献[12]研究了h(x,y)=x+1;文献[13]研究了h(x,y)=(x+a)(y+b), 其中ab≠0; 文献[14]研究了h(x,y)=(x+a)(y+b)(x+c), 其中abc≠0; 文献[15]研究了h(x,y)=y2+ax2+bx+c, 其中c≠0。应用二阶平均法, 文献[16]研究了h(x,y)=(a1x+a0)(b1y+b0), 其中aibi≠0(i=1,2)。
本文研究如下扰动可积微分系统
(2)
式中0<|ε|≪1,
(3)
易知, 当ε=0时, 系统(3)有首次积分H(x,y)=x2+y2, 原点是该系统的一个中心, 且该系统有一对不变直线x=±1。本文主要结果如下:
定理1当0<|ε|≪1时, 系统(2)恰好存在n个极限环。
1 平均法
本章介绍微分方程的平均法, 详见文献[17]。
定理2考虑如下微分方程的初值问题
(4)
其中F0(x,t)和G0(x,t,ε)是关于t的T-周期函数,x,x0∈U,T是不依赖于ε的常数,U是R中的开区间。定义平均函数
再考虑平均方程的初值问题
(5)
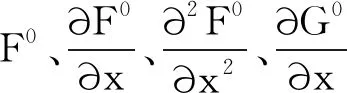
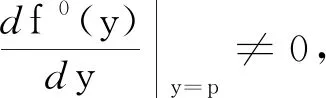

注1 由定理2可知, 如果方程(4)满足定理中的条件, 则平均函数f 0(y)的每个简单零点对应方程(4)的一个极限环,所以计算出平均函数f 0(y)至关重要。
2 平均函数
本章将计算平均函数的具体表达式。令
x=rcosθ,y=rsinθ,r∈(0,1),
则式(2)可化为
所以
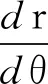
(6)
其中
容易验证, 方程(6)满足定理2中的条件。根据定理2, 与方程(6)相对应的平均函数为
(7)
下面化简平均函数f0(r)。由式(3)可得
(8)
其中λi,j=ai-1,j+bi,j-1, 这里假设λ0,0=a-1,j=bi,-1=0。因为ai,j和bi,j是可以任意选取的, 所以λi,j也是可以任意选取的。为了方便, 定义
(9)
易知, 当k是奇数时,M(k)=0; 当k是偶数时,M(k)≠0,且M(0)=1。
引理1下列关系式成立:
①rI0,j(r)=M(j-1)-I0,j-1(r);
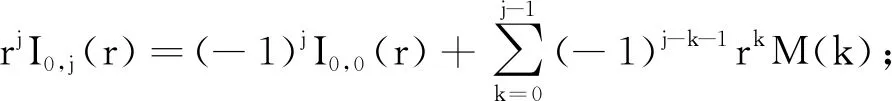
③rJi,j+1(r)=Ii,j(r)-Ji,j(r);
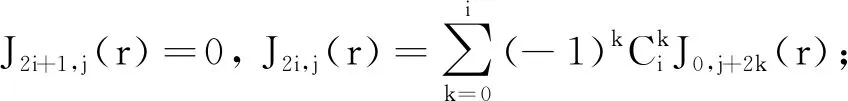
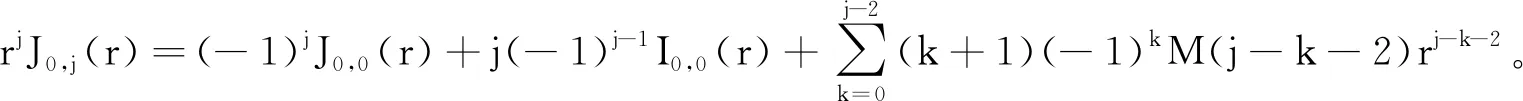
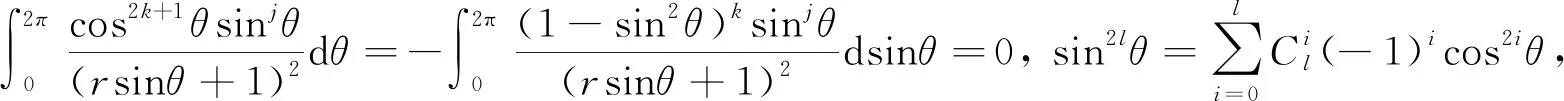
由①知, 当j=1,2时, ⑤成立。假设当j=l时, ⑤成立,则当j=l+1时, 由①和②可得
rl+1J0,l+1(r)=rl[I0,l(r)-J0,l(r)]=
所以当j=l+1时⑤成立。证毕。
注2 令F(r)=rf 0(r), 则F(r)和f 0(r)在区间(0,1)上的零点个数相同。所以下面求F(r)在区间(0,1)上的零点个数。
对整数n,用[n]表示不超过n的最大整数。
引理2函数F(r)可以表示为
(10)
式中:
证明由式(9)、(10)和引理1可得
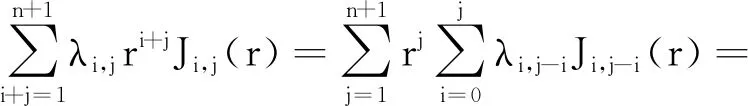
(11)
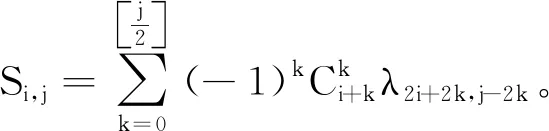
可得
I0,0(r)=(1-r2)J0,0(r)。
(12)
把式(12)代入式(11), 并注意到当k是奇数时M(k)=0, 即可得式(10)成立。证毕。
注3 由式(10)可知, β0=-α0。


证明如果n是奇数, 由式(10)可得

如果n是偶数, 可类似地证明。证毕。
3 主要结果的证明
为了证明本文定理1, 还需要下面引理。
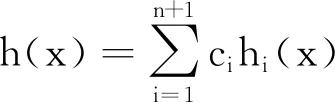
引理5对于系统(2),如下结论成立:

(13)
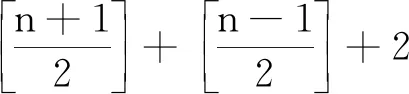
(14)

(15)
类似地可以证明结论②成立。证毕。
下面证明定理1。
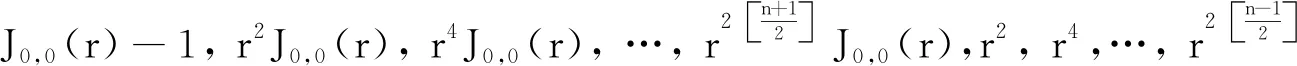
由式(10)可知, 当n是奇数时,
(16)
令ξ=r2, 则式(16)变为
(17)
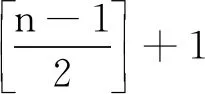


即可得定理1成立。证毕。

