基于FPGA的控制算法定点化设计

衡 园，吴建成，杨志军

（广东工业大学 广东省微纳加工技术与装备重点实验室，广东 广州 510006）

随着复杂控制系统开发的需求日益增大，现场可编程逻辑门阵列(FPGA，field programmable gate array)与基于模型设计的联系也越来越紧密[1]。在simulink仿真过程中由于浮点运算的精度比较高，所以模型大多都采用浮点数格式。当要将模型下载到硬件平台中时，则需将算法模型的数据类型转化成定点数格式。随着FPGA的性能发展，现有的FPGA器件支持浮点运算，但浮点算法在FPGA硬件上实现时会占用大量的FPGA芯片内部资源[2]，因此使用FPGA来实现复杂控制算法时，首先需要将算法的数据类型转化为定点数格式。数据类型由浮点转化到定点数过程中不可避免地会产生精度损失，因此需要对算法模型计算精度进行评估，选择合适的数据位宽，使得FPGA在消耗尽量少的内部资源时，同时满足控制算法精度要求[3]。借助simulink中定点工具(Fixed-Point Tool)箱对算法模型数据动态范围进行分析，并会给出其建议的数据定点位宽，然后人为地在其建议的数据位宽基础上适当增减位宽，使算法内各部分既能满足精度要求，又能使数据的位宽控制在合适的范围内，以实现在将算法部署到FPGA上时不会造成其内部资源的浪费[4]。

1 运动控制算法模型介绍

如图1所示，运动控制算法模型主要由4部分组成，即运动规划曲线、位置反馈数据输入、控制算法、结果输出。该算法模型已在实际平台进行验证，能较好地控制平台的运动。该控制算法有两个输入端，其实际物理意义是位置，因算法内部进行计算时采用的是标准单位米(m)，而平台实际运动的距离一般在几十厘米左右，所以可知带入算法模型的数值为小数，在算法内部进行一系列积分、微分、加减乘除运算后，小数位长将会非常大[5]。在simulink仿真过程中为保证数据精度,采用的是双精度浮点型(double型)[6]。当要在FPGA中实现浮点运算时，考虑到会大量浪费FPGA内部资源等因素，因而需要对算法中的数据类型进行定点化处理[7]。

与浮点数相比，定点数的小数点在数据的位置是固定的，没有浮点数尾数对齐和归一化问题，所以在硬件实现时，其性能更高。但是，由于定点数表示数据范围较小，在实际运算过程容易出现溢出和病态方程等问题[8]。

2 运动控制算法模型的定点化流程

2.1 对控制算法模型重新搭建

为了将图1模型中的控制算法部分集成到FPGA，需要在使用simulink中的HDL coder库将控制算法转换成HDL语言之前进行前期准备工作[9]。(1) 需要检查模块兼容性。HDL code库作为simulink模型库中的子库，其中的功能模块并非齐全[10]。因此在使用HDL code库重新搭建控制算法时，可能存在HDL code库中没有的模块，这时就需要对原算法模型做相应的转换。(2) 找出可能无法定点化的函数模型。例如，在进行三角函数、除法以及求根等运算时，需要将其转换成能够定点化的算法，如查表法等[11]。

2.2 Fixed-Point Tool收集数据动态范围与精度

在对控制算法模型进行重新搭建后，在sumulink中将图1中运动规划曲线、位置反馈数据输入部分的输入信号连接重建的算法模型，做一次仿真，此时simulink会根据输入数据的范围得到算法模型各部分数据范围。Fixed-Point Tool首先根据仿真结果收集数据的范围，然后根据数据的范围给出其建议的数据位宽[12]。如图2所示，给出内部数据信号直方图信息。

图2中左上部分给出了信号仿真过程中出现的最大值和最小值，以及定点化数据位宽等信息。左下角给出信号数据对应的直方图，右边部分给出了直方图中指定信号的详细信息，如建议数据类型、数据建议范围以及数据上溢、下溢的可视化图形[13]。

2.3 使用建议位宽对数据进行定点化结果分析

在Fixed-Point Tool工具中可以根据其操作流程在算法模型各部分使用建议的数据位宽，然后做一次仿真，工具会自动比较定点化模型与未定点化之前的double型模型的输出结果，如图3所示。

由图3可知，控制算法在做定点化前后其输出结果的曲线基本吻合。图4给出了比较结果的详情，可以看到，控制算法在整个仿真的时间数据内将误差范围控制在±0.008，只有较短的时间超出范围。由于本算法模型是应用在控制领域，对数据的精度要求较高，如果数据精度达不到要求，那么最终的控制效果将会非常差，甚至可能导致算法失效[14]。

3 根据建议数据位宽适当修改位宽

控制算法在FPGA上实现，其关键问题在于保证算法精度的情况下将浮点数转换成能在FPGA运行的定点数。在使用Fixed-Point Tool定点化时首先需要设置转化成定点数的位宽，然后工具根据给定的数据位宽分配算法中数据的整数、小数各部分所占的位宽[15]。由于控制算法内部是复杂的数学运算，输入和输出的数据范围会出现差别很大的情况。例如，输入是小数，输出可能是比较大的整数的情况。此时如果按照Fixed-Point Tool在转换成定点数前将算法各部分设置成统一长度的位宽显然是不合适的。如果将位宽设置得较长，可以保证内部数据的精度，但考虑到最终将算法部署到FPGA中，采用较长的位宽将耗费大量FPGA内部资源，并且增加算法在FPGA中计算的延时；若采用较短的位宽，那么在经过算法计算后数据的精度可能达不到要求[16]。因此，需要根据算法内部各部分数据范围动态地设置其位宽长度，这样既能保证数据位宽在合适的范围内，又能保数据定点化后的精度。

图 2 内部数据信号分析Fig.2 Internal data signal analysis

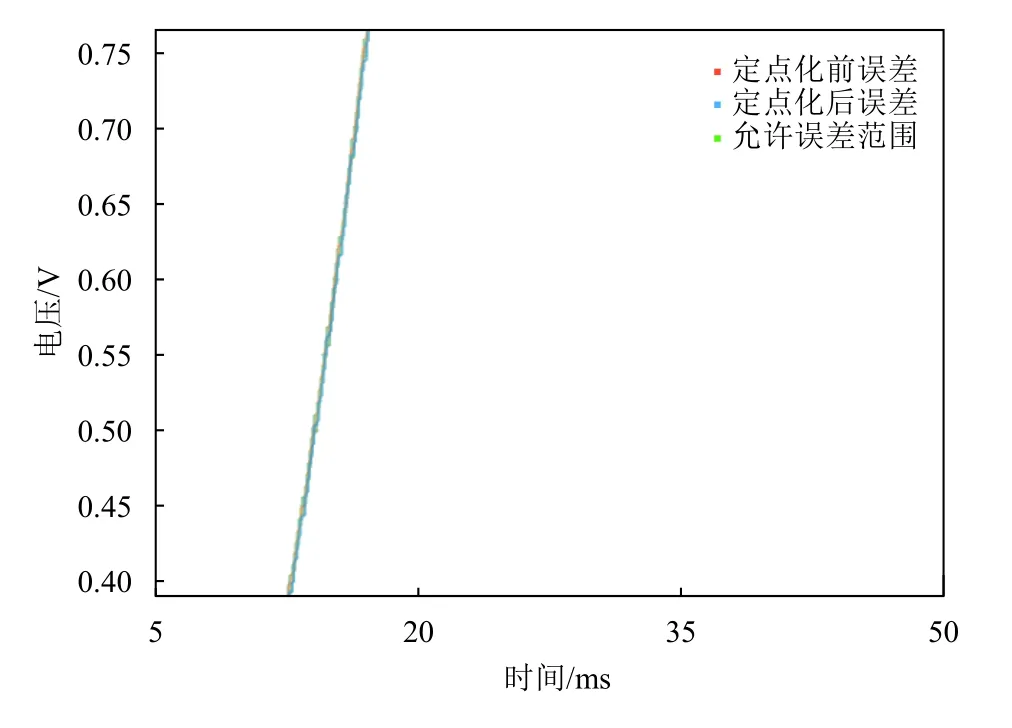
图 3 定点前后输出结果曲线重合度Fig.3 Output coincidence curve before and after fixed point

图 4 建议数据位宽时的误差Fig.4 Error when recommending data width

如图2所示，在Fixed-Point Tool中设置转化的定点位宽为16位，可以看到其给出的建议位宽都是16位格式。fixdt(X，Y，Z)中X表示符号位(0表示无符号，1表示有符号)，Y表示数据位宽，如设置数据位宽为16位，Z表示小数位的长度。图2中可以看到sum:Output数据给出的数据位宽格式fixdt(1，16，17),说明如果要保证数据定点化达到设定精度需要17位的小数，然而数据位宽只有16位。通过图2左下角的直方图分析，“Potential Underflows”一项的数据位21，说明如果采用16位的数据位宽做定点化时将会出现数据溢出的情况。此时需要适当增加sum:Output的数据位宽，解决数据溢出问题，使数据都在定点数的表示范围内。

根据上述分析，对算法内部其他部分做相同的调整，使数据都在对应数据位宽的表示范围内。此时，再次对定点化前后的数据做对比，结果如图5所示。从图5中可以看到经过人为适当调整数据的位宽，定点前后数据误差控制在-3.5×10-6以下，能够满足控制算法所需的精度要求。

图 5 自定义数据位宽时的误差Fig.5 Error in custom data bit width

4 结束语

针对控制算法在FPGA上实现过程中数据类型转换问题，在使用simulink中Fixed-Point Tool对数据范围进行提取和给定参考定点数据位宽基础上，人为地对算法内部各部分的数据位宽做适当的调整，从而使算法既能保证较高的精度，又能解决Fixed-Point Tool采用统一较长位宽时造成FPGA内部资源的不必要消耗和延时问题，实现了复杂控制算法部署到FPGA上实现高速、高精度运算。