一种基于PCB工艺的平面绝对式角位移传感器研究

景 欢，汤其富，王阳阳,2，刘 洋

(1.重庆理工大学，机械检测技术与装备教育部工程研究中心，重庆 400054；2.重庆大学，机械传动国家重点实验室，重庆 400044)

0 引言

传感器是一种测量信息的工具，在生产制造和工业现场等场合起着信息源作用[1]。基于电磁感应的位移传感器在恶劣工业条件下具有明显优势[2-7]。以旋转变压器为例，因其具有抗干扰能力强、适合较恶劣工况等优势广泛应用于各种工业场合，但受限于原理结构等，使其测量精度和分辨力较低[8-10]。要实现高精度测量无法兼顾尺寸，因此较庞大的外形结构制约了其发展。相较而言盘式的感应同步器和磁场式时栅传感器通过机械结构的优化实现了体积上的缩减[11-15]，但其结构限制了在绝对式测量方法的应用，仍然存在开机需要找零、狭窄形机械空间无法安装等问题。基于此，本文提出了一种基于PCB工艺的电磁感应式角位移传感器结构，设计并利用“差极式”测量模式实现绝对式角位移测量[16]。

1 单传感通道传感器的结构和工作原理

1.1 单传感通道传感器的结构

根据文献[15]介绍的主动约束磁场型角位移传感器具有单传感通道的结构特征，如图1所示，该类型的传感器虽然精度较高，但是无法实现绝对式测量。

图1 单传感通道传感器结构示意图

1.2 单传感通道传感器工作原理

根据磁场式时栅传感器的基本工作原理，实现位移测量需要构建传感器的时空双正交[15]。时间正交表现为激励线圈直接通入两相正交激励信号实现；空间正交表现为两相激励线圈相差1/4重复结构周期。激励线圈中分别通入式(1)和式(2)所示的两相时间正交的正/余弦信号：

e1=Amsin(ωt)

(1)

e2=Amcos(ωt)

(2)

式中：Am为激励信号的幅值；ω为激励信号的角速度。

由于激励线圈在空间上呈正交关系布置，因而当激励线圈中通入正交信号后，随着转子的旋转，感应线圈中的磁通量Φ将随之而改变，Φ的变化与时间t和转子的角位移θ呈函数关系，该函数关系如式(3)所示：

(3)

式中k为与传感器结构相关的常数。

f1(θ)和f2(θ)如式(4)所示：

(4)

(5)

(6)

式中Np为传感器结构重复周期数。

为了计算出传感器转子的角位移量，需要对感应线圈输出的感应信号进行处理。输出的感应信号比较微弱并带有大量的噪声，通过采用文献[15]中所述的信号处理和角位移量解析方法，可以得到如式(7)所示的被测角位移量。

(7)

式中：n为转子转过的周期数；Δt为感应信号转化为方波后其上升沿与参考方波上升沿之间的时间差。

2 双传感通道传感器的结构和工作原理

2.1 双传感通道传感器的结构

为了实现绝对式测量，本文所采用的传感器具有2个传感通道，二者具有独立的激励线圈，但共用感应线圈。2个传感通道的重复结构周期数相差为1，设为N和(N+1)。本文将传感单元的激励环形正弦线圈和感应线圈印制在电路板上，同时转子结构采用铜箔阵列。该传感器制造方法不仅可以使传感器厚度小，而且线圈的布置可以灵活和精确控制，从而达到传感器工作所需的时变磁场精确约束。传感器的结构如图2所示，图2(d)和(e)中，A、B、G和H焊盘为N周期激励线圈Ca1、Ca2、Ca3和Ca4的输入接口，布置在电路板的内圈；C、D、E和F焊盘为(N+1)周期激励线圈Cb1、Cb2、Cb3和Cb4的输入接口，布置在电路板的外圈；I和J焊盘为感应线圈Ci的输出接口。

图2 双传感通道传感器结构示意图

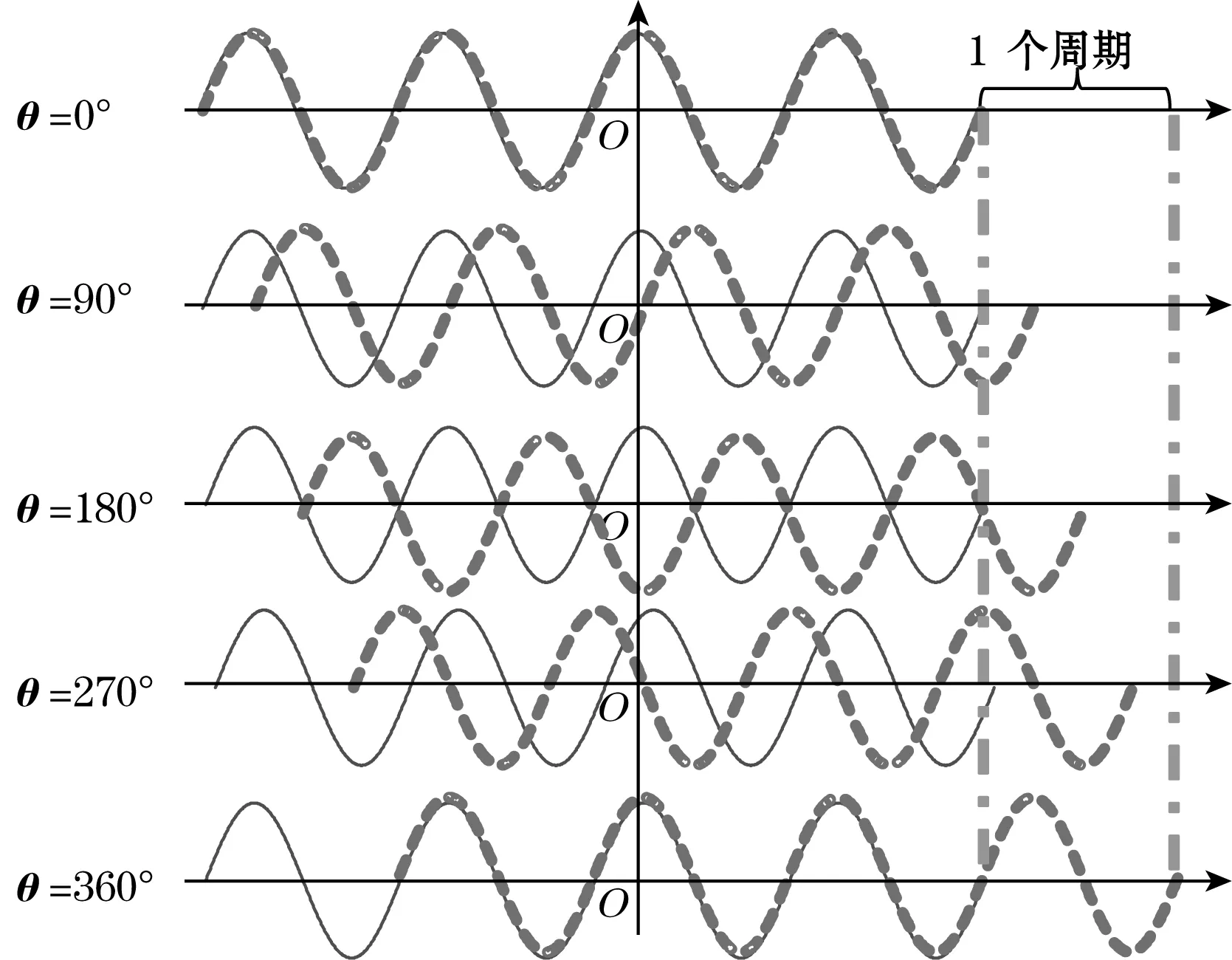
图3 N+(N+1)周期传感通道输出信号变化过程示意图

2.2 双传感通道传感器的工作原理

前文提及利用N+(N+1)重复结构周期数的双传感通道，组合实现绝对式测量，其原理可以通过图3所示的信号变化示意图进行描述。在转子转动过程中，2个传感通道的感应线圈输出两种不同的信号。转子转动1周，在N周期激励线圈的磁场作用下，感应信号的相位变化N个电信号周期，而(N+1)周期激励线圈的磁场作用下，感应信号的相位变化(N+1)个电信号周期。不过，2种信号的相位差呈线性变化，在转子转过1周时，2种信号刚好相差1个周期。在转子转动过程中，2种信号的相位差始终小于1个电信号周期(2π)，即可以将相位差0～2π与机械角度0°～360°映射，然后再结合N或(N+1)传感通道的信号，实现绝对测量[15-16]。

由于2个传感通道共用感应线圈，所以2个传感通道的激励信号采用分时方式输入信号。该双传感通道传感器采用开关电路实现分时激励，首先将激励信号通入到N周期激励线圈，感应信号可用式(8)表示，然后将激励信号通入(N+1)周期激励线圈，感应信号可用式(9)表示。

(8)

(9)

通过两种信号的相位差，判断(N+1)周期信号在哪个变化周期后，即获取式(7)中的n后，再根据式(7)所示方式得到转子的绝对角位移。传感器在每次上电后，均需执行一次上述分时过程，得到起始绝对角位移。新的绝对角位移通过在起始绝对角位移上累加增量角位移得到。

3 模型仿真与分析

为了验证本文中传感器结构的可行性，利用三维建模软件对传感器进行模型建立，然后利用有限元仿真软件对模型进行仿真分析，主要仿真参数设置如表1所示。

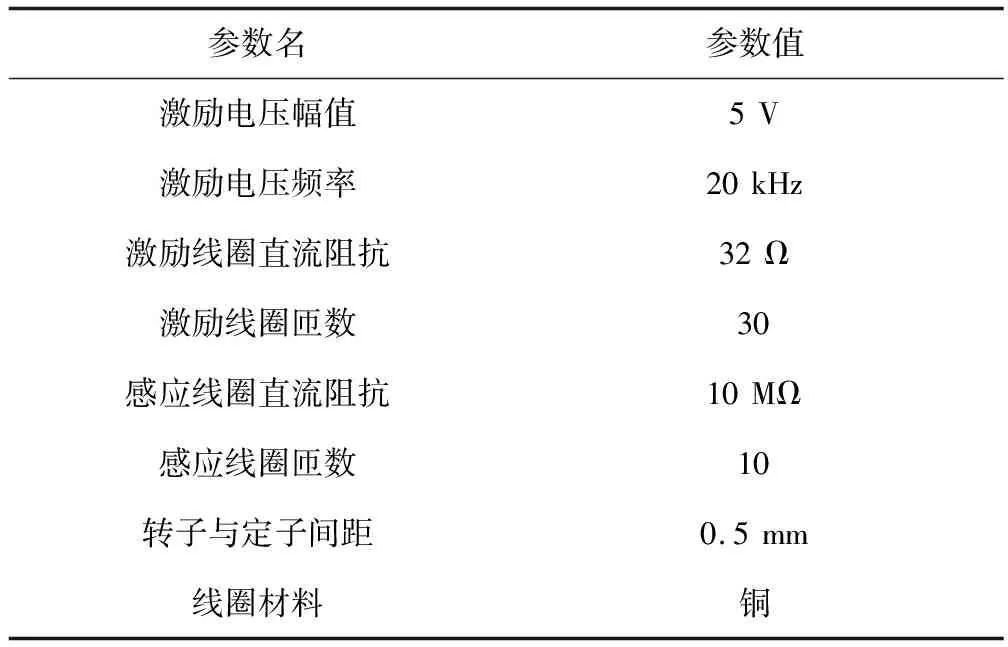
表1 主要仿真参数设置表

在仿真过程对计算机资源占用较大，且对计算机性能要求较高，因此在进行模型仿真设计时将模型设计为小而薄的低对极数传感器结构形式，但关键参数不予更改(仿真模型采用的重复结构周期数为9和10)。

转子在仿真过程中，9周期设置仿真步长为1.6°，在传感器的一个重复结构周期(40°)取25个位置进行仿真。10周期设置仿真步长为1.44°，在传感器的一个重复结构周期(36°)取25个位置进行仿真。在仿真过程中分别对9和10周期激励线圈通入单相激励e1和e2，得到的仿真结果分别如图4和图5所示。

提取图4和图5中单相激励的一组感应信号曲线，得到近似正弦的曲线，将其与标准正弦曲线相比，如图6(a)和图6(b)所示，感应信号具有较好的正弦性，与理论分析相符。

4 实验验证与误差分析

前文通过传感器的仿真分析过程，验证了传感器理论模型的可行性。在后续实验中，为了实现较高精度的测量，所研制的传感器样机的激励线圈采用重复结构为63和64的组合形式，感应线圈为相互串联的内外线圈，分别印制在同一块PCB上作为定子使用。转子和定子PCB如图7所示。

为开展实验研究，搭建了如图8所示的实验平台，以检测传感器样机的测量误差。该实验平台主要由待测传感器(定子基体、转子基体、定子PCB和转子PCB)、数据采集处理系统、转台驱动系统等几部分组成。

(a)9周期通入e1激励时的感应信号

(b)9周期通入e2激励时的感应信号

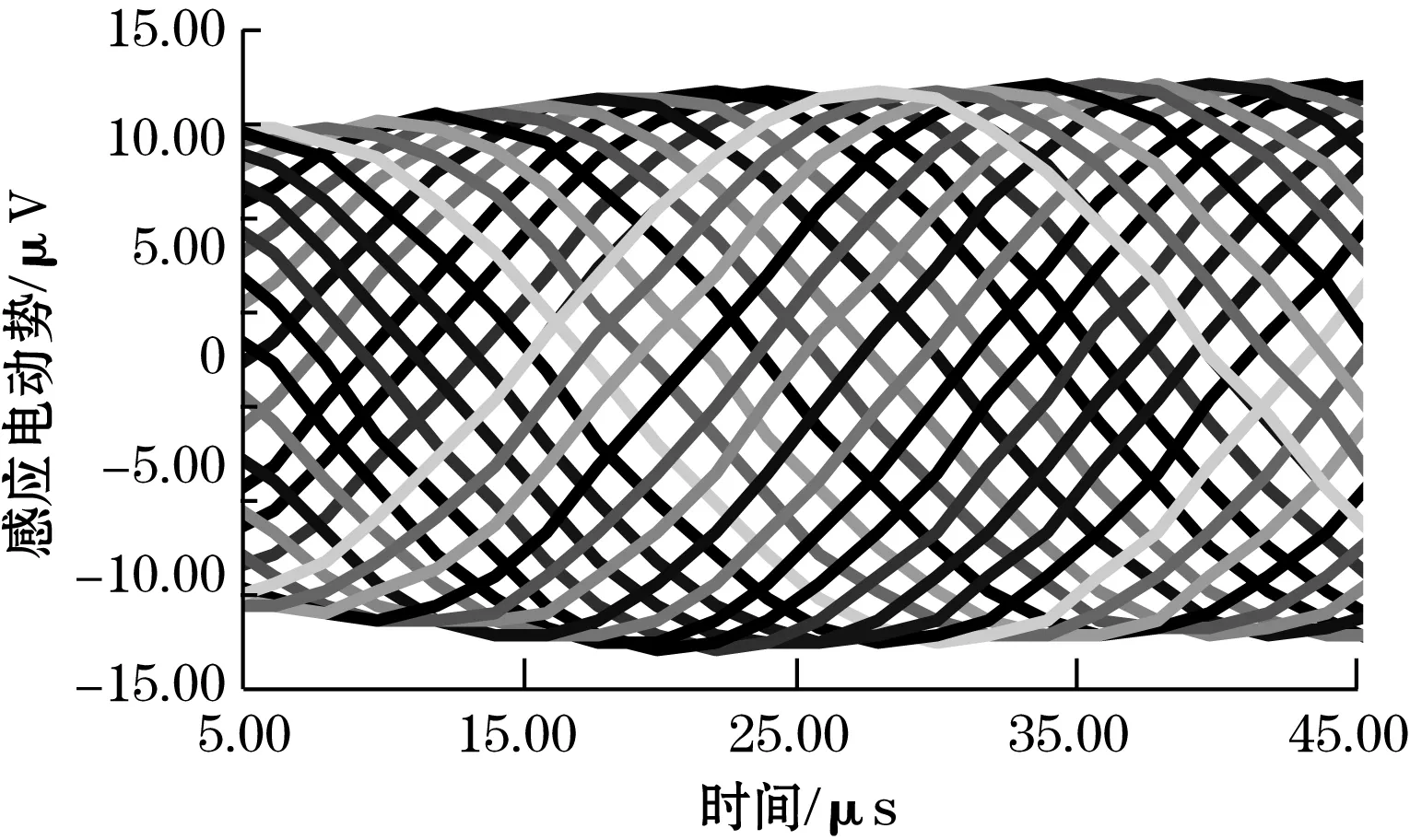
(c)9周期通入两相激励时的感应信号

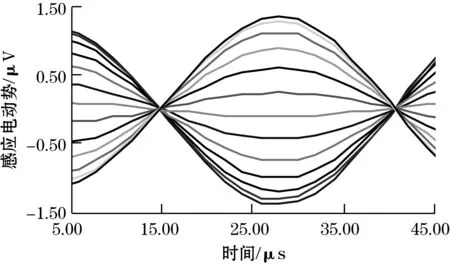
(a)10周期通入e1激励时的感应信号

(b)10周期通入e2激励时的感应信号

(c)10周期通入两相激励时的感应信号

(a)9重复周期电压幅值变化曲线

(b)10重复周期电压幅值变化曲线

图7 转子和定子PCB实物图

图8 实验测试平台

实验过程中，直驱转台带动光栅编码器输出的角位移量为测量基准。通过比对传感器样机和光栅编码器的测量数据，得到了传感器样机的原始测量误差。

在本文的研究中，分别对间隙为0.1 mm、0.2 mm、0.26 mm、0.48 mm、0.6 mm进行数据采样，实验数据如表2所示。通过数据分析，传感器存在明显的长周期一次误差，同时短周期误差呈现一定规律的变化。根据表2可得出结论，随着转子与定子间隙增加，长周期一次误差和短周期误差逐渐增大，且短周期二次误差逐渐明显。由于定子和转子的同心度不易调整，所以容易造成长周期一次测量误差。短周期高次测量误差通常是由于激励信号幅值不等、传感器结构或安装不对称造成的“磁场强度差”[15]、感应信号处理电路引入误差等原因造成。

最终选取定子转子间隙为0.2 mm进行详细测试。整周误差曲线如图9所示，横坐标代表0°～360°内的采样点，最大误差为28.8″，最小误差为-104.2″。短周期内误差曲线如图10所示，横坐标代表0°～5.625°内的采样点，周期内采样点为950个，最大误差为11.7″，最小误差为-74.5″。

图9 0.2 mm定、转子间隙时的整周误差曲线

图10 0.2 mm定、转子间隙时的短周期内误差曲线

5 结论

本文提出了一种基于PCB工艺的绝对式角位移传感器，采用PCB工艺实现了传感器所需的正弦形激励线圈和环形感应线圈，采用相差1个重复结构周期的双传感通道，实现了绝对式角位移测量。先后通过模型仿真和样机实验验证了该传感器的工作原理和结构可行性，最终获得传感器的整周原始误差在±70″范围内，短周期内误差 ±43″范围内。本文的研究对原始误差还未进行任何处理，若在后期的研究当中对传感器的原始误差进行消除，传感器的测量精度可以得到进一步提升。本文提出的传感器采用PCB工艺，不仅满足传感器对线圈形状的需求，而且为信号处理电路集中于传感器PCB提供了可能性，最终高集成化的传感器将适用于机器人关节臂等对传感器体积要求苛刻的工作场合。