不同网格加密方法在河流回补地下水模拟中的对比

崔伟哲，郝奇琛，陈 康，陈 飞，唐世南，朱玉晨，曹胜伟

(1. 河北地质大学 水资源与环境学院，河北 石家庄 050031； 2. 中国地质科学院水文地质环境地质研究所，河北 石家庄 050061； 3. 水利部水利水电规划设计总院，北京 100120)

0 引 言

为缓解地下水超采导致的地下水位下降和水资源枯竭等问题，很多国家实施了人工回补工程[1-3]。2019年5月，水利部印发了《2019年度河湖生态补水方案及试点河段后续补水计划》，明确根据南水北调、引黄、引滦等水源条件，向京津冀地区河湖生态补水约22.1×108m3，人工回补工程得到高度重视[4]。

地下水模拟是研究地下水运动的有效方法，可用来进行地下水回补模拟研究。国内外许多学者采用数值模拟的方法对人工回补过程、效果及优化问题进行了研究[5-10]，然而对于河流这种以线状回补模拟的精度问题很少提及。与面状回补模拟不同，河流附近网格剖分方式的不同将会对模拟结果产生影响，进而影响回补效果评估。

GMS(Groundwater Modeling System)软件及其内置的MODFLOW程序是地下水模拟的主流程序[11-13]，从10.0版本开始支持MODFLOW-USG(Unstructured Grid)程序，它是基于体积有限差分法(Control Volume Finite Difference,CVFD)对网格进行剖分[14]。相对于传统的MODFLOW程序，MODFLOW-USG程序可以对局部重点区域(如河流、开采井)进行非结构化网格加密，并且更加灵活。Krcmar等使用 MODFLOW-USG程序对斯洛伐克Gbely矿区进行模拟，精细刻画出与露天矿坑、构造断裂有关的地质非均质性[15]。Shokri等通过非结构化网格对地下水水力梯度较大的非承压含水层进行数值模拟[16]。苑希民等利用非结构化网格对黄河南岸灌区溃口等处进行局部加密模拟[17]。周念清等结合算例模型使用MODFLOW-USG程序对研究区域的源汇项、地下水位和流场分布进行数值模拟[18]。

非结构化网格加密方法包括四叉树网格(Q-tree Grid)、嵌套网格(Nested Grid)以及泰森多边形(Voronoi)，目前还没有专门针对回补模拟过程中不同网格加密方法精度与效果的对比研究。其中,泰森多边形法将网格剖分为不规则多边形，与其他两种规则矩形的剖分方法很难在网格剖分粗细上进行精确对比。为此，本文重点对比四叉树网格和嵌套网格加密方法，通过与两种结构化网格(粗、细结构网格)加密方法的模拟结果对比，分析线状回补模拟中不同网格加密方法的优劣，为地下水回补模拟加密方法选择提供参考。

1 非结构化网格加密方法简介

1.1 四叉树网格加密方法

四叉树网格加密方法最早应用在计算机领域，主要用于研究图像分割[19]。其原理是先将图像看成是一个正方形单元，如果该单元内有不同性质的多边形，则将单元分成4个大小相同的二级单元(图1)，这种逐级一分为四的方法一直继续到预定的最高分辨率[20]。Yerry等基于这一原理将四叉树网格加密方法应用于网格生成[21]。丁胜勇等利用四叉树网格加密方法对混凝土的界面过渡区进行局部网格加密，给出了更为合理的反映界面过渡区组分的混凝土细观模型[22]。

图1 四叉树网格和嵌套网格加密方法对比Fig.1 Comparison of Q-tree Grid and Nested Grid Refinement Methods

随着四叉树网格加密方法的不断改进，其应用领域也越来越广。2001年，英国牛津大学Rogers等首次将四叉树网格应用到二维潜水模型[23]。2002年，刘晓东等建立了基于四叉树网格的Godunov型二维水流数学模型，通过实验证明四叉树网格比传统结构网格在复杂流动区域的模型中具有更高的效率，计算值较精确[20]。2003年，华祖林等基于四叉树网格分层对重点污水排放区域进行模拟[24]。2020年，Bozovic等发现利用四叉树网格加密方法的区域地下水水力梯度最为明显，能较真实地刻画出地下水的三维流动[25]。

1.2 嵌套网格加密方法

嵌套网格是Mehl等开发的一种局部网格加密方法[26]。其原理是将模型分为子模型(加密区)和母模型(非加密区)两个独立的MODFLOW程序，通过一系列的迭代耦合，并在交界面传递水头和流量信息，实现模型嵌套[27-28]。

1994年，林振宝等基于FAC(Fast Adaptive Composite)方法，将全局粗结构网格解与局部细结构网格解之间交替迭代得到的局部加密嵌套网格应用到气藏数值模拟中[29]。1999年，孙雪梅提出了有限元单元网格加密方法，该方法只需要对模型所需部位的初始网格进行局部加密[30]。2013年，周巍等利用三层嵌套网格较精确地模拟了珠江口的主要水动力过程和盐度分布[31]。2015年，杨杨等对模型嵌套源代码进行二次开发，使得该程序可以对边界不规则的区域进行局部嵌套网格加密，在保证计算精度的情况下缩短了运行时间[28]。2017年，齐欢等通过GMS软件建立了趵突泉泉域的地下水流数值模型，利用嵌套网格加密方法对重点区域进行局部加密[27]。

1.3 非结构化网格加密的优势

在区域性地下水模型中，网格通常会剖分比较大[32]，在有开采井或河流这些水位变化明显的地方，模型不能很好地模拟出局部水位变化，这就需要对重点区域进行加密剖分。非结构化网格加密要比结构化网格加密更加灵活，在确保计算精度的情况下能有效减小计算量。韦未等通过两个算例证明局部网格加密可在确保计算精度的情况下,很大程度地减少计算量[33]。童少青等分别用结构化网格全区域加密和非结构化网格局部加密建立黑河中游盆地地下水流动模型，发现非结构化网格加密方法能够提高模型仿真度与计算结果精度[34]。

2 地下水回补算例模型

算例模型是根据水利部地下水管理与保护项目《河湖地下水回补试点补水效果》数值模拟中的拒马河模型概化而来。除模型范围外，算例模型中的水文地质结构、参数、边界条件等在概化过程中尽量保持与原始模型具有一定相似性，以求较为客观地反映实例情况。

2.1 算例模型建立

假设河流所在的区域面积为10 km×10 km的含水层，地下水总体流向为自西向东。根据研究区的水文地质条件，将含水层概化为非均质各向异性潜水、中层承压水、深层承压水等3层含水系统。其厚度分别为50、100、100 m，水平渗透系数分别为50、20、7 m·d-1，垂向渗透系数分别为0.08、0.04、0.02 m·d-1。含水层组间的水力联系强弱由模拟层间的垂向渗透系数控制。第1层给水度为0.08，第2层、第3层储水率均为0.000 1。东侧和西侧与外界存在明显的水量交换，将西侧设定为流量边界，东侧设定为给定水头边界，其他设定为通用水头边界。主要补给来源为大气降水，降雨强度为0.003 m·d-1。主要排泄项为人工开采，共布有9口开采井(图2)，其中6口井位于第1层，2口井位于第2层，1口井位于第3层，每口井的开采量设定为4 000 m3·d-1。模拟期为1年，半个月设置为一个应力期，1 d为一个步长。河道位于模型的第1层，河道的平均回补量设定为1.5×105m3·d-1，回补时间为1年。算例模型的水文地质结构、初始条件、边界条件等如图2所示。

图2 地下水回补算例模型结构及设置Fig.2 Structure and Setting for the Groundwater Recharge Model

2.2 4种网格剖分方案

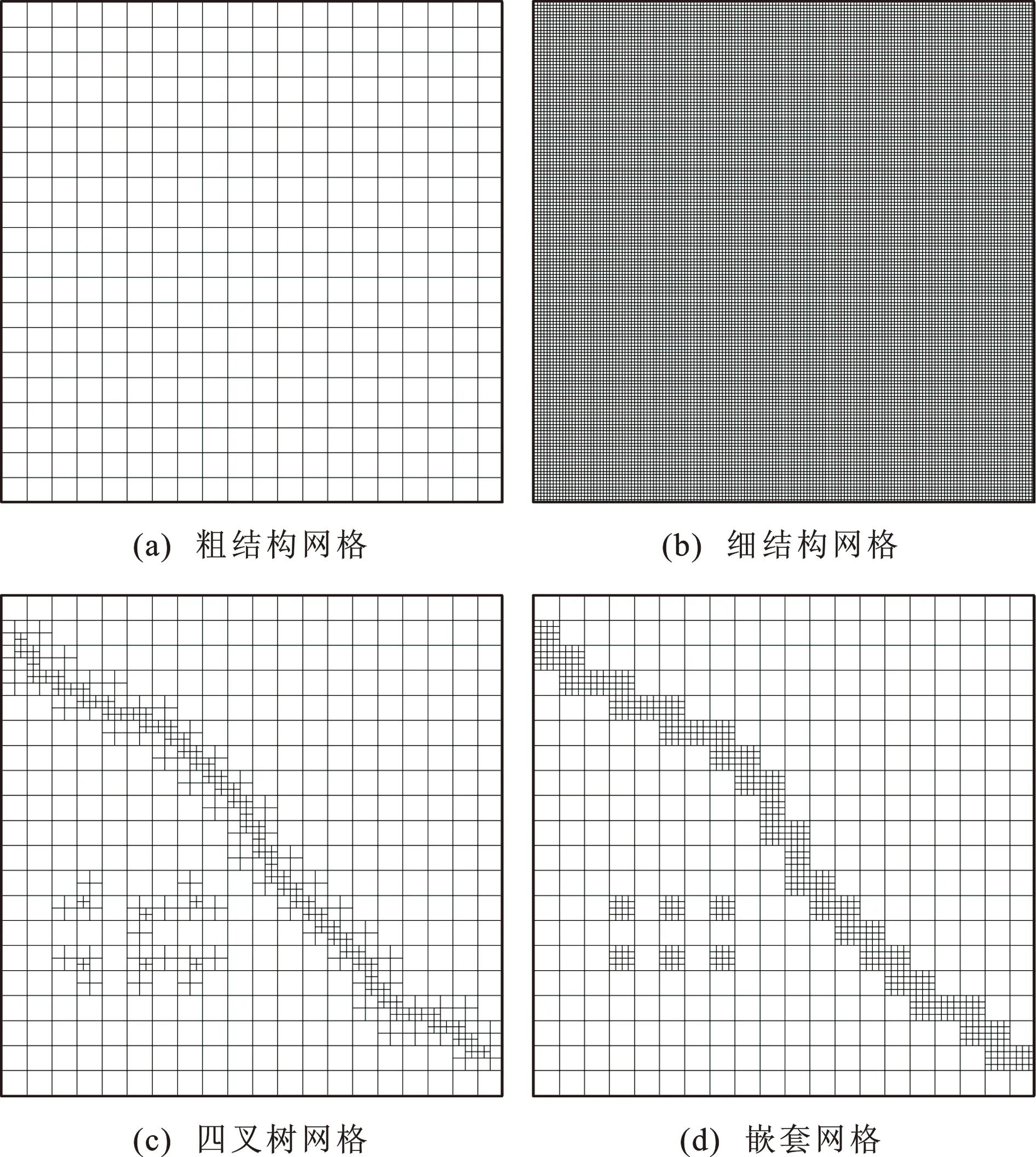
图3 4种网格剖分方案Fig.3 Four Grid Generation Methods

为对比不同加密方法的误差，共设置了4种网格剖分方案。方案一(粗结构网格)：网格剖分为500 m×500 m，网格数量为1 200[图3(a)]。方案二(细结构网格)：为尽量精细刻画地下水运动过程，网格剖分为15.625 m×15.625 m，网格数量为1 228 800[图3(b)]。方案三(四叉树网格)：局部河道处最小网格为125 m×125 m，由河道向两侧渐变为500 m×500 m，网格数量为2 586[图3(c)]。方案四(嵌套网格)：局部河道处网格大小为125 m×125 m，其他区域网格大小为500 m×500 m，网格数量为3 135[图3(d)]。

2.3 模拟情景

为了便于对比河流回补条件下的差别，设置了两种模拟情景，即无河道回补与有河道回补。两种情景中除有无河流回补的差别之外，其他条件均保持一致。以细结构网格模型作为标准模型，通过两种情景的模拟，对比研究不同网格加密方法对模拟结果的影响，包括末流场、水位及水量等方面，以此表征不同模型计算结果的精确程度[35]。

3 模拟结果分析及讨论

3.1 末流场对比

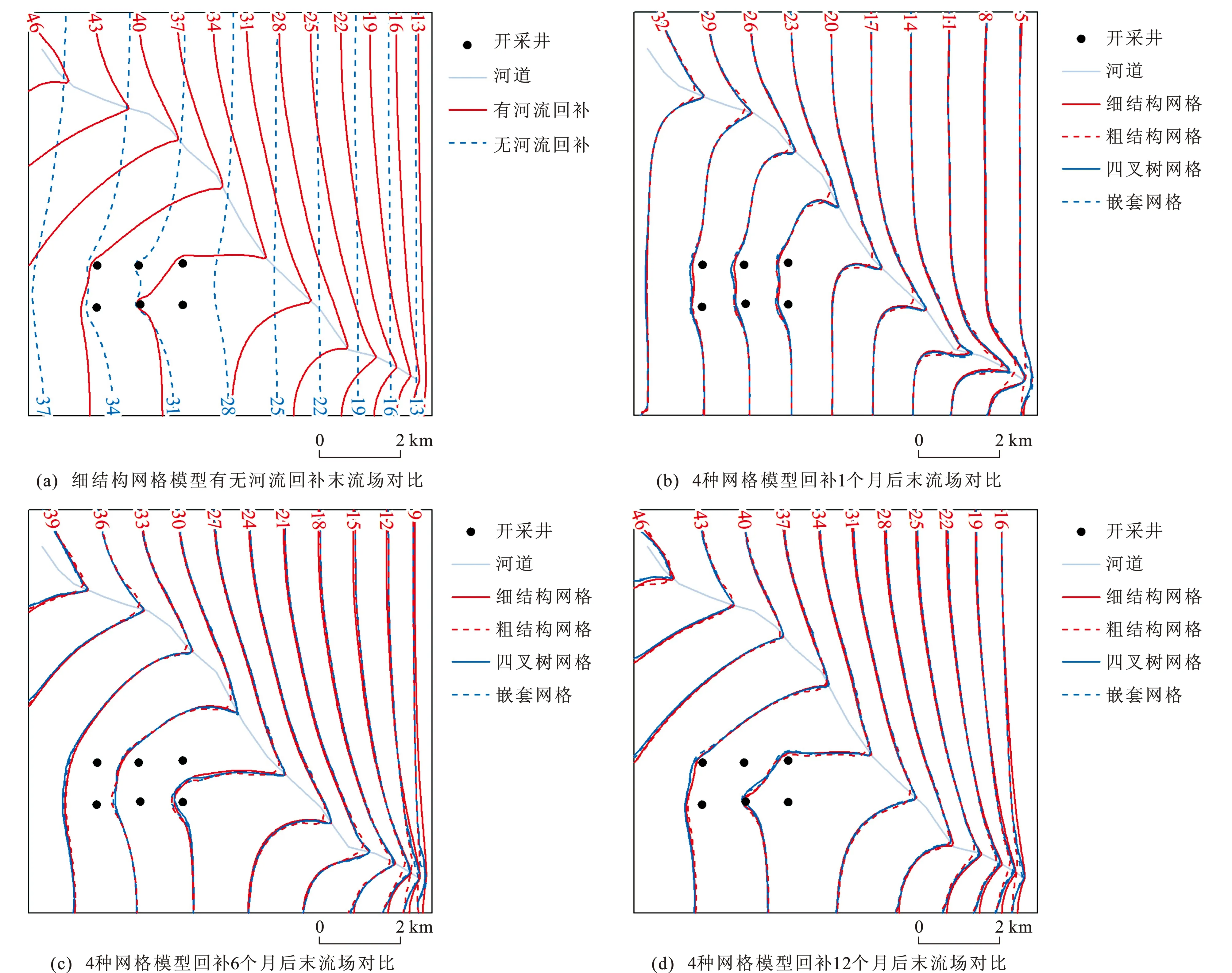
图(a)中数据为细结构网格模型的水位；图(b)、(c)、(d)中数据为4种网格模型的水位图4 模拟末流场对比Fig.4 Comparisons of Simulated Final Flow Fields

对比无河流回补与有河流回补条件下1年后细结构网格模型的浅层末流场[图4(a)]，可直观地看出在河流回补条件下，河道附近的水头值上升明显，回补效果较为显著。通过对比4种网格模型回补1个月、6个月、12个月后的末流场[图4(b)～(d)]可以看出，整体上4种网格剖分方案模拟的末流场大体一致，大部分地区等水位线基本重合，但在河道附近，模拟的末流场形态有一定差异，特别是回补初期，粗结构网格模型的误差较大。随着回补时间的延长，河道附近的误差变小，但远离河道的区域开始出现一定的误差，特别是在边界处。

为能更精确地看出网格模型之间的末流场差异，采用定量化评价指标，以细结构网格模型的末流场为标准，计算出位于河道500 m范围内粗结构网格、嵌套网格、四叉树网格模型与标准网格模型末流场的标准差(表1)。河流回补1个月后，粗结构网格模型的标准差要比其他两种非结构化网格模型大0.2左右。回补12个月后，粗结构网格模型的标准差与四叉树网格模型的差距依然保持在0.2以上，而与嵌套网格模型的标准差差距逐渐降为0.14。在整个回补过程中，与粗结构网格模型相比，两种非结构化网格模型的末流场都要更接近标准末流场。而随回补时间的增加，四叉树网格模型与嵌套网格模型的标准差也在逐渐拉大，回补12个月后四叉树网格模型的标准差要比嵌套网格模型小0.07。从两种非结构化网格模型的标准差对比来看，在回补期末，四叉树网格模型的末流场要比嵌套网格模型更接近标准末流场。

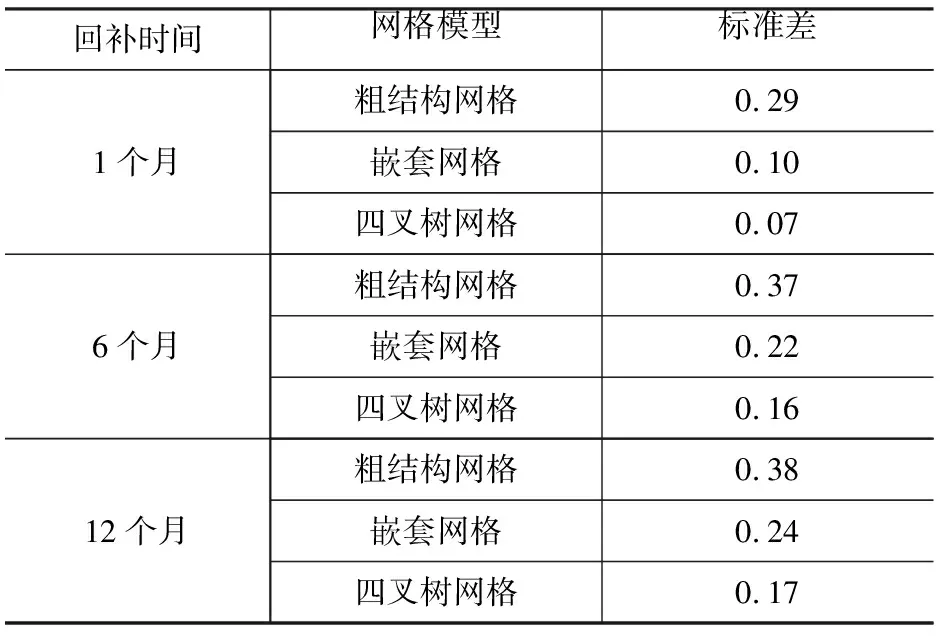
表1 不同网格模型标准差对比

根据上述结论，统计出位于河道500 m范围内两种非结构化网格模型与标准网格模型的3期(回补1个月、6个月、12个月)误差，并统计出误差所占的比例分布(图5)。河流回补1个月后，两种非结构化网格模型的误差基本都保持在0.1 m内(分别为98.83%、99.77%)。随着回补时间的增加，两种非结构化网格模型的误差在0.1 m以上的比例也都在逐渐增加。回补6个月后，嵌套网格模型在误差为0.5 m以上的比例是四叉树网格模型的2.7倍，并且此时嵌套网格模型已经开始出现误差大于1 m的区域，四叉树网格模型从回补初到回补末，误差一直保持在1 m内。这也能够解释随着回补时间的增加，四叉树网格模型与嵌套网格模型的误差差距逐渐变大的原因，同时也进一步说明四叉树网格模型在长期模拟过程中的优势。

3.2 水位相对上升差异

3.2.1 4种网格剖分方案对比

图6为4种网格模型回补条件下的水位相对上升情况(上升值为同一种剖分方式下，有回补条件下模拟的末流场水位减去无回补条件下模拟的末流场水位)。整体上看，4种网格剖分方案的模拟结果大体一致，水位上升范围沿河道呈条带状分布，最远影响距离约为5.9 km(以水位变差1 m计算)，回补河段上游影响距离较大。

从形态上看，粗结构网格模型的模拟结果与其他3种网格模型的模拟结果有一定差异，主要表现为等水位线不够圆滑，下游一端的梭形形态未体现出来。细结构网格模型与其他两种非结构化网格模型的模拟结果较相似，形态较圆滑。

从最高变幅看，粗结构网格模型的模拟结果与其他3种网格模型也有较大差别。细结构网格模型的最大水位变幅约为9 m，且呈条带状分布在河道两侧，9 m等水位线圈闭的面积为0.74 km2，其他两种局部加密的非结构化网格模型模拟结果也类似，9 m等水位线圈闭的面积分别为0.68、0.66 km2；但粗结构网格模型的9 m等水位线圈闭的面积只有0.33 km2，相比细结构网格模型小了55%，且圈闭范围不连续，甚至8 m等水位线也不圈闭。

综上所述，相比粗结构网格模型，其他3种网格模型均能有效提高模拟精度，但三者也略有差别，以下将从不同距离的水位变差、单个观测孔的水位过程线以及均衡情况进一步论述。

为了更直观体现不同方案的差别，统计出4种网格剖分方案中距离河道30～800 m的水位变差(图7)。从整体变化趋势上看，4种网格模型的水位变差变化趋势基本相同。随着与河道距离的增加，水位变差不断减小，受河流回补影响越来越小，同时水位变差速率也逐渐减小。但在距河道300 m范围内，粗结构网格模型的模拟结果与其他3种网格模型有较大差别。在距离河道30 m范围内，细结构网格模型的水位变差约为8.41 m，两种局部加密的非结构化网格模型模拟结果与其较接近，分别为8.21、8.17 m，而粗结构网格模型的水位变差只有7.89 m，比细结构网格模型小6%。在回补效果评估过程中，这种差异一定程度上会导致评估效果的不准确。

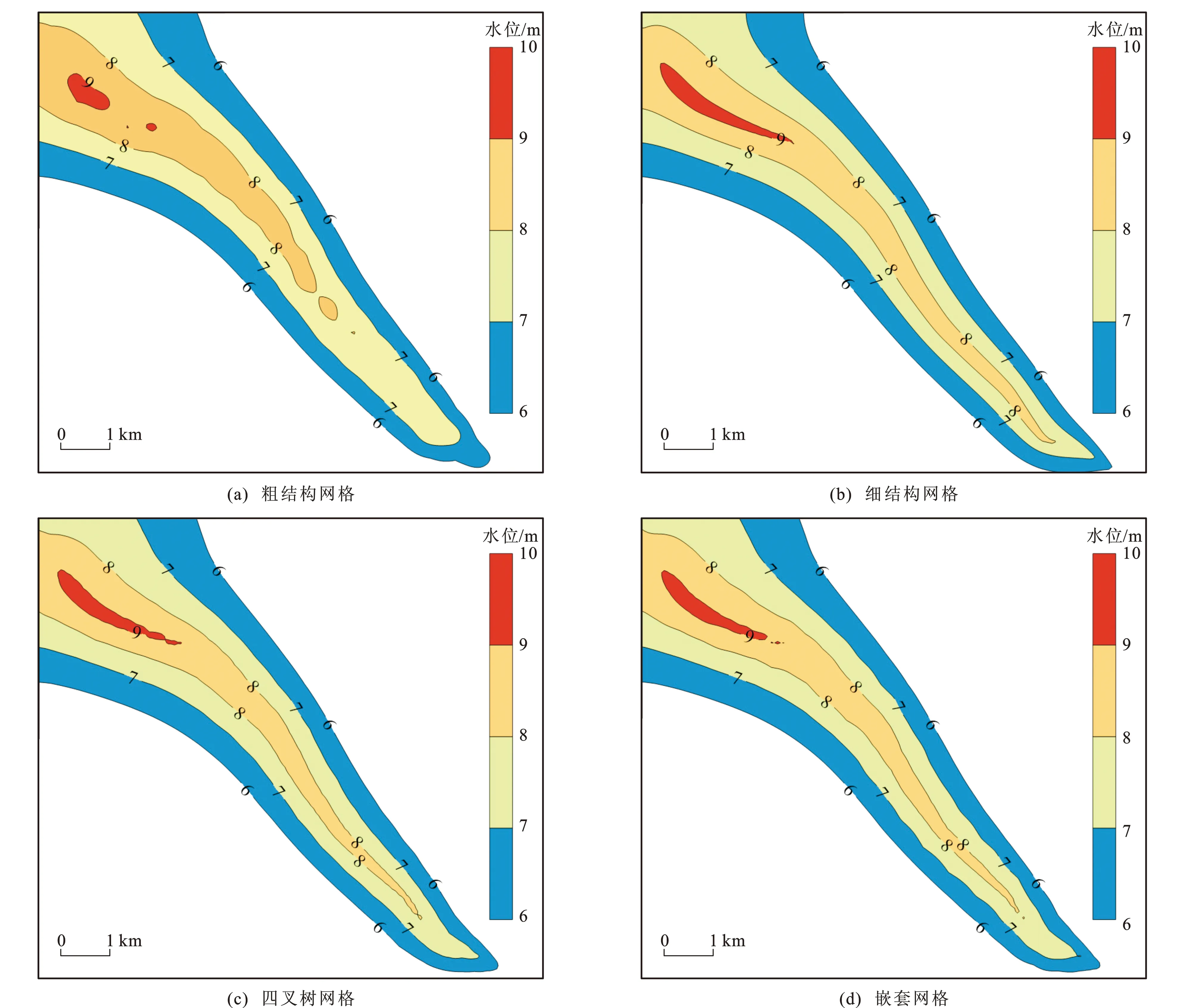
图6 回补条件下的水位相对上升情况Fig.6 Relative Increases of Water Level Under Recharge Conditions

图7 距离河道不同范围的水位变差对比Fig.7 Comparison of Water Level Variations Under Different Distances with River

在距离河道上游100 m、中游200 m处设置两个观测孔(图2)，对比4种网格模型的地下水位动态(图8)。两种局部加密的非结构化网格模型与细结构网格模型的水位动态更接近。在回补期末，距离河道100 m观测孔的细结构网格模型的水位变差要比粗结构网格模型的水位变差高1.21 m。从时间变化来看，随着时间的推移，受河道回补的影响，水位逐渐升高，升高速率逐渐变缓，但4种网格模型的水位变差的差距却在扩大。从距离河道不同范围的观测孔来看，距离河道200 m观测孔的4种网格模型的水位动态差距要小于距离河道100 m处的观测孔。

距离河道不同范围的水位变差对比(图7)综合分析表明：在有河道回补的地下水模型中，河道所在网格剖分较粗时，由回补引起的附近水位变化会被平缓化，在模型中表现不突出；当对河道所在网格进行加密后，河道所在网格体积减小，其附近网格数量相对增加，地下水位的变化受河道回补影响也就更加明显；局部加密的非结构化网格模型能够更加精细刻画出局部的水位变化。

图8 距离河道100、200 m观测孔水位动态对比Fig.8 Comparisons of Water Level Change for Observation Wells Under the Distances of 100 and 200 m with River

3.2.2 不同边界条件对误差的影响

边界条件是数值模拟中一项重要设置，以上研究结果都是基于西侧补给区边界为二类边界(流量边界)得出的，因此，需要通过改变不同的边界条件来分析其对误差的影响。在补给区改用一类边界(给定水头边界)、三类边界(通用水头边界)，模型的其他条件或参数均保持不变。以细结构模型在距离河道不同范围的水位变差为标准，分别计算出不同边界条件下，其他3种网格模型模拟的水位变差与细结构网格模型之间的误差(图9)。

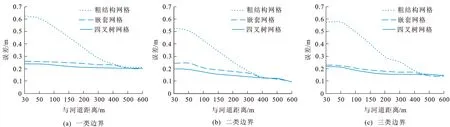
图9 不同边界条件下水位变差的误差对比Fig.9 Comparisons of Water Level Variation Errors Under Different Boundary Conditions

3类边界条件下，3种网格模型之间的误差变化趋势基本相同。距离河道30 m处，粗结构网格模型的误差均在0.5 m以上，两种非结构化网格模型的误差相对较小，保持在0.2～0.3 m；随着与河道距离的增加，粗结构网格模型与非结构化网格模型的误差逐渐减小，距离河道400 m后，3种网格模型的误差基本趋于一致。这说明不管在什么边界条件下，非结构化网格模型的模拟精度都要高于粗结构网格模型。同时，从整体上看，3类边界条件下，四叉树网格模型的误差要比嵌套网格模型偏小0.01～0.04 m，模拟精度要稍高于嵌套网格模型。

3.2.3 不同加密级次对误差的影响

四叉树网格模型河道附近最小网格为125 m×125 m，最大网格为500 m×500 m，属于三级加密。将其改为六级加密，局部最小网格剖分为15.625 m×15.625 m(网格数量为15 771)，同时将嵌套网格模型的最小网格也剖分为15.625 m×15.625 m(网格数量为133 167)。进一步加密后的模型参数与之前的参数均保持一致，对比非结构化网格模型与标准网格模型在距离河道不同范围的水位变差(图10)。

从模拟精度上看，进一步加密后的四叉树网格模型和嵌套网格模型在距离河道30 m处的水位变差相对于之前的模型分别仅增加了0.04 m和0.03 m，模拟精度提升不大。在距离河道300 m后，非结构化网格模型的水位变差基本保持一致。

考虑到模型的网格数量，进一步加密后的嵌套网格模型网格数量要比之前高42倍，四叉树网格模型网格数量也要比之前高6倍。显然，为提高模拟精度再次加密局部网格的非结构化网格模型意义不大。另外，对局部网格再次加密后，嵌套网格模型要比四叉树网格模型的网格数量多7倍，再次说明四叉树网格模型具有多级加密且级次越多，优势越明显的特点。

图10 网格加密前后在距离河道不同范围的水位变差对比Fig.10 Comparison of Water Level Variations Before and After Grid Refinement Under Different Distances with River

3.3 地下水侧向径流量变化

在河道两侧200 m范围建立均衡区，对比第2.2节中4种网格剖分方案回补期末均衡区内的侧向径流量(表2)。从表2可以看出，细结构网格模型与两种非结构化网格模型的模拟结果较为接近，但这3种网格模型与粗结构网格模型的模拟结果差异较大，粗结构网格模型比细结构网格模型的侧向径流量少约15%。上述结果进一步验证了前述论证，即回补模拟过程中，粗结构网格模型的水位升高值要比其他3种网格模型低，故水力梯度也小，最终导致侧向径流量明显偏小。

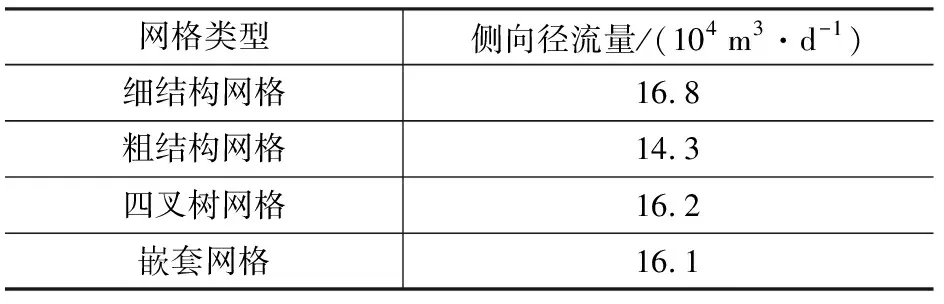
表2 4种网格剖分方案侧向径流量对比

3.4 模型运行效率

在实际应用中，地下水模型运行效率尤为重要。由于软件本身和计算机能力的限制，在建模过程中，当网格数量过多时，很容易出现模型运行效率低下甚至无法运行的情况，给局部网格加密带来很大困难。本次研究模型为前述建立的河流回补模型，对4种网格剖分方案的运行效率进行了对比分析，采用的计算机CPU为4核1.8 GHz，RAM为8 GB。计算结果如表3所示。

细结构网格模型相对于粗结构网格模型进行了全区域整体加密，在模拟结果上更精确，但由于剖分的网格数量过多，运行时间高达5 h，并且运行后会产生40 GB的结果文件，占据了大量计算机存储空间。两种非结构化网格模型只是在河道附近区域进行局部加密，相对粗结构网格模型，网格数量增加不大，由1 200分别增加到2 586和3 135，运行时间有一定程度的增加。另外，两种非结构化网格模型之间相比较，四叉树网格模型(三级加密)要比嵌套网格模型(局部为125 m×125 m)节省18%的运行时间。这是由于嵌套网格模型是对河道所在区域均匀加密，而四叉树网格模型采用的是渐变网格剖分方法进行局部加密，网格数量相对较少。四叉树网格模型(六级加密)的运行时间仅是嵌套网格模型(局部为15.625 m×15.625 m)的15%，节省了85%的运行时间，具有多级加密的优势。

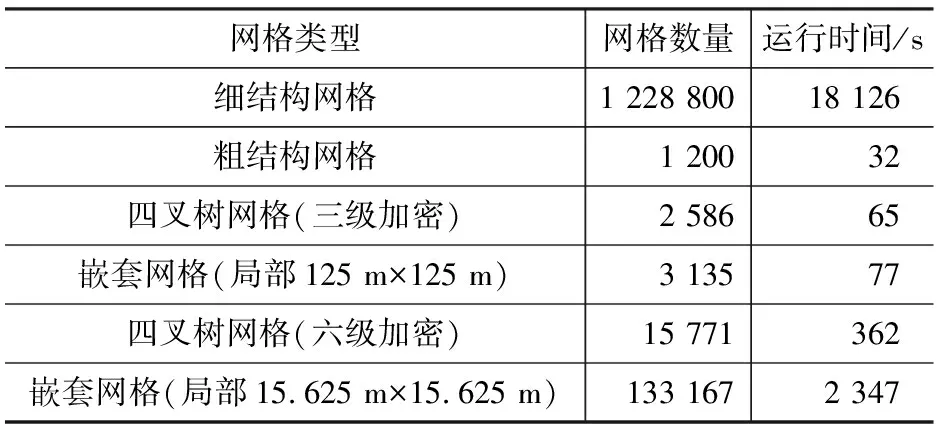
表3 不同网格剖分方案运行时间对比

4 结 语

(1)通过对比分析不同网格剖分方案下模拟的末流场、距离河道不同范围回补前后水位变差、单个观测孔的水位过程线、均衡情况、模型运行效率等，表明两种局部加密的非结构化网格模型以及细结构网格模型比粗结构网格模型的模拟精度高，更能准确刻画因河道回补导致的地下水位变化。对于长期模拟的模型而言，四叉树网格模型相对于嵌套网格模型更具优势，且适用于不同类型的边界条件。

(2)两种局部加密的非结构化网格模型比细结构网格模型网格数量少，运行时间短，在没有大幅降低模拟精度的前提下，运行效率更高，且四叉树网格模型具有多级加密的优势，加密级次越多，优势越明显，运行时间相对更短。

(3)在模拟河流生态补水对地下水影响时，四叉树网格加密方法的模拟精度和运行效率相对较高，具有一定优势，是值得推荐的一种局部网格加密方法。