基于GAPSO-RBFNN的动车组电机吊架多目标稳健优化设计

李永华，盛自强，宫 琦

（1.大连交通大学 机车车辆工程学院,辽宁 大连 116028；2.大连交通大学 机械工程学院,辽宁 大连 116028）

高速动车组电机吊架主要承担着连接牵引电机、并将其弹性安装在转向架构架上的作用,是CRH3型动车组牵引电机悬挂装置的重要组成部分,因此电机吊架的性能稳定性对动车组的走行安全具有十分重要的意义。为了降低电机吊架质量特性对外界不可控因素的敏感性,增强电机吊架性能在制造和运用过程中的抗干扰性,对电机吊架进行稳健设计十分必要［1］。目前,稳健设计的有效性已经在各个领域的工程实践中得到很好的应用验证［2-5］,并且诸多学者的研究是在参数建模的基础上实现的稳健优化。参数建模虽然具有较高预测精度和便于数学解析的优点,但是在实际工程应用中会受到模型参数假设和设计者经验知识造成的误差影响,使参数模型的解难以保证收敛于真实解的分布。为了克服参数模型的上述不足,考虑构建电机吊架各质量特性信噪比的非参数模型。非参数建模无需过多的先验知识和模型参数假设,能够更加真实地反映设计参数与目标响应之间的映射关系,因而在解决复杂工程问题中得到广泛的应用［6-8］。

径向基函数神经网络（Radial Basis Function Neural Network,RBFNN）是一种学习效率高,泛化能力强的非参数模型［9］。卫晓娟等［10］基于RBFNN 建立机车齿轮箱的故障诊断模型,并结合自适应混合引力算法对其求解,有效地提高了齿轮箱故障诊断的效率。王春林等［11］利用RBFNN 拟合渣浆泵设计参数与优化目标间的映射关系,构建出渣浆泵的优化模型,通过求解优化模型得到渣浆泵的最优设计参数。Mohammed 等［12］利用K-均值聚类算法改进RBFNN 来预测太阳能电池板的输出功率,使得输出功率的预测值达到可接受的精度。Othman 等［13］将RBFNN 应用于电力系统的短期负荷预测,为电力系统的管理提供了数据支撑。然而上述研究多是直接将RBFNN 用于确定性优化设计或者是数据预测,目前鲜有将RBFNN 应用于多目标稳健优化设计的研究报道,并且上述研究忽略了平滑系数对RBFNN模型精度的影响。

本文基于遗传粒子群算法（GAPSO）获取最优平滑系数以提高RBFNN 的预测精度,进而得到GAPSO 改进的RBFNN,并将其应用于电机吊架的多目标稳健优化模型的构建。采用NSGA-II多目标优化算法对稳健优化模型进行寻优计算,得出电机吊架的稳健设计方案,并与传统设计方案进行对比。

1 基于GAPSO算法改进RBFNN

1.1 RBFNN

RBFNN 是一种3 层前向型网络,可以近似任意的非线性连续函数,分为输出层、隐含层和输入层。RBFNN 的具体思路为：用径向基函数作为隐含层神经元的“基”构成隐含层空间,完成由输入层到隐含层空间非线性映射［14］。最常用的径向基函数为高斯函数,其具体描述为

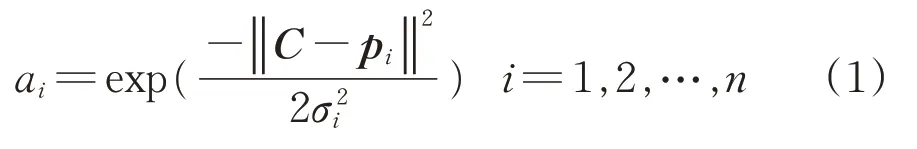
式中：ai为隐含层第i个神经元的输出；pi为第i个输入样本向量,pi=(pi1,pi2,…,pim)；C为径向基函数中心,维数与pi相同；σi为高斯函数的宽度参数,即平滑系数；n为隐含层神经元个数；m为输入样本维数。

RBFNN 的输出为隐含层输出的线性加权和,则RBFNN输入与输出之间的关系可表示为

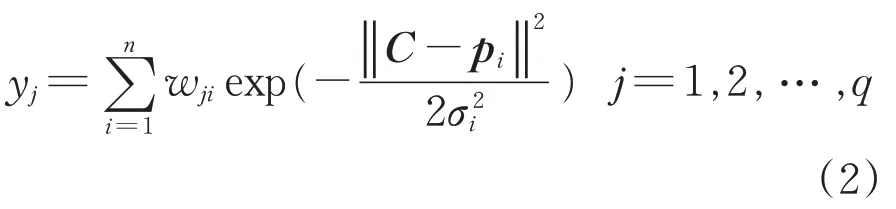
式中：yj为输出层第j个神经元的输出值；wji为隐含层第i个神经元与输出层第j个神经元之间连接的权值；q为输出层神经元数量。

1.2 GAPSO-RBFNN

平滑系数是对RBFNN 预测精度起着至关重要作用的参数。平滑系数控制着高斯函数的平滑度,过大或过小的平滑系数都会导致RBFNN 预测性能的降低。文献［15］的研究已表明,对于不同的训练样本,RBFNN 对应不同的最优平滑系数,且RBFNN平滑系数通常人为设定,这会导致RBFNN预测性能在实际应用中无法达到最优。

遗传算法（Genetic Algorithm,GA）和粒子群算法（Particle Swarm Optimization,PSO）都是采用一定的仿生变换规则在解空间中搜索寻优的群体智能优化算法［16-17］。为了改进粒子群算法的全局搜索能力,在粒子群算法中引入遗传算法,编写GAPSO 算法,进行RBFNN 平滑系数的寻优计算。GAPSO-RBFNN 的主要步骤为：将RBFNN初始平滑系数编码得到初始化种群；对初始化种群执行GAPSO 算法,直至满足GAPSO 算法的终止条件；输出最优个体对应的平滑系数并赋给RBFNN,训练得出最优RBFNN。GAPSO-RBFNN的详细流程如图1所示。

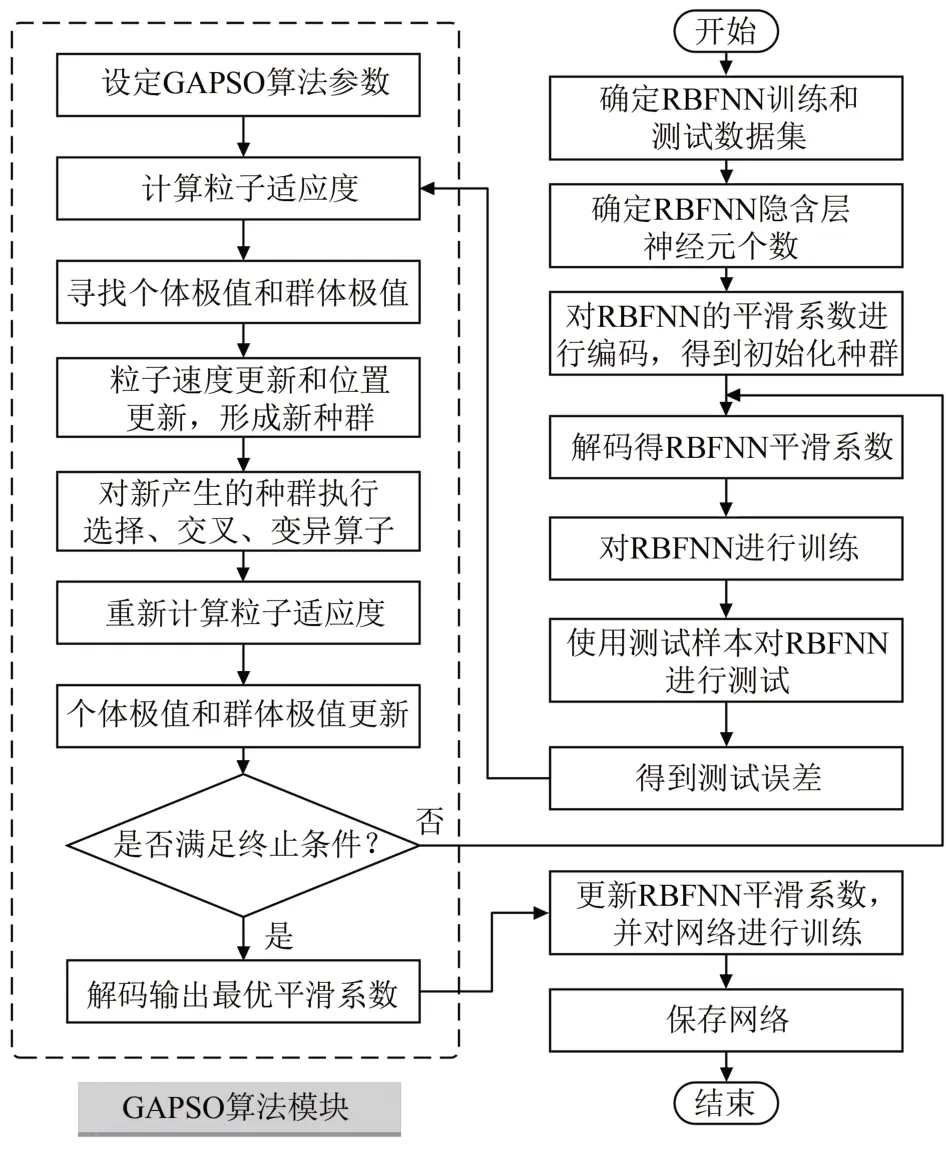
图1 GAPSO-RBFNN构造流程图

对于每个粒子的适应度函数fit采用网络预测输出与期望输出的标准差表示,为

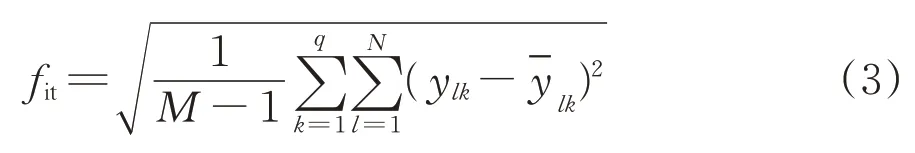
式中：M为样本数据的个数；ylk为第l个样本通过神经网络的第k个预测输出；为对应的期望输出。

式（3）中,适应度越小代表该粒子越优。

2 基于田口稳健设计理论的电机吊架稳健性衡量

采用田口稳健设计中的信噪比衡量电机吊架多质量特性的稳健性,信噪比越大表示电机吊架性能越稳健［18］。常用的信噪比有望目特性、望大特性和望小特性3种类型［1］。

在电机吊架的多目标稳健优化中,选取电机吊架总质量和自然频率衡量电机吊架质量特性,并以其为研究对象。对于电机吊架总质量,期望在一定范围内越轻越好,具有望小特性。因此,电机吊架总质量信噪比SN1［1］为

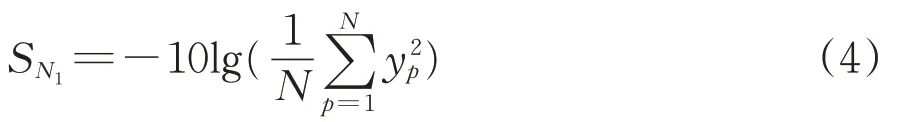
式中：yp为第p次试验的电机吊架总质量的质量特性值；N为试验次数。

牵引电机转速与车辆行驶速度间关系［19］为

式中：ω为电机转速,r·min-1；z为牵引齿轮传动比；D为车轮直径,m；v为车辆运行速度,km·h-1。

由相关资料［20］可知z=2.429,D=0.92m,CRH3型动车组最高运行速度为300 km·h-1。由式（5）可计算出牵引电机工作转速范围为0～4 202 r·min-1,其对应工作频率区域为0～70.03 Hz［21］。对电机吊架进行动力学仿真分析可知其自然频率（1 阶模态频率）为70.06 Hz,与电机工作频率相近,易产生共振现象从而影响电机吊架使用寿命。为了避免电机吊架发生共振,期望其自然频率远离电机工作频率区域,即电机吊架自然频率应高于牵引电机工作频率区域的上限点,故电机吊架自然频率具有望大特性,其信噪比SN2［1］为

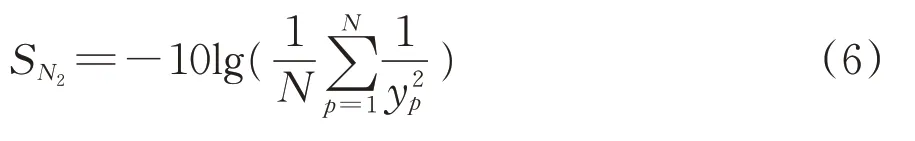
3 电机吊架多目标稳健优化设计

3.1 电机吊架灵敏度

电机吊架结构由10 种不同厚度的板件焊接而成,因而进行电机吊架多目标稳健优化设计时选取10 种板件厚度作为设计变量。为了提高优化设计效率,需要进行10 种板件厚度对总质量和自然频率的灵敏度分析,根据分析结果筛选出关键设计变量。

进行电机吊架的灵敏度分析,需要建立其有限元模型,如图2所示。电机吊架整体采用Shell181单元进行网格划分,网格大小为10 mm,共计30 176 个节点,单元总数为50 879 个,采用Rbe3刚性单元模拟螺栓连接。

利用软件HyperWorks 14.0 的Optistruct 模块进行各板厚对所选质量特性的灵敏度分析,分析结果见表1,电机吊架各板厚灵敏度分析柱状图如图3所示。

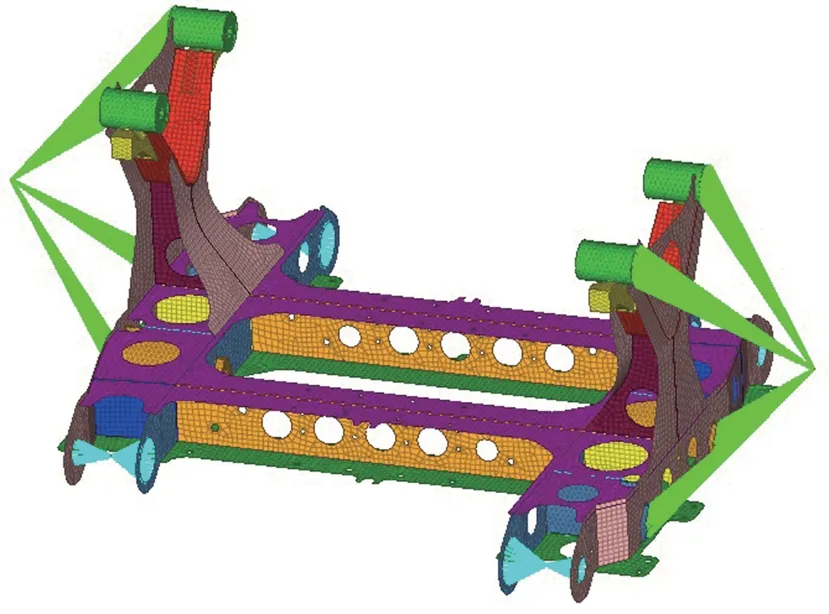
图2 电机吊架有限元模型

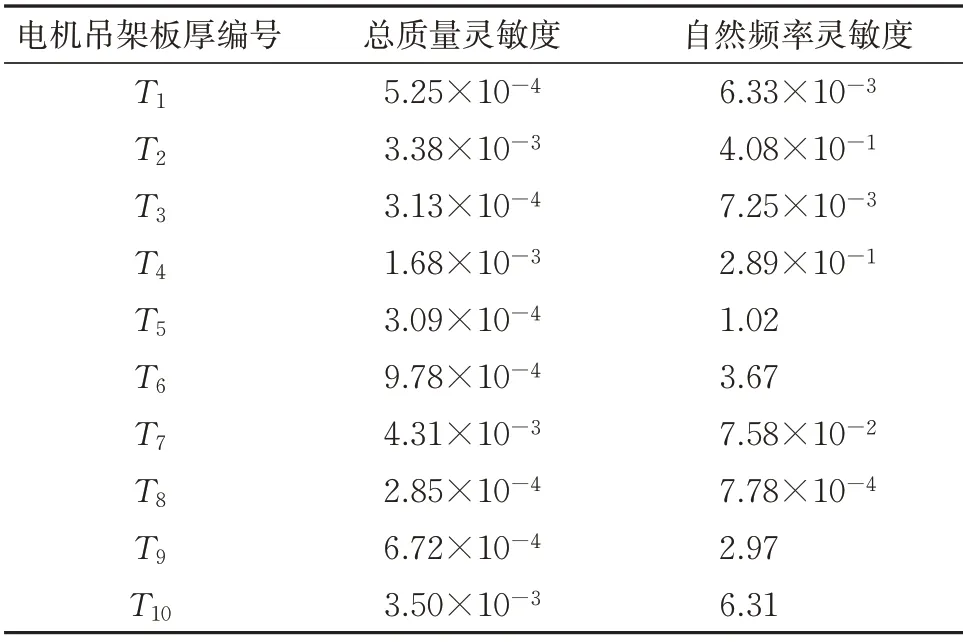
表1 电机吊架板厚灵敏度计算值

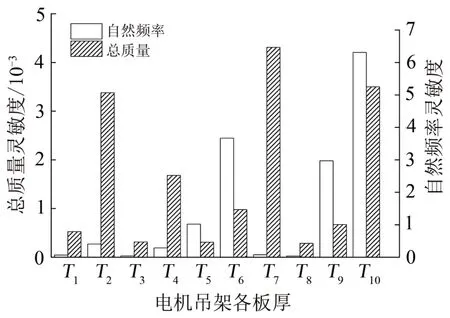
图3 电机吊架各板厚灵敏度柱状图

根据图3可以看出：T10,T9和T6对电机吊架总质量和自然频率都比较敏感,即T10,T9和T6的增加,均会导致总质量和自然频率的显著增加；虽然T2,T4和T7对自然频率的增加作用不够明显,但是增加这些变量会使总质量明显增加。综上分析,选择T2,T4,T6,T7,T9和T10作为关键设计变量。

3.2 电机吊架多目标稳健优化设计模型

3.2.1 影响因素

田口稳健设计将影响产品质量的因素归为可控因素和不可控因素2类［1］。

可控因素是指电机吊架在设计和制造过程中可以控制的因素。由3.1 节的灵敏度分析可知,在电机吊架的稳健设计时将选择板厚T2,T4,T6,T7,T9和T10作为可控因素；不可控因素是指对电机吊架质量特性有影响而在设计和生产时难以控制的因素,确定为弹性模量E和密度ρ。根据电机吊架的设计要求确定出可控因素和不可控因素的水平值,其中可控因素取三水平值,不可控因素取两水平值,其具体数值见表2。

3.2.2 构建多目标稳健优化模型

为了获得较高拟合度的RBFNN,需先通过田口正交试验设计获取神经网络的训练和测试数据样本。

田口正交试验设计需要建立内表和外表2个正交表［1］。内表用于安排可控因素,外表用于安排不可控因素。试验有6 个三水平可控因素,2 个两水平不可控因素,故内表选用正交表L27(36),外表选用正交表L4(22)。以电机吊架总质量和自然频率为观测目标,试验共计216个观测值。

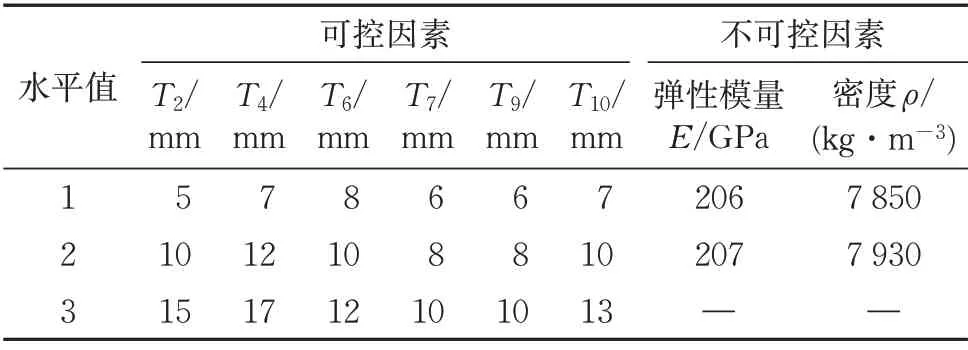
表2 电机吊架各影响因素及其水平值

总质量和自然频率的信噪比分别按照式（4）和式（6）计算。受篇幅限制,各质量特性信噪比部分计算结果见表3。

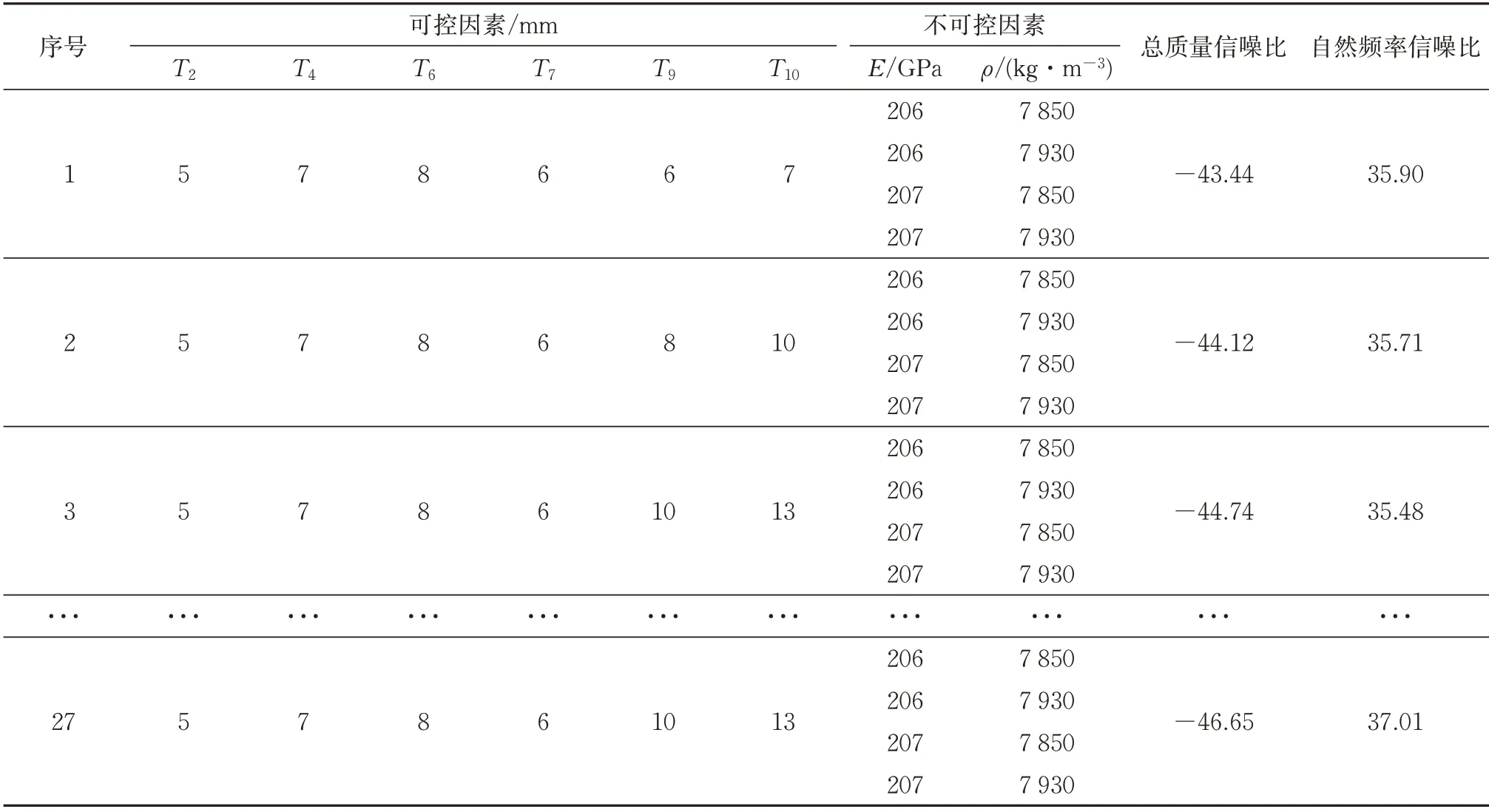
表3 各质量特性信噪比

通过上述田口正交试验设计,获取了27组数据样本。以各质量特性信噪比作为GAPSO-RBFNN的输出,随机选取其中20组数据作为RBFNN模型的训练样本,另外7 组作为其测试样本。GAPSO算法参数设置见表4。

表4 GAPSO算法参数设置

将测试样本代入训练好的GAPSO-RBFNN 模型进行测试,并将其预测结果与传统RBFNN 的预测结果进行对比,如图4所示。

为了量化比较GAPSO-RBFNN 和RBFNN 的预测精度,计算2 种网络模型的预测输出与期望输出的相对误差,其结果见表5。

由图4和表5可以得出,GAPSO-RBFNN 的总质量信噪比平均相对误差为0.056%,自然频率信噪比平均相对误差为0.161%；而RBFNN 的总质量信噪比平均相对误差达到了0.205%,自然频率信噪比平均相对误差为0.473%。通过上述分析可以看出,GAPSO-RBFNN 的预测精度相比于RBFNN显著提升。

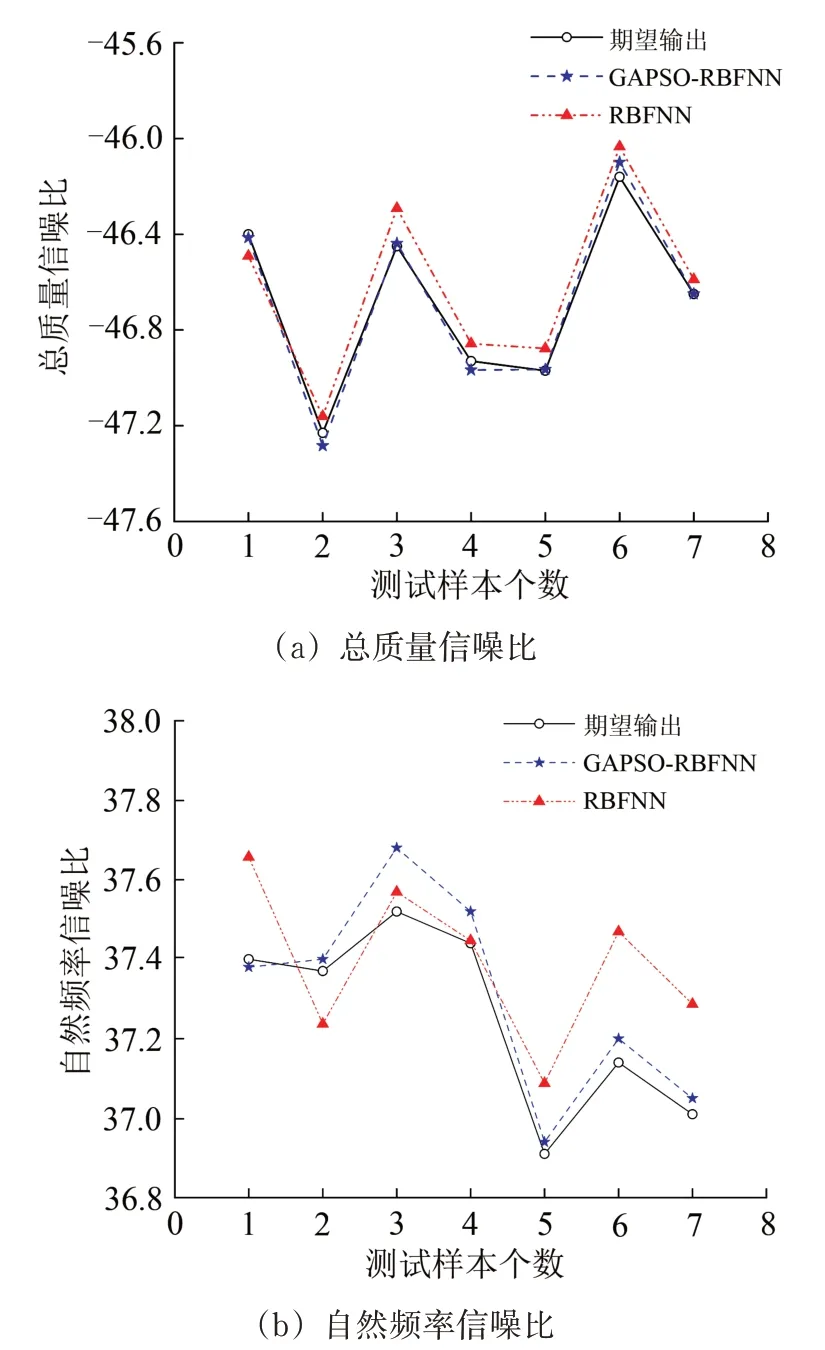
图4 GAPSO-RBFNN与RBFNN预测结果对比

对于机械系统而言,当外界激励频率与自然频率相等时,系统将发生共振。而实际工程中,理想的共振情况很难发生,一般取fr∈(0.95ϖn,1.05ϖn)作为共振准则,其中ϖn为激励频率的均值［22］,fr为电机吊架的自然频率。为避免电机吊架与牵引电机发生共振,电机吊架的自然频率应高于牵引电机工作频率的上限点73.53 Hz。以GAPSO-RBFNN的各质量特性信噪比输出最大为优化目标,并给出相应的约束条件构建电机吊架多目标稳健优化模型可表述为

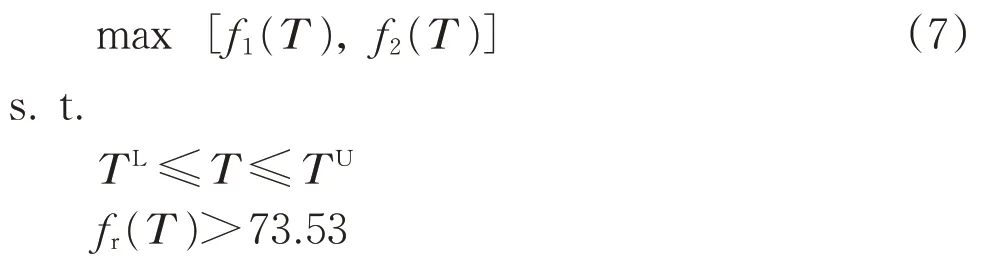
式中：f1(T),f2(T)分别为GAPSO-RBFNN总质量信噪比和自然频率信噪比输出；T为设计变量,T={T2,T4,T6,T7,T9,T10}；TU,TL分别为设计变量T的上、下界。

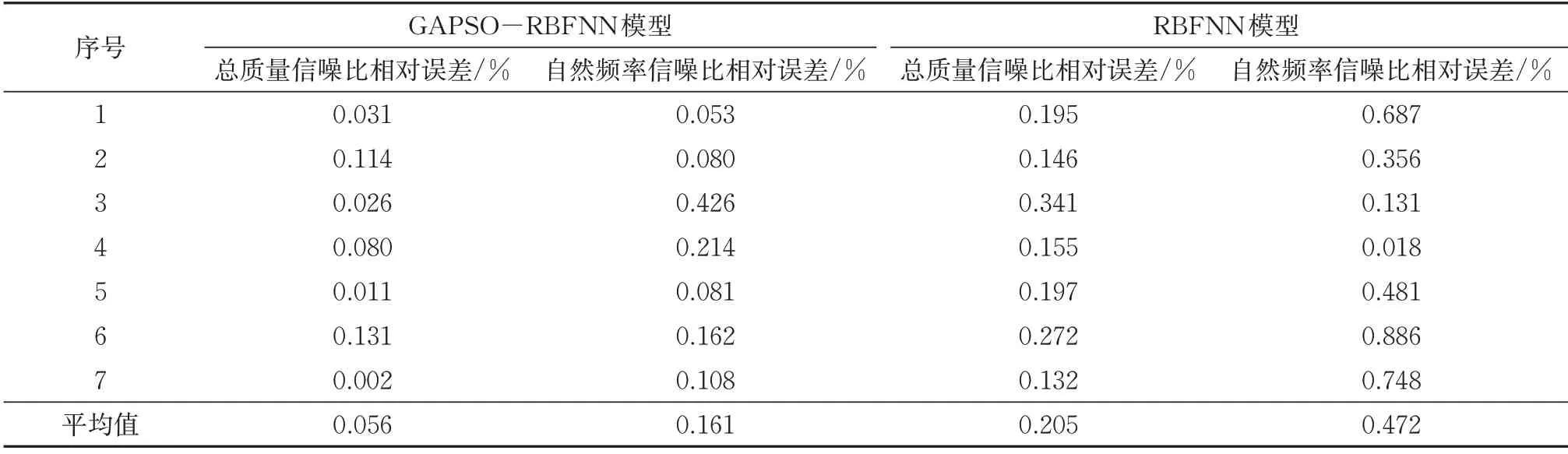
表5 GAPSO-RBFNN 和RBFNN预测结果相对误差

3.3 模型求解及结果分析

选择具有较高计算性能的第二代非支配遗传算法（NSGA-II）［23］求解建立的电机吊架多目标稳健优化模型。

将训练好的GAPSO-RBFNN 的输出作为NSGA-II的适应度值,展开对电机吊架总质量信噪比和自然频率信噪比的极大值寻优。设置NSGA-II的交叉概率为0.9,选取种群规模为200个,Pareto前沿解的数量为50 个,最大迭代次数250 次,对电机吊架的多目标稳健优化模型求解得到的Pareto前沿如图5所示。

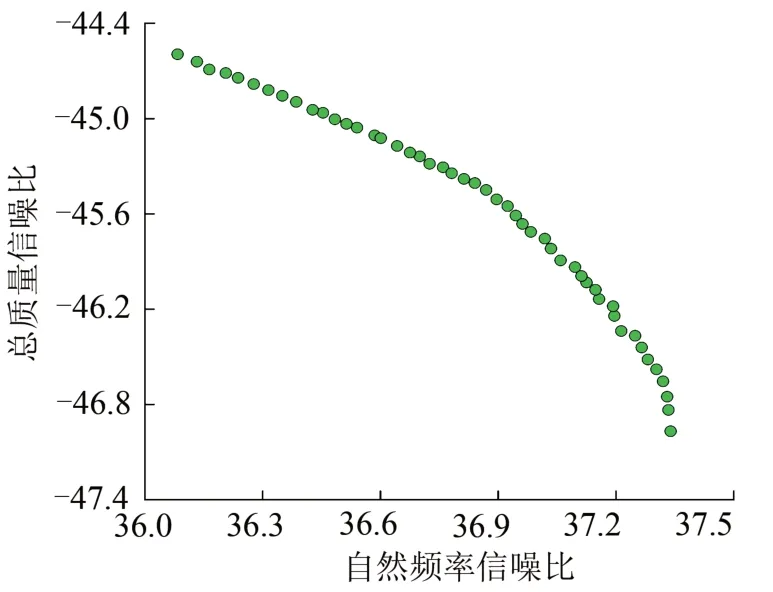
图5 NSGA-II算法优化结果

考虑Pareto最优解集选优过程受到的主观因素影响,选用模糊集合理论［24］对Pareto 最优解集进行选优。根据模糊集合理论计算出Pareto解集中每个解的支配度。支配度越高,意味着该解的性能越好。因此,选择支配度最高的解作为Pareto解集的最优解。Pareto 解集中解的支配度分布图如图6所示。从图6可以看出,第36号解的支配度最高。因此,选择36 号解作为最优解,进而得到电机吊架多目标稳健优化设计方案。

将得到的多目标稳健优化设计方案与传统设计方案进行对比分析,分析结果见表6。由表6可以看出,优化后的电机吊架总质量和自然频率的信噪比分别提高了2.59%和1.90%,降低了不可控因素对电机吊架总质量和自然频率的干扰,有效地提升了电机吊架各质量特性的稳健性。在满足电机吊架稳健性提升的同时,电机吊架质量降低了1.30%,自然频率提高了6.04%。

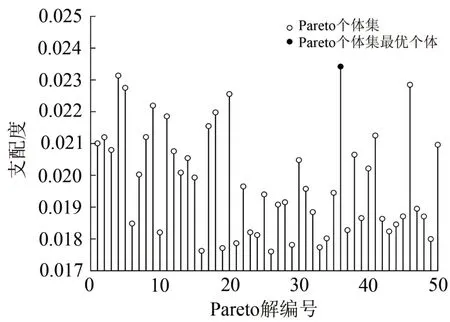
图6 Pareto解集支配度分布图

表6 传统设计方案与稳健优化方案对比

4 结 论

（1）基于GAPSO 算法优化RBFNN 平滑系数,建立改进的RBFNN 即GAPSO-RBFNN,并且将其预测精度与传统RBFNN 进行对比,结果显示GAPSO-RBFNN的预测精度明显提高。

（2）采用信噪比作为衡量电机吊架各质量特性的稳健性指标,以GAPSO-RBFNN 对电机吊架总质量和自然频率信噪比的预测输出最大化为优化目标,构建了电机吊架的多目标稳健优化模型,并采用NSGA-II 算法对其求解。优化结果表明电机吊架各质量特性信噪比得到提高,降低了不可控因素对电机吊架总质量和自然频率的干扰,进而实现了电机吊架各质量特性的稳健性。

（3）对电机吊架的稳健优化实例表明,本文所提方法不仅实现了电机吊架的稳健优化设计,还降低了电机吊架总质量,提高了其自然频率,满足动车组设计轻量化要求,具有一定的工程实用价值,同时为其它轨道车辆关键部件的稳健优化设计提供了可行性途径。