基于磁热力耦合的高压大截面电缆热机械效应研究
付明星,王善红,潘 恒,王 坤,马宏忠
(1.国网江苏省电力有限公司盐城供电分公司,江苏 盐城 224002;2.河海大学 能源与电气学院,江苏 南京 211100)
0 引言
高压电缆作为电能传输的重要载体,在城市输配电系统中已被广泛应用,提高电力电缆运行可靠性对确保城市生产生活有重要意义[1-2]。因城市电网升级改造及不同客户发展需要,大截面电力电缆需求量也日益倍增。与电网中其他电气设备相似,电力电缆在长期运行过程中,受外界环境和电力工况变化的影响,也会出现一些潜伏性故障[3-4]。
电缆内部因负荷电流变化引起导体温度变化导致电缆热胀冷缩,由此产生的膨胀力或收缩力统称为热机械力。热机械力导致电缆产生的变形、位移等现象统称为热机械效应。过大的热机械力会破坏电缆本体、接头、终端结构,导致电缆起拱、位移、过分弯曲进而损坏电缆。此外,在热机械力的作用下电缆反复出现弯曲变形会引起金属护层产生疲劳应变。经相关电力部门统计,江苏地区近几年的高压电缆故障案例中,因热机械力诱发的故障比例高达36.2%,但由于目前国内外针对热机械力开展的研究甚少,在进行高压电缆故障分析时容易忽略电缆运行热机械力的影响,未能及时处理电缆运行的潜伏性故障[5]。因此,开展大截面电缆热机械效应的建模研究,可有效评估电缆运行状态,及时发现电缆异常运行状态。
现有关于电缆热膨胀方面的研究大多关注电缆温度场的建模计算研究,George J.Anders 等以浅槽敷设的电缆为研究对象,考虑槽内空气热阻特性,建立电缆载流量计算模型[6]。Millar R J 等将电缆导体温度表达式描述为多阶指数函数的和,在电缆温升实验数据的基础上,借助指数拟合方法确定电缆导体温度表达式参数[7]。杨永明等通过耦合空气流场建立电缆有限元模型,定量分析空气散热对电缆温度场的影响[8]。王健等建立GIL 的热力耦合模型,分析GIL 热致伸缩和机械振动特性[9]。虽有文献已开展高压大截面电缆的热膨胀计算,但计算采用经验公式,并未开展高压大截面电缆的热机械效应建模研究[10-11]。
以220 kV 高压大截面电缆为研究对象,采用有限元法,建立高压大截面电缆热应力与热应变的磁热力耦合计算模型。通过仿真计算得到不同负荷电流下电缆热应力及热应变的数值大小及其分布特点,借助数据拟合方法获取电缆导体及金属护层热应力与负荷电流的关系式。
1 电缆磁热力耦合场的数学模型
高压电缆的运行过程实质上是电缆电磁场、温度场以及应力场相互作用的过程,计算电缆热应力和热应变需要进行电缆多物理场耦合计算。以空气敷设下电缆三维模型为研究对象,依次给出电缆的电磁场、温度场及应力场的数学模型。
1.1 电磁场数学模型
电缆各层的矢量磁位控制方程可表示为[12-14]

式中:A 为对应区域的矢量磁位;μ 为材料的磁导率;Jc为电流密度,对于有源区域,如导体、金属护层,Jc不为0,对于非有源区域,如绝缘、外护套等,Jc直接取0。
1.2 温度场数学模型
为计算电缆热应力和热应变,须建立电缆的三维模型,电缆三维温度场的数学模型可描述为[15-16]
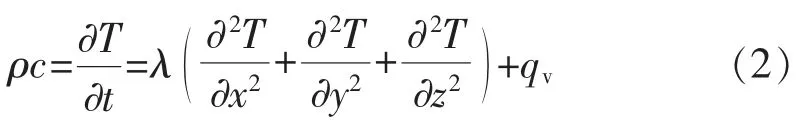
式中:ρ 为材料密度,kg/m3;c为材料的比热容,J/(kg·K);T 为计算区域内任一点(x,y,z)处的温度,K;λ 为材料的导热系数,W/(m·K);qv为单位体积产热率,W/m3。对于含热源区域,如导体、金属护层,qv不为0;而对于不含热源区域,如缓冲层、外护套,qv取0。
1.3 应力场数学模型
电缆因温度变化会在内部产生热应力,其数学表达式可描述为[17]
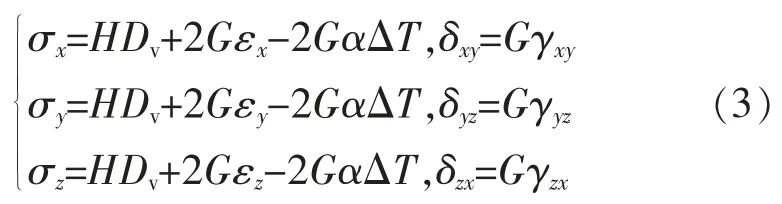
式中:σx、σy、σz分别为x、y、z 轴方向的应力分量;δxy、δyz、δzx分别为xy、yz、zx 平面的应力分量;H、G 为拉梅常数;α 为热膨胀系数;ΔT 为温度差;εx、εy、εz分别为x、y、z 轴方向的应力分量;γxy、γyz、γzx为xy、yz、zx 平面的应变分量;Dv为体积应变,Dv=εx+εy+εz。
通过几何方程描述应变分量为
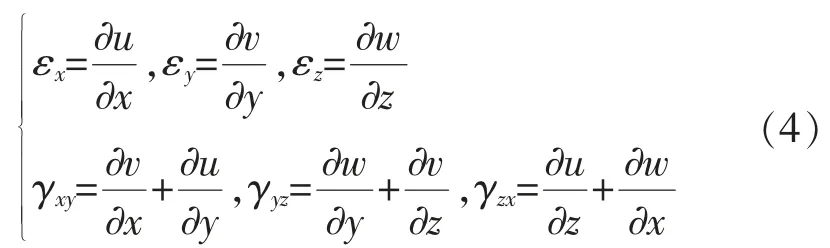
式中:u、v、w 分别为位移沿x、y、z 轴3 个方向的投影分量。
应力平衡方程可以表示为[18]
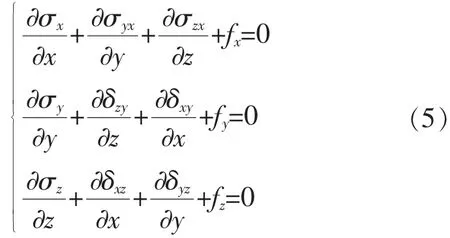
式中:fx、fy、fz分别为电缆所受力沿x、y、z 轴3 个方向的投影分量。
最终得到用位移分量表示的应力场控制方程为
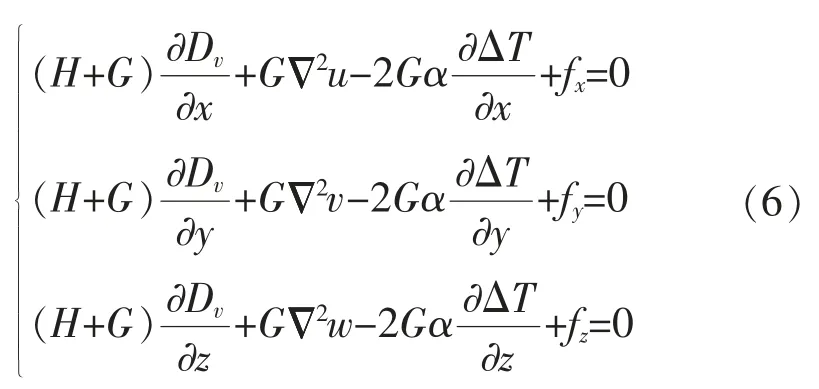
式中:若电缆沿x 方向固定,则可对应取u 为0,其他方向类推。
2 高压大截面电缆有限元模型
2.1 电缆物理模型
高压大截面电缆是指电压等级在220 kV 及以上、截面积大于1 000 mm2的电力电缆。以两个抱箍固定的220 kV 大截面电缆(型号为YJLW03-Z-127/220 kV-2 500 mm2)为建模对象,建立大截面电缆的磁热力耦合三维模型以计算运行电缆的热应力和热应变大小。表1 为220 kV 电缆结构参数,建模时取电缆长度为3 m,以电缆径向为x 轴、电缆轴向为z 轴,电缆物理模型的径向与轴向如图1 所示。

表1 220 kV 电缆结构参数 mm
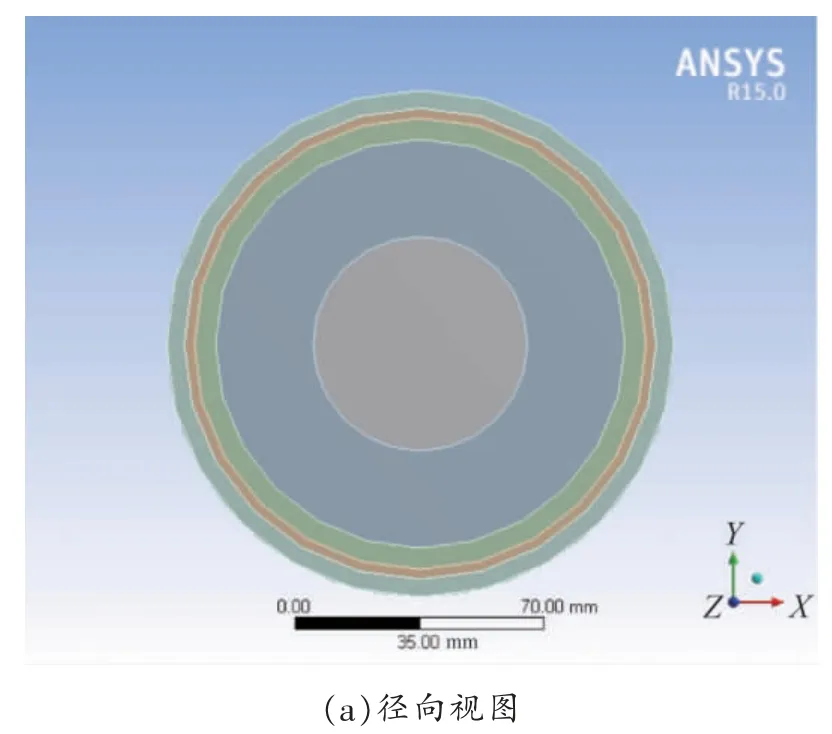
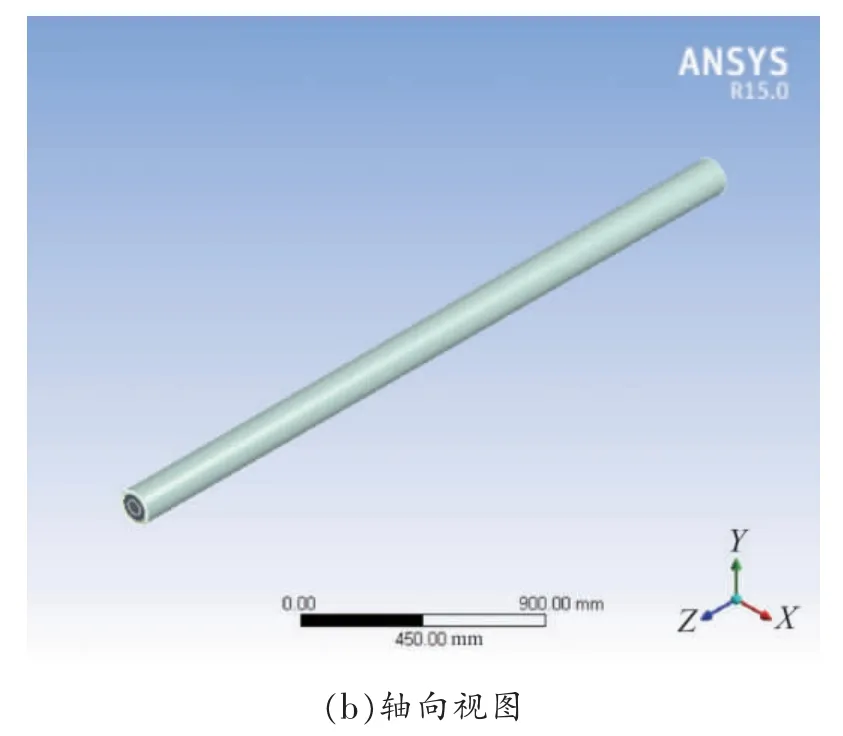
图1 电缆物理模型
2.2 边界条件
考虑到矢量磁位在电缆外部空气域中会迅速衰减的特性,将空气域封闭在距离电缆本体1 000 mm处,将电缆径向设置为x 轴和y 轴,将电缆轴向设置为z 轴,具体求解域模型如图2 所示。
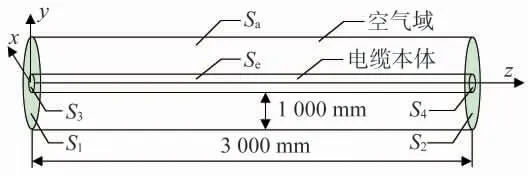
图2 电缆耦合场求解域模型
根据图2,将边界条件具体设置说明如下。
1)电磁场边界条件。
在距离电缆本体1 000 mm 空气域处,矢量磁位已迅速衰减为0,因此求解域的外边界条件可描述为

电缆轴向两端径向截面为磁绝缘边界条件,数学描述为

式中:n 为边界法向量。
2)温度场边界条件。
空气敷设下电缆主要通过对流换热和辐射换热2 种方式向外界传递热量,对流换热边界可以描述为
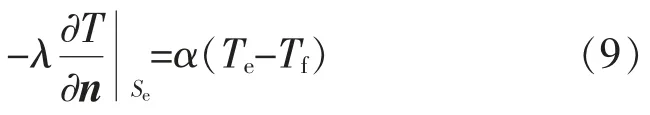
式中:α 为电缆外表面对流换热系数,取5.6 W/(m2·K);Te为电缆外表面温度,℃;Tf为环境温度,℃。
电缆表面的辐射换热边界数学描述为
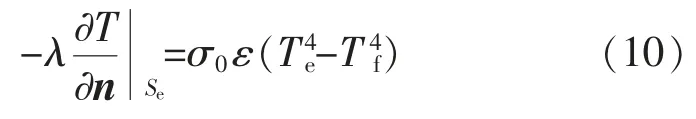
式中:σ0为Stefan-Boltzmann 常数,其值一般取5.67×10-8W/(m2·K4);ε 为表面发射率,取0.6。
考虑到电缆轴向温度变化小到基本可以忽略,电缆两端径向截面的法向温度梯度为0,数学描述为

3)应力场边界条件。
以两端抱箍间电缆为建模对象,抱箍的预紧力使电缆两端面的轴向位移分量几乎为0,因此认为电缆本体在S3、S4截面上的位移是沿径向的,数学描述为

式中:l 为电缆位移分量。而电缆外表面Se则不存在外力和位移条件约束,即满足自由边界条件。
3 仿真结果分析
利用ANSYS 软件建立电缆模型。当电缆线芯导体通入2 280 A 电流时,电缆各层电磁损耗的径向截面分布如图3 所示。
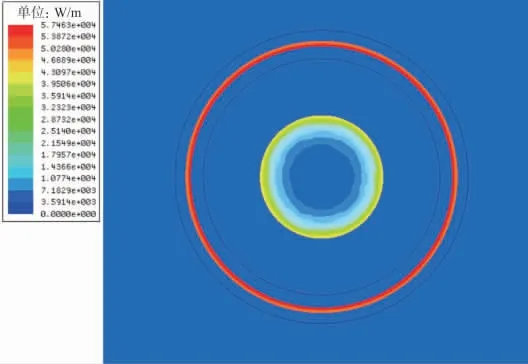
图3 电缆电磁损耗的径向截面分布
将电缆电磁损耗计算结果作为热载荷耦合到电缆温度场模型中,得到电缆各层温度场的径向截面和轴向剖面分布如图4 所示。从图4 的温度云图可知,当导体电流为2 280 A 时,此时电缆导体温度为89.96 ℃,三维电缆各层温度主要沿径向变化,电缆轴向各处温度基本无变化,即电缆轴向温度梯度基本为零。
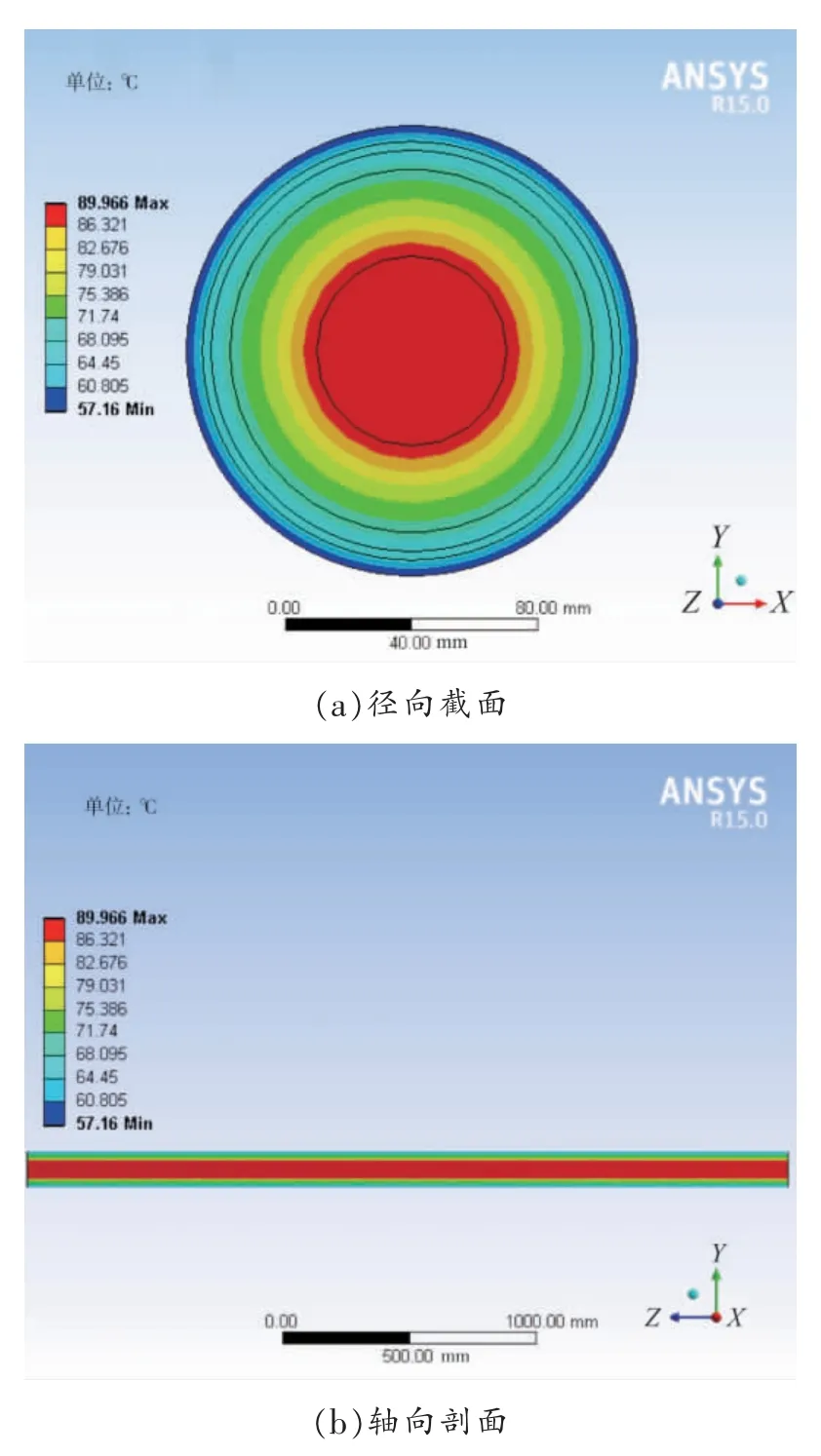
图4 电缆各层的温度场分布
同理,将上述的电缆温度场计算结果作为温度载荷耦合到电缆应力场计算模型中,可得电缆各层热应力和热应变的径向和轴向分布如图5 和图6 所示。
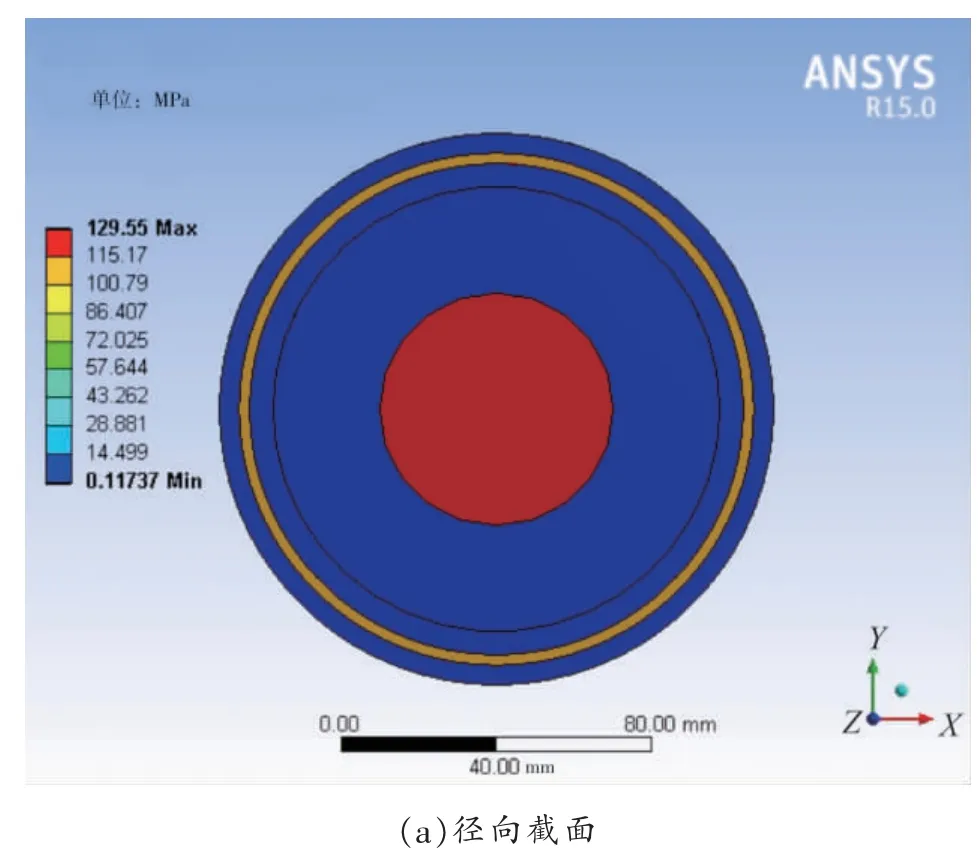
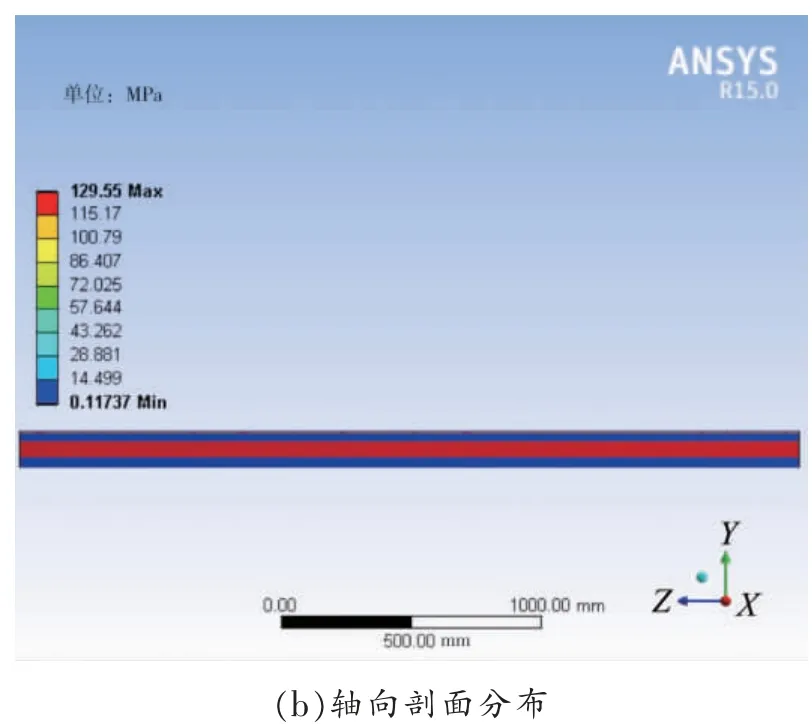
图5 电缆各层的热应力
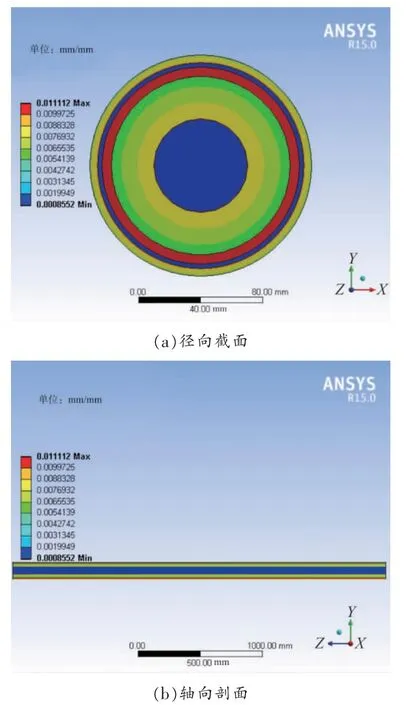
图6 电缆各层的热应变分布
由于电缆轴向温度梯度基本为零,电缆热量沿径向传递,因此电缆各层的热应力和热应变沿轴向基本没有变化,主要沿径向呈现不同大小。从图5(a)可知,运行电缆热应力较大值主要出现在电缆线芯导体和金属护层中,电缆其他各层热应力值比较小。当电缆线芯导体温度达到89.96 ℃时,电缆导体处的热应力大小为129.55 MPa,其金属护层处的热应力为111.48 MPa,其他各层的热应力大小在2 MPa 以内。从图6(a)可知,运行电缆热应变较小值出现在电缆导体和金属护层中,这是因为电缆导体和金属护层所用的金属材料热膨胀系数比其他各层材料的膨胀系数小。
通过改变输入电缆导体的电流值大小,可得不同负荷电流下,电缆各层热应力和热应变分布曲线,如图7 和图8 所示。
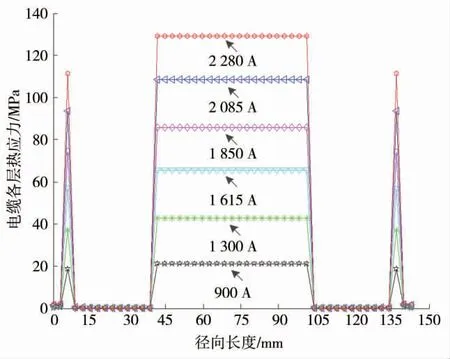
图7 不同负荷电流下电缆各层热应力
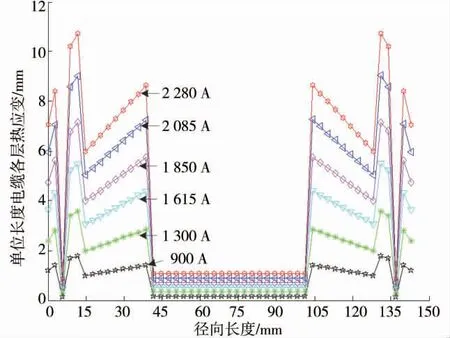
图8 不同负荷电流下电缆各层热应变
根据不同负荷电流下电缆导体和金属护层热应力仿真计算数据,可得导体和金属护层热应力与负荷电流之间关系曲线如图9 所示。借助数据拟合方法,导体及金属护层热应力和负荷电流之间关系见式(13)和式(14)。
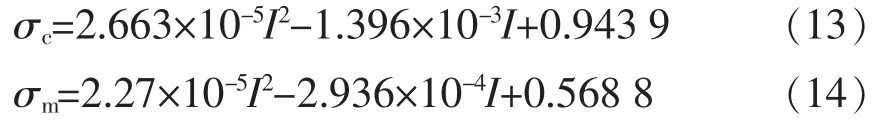
式中:σc为电缆线芯导体热应力,MPa;σm为电缆金属护层热应力,MPa;I 为运行电缆负荷电流,A。
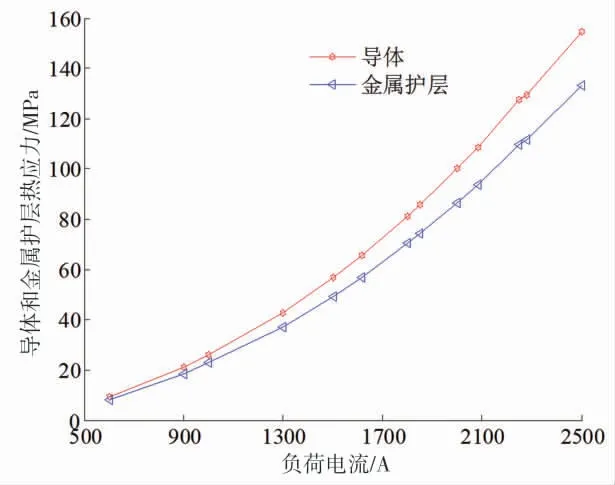
图9 电缆导体及金属护层与负荷电流的关系曲线
4 结语
建立高压大截面电缆的磁热力耦合计算模型,以电缆各层的电磁损耗为载荷,获得电缆各层的温度和力学特性分布结果,分析电缆热机械效应特点。根据仿真结果可得以下结论:
1)高压大截面电缆温度场主要沿径向分布,轴向温度梯度近似为零。
2)运行高压大截面电缆的热应力主要集中分布在导体与金属护层,但其热应变很小。
3)电缆导体与金属护层的热应力和负荷电流成二次函数关系,采用数据拟合方法确定关系表达式,可为电缆运行状态监测提供参考。
4)当高压电缆长期处于重载状态(导体温度在70 ℃及以上),其内部热应力与热应变大小不可忽略,在敷设电缆时按一定距离设置伸缩弧可缓解电缆内部热机械损伤。

