学情明了本源清 四度抽象得归真

【研究缘起】

新学期将始，打开浙教版新思维小学《数学》课本，第一课就是“生活中的比”。不由得想起三年多前在张奠宙先生家里为撰写《小学数学教材中的大道理——核心概念的理解与呈现》一书中的“数方夜谈”而与先生促膝长谈的情景，于是又翻出先生《返璞归真 正本清源——“比”不能等同于除法》一文细细研读，反复参详先生的基本观点。

（一）“比”是一种数量关系。“比”不是除法运算，只是在求比值时才要用除法。（二）“比”是为比例做准备，并可以扩展为一种变量之间的正比例函数关系。这种比例关系，其含义远超“除法”。（三）“比”原本是同类量的比较关系，但是也可以推广到不是“同类量”的情形。不过，同类量之比是“源”，不同类量之比只是“流”。（四）不同类量的比，不宜作为“比”的主要情境引入。（五）同类量的比值没有量纲，不同类量的比值一定会有量纲。（六）把“两个数相除，又叫作两个数的比”作为“比”的定义，乃是舍本逐末。

我们做了课前调查，调查题目是：在现实生活中，你在哪里见到过（或听到过）“比”？写出这些“比”。结果表明：有42%的学生知道配方中的比;有90%以上的学生提及球赛中的比分;没有人提及不同类量的比。

【研究内容】

聚焦下面四个问题做进一步的研究。

其一，如先生所言，“两个数相除，又叫作两个数的比”不能体现比的意义的本质，学生难以从中体会学习的意义和价值。那么，我们能不能用含义远超“除法”的“比例关系”来引入“比的意义”，确立“比”作为数学核心概念的地位？如能，必将更有利于学生体会学习“比”的必要性。已有的研究是这样从比例关系的角度定义比的意义的：两个相依变化的量X、Y，当X取值为a时，Y有唯一确定的值b与之对应，当X取ka时，Y有唯一确定的值kb与之对应，我们把X、Y之间的这种关系称为比，用a∶b表示，读作a比b。这显然是一个函数化了的定义，蕴含了比的基本性质。关于这一定义的可接受性，下文将给出实践验证。

其二，同类量之比是“源”，不同类量之比只是“流”。如何利用“42%的学生知道配方中的比”这一学习资源教学同类量之比？“没有人提及不同类量的比”，这给我们提出了一个问题，即如何自然地把源于两个“同类量”的比推广到“不同类量”的情形，使教学能免于机械的“告知—接受”模式。

其三，比可以表示成分数的形式，其合理性何在？这涉及如何引导学生深刻理解比与分数的关系的问题。既然“只是在求比值时才要用除法”，是否可以由求比值的需求，引出比与除法的关系？这涉及如何引导学生准确理解比与除法的关系的问题。

其四，“90%以上的学生提及球赛中的比分”，如何处理“比分”问题？教学时，教师通常会让学生辨析下列哪个是今天所研究的比：“甲乙两支足球队的比分是3∶2”“男女生的人数比是3∶2”。学生通常认为前者是“差比”，不是今天研究的比，后者是“倍比”，是今天研究的比。前者就不能是“倍比”？当然能：甲队进球数是乙队的[32]倍，乙队进球数是甲队的[23]。如何作出合理的解释？

【研究实践】

下面结合教学实践来具体谈谈这些问题。教学分为两课时：第一课时教学同类量之比——“源”，建立比与分数的联系;第二课时引入不同类量之比——“流”，定义比值，建立比与除法的联系。

第一课时

1.感悟共变规律，探索配方表示

（1）创设问题情境，激发主动探究

王师傅用一种浓缩果汁和水配制饮料，他配了三份饮料：

第一份用了200mL果汁和800mL水;

第二份用了400mL果汁和1600mL水;

第三份用了300mL果汁和1200mL水。

想一想：王师傅三次配的饮料味道一样吗？ 你能用不同的方法来说明吗？

（2）探索变中不变，初识比的意义

生：第二份饮料中果汁的量是第一份饮料中果汁量的2倍，水也是2倍，这就相当于把第一份飲料同样的配2份，然后倒在一起，所以两份味道一样;第三份饮料中果汁和水的量都是第一份的1.5倍，味道也一样。

生：每一份饮料中果汁的量都是水量的[14]，水量是果汁量的4倍，它们的配制方法是一样的，所以味道一样。

生：每一份饮料中都是果汁1份，水4份，果汁与水的比是1∶4，水与果汁的比是4∶1，三次的配方是一样的，所以味道也一样。

小结：这就是我们今天学的新知识——比，有了比，我们可以把“几倍”和“几分之几”统一成一种说法——比。

（3）经历量性抽象，引入字母代数

教师提问：你还能配出味道相同的饮料吗？学生进一步举例。如：果汁150mL，水600mL，等等。教师继续提问：能不能举一个例子包括所有可能的情形？学生答：果汁是kmL，水是4kmL。

小结：果汁和水的数量在变化，但它们之间的关系保持不变。它们的关系可以用比来表示——果汁与水的比是1∶4，水与果汁的比是4∶1，表示果汁是1份，水是4份，若果汁的量为k，那么水的量就是4k， k是每份数。

（解析：充分利用学生已有的关于配方及其表示的知识经验，用三份饮料口味是否相同的问题引发思考，体会蕴含其中不变的比例关系，引入用比表示配方的方法，通过举例和量性抽象，为后续进一步学习数学抽象做好铺垫。把“几倍”和“几分之几”统一成一种说法——比，为今后研究和表达“比”的这种关系带来很大便利。）

2.丰富关系例证，积累活动经验

（1）独立学习

请学生填表，并说说表中什么在变，什么不变。想一想：如何表示表中两个相依变化的量之间的关系？

①某商品成本与利润关系如下：

[成本/元 10 100 150 600 利润/元 3 30 45 60 3m ]

成本与利润之间的关系是：

②某一时刻测得树高与影长的关系如下：

[树高/米 50 15 1.5 影长/米 30 9 3 0.3 ]

树高与影长之间的关系是：

（2）合作交流，校对讲评（过程略）

3.经历逐级抽象，形成概念表征

（1）经历质性抽象，形成变量表征

用X、Y分别表示果汁和水：

[X 200 400 300 150 1 k Y 800 1600 1200 600 4 4k ]

两个相依变化的量X与Y的比是1∶4，Y与X的比是4∶1。

同样，我们也可以用X、Y分别表示成本和利润、树高和影长：

[X 10 100 150 200 600 10m Y 3 30 45 60 180 3m ]

两个相依变化的量X与Y的比是10∶3， Y与X的比是3∶10。

[X 50 15 5 0.5 1.5 5n Y 30 9 3 0.3 0.9 3n ]

两个相依变化的量X与Y的比是5∶3， Y与X的比是3∶5。

（2）再次量性抽象，形成概念表征

我们可以用a、b来表示上述各比中的具体数，得到：两个相依变化的量X与Y的比是a∶b， Y与X的比是b∶a。

师生讨论且填写下表（开始呈现时仅出示第一列）。

[X a 2a 50a [a2] [35a] ak Y b 2b 50b [b2] [35b] bk ]

想一想：表中最重要的是哪几列？学生认为是第2列和最后一列。想一想：能否据此来说一说什么叫作比？

呈现定义：两个相依变化的量X、Y，当X取值为a时，Y有唯一确定的值b与之对应，当X取ka时，Y有唯一確定的值kb与之对应，我们把X、Y之间的这种关系称为比，用a∶b表示，读作a比b。

在上面的三个例子中，两个相依变化量的单位相同，称为同类量。同类量X、Y的比是a∶b，表示X有a份，Y有b份，k是每份数。

（解析：质性抽象舍弃了具体的问题情境，从一般意义上给出了两个同类量X和Y，经过第二次量性抽象，给出了关系的一般表示a∶b或b∶a，这样，就从一般意义上定义了同类量的比。抽象是数学最本质的特征，正是因为抽象，才使源于同类量的“比”推广到不同类量的情形有了逻辑的可能性。）

4.体会取值范围，展开反例辨析

（1）任选一题，用多种方法解释比的意义

①新生儿头长与身高的比是1∶4。

[头长/cm 身高/cm ]

②汽车匀速行驶2小时与5小时的路程比是2∶5。

[行2小时路程/km 行5小时路程/km ]

交流时提醒学生注意取值范围，如新生儿头长不能取1cm、1m，汽车行驶速度则不能取1000km/h，等等。

（2）下面的信息中有比吗？如果有，请你写出来

①许多小区配置的车位数和住户数一样多。

②国旗法规定国旗的宽是长的[23]。

③每1000kg的海水中所含盐的质量是35kg。

④足球比赛上半场甲队进2球，乙队进1球。

题目①②③的比分别是车位数与住户数的比是1∶1，国旗宽与长的比是2∶3，海水与盐的比是1000∶35。教师着重辨析第④题：上半场甲乙两队的比分是2∶1，根据比的意义，2∶1与6∶3表示的关系是一样的，只是每份数取了不同的值而已，但在球赛中，上半场甲乙两队的比分2∶1与6∶3是完全不一样的概念，绝不能等同视之，所以这一题中不存在我们今天研究的比。

（解析：对应关系和定义域是函数概念中的两个关键要素。第一题的两个例子渗透了定义域的思想，有利于培养学生的应用意识。用“差比”来解释球赛“比分”中的比不是今天所研究的比，难免有点牵强附会，使用新的定义对此作出了较为令人满意的解释——本质上是因为它不适用比的基本性质。）

5.关联比与分数，拓展比的表示

（1）引入分数表示，关联比与分数

介绍比的前项、后项和比号。呈现：比也可以用分数的形式表示，如1∶4也可以写作[14]。想一想：为什么比可以用分数形式表示？

学生解释：1∶4表示两个量是1份和4份的关系，它们包含的每份数相同，根据分数的意义，分数[14]也是每份数相同的1份和4份，两者并不矛盾。

（2）拓展比的表示，深化份数理解

用比表示下列各题中数量之间的关系。

①搅拌混凝土，需要沙子30kg，石子50kg，水泥20kg。

②

（解析：同类量的比，从一开始的引入，就是与分数、倍数表示等价的，但更为便捷的一种方法，引入比的分数表示，也是顺理成章的，有利于学生从同类量之比、分数的意义上更深刻地理解两者的联系——形式上的通用是源于意义上的共通，养成缜密的思维习惯。）

第二课时

1.再现意义抽象，夯实推广基础

呈现上节课同类量比的三个例子，快速再现质性抽象和量性抽象的过程，复习同类量比的意义。

2.再次质性抽象，实现引源入流

独立学习：填表，并说说什么在变，什么不变。想一想：如何表示表中两个相依变化的量之间的关系？

汽车匀速行驶的路程与时间的关系如下：

[路程/km 80 120 160 320 时间/h 1 1.5 2 3 m ]

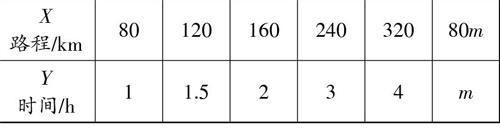
教师提问：这张表与上节课的表像吗？学生认为很像，不同的是上节课是两个同类量，这节课是不同类量，但我们也可以用X、Y分别表示路程和时间：

[X

路程/km 80 120 160 240 320 80m Y

时间/h 1 1.5 2 3 4 m ]

这就得到了与上节课完全一样的表格，既然抽象后的形式相同，上节课用于表示两个相依变化量X、Y之间关系的“比”也应当适用于当下的情形：

两个相依变化的量X与Y的比是80∶1， Y与X的比是1∶80。

回到原问题中：路程与时间的比是80∶1，时间与路程的比是1∶80。

小结：比也适用不同类量的情形。

（解析：引源入流的关键一步是数学抽象，经过抽象，我们发现，路程和时间这两个不同类量之间的关系具有和两个同类量之比完全相同的形式，这就说明两者本质上是一样的，都是比例关系。因此，适用于表示同类量之间关系的比自然也应该适用于不同类量的情形，这样的推广合情合理、水到渠成。）

3.概括同质例证，丰富抽象基底

（1）某种商品总价与数量之间关系如下：

[总价/元 15 25 30 5 数量/件 3 5 6 8 a ]

总价与数量之间的关系是：

（2）工程队工作总量与工作时间之间的关系如下：

[工作总量/件 24 120 工作时间/天 12 ]

工作总量与工作时间之间的关系是：

小结：我们同样可以用X、Y分别表示路程与时间、总价与数量、工作总量与工作时间，用a、b来表示上述各比中的具体数。这样，今天研究的不同类量之间的关系和上节课的同类量之间的关系具有完全相同的形式，上节课所学的比也同样适用于表示两个不同类量之间的关系。

4.适时引入比值，关联比与除法

果汁与水的比是1∶4，这是果汁与水在比，我们把“果汁是水的[14]”看作比的结果，把[14]叫作1∶4的比值，记作1∶4=[14]，这是两个同类量之间的倍比关系，比值不带单位。

路程与时间的比是80∶1，这是路程与时间在比，比的结果是什么呢？学生认为是速度，80∶1=80（km/h），这是两个不同类量的比，比值帶有单位。

观察比与比值的关系，你还想到了什么？学生发现：后者即是路程÷时间=速度;前者是求一个数是另一个数的几分之几，用一个数除以另一个数。

小结：鉴于比与除法的关系，在数学里，两个数相除通常也可以写成两个数的比，两个数的比通常也可以写成两个数相除。可以用比的前项除以后项的方法来求比值。根据比与除法的关系，我们也可以用分数形式表示80∶1为[801]。

（解析：这一环节先引出两个量相比的结果叫比值，然后引导学生发现比值其实就是这两个量相除的商，进而建立起比与除法的关系。这样的教学，比不再是换个说法的“又叫”，“求比值才要用除法”，凸显了比自身的独立价值，置除法于从属地位。）

5.探索相似性质，引入等比概念（略）

相比于“两个数相除又叫两个数的比”，新的定义凸显“比”作为数学核心概念的应有风貌：从定义的比例背景可以自然地引出比的基本性质，即a∶b=ak∶bk。方便地验证比例的基本性质，即a·bk=b·ak。作为同类量之比的应用，按比例分配、比例尺中的“比例”两字真正获得了比例的意义，其中的比表示变量之间不变的关系，当一个变量取某一特定的值时，其他的变量就取对应的确定值。正反比例的定义关注了不变量，即正比例的比值一定、反比例的积一定，而正反比例的性质关注了变的规律，所谓的正比例性质是指：成正比例关系的两个量，一个变量的两个取值之比与另一变量的两个相应取值之比相同，称一个比是另一个比的正比。反比例性质是指：成反比例关系的两个量，一个变量的两个取值之比与另一变量的两个相应取值之比相反，称其中一个比是另一个比的反比。比的概念衔接了正比例的定义和性质，也能方便地用于反比例问题（反比例即变量X的取值与变量Y的取值的倒数成正比）。正反比例的性质凸显了正反比例关系的应用价值，如物理学的许多定律表述都与正反比例性质有关，如欧姆定律：I=U/R，导体中的电流跟导体两端电压呈正比，跟导体的电阻呈反比。不仅如此，从教学的实际来看，学生在解决应用问题时并不喜欢课本、教师要求他们的根据定义列方程解的方法，用正比、反比解题反而更受欢迎。

（谨以此文纪念张奠宙先生）

参考文献：

[1]张奠宙.返璞归真正本清源——“比”不能等同于除法[J].教学月刊·小学版（数学），2015（3）.

[2]任敏龙.从两个数相除到生活中的比[J].教学月刊·小学版（数学），2016（11）.

（浙江省杭州市上城区教育学院   310002）