连梁桩基础桩顶位移计算分析

陈 顺 郭艳军 王泽毅

（四川电力设计咨询有限责任公司 四川成都 610041）

0 引言

随着目前输电线路电压等级的提高，铁塔的基础作用力越来越大，基础水平力也是越来越大。对于桩基础，不仅要计算桩基础的抗压和抗拔，还需要计算桩顶的水平位移。对于桩基础一般采用弹性地基梁M法计算水平荷载作用下的内力与位移，大多数行业规范[1-2]都推荐采用这种方法。桩在水平荷载作用下，桩身产生变形，这种变形受到周边岩土的约束。弹性地基梁M法基本假定：①将桩侧土视为弹性介质；②不考虑桩身与桩侧土体的摩擦力与粘结力；③在土层任一深度处所产生的水平抗力与该点水平位移xz成正比，即σ=cxz且地基系数c随深度增加成正比增长，即c=mz。基于这些基本假定，进行桩的内力与位移的理论公式推导和计算。桩顶有Q水平荷载及弯矩M作用，此时桩身会发生弹性挠曲，对桩测土体产生作用，桩侧土体将产生横向抗力σxz由弹性力学可知，梁轴的挠度与梁上分布荷载q之间的关系式，即梁的挠曲微分方程为：

式中：E，I-桩惯性矩，对于桩即为桩的弹性模量和惯性矩。单元内桩侧土产生的抗力q=σxz·b0。桩基础挠曲方程为：

式中：E、I-桩的弹性模量和惯性矩；σxz-桩侧土抗力；b0-桩基础的计算宽度，xz为桩基础在深度Z处的水平位移。

将上式变形可得：

式中：α-桩的水平变形系数。式（4）是一个四阶线性变系数齐次微分方程，可以利用幂级数展开求解该微分方程[3]，计算桩的水平位移xz。

求解该方程可以计算桩的位移和内力，手册将上述公式计算结果做成表格，工程技术人员查表使用。

在实际工程中，土体通常会有多层土层组成，桩基规范[4]建议将多层土的桩侧土水平抗力系数换算成理想均质土层时的水平抗力系数，通过求解在均质土层的内力和位移，得到桩基础在多层分层土中的内力和位移。当桩侧土体有2种土层时，

若桩周有3种土时：

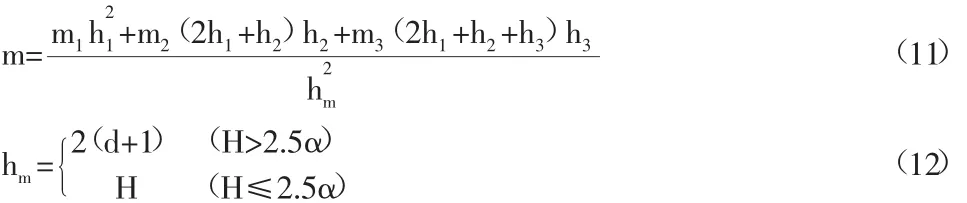
式中：α-桩的变形系数。

根据赵明华[5]的研究，采用现行规范建议的桩侧土水平抗力系数换算法，计算得到的桩身内力和位移与试验中的桩身内力和位移有较大差异，通常这种差异会导致桩基础设计的不安全。提出了一种通过加权叠加桩身的变形绕曲线，然后换算侧土水平抗力系数的方法，这种方法使得求解桩基础的内力和位移计算精度大大提高。但是，无论采用规范法还是加权桩身绕曲线换算法，都需通过传统的M法换算计算深度，然后采用查表计算的方式，计算桩身在不同深度处的内力和位移，这种计算方法通常都较为繁琐且受人为影响较大。为了反映实际土体的在多层土时不同的水平抗力，同时提高桩基础设计的效率和精确性，本文采用弹性地基梁有限单元法进行桩基础分析。

1 弹性地基梁有限元法

该方法分析桩-土体系时，采用梁单元模拟桩体，弹性杆单元模拟桩周地基土，分别如图1所示。

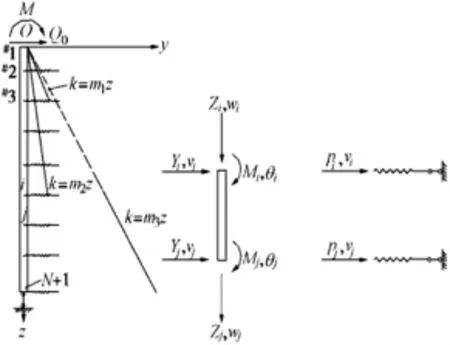
图1 弹性地基有限单元法

对于梁单元，节点编号为 i，j，梁轴线为 z 轴，图中 Qi，Qj，Mi，Mj分别为节点 i，j的剪力和弯矩，υi，υj，θi，θj分别为 i，j节点的位移与转角，pi，pj是 i，j节点处桩侧土单元的弹性反力。可将桩-土体系看成梁杆体系，表示如下：

桩-土体系的边界条件由各弹性地基杆右侧水平位移约束来确定，即：

桩周地基土可视为桩的一系列弹性支座，该支座随着土层深度的不同，刚度发生变化。与上述方程（14）一致，通过上述分析，则将桩-土相互作用的问题离散为分别求解桩体系和土单元体系总位能最小值的问题。其中，桩体系总位能的泛函为：

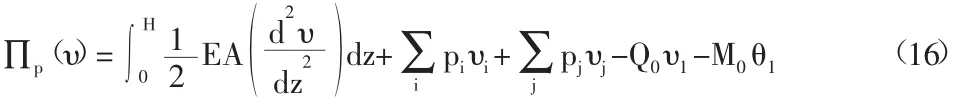
土单元体系的总位能为：

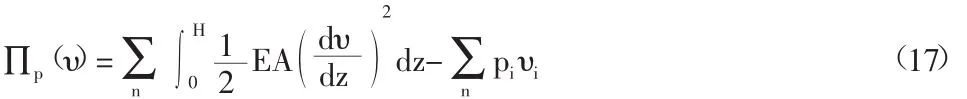
将上述两个方程通过哈密尔特和拉格朗日单元离散，构建差值形函数，将带入泛函式中，求得桩-土体系的求解方程：

式中：K-桩土体系整体刚度；a-桩土体系位移；P-桩土体系荷载。都可以通过桩土体系单元集成得到，求解该方程通过计算得到桩基础的位移。

对于模拟桩侧土体杆单元的刚度矩阵：

式中：A-杆单元的横截面积；l′-杆单元的长度；z-深度；mi-该层土的地基土比例系数；B0-梁单元计算宽度；l-梁单元长度。

求解上述有限元方程，可以求得桩基础各节点的位移，从而可以求得各单元的内力与位移，求解的精度与单元长度的划分有关系[6]。

2 工程实例

本文采用的工程实例为某跨河直线塔基础。该塔位位于河岸漫滩，比河水面高5m，

塔位中心距河30m，地质为非湿陷性黄土，地基土具有中等液化，液化深度11m。该塔受河100年一遇洪水淹没冲刷影响，冲刷深度为12.5m，流速为2.5m/s。设防地质分组为第二组，设防烈度为Ⅷ度0.2g，场地类别为III类场地。

设计该直线塔的正面根开为13.89m，该塔的基础作用力为：T=-1542kN，Tx=193kN，Ty=176kN；N=2042kN，Nx=251kN，Ny=229kN；基础采用桩基础加连梁，桩径为2.0m，桩长44.5m，埋深23.5m，考虑洪水位和冲刷，桩设计露高21m，为了增加桩基础的整体刚度，减小桩顶位移，在桩顶设置连梁。

本文分别采用弹性地基M法和弹性地基有限单元法分别计算桩顶位移，弹性地基M法计算桩顶位移时用的是百合公司开发的《送电线路设计系统2016》（桩基础计算模块），该软件普遍的用于输电线路基础设计中，结果比较可靠。

桩基础桩径2m，在桩顶设置一道连梁时，连梁宽1.6m，高2m。计算时考虑流水100年一遇的冲刷作用，结构受流水的冲刷作用力与基础作用力，计算模型如图2所示，用弹性地基M法计算的桩顶位移为145mm。

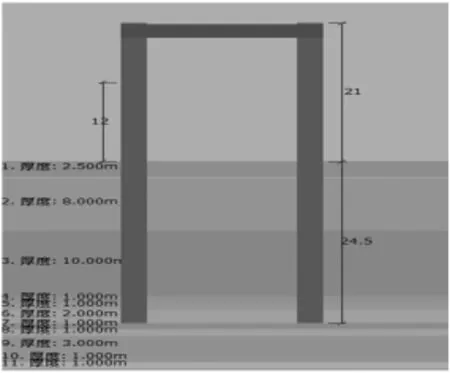
图2 百合软件连梁桩计算模型

用弹性地基有限单元法，在有限元软件中建立该连梁桩的模型，用梁单元模拟桩和连梁，用三维仅受拉或受压单元模拟桩侧土单元，单元网格长度选择0.5m。杆单元的弹性模量ES，随着深度不同取ES=mzbl，ES与深度、m值有关计算模型如图3所示。计算结果得到桩顶位移为154mm。

当采用一道连梁时，桩顶的位移依然较大，不满足规范对框架结构的层间位移的要求，因此考虑设置两道连梁，第二道连梁设置在距桩顶9m的地方，此时，百合软件已经不能计算，只能选用有限元软件计算，计算模型如图4所示，第二道连梁宽1.6m，高2m，距离桩顶9m。

图3 连梁桩有限元计算模型

图4 两道连梁桩计算模型

计算得到桩顶的位移为72.9mm，第二层框架处的位移为43.8mm，可以满足框架结构层间位移的要求。变形如图5所示。由上述的分析可以得出，在计算一道连梁桩顶位移的时候，用弹性地基M法和弹性地基有限元法计算的结果比较接近，说明弹性地基有限元法是可行的。在桩基础设置一道连梁，桩顶位移仍不能满足现行规范时，可以设置两道连梁，设置两道连梁可以有效的减少桩顶位移。

图5 两道连梁桩变形

3 总结

本文介绍了计算水平受荷载桩的弹性地基梁M法，并分析了这种方法不足之处。针对不足之处，采用弹性地基有限单元法来计算桩，用弹性梁单元模拟桩，杆单元模拟桩侧土体，通过有限元法计算单元的位移。以某直流特高压输电线路的直线塔基础为算例，比较地基系数M法和有限元法计算一道连梁桩基础的结果，可以看出两种方法的计算结果较接近，在桩顶位移较大时，设置一道连梁仍不能满足规范要求时，可以设置两道连梁，使桩顶位移能满足规范要求。