平面载荷作用下四边简支层合平板屈曲的有限元模拟

陆旭生

（广东省轻纺建筑设计院有限公司 广东广州 510080）

1 概述

随着建筑业的发展，复合材料凭借其轻质、高强、耐腐蚀和耐老化，在建筑装饰工程中的运用越来越多。由于其一般较薄，在较小的荷载作用下发生屈曲的问题也比较突出。本文研究的层合平板是各种复合材料层合板中最简单又应用最广的一种，以经典层合板理论为基础，而不考虑层间应力和横向剪切影响。

在复合材料结构分析中，已经广泛采用有限元数值仿真分析，本文计算分析采用ANSYS软件，选用Shell99（线性层合结构壳单元）。ANSYS先定义材料性质、铺层角、铺层厚度，然后通过由下到上的顺序逐层叠加组合为复合材料层合结构。假设屈曲以前是薄膜应力状态，不考虑拉弯耦合影响，当平板受平面载荷时，由薄膜状态进入屈曲状态，求引起屈曲的最小载荷。

2 参数设置与模型建立

选取某一复合材料板材，矩形、四边简支，沿着x方向作用均匀平面力x。

图1 均布单向平面压力下的简支矩形层合板

某复合材料板宽b=1m，单层厚度5mm；弹性模量Ex=25MPa，Ey=Ez=1MPa；剪切模量 Gxy=Gxz=0.5MPa，Gyz=0.2MPa；泊松比 νxy=νxz=0.01，νyz=0.25；取平面压力x=1N。

模拟以上材料属性的四边简支层合平板在平面荷载作用下的屈曲，分别建模特殊正交各向异性层合板、对称角铺设层合板、反对称正交铺设层合板、反对称角铺设层合板，考虑铺设层数、长宽比和铺设角这些参数的影响。[1]

3 分析结果

3.1 特殊正交各向异性层合板

分析不同层数和不同长宽比时的屈曲，见表1。

（1）x向半波数=1、y向半波数=1时：

（2）与表1计算结果类似，x向半波数=2、y向半波数=1时，以及x向半波数=3、y向半波数=1时：随着层合板层数的增加，屈曲荷载增大，层数越多，屈曲载荷大小增大越明显；在层数一定时，长宽比a/b对屈曲载荷大小在比值较小时影响明显，并且随着比值增大，屈曲载荷逐渐减小。[2]

表1 不同层数和长宽比时的特征值

（3）分析在层合板层数一定时，不同长宽比a/b下屈曲时特征值的变化情况，对计算数据在相同层数时的特征值结果进行分析。相同层数下，不同长宽比a/b时的特征值大小变化如图2所示。

图 2-a/b 关系

3.2 对称角铺设层合板

分析不同层数和不同铺设角时的屈曲，铺设情况如图3所示。

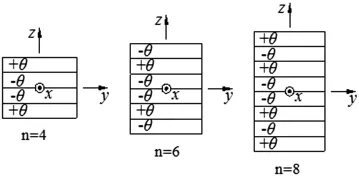
图3 对称角铺设层合板

在对称角铺设层合板铺设角度相同时，随着层合板层数的增加，屈曲荷载增大，层数越多，屈曲载荷大小增大越明显；在层数一定时，铺设角度ϑ对屈曲载荷大小有明显影响，并且随着铺设角度ϑ增大，屈曲载荷先减小，在铺设角度45°左右达到最大值，随着铺设角度ϑ的进一步增大，屈曲载荷开始减小。[3]

3.3 反对称正交铺设层合板

分析不同层数和不同长宽比时的屈曲，铺设情况如图4所示。

图4 反对称正交铺设层合板

计算结果：

表2 不同层数和长宽比的特征值

在反对称正交铺设层合板的长宽比a/b相同时，随着层合板层数的增加，屈曲荷载增大，层数越多，屈曲载荷大小增大越明显；在层数一定时，长宽比a/b对屈曲载荷大小在比值小于1时影响明显；大于1后，随着比值增大，屈曲载荷呈微小的波动形变化。[4]

3.4 反对称角铺设层合板

分析不同层数和不同角度时的屈曲，铺设情况如图5所示。

与对称角铺设层合板的情况类似，在反对称角铺设层合板铺设角度相同时，随着层合板层数的增加，屈曲荷载增大，层数越多，屈曲载荷大小增大越明显；在层数一定时，铺设角度ϑ对屈曲载荷N¯x大小有明显影响，并且随着铺设角度ϑ增大，屈曲载荷先减小，在铺设角度45°左右达到最大值，随着铺设角度ϑ的进一步增大，屈曲载荷开始减小。[5]

图5 反对称角铺设层合板

4 结语

（1）文中运用有限元软件模拟了特殊正交各向异性层合板、对称角铺设层合板、反对称正交铺设层合板和反对称角铺设层合板的屈曲，研究在不同铺设层数、不同长宽比和不同铺设角情况下屈曲载荷的变化，分析屈曲载荷的变化规律。总结铺设层数、长宽比和铺设角这些参数的影响，为复合材料层合板的材料设计提供一些有益参考。

（2）本文研究的是比较简单的层合平板，并且考虑的参数比较有限，存在一定的不足。在以后的分析中可以考虑更多参数、更加复杂的约束、更复杂的形状；以及可以考虑更复杂的铺设情况、复杂载荷的影响；在材料参数方面，可以考虑弹性模量、剪切模量，甚至泊松比的变化对屈曲的影响。