基于塑性应变能理论的边坡动力稳定性研究

崔 笑，张 燎 军，翟 亚 飞，马 天 骁，何 鎏

(河海大学 水利水电学院，江苏 南京 210098)

自郑颖人提出动力强度折减法[1]以来，该方法在边坡动力稳定分析中得到了诸多应用[2-5]。边坡安全系数的获得依赖于所选取的失稳判别准则，但目前学术界和工程界并没有形成统一且为大家所公认的边坡动力失稳判别准则。塑性区贯通、迭代不收敛和关键点位移突变是目前常用的动力失稳判据，但计算结果也常常不一致[6]，因此，部分学者尝试探索新的方法来判断边坡动力稳定状态[7]。考虑到结构失稳是塑性区不断开展直至贯通失稳的过程，其间结构整体塑性应变能不断增大直至突变，可以用塑性应变能表征结构稳定状态。郑东健[8]基于塑性应变能判据研究了拱坝稳定问题；陈倩倩[9]基于塑性应变能判据研究了材料参数对边坡稳定性的影响；李志平[10]基于塑性应变能判据研究了多阶边坡稳定状态，并与理论解进行对比，证明了该判据的可靠性；华成亚[11]将塑性应变能判据应用在三维边坡稳定分析中。但现有关于塑性应变能判据的研究大多集中在静力稳定分析，很少涉及到动力稳定分析。

本文将塑性应变能理论和突变理论应用到边坡动力稳定分析中，通过有限元软件ABAQUS对某边坡进行动力稳定分析，提取边坡震后总塑性应变能并建立与动力折减系数的关系曲线，结合突变理论精准找出震后总塑性应变能突变时对应的动力折减系数，从而确定边坡安全系数。通过对比研究动力工况下塑性应变能判据、塑性区贯通判据和关键点位移突变判据判别机理和计算结果，证明了塑性应变能判据可用于边坡动力稳定分析，且具有一定优势。

1 计算理论与方法

1.1 动力强度折减法

动力强度折减法[1]固定地震荷载不变，把边坡现状抗剪强度参数(c、φ)等比例折减k倍，然后用折减之后的边坡抗剪强度参数(c1、φ1)进行动力时程分析，计算公式如下：

(1)

定义使边坡达到临界动力失稳状态时对边坡抗剪强度参数的折减程度为安全系数。

1.2 塑性应变能理论

在地震荷载作用下，边坡为维持自身稳定会通过应力和应变的方式对自身进行调节。当荷载破坏性超过边坡自身调节能力时，边坡便会失稳破坏。在此过程中，伴随着塑性应变能不断增大直至突变失稳的过程。边坡有限元模型划分为N个单元结构，其中第I个单元所拥有的塑性应变能计算公式[8]为

(2)

对整个模型所有单元的塑性应变能进行累计得到震后总塑性应变能E，计算公式[8]如下

(3)

1.3 基于塑性应变能的尖点突变模型

人为判断突变位置会不可避免地产生误差，通过构造边坡震后总塑性应变能与动力折减系数的尖点突变模型[12]，将边坡动力稳定状态量化为一数学判别式，分析各级动力折减系数下数学判别式与0的大小，从而判定边坡稳定状态，可精确判定边坡动力安全系数。假设边坡震后总塑性应变能E是随动力折减系数k变化的连续函数，将其进行4次泰勒级数展开：

E=f(k)=a4k4+a3k3+a2k2+a1k+a0

(4)

E=b4c4+b2c2+b1c+b0

(5)

式中：

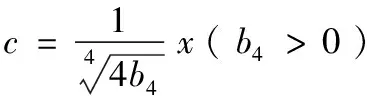
(6)

对式(6)求导，令导数等于0，即得平衡曲面方程为

x3+ux+v=0

(7)

其分差集方程为

4u3+27v2=0

(8)

令

Δ=4u3+27v2

(9)

Δ>0时，坡体处于稳定状态；Δ=0时，坡体处于临界状态；Δ<0时，坡体失稳破坏。

2 算例分析

2.1 工程实例

边坡如图1所示，基于ABAQUS建立其有限元模型，共有节点1 023个和单元947个，单元类型选用CPE4。选用Mohr-Coulomb本构关系，坡脚β=60°。分别在坡顶、坡中和坡脚处选取三个关键点A、B、C。边坡具体材料参数如表1所示。

图1 边坡模型(尺寸单位：m)

表1 边坡材料物理力学参数表

本文以阻尼比5%，动力放大系数βmax=2.5的反应谱合成一组水平向峰值加速度为0.2g和竖向峰值加速度为0.133g的人造地震波。人造波持时20 s，计算步数为2 000，步长0.01 s，如图2所示。

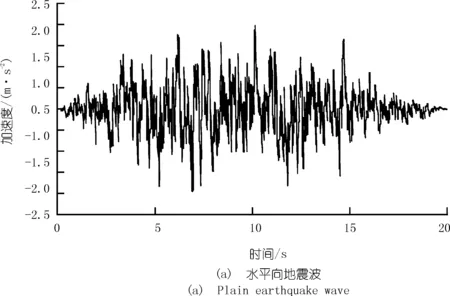
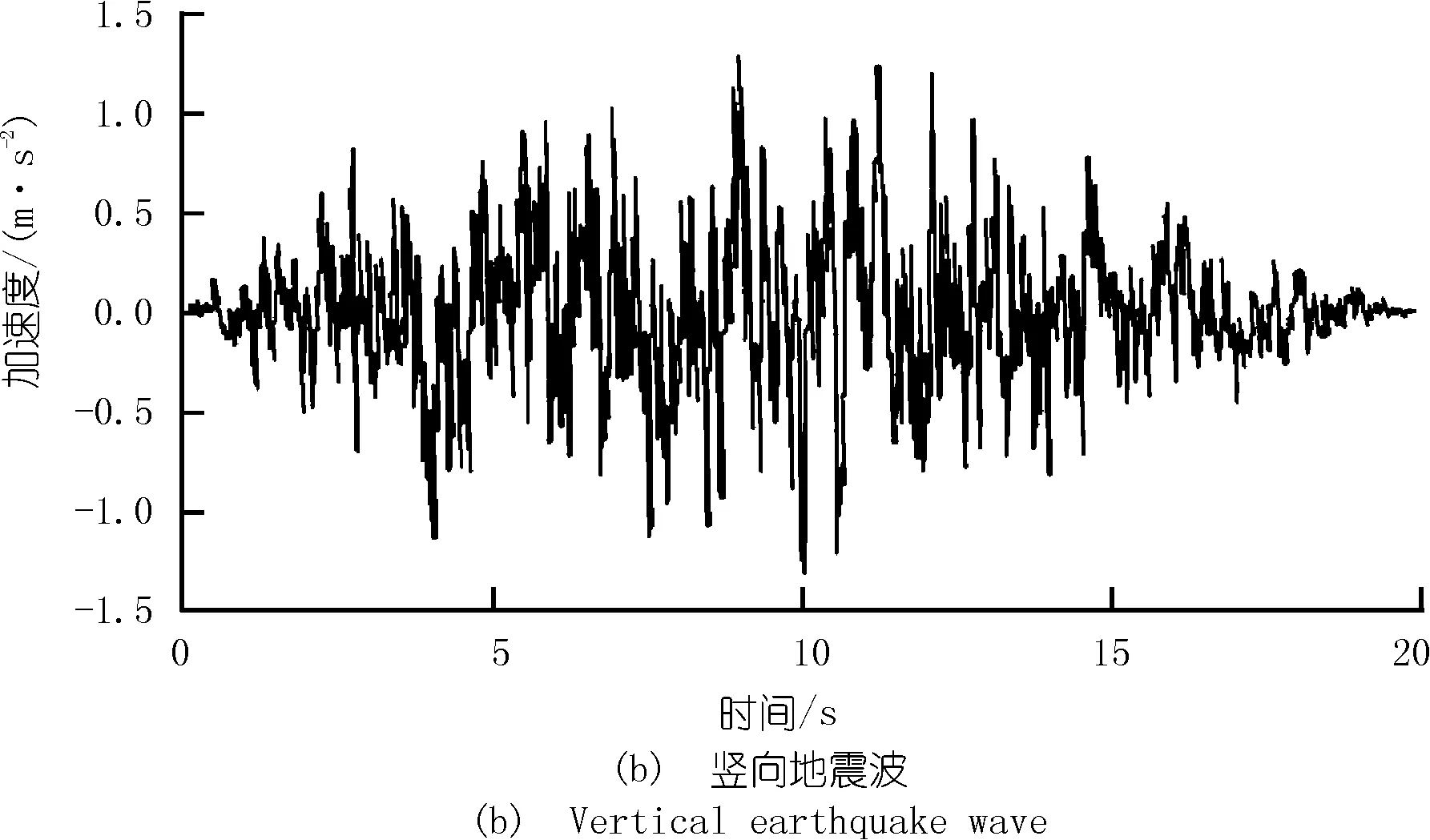
图2 地震加速度时程曲线

本文采用自编程序对底部及四周施加黏弹性边界[13]，以真实反映远域地基辐射阻尼对地震波的影响，并将地震波转换成等效节点力[14]施加在边界上。

2.2 塑性应变能判据

在动力工况下，对边坡岩土材料不断进行软化，将折减k倍后得到的凝聚力c1和内摩擦角φ1输入有限元模型中进行计算。获得多级强度参数下的塑性应变能时程曲线，如图3所示。其中01 s为静力工况，塑性应变能随时间增长沿直线上升；121 s为动力工况，其中15 s和1620 s时地震动较弱，对边坡造成的破坏不大，塑性应变能变化较小，516 s时地震动较强，对边坡造成的破坏程度大，塑性应变能增幅明显。

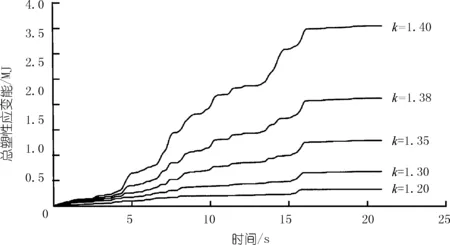
图3 总塑性应变能时程曲线

提取多级动力折减系数下地震结束时的总塑性应变能，绘制E-k关系曲线，如图4所示。从图中可以看出突变点产生在k=1.31.4之间，为了消除人为判断的误差，结合尖点突变理论来定量判断。

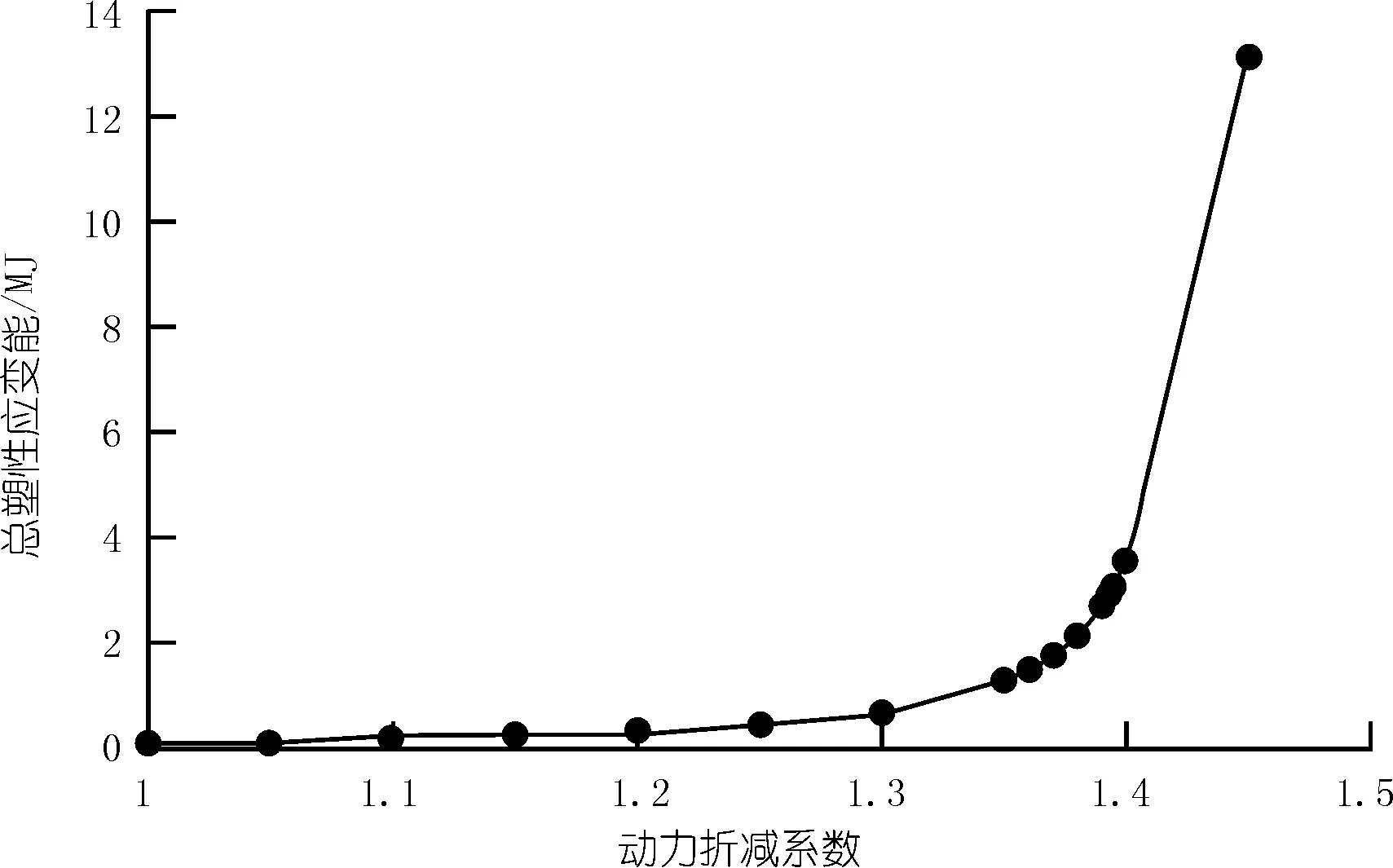
图4 震后总塑性应变能与动力折减系数关系曲线

当动力折减系数k=1.392时，根据式(2)(9)对前12个包括k=1.392共13个动力折减系数进行4次多项式拟合，得到式E=1000.9k4-4617.9k3+7968.1k2-6091.9k+1741简化后代入式(6)得突变模型标准式：

Δ=4u3+27v2=4×(-0.68233)+27×0.25632=0.5

当动力折减系数k=1.393时，同上对前13个包括k=1.393共14个动力折减系数进行四次多项式拟合，得到式：

E=1071.8k4-4951.2k3+8553k2-6546.2k+1872.7

简化后代入式(6)得突变模型标准式：

Δ=4u3+27v2=4×(-0.7353)+27×0.2322=-0.135

结果显示：k=1.392时，Δ=0.5>0，此时边坡结构稳定；k=1.393时，Δ=-0.135<0，此时边坡失稳破坏。所以边坡动力安全系数处于1.3921.393，为了安全考虑，动力安全系数定为1.392。

2.3 塑性区贯通判据

随着岩土材料的不断软化，塑性区从边坡最薄弱的地方慢慢开展直至贯通。如图5所示，当k=1时，塑性区只产生于坡脚一小块区域内，随着k的不断增大，塑性区在慢慢向坡顶扩展；当k=1.32时，塑性区延伸到坡顶，边坡产生了贯通坡顶和坡脚的滑裂带。塑性区贯通判据可直观给出边坡滑裂带所在位置，但边坡是否失稳尚无明确客观判别指标。

图5 边坡塑性应变云图

2.4 关键点位移突变判据

地震荷载不同于静力荷载，在地震动持续时间内荷载处于往复变化状态，因此，边坡位移随时间也会发生往复变化，仅以地震持续时间内某一时刻的关键点位移发生突变不足以判定边坡失稳，但震后残余位移发生突变仍可视为边坡失稳的依据[15]。提取关键点A、B、C的竖向残余位移和水平向残余位移并分别绘制与动力折减系数的关系曲线，如图6所示。

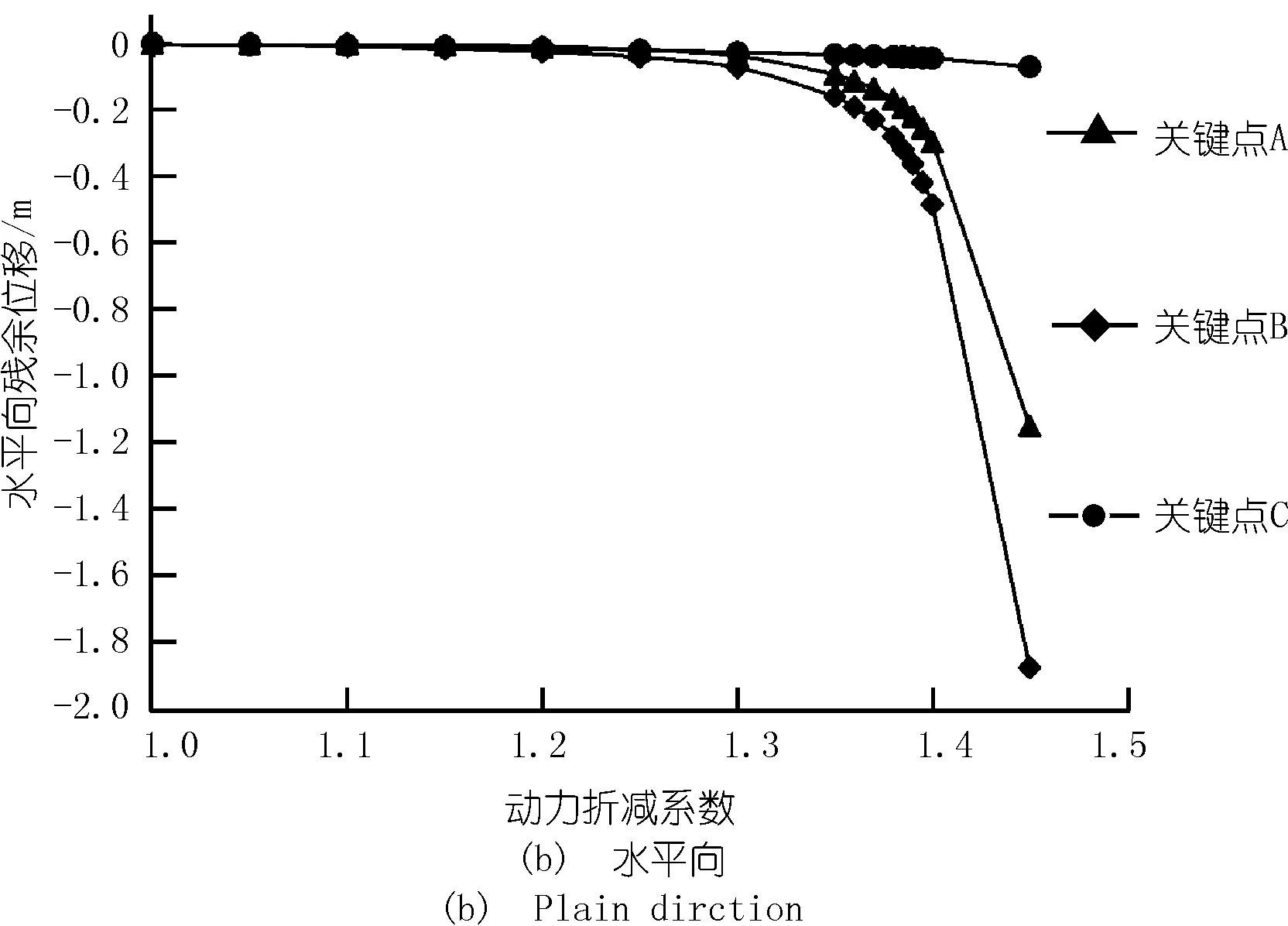
图6 关键点残余位移与动力折减系数关系曲线

从图6可以看出:关键点A和B的竖向残余位移和水平向残余位移均有突变现象产生，关键点C的残余位移并没有突变。根据式(2)(9)以关键点A竖向残余位移或水平向残余位移定量判断突变点位置在1.381.39间；以关键点B竖向残余位移或水平向残余位移定量判断突变点位置在动力折减系数1.371.38间。可以看出，动力工况下关键点位移突变判据判定结果与关键点所选位置密切相关，而与所选位移方向关系不大。

2.5 材料参数对边坡动力安全系数的影响

以上分析说明了塑性应变能判据结果比传统判据更具客观性，但判据结果的准确性还需进一步证明。由文献[16]可知，边坡判据结果会受材料参数影响，为了能有效证明地震荷载下塑性应变能判据结果的准确性。本节改变边坡凝聚力c和内摩擦角φ的大小，以c=100 kPa，φ=20°为基本参数，设置c在80～120 kPa内变化，φ在10°～40°内变化，对比多种材料参数下的塑性应变能判据、塑性区贯通判据和坡顶关键点位移突变判据结果大小，并分别绘制如图7,8所示的关系曲线。

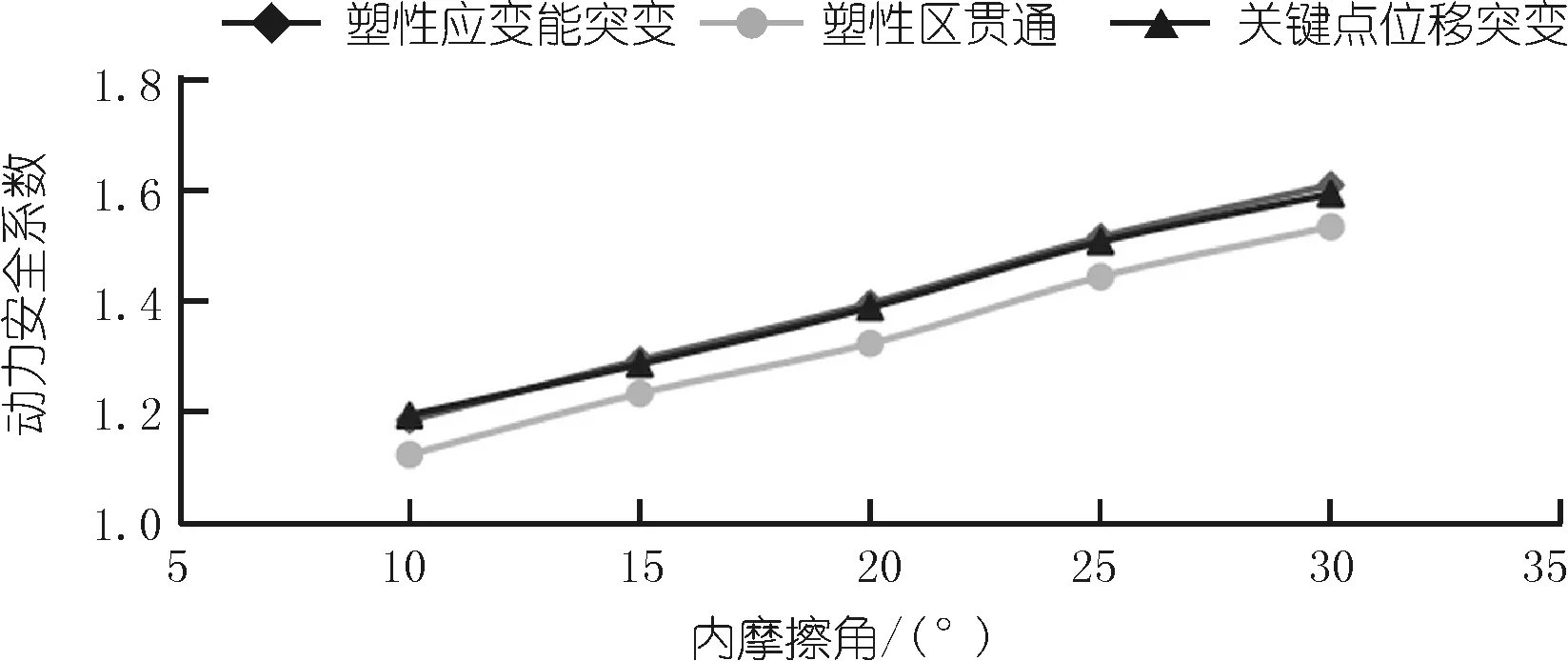
图7 不同内摩擦角下边坡动力安全系数

图8 不同凝聚力下边坡动力安全系数

随着边坡抗剪强度的增加，塑性应变能判据曲线与关键位移突变曲线几乎一致，稍高于塑性区贯通判据曲线，但差距不大，说明塑性应变能判据判定结果与传统判据结果数值上相差不大，以塑性应变能突变为动力失稳判别标准得到的边坡安全系数准确性有保证。

3 结 论

(1)边坡震后总塑性应变能随着折减程度增大而增大，当边坡强度折减到失稳临界值时，塑性应变能便会发生突变，以边坡震后总塑性应变能突变为失稳判别标准，再结合尖点突变理论可以定量给出边坡动力安全系数。

(2)相比于塑性区贯通判据缺乏定量判断指标的缺陷，关键点位移突变判据又受关键点选取位置影响较大，塑性应变能判据以边坡震后整体塑性应变能这一单值标量为动力失稳考察量，不会受过多人为因素影响，判定结果唯一。

(3)在地震荷载作用下，塑性应变能判据结果与关键点位移突变判据给出的结果数值上基本一致，稍大于塑性区贯通判据结果，动力工况下塑性应变能判据结果准确性具有可靠保证。