一种针对函数优化的改进鲸鱼优化算法
郭文涛 张贻红

摘 要:为了提升寻优精度和收敛速度,文章提出了一种改进鲸鱼优化算法。引入混沌Tent映射对猎物包围机制进行改进,提升个体包围速度;设计非线性收敛因子递减机制,均衡全局搜索和局部开发能力;引入混沌Chebyshev映射和高斯扰动机制对气泡攻击进行改进,改善攻击速度慢、精度低的问题,并避免陷入局部最优。通过基准函数测试,证实改进的鲸鱼优化算法可以有效提升寻优精度和收敛速度。
关键词:鲸鱼优化算法;混沌映射;高斯扰动
Abstract:For promoting the optimization accuracy and convergence speed,an improved whale optimization algorithm (IWOA) is raised in this paper. The chaotic Tent map is introduced for improving prey enclosure mechanism and promoting individual enclosure speed. A non-linear convergence factor decreasing mechanism is designed to balance the ability between the global search and local exploration. The chaotic Chebyshev map and Gaussian perturbation mechanism is presented to improve the bubble attack,improve the slow attack speed and low accuracy problems,and avoid falling into the local optimum. The benchmark function test proves that the IWOA can effectively improve the optimization accuracy and convergence speed.
Keywords:whale optimization algorithm;chaotic map;Gaussian perturbation
0 引 言
鲸鱼优化算法(Whale Optimization Algorithm,WOA)是著名学者Mirjalili在2016年提出的一种群体智能算法[1]。WOA模拟了座头鲸的捕食机制,该机制称为气泡网觅食法。座头鲸在捕食包围猎物时,会围绕猎物生成独特的环形气泡,通过群体的搜索、包围、追击和捕食实现优化搜索。WOA由于其原理简单易操作、依赖参数少的特点,已大量应用在多个研究领域,如:无线传感网络覆盖优化[2]、路径规划[3]、特征选择[4]、电力负载调度[5]和群智感知系统[6]等。研究表明,WOA在进行函数目标优化时,其收敛速度、寻优精度两项指标上明显要优于早期的粒子群算法(PSO)、引力搜索算法(GSA)、灰狼优化算法(GWO)。然而,与其他群体智能算法类似,当函数维数递增时,WOA会逐渐显现出收敛变慢、易于陷入局部最优、寻优精度变差的不足。为此,文献[7]利用Logistic混沌映射系统提出了一种改进鲸鱼优化算法,重点改进了初始种群的随机生成方式,使得WOA寻优性能得到了一定提升。文献[8]提出了基于正余弦混沌双弦的改进鲸鱼优化算法,在个体位置更新中融入了自适应机制,有效避免了传统WOA陷入局部最优。文献[9]将模拟退火算法融入传统WOA,对种群的精英个体进行变异更新,避免局部最优解。
结合已有研究成果,为了进一步提升WOA的寻优精度和收敛速度,本文将结合混沌系统和自适应机制,分别针对WOA的初始种群配置以及群体的全局搜索和局部开发能力间的均衡问题进行改进,设计一种改进的鲸鱼优化算法(IWOA),综合提升其寻优性能。并通过不同维度规模的基准函数的测试,证明改进的算法可以有效处理大规模函数寻优问题。
智能电网大数据主要来自电力检测、变电站、电表中收集的海量数据,尤其在笔者所在的国家电网有限公司大数据中心,大数据分析项目组每天都会监测收集来自各个电网管理系统中的海量数据,这类大数据具有规模大、种类多、干扰数据多、异质等特点。为了从电网运行过程中生成的海量数据中提炼出有益于电网系统的分布式管理、有效进行电力分配的数据,需要对这些海量数据进行数据挖掘与分析。对于数据挖掘而言,对原始数据进行特征选择与聚类分析是必不可少的预处理步骤。而作者提出的IWOA即可通过转换为二进制寻优形式,对相关性高、黏度大的数据进行特征选择,以提高后续分类算法的数据分类准确率。
1 一种融合混沌与扰动机制的改进鲸鱼优化算法
1.1 WOA的运行原理
WOA的捕食行为可划分为包围、气泡攻击和搜索猎物三个阶段进行。
(1)包围猎物。座头鲸包围猎物并朝着最优搜索代理更新自身的位置,以此完成猎物包围过程。其数据模型为:
(2)气泡攻击。气泡攻击可分为收缩包围和螺旋位置更新两种方法。收缩包围通过收敛因子从2递减至0实现,搜索个体的新位置可定义在其初始位置与当前最优个体间的任意位置,即A在[-1,1]间的任意位置。螺旋位置更新公式为:
(3)搜索猎物。鲸鱼个体通过随机选取的个体完成对猎物的搜索过程,模型定义为:
1.2 IWOA的设计与实现
1.2.1 猎物包围机制的改进
当决策概率q<0.5,且|A|<1时,表明鲸鱼个体正在向猎物收缩包围。由式(1)可知,搜索个体与目前之间的距离主要由参数A、C决定。由式(2)和式(3)可知,计算两个参数时,除了收敛因子a之外,参数值主要受随机量r1和r2控制。由于完全随机量不具有搜索空间内的遍历性和随机规律性,会导致猎物包围速度慢、精度低。在此,IWOA利用混沌映射系统生成两个随机量,提升个体对猎物的包围速度。混沌系统具有非线性、对初值敏感、遍历性及整体稳定但局部不稳定的特征。目前,常用的混沌映射系统包括Logistic、Tent、ICMIC、Bernouilli shift、Chebyshev和Sine映射等。其中,Logistic映射的特点是中间取值较均匀,但量少,两端取值较多,总体均匀分布不足;Tent映射存在小周期和不稳定周期点;ICMIC映射则对初值具有最强的敏感性;Bernouilli shift与Tent相似;Chebyshev寻优时间太长;Sine映射寻优精度最低。综合考虑,改进算法利用Tent映射生成随机变量。Tent映射公式為:
1.2.2 收敛因子的非线性改进
由WOA的运行机制可知,当|A|<1时,搜索个体将依据式(1)作位置更新,进行包围猎物,完成局部开发过程。当|A|≤1时,搜索个体将依据式(6)作位置更新,进行猎物搜索,完成全局搜索过程。而A值则由收敛因子a确定,即WOA的局部开发与全局搜索间的切换由a确定。依据式(4)可知,收敛因子将从2呈线性递减至0,这表明,在迭代初期,收敛因子取值更大,探测步长更大,可以实现全局搜索。而在迭代后期,收敛因子取值更小,探测步长减小,可以实现更为精细的局部搜索,使算法收敛。然而,两种搜索模式的切换并不是完全线性的,改进鲸鱼优化算法利用一种非线性收敛因子递减方式,定义为:
1.2.3 气泡攻击机制的改进
由式(5)可知,气泡攻击机制中,搜索个体的位置更新主要受随机值l的影响,而l为[-1,1]间的随机值。同样的原因,由于完全随机量不具有搜索空间内的遍历性和随机规律性,会导致对猎物的攻击速度慢,精度低。在此,IWOA利用混沌映射系统生成随机量。由于l∈[-1,1],而Chebyshev映射符合该取值空间,虽然其寻优时间较长,但可使l分布更加均匀。混沌Chebyshev映射定义为:
1.2.4 气泡攻击的扰动机制
由式(5)可知,搜索个体进行气泡攻击由当前的最优个体Xp引领。为了避免迭代后期寻优过程陷入局部最优,需要对当前最优个体进行位置扰动,避免产生局部最优解。为此,IWOA引入一种面向最优个体的高斯扰动机制,新的最优个体的位置定义为:
2 数值仿真
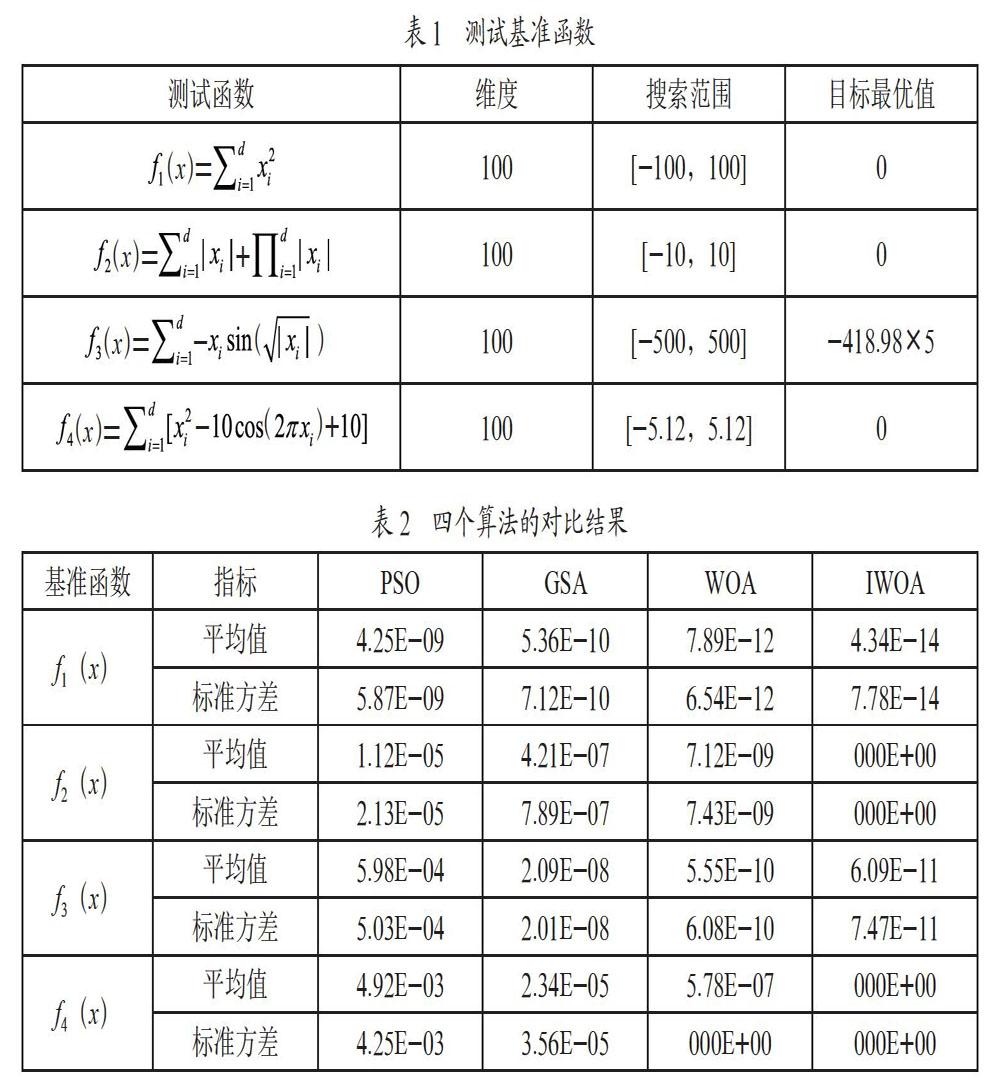
为了测试IWOA的性能,本节选取四个基准测试函数进行数值仿真。四个基准函数说明如表1所示,f1(x)和f2(x)是单峰函数,f3(x)和f4(x)是多峰函数。设置IWOA的种群规模为40,总体最大迭代次数400,收敛因子初值为2,终值为0,高斯扰動因子为0.5。实验结果取20次仿真结果的均值,使结果更具一般性。实验在Matlab平台上进行。PSO、GSA、WOA作性能对比。选取寻优结果(包括平均值和标准方差)和适应度作为性能评估指标。
表2是四个算法的寻优结果对比情况。依据数据统计结果,IWOA不仅在四个基准函数测试中均得到了所有算法中最接近最优值的均值和标准方差结果,而且还在函数f2(x)、f4(x)中已经找到函数最优解。这说明在高维度函数条件下,IWOA可以适用于单峰函数和多峰函数的函数优化求解,并且具备更高的稳定性。也说明IWOA中所采用的混沌机制、非线性收敛因子调整机制以及对于优良个体的高斯扰动机制可以有效提升算法性能,提升寻优精度。
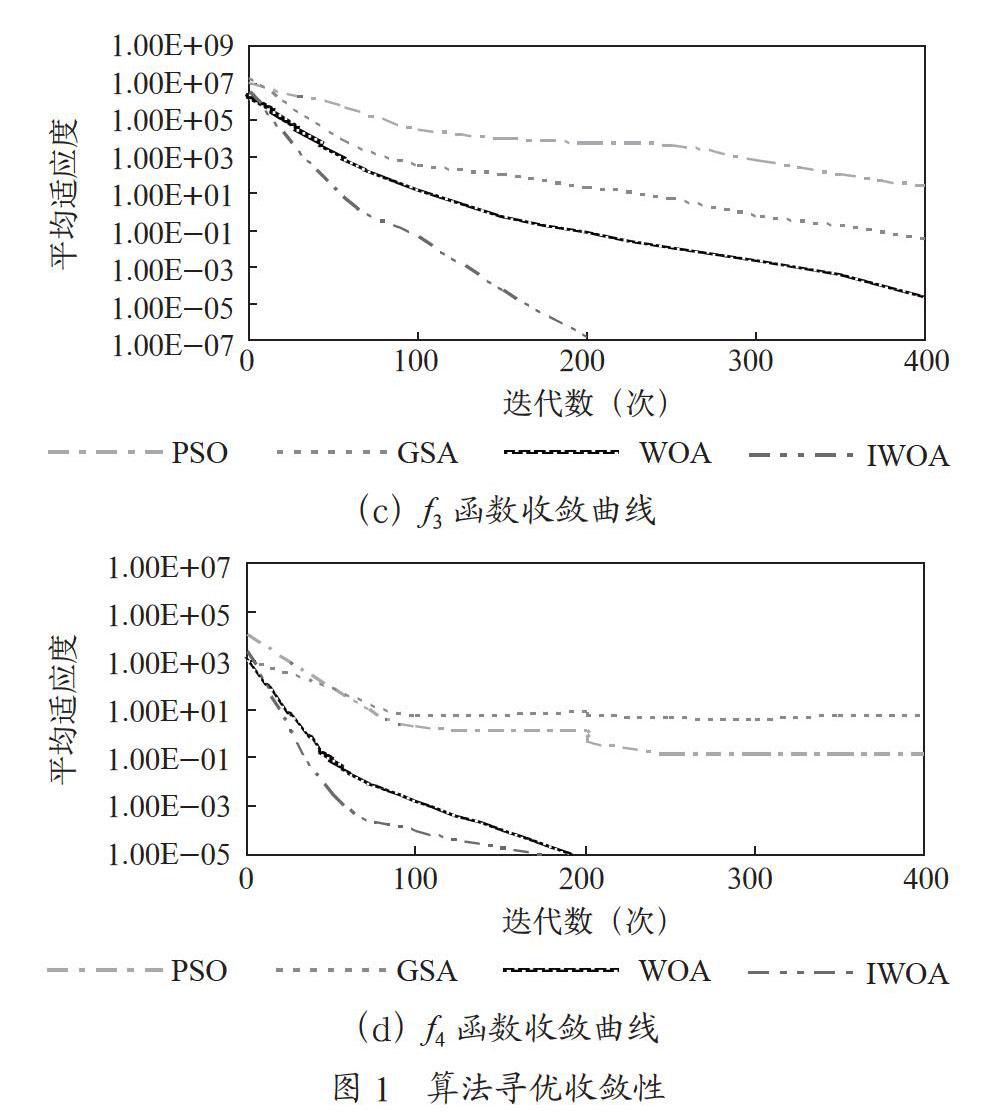
图1是四种算法在四个基准函数上测试的寻优收敛曲线图。总共执行400次算法迭代。由四条曲线趋势可知,IWOA能以更快的速度找到对应最优适应度的最优解。对比算法中,PSO和GSA都要迭代近400次后得到最优解,而WOA和IWOA可以提前获得最优解。这表明IWAO中所采用的改进机制可以加快算法寻优速度,并提高寻优精度。
3 结 论
本文提出了一种改进鲸鱼优化算法(IWOA),首先,算法引入混沌Tent映射对猎物包围机制进行改进,有效提升了包围速度;其次,算法设计了一种基于非线性的收敛因子递减机制,有效均衡了全局搜索和局部开发能力;最后,算法引入混沌Chebyshev映射和高斯扰动机制对气泡攻击进行改进,有效改善攻击速度慢、精度低的问题,并避免陷入局部最优。通过一系列基准函数测试,证实IWOA可以有效提升寻优精度和收敛速度。进一步研究可以尝试在工程优化问题中验证改进算法的可行性和效率。
参考文献:
[1] MIRJALILI S,LEWIS A. The Whale Optimization Algorithm [J]. Advances in Engineering Software,2016,95:51-67.
[2] 宋婷婷,张达敏,王依柔,等.基于改进鲸鱼优化算法的WSN覆盖优化 [J].传感技术学报,2020,33(3):415-422.
[3] 王迪,金辉.贪婪鲸鱼优化算法求解带时间窗的快递末端配送路径问题 [J].计算机应用与软件,2020,37(6):263-268+315.
[4] 王生武,陈红梅.基于粗糙集和改进鲸鱼优化算法的特征选择方法 [J].计算机科学,2019,47(2):44-50.
[5] 徐建中,晏福.改进鲸鱼优化算法在电力负荷调度中的应用 [J].运筹与管理,2020,29(9):149-159.
[6] 袁姝,周朝荣,杨正清,等.群智感知系统中基于鲸鱼优化算法的任务分配 [J].计算机工程与设计,2020,41(7):2031-2037.
[7] 张永,陈锋.一种改进的鲸鱼优化算法 [J].计算机工程,2018,44(3):208-213+219.
[8] 刘竹松,李生.正余混沌双弦鲸鱼优化算法 [J].计算机工程与应用,2018,54(7):159-163+212.
[9] 褚鼎立,陈红,王旭光.基于自适应权重和模拟退火的鲸鱼优化算法 [J].电子学报,2019,47(5):992-999.
作者简介:郭文涛(1988—),男,汉族,山西大同人,工程师,硕士,研究方向:智能信息处理;张贻红(1987—),男,汉族,湖南娄底人,工程师,硕士,研究方向:大数据处理。

