新视角下人体域网模型的二阶统计量


摘 要:以往人体区域网络的应用都是一阶统计,文章采用可以跨越多个链路和人体区域的人体区域网网络,对其的无线信号进行二阶统计,并通过对特征参数的统计和测量,将得到的二阶特征频谱进行比较。最后基于一个庞大的,每天150小时的人体连接的数据库,这些数据证明了电平交叉率、平均衰减/非衰减持续时间相对于中值或平均信道增益方面给定值的缺陷。同时还对两参数的对数正态分布进行拟合分析,能够更简单、准确的对其进行描述。
关键词:人体区域网络;信道建模;无线电传播;二阶统计
Abstract:The application of human body area network(BAN)is the first-order statistics in the past. The article uses the second-order statistics of the wireless signals of BAN which can span multiple links and body areas. Through the statistics and measurement of characteristic parameters,the obtained second-order characteristic spectra are compared. Finally,based on a huge database of 150 hours of human connections per day,these data prove the shortcomings of the level crossover rate,the average attenuation/non-attenuation duration relative to the median or given value in terms of average channel gain. At the same time,the logarithmic normal distribution of the two parameters is fitted and analyzed,which can describe it more simply and accurately.
Keywords:body area network;channel modeling;radio propagation;second-order statistics
0 引 言
近些年由于人体区域网络(BAN)的发展比较迅猛,作者的专业与对通信领域结合比较多,因此将对其进行深入研究。
BAN是一種位于人体周围的传感器/执行器网络,2012年IEEE发布了802.15.6的人体区域网络的标准[1],具有跨时代意义。在无线电传播和开发可靠的信道模型方面,已经有了巨大的进步,人体区域信道强度和人体周围显著的时变阴影效应对可靠性的影响被证明是特别重要的[2,3],本文采用文献[4,5]中应用于一阶统计量的方法,针对影响可靠性的三个特别重要的二阶统计量其进行分析。具体二阶统计量为:
(1)衰落持续时间:信道增益低于任何给定电平的持续时间,可用于确定在给定发送/接收链路上可能无法成功传输分组的时间,其中信道增益与路径损耗成反比。
(2)类似的非衰减持续时间:信道增益超过阈值的持续时间,表示成功分组传输的时间长度。
(3)电平交叉率(LCR):信号强度来自从上到下从任意给定信号电平交叉的平均速率(特别是在平均信道增益[6]),可用于推断衰落速率。
衰减(和非衰减)的持续时间和电平交速率高度依赖于人体各区域的信道强度[2,3,6]。
在邻近的无线电传播特性中,描述小尺度衰落的一阶统计量被用于生成电平交叉间隔和衰落持续时间[7,8],例如,特别是用于BAN的传输中[2,3,9]。需要注意的是,在各种早期的无线电传播文献中,已经对电平交间隔和衰减持续时间的直接统计特性进行过描述[10,11]。根据这些传输特性,本文会进一步理清这些重要的二阶统计量的直接表征的值,并通过提供一个完整的度量来比较直接表征和二阶统计量的值。然后,会从“开放访问”数据库中,获得每天150小时的人体连接的信道增益,并应用此方法。
1 模型表征
首先,我们先回顾了文献[5]中的拟合优度函数,对于p参数θp={θ1,…,θp}应用于n个样本的数据x是:
其中,ε{}是模型和数据之间误差的增长函数,{}是参数个数的增长函数。“最优”模型将{}最小化。
在这里选择一个自然参考点用来对模型进行评估,它可能最大限度地使用赤池信息准则(AIC)[12]或贝叶斯信息准则(BIC)[13]来拟合的简单(或复杂)统计分布。该参考点是二阶数据集在电平交叉间隔、衰减持续时间或非衰减持续时间下的实验的直方图,也就是说,给定这些持续时间或时间间隔的M个数据集,选择具有中心的Tt∈x的T个直方图箱,并且对于每个数据集m=1,…,M,求t=1,…,T的单变量的实验直方图Hm(Tt)。这是具有m×t自由参数直接二阶“模型”,在满足标准(连续)概率密度函数模型0≤Fm(x)<+∞时,方程式形为:
同时对数计算用于计算复杂度。不使用统计中的样本数n,因为这在分析的数据集中是一致大的[5,15]。
2 实验数据
使用人体的“每日”的BAN开放访问数据集,使用文献[15]中描述的可穿戴无线电。由于信号在时间上数据是连续的,链接m=10个(左髋→胸/左腕/右踝/左踝/右髋/头;胸→左腕/右腕/右踝/左踝),并采集了10个成人受试者的数据。发现实验柱状图(使用T=80时间箱)和统计适合于单个数据集(每个链路)和集合(聚合),应用于衰减持续时间、非衰减持续时间和电平交叉间隔的平均值和中值的信道增益。该数据全体包含了1.17亿个信道增益样本,每个链路包含的数据分布并不均匀,最多有2 400万个样本(从左髋到右踝的链接),最少的只有530 000个样本(胸部至右踝关节链接),平均每个链接包含1 200万个样本。
值得注意的是:对模型的最优描述,在每个链接和凝聚的所有情况下,根据二阶逻辑AIC准则、衰减/非衰减持续时间、电平交间隔与以2为底的对数正态统计分布,的时间序列具有很好(更简单)的拟合性。图1和图2表示了不同模型选项误差下ε和复杂度的关系,用于分别评估关于信道增益均值和中值的电平交叉间隔。图3对比了关于信道增益中值的衰落持续时间,图4展示了关于信道增益中值的非衰落持续时间下,误差与复杂度的关系。这里根据等效优度是由ε+=常数得到的,并且所谓“更好”的模型将更接近原始点,由于每条链路平均值的不确定性(参数P=M=10),在给定单均值的情况下,为了更好地显示其他模型选项的相对误差,我们扩展了图1~4虚线标注的部分。
如图1~4所示,所有数据集的经验直方图误差为零,但对于P=MT来说其复杂度过高同样,同样,对于P=T下的组合直方图也很复杂,并且存在一定的误差。图1和图2中使用较为简单的凝聚平均电平交叉间隔(平均信道增益或信道增益中值)。或者图3和图4中使用较为简单凝聚平均衰落持续时间或凝聚平均非衰减持续时间(信道增益中值)所造成的误差也非常大。对于图1、图2中的电平交叉间隔,以及图3中的衰落持续时间,优度可以通过对所有链路进行一个以2为底的对数正态拟合,得到了较为明确的优化。但在图4中不明显,这是由于对于每条链路如果采用以2为底的对数正态进行拟合和凝聚直方图拟合相比,凝聚拟合的误差ε略有增加。然而根据我们的标准,仍然使用以2为底的对数正态凝聚拟合进行优化。
对于电平交叉间隔、衰落持续时间和非衰落持续时间,信道平均增益和增益中值的最佳对数正态凝聚拟合的数据汇总可以观察到,对于各自的统计数据,无论衰减持续时间、非衰减持续时间还是电平交叉间隔,平均信道增益或者是信道增益中值的,从对数均值和对数标准差参数角度来说,尽管平均信道增益通常大于中值增益几分贝,最佳对数正态拟合都非常相似。
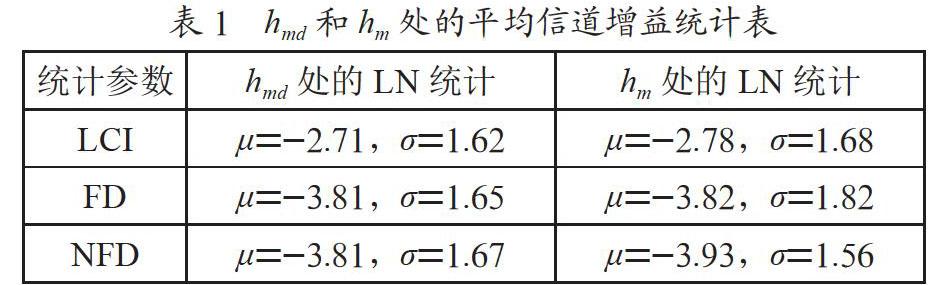
表1为最佳对数正态(LN)凝聚拟合结果。参数:μ为对数平均值,σ为对数标准差。统计:LCI为电平交叉间隔(LCR的逆);FD为衰减持续时间;NFD为非衰减持续时间。表中,信道增益中值表示为hmd,平均信道增益hm捕获的统计数据。
图5给出了平均信道增益的凝聚水平交叉间隔数据的对数正态拟合结果,平均信道增益的电平交叉间隔与对数均值为-2.78、对数标准差为1.68的对数具有良好的拟合特性。图6中显示了左髋到右腕的人体连接上,信道增益中值的衰减持续时间分布的对数正态拟合结果,平均信道增益的电平交叉间隔与对数均值为-3.73、对数标准差為1.67的对数分布拟合良好。图7中显示了相同左髋到右腕链接的信道增益中值的非衰减时间的对数正态拟合,平均信道增益的电平交叉间隔与对数均值为-3.74、对数标准差为1.74的对数分布拟合良好。从实验直方图和拟合对数正态分布可以看出,对于衰减持续时间和非衰减持续时间,根据上述分析可以得出,图5中的水平交叉间隔的持续时间要大于图6和图7中的一个链接所表示的持续时间数据,这表明对数正态凝聚拟合的对数均值较高,适合于电平交叉间隔。
3 结 论
本文扩展了一阶统计量的绝对拟合优度,并将这种拟合优度测度直接应用于衰落持续时间、非衰落持续时间和平交率的重要二阶统计量。该度量结合了建模误差和复杂度的度量(通过参数数目P的对数),清楚地表明了采用一阶统计量来描述上述时间统计的不足。证明了对数正态最佳拟合(对数正态分布适合于描述衰落持续时间、非衰落持续时间和水平交叉间隔)是一个可靠和有效的模型,并具有较低的复杂度。该方法已经应用于典型的BAN设备接收灵敏度水平的均值和信道增益中值,同时也适合扩展到更低的信道增益阈值。后续还将考虑该方法扩展到其他“开放访问”数据(例如,在跑步机上跑步的受试者捕获的数据,或在室内环境中行走的受试者进行离体测量的数据)。
参考文献:
[1] IEEE. IEEE Standard for Local and metropolitan area networks-Part 15.6:Wireless Body Area Networks:35.100.10 35.110-Physical layer Networking [S/OL].IEEE,2012:1-271(2012-02-29).https://doi.org/10.1109/IEEESTD.2012.6161600.
[2] SMITH D B,ZHANG J,HANLEN L W,et al. A simulator for the dynamic on-body area propagation channel [C]// IEEE Antennas & Propagation Society International Symposium.IEEE,2009.
[3] COTTON S L,SCANLON W G. Characterization and Modeling of the Indoor Radio Channel at 868 MHz for a Mobile Bodyworn Wireless Personal Area Network [J].IEEE Antennas & Wireless Propagation Letters,2007(6):51-55.
[4] LEWIS D. 802.15.6 Call for Applications-Response Summary [EB/OL].(2008-11-13).https://mentor.ieee.org/802.15/dcn/08/15-08-0407-05-0006-tg6-applications-summary.doc.
[5] SMITH D B,HANLEN L W,LAMAHEWA T A. A new look at the body area network channel model [C]// European Conference on Antennas & Propagation.IEEE,2011.
[6] SMITH D B,MINIUTTI D,HANLEN L W,et al. Dynamic Narrowband Body Area Communications:Link-Margin Based Performance Analysis and Second-Order Temporal Statistics [C]// 2010 IEEE Wireless Communication and Networking Conference.Sydney:IEEE,2010:1-6.
[7] RISSANEN J. Modeling by shortest data description [J].Automatica,1978,14(5):465-471.
[8] WAX M,KAILATH T. Detection of signals by information theoretic criteria [J].IEEE Transactions on Acoustics,Speech,and Signal Processing,1985:33(2):387-392.
[9] PATZOLD M,LAUE F. Level-crossing rate and average duration of fades of deterministic simulation models for Rice fading channels [J].IEEE Transactions on Vehicular Technology,1999,48(4):1121-1129.
[10] MIMAKI T,SATO H,TANABE M. A study on the multi-peak properties of the level-crossing intervals of a random process [J].Signal Processing,1984,7(3):251-265.
[11] RICE S O. Distribution of the Duration of Fades in Radio Transmission:Gaussian Noise Model [J].Bell System Technical Journal,1958,37(3):581-635.
[12] AKAIKE H. A new look at the statistical model identification [J].IEEE Transactions on Automatic Control,1974,19(6):716-723.
[13] SCHWARZ G. Estimating the Dimension of a Model [J].The Annals of Statistics,1978,6(2):461-464.
[14] HARTLEY R V L. Transmission of information [J].The Bell System Technical Journal,1928,7(3):535-563.
[15] HANLEN L,CHAGANTI V,GILBERT B,et al. Open-source testbed for Body Area Networks:200 sample /s ec,12 hrs continuous measurement [C]//2010 IEEE 21st International Symposium on Personal,Indoor and Mobile Radio Communications Workshop.Instanbul:IEEE,2010:66-71.
作者簡介:李冉(1982—),男,汉族,江苏徐州人,教师,副教授,硕士,主要研究方向:计算机网络通信技术、计算机网络管理、计算机操作系统、计算机网络安全技术、人工智能技术。

