具有分布时滞的广义系统的容许性条件
孙 欣, 白雅迪
(沈阳师范大学 数学与系统科学学院, 沈阳 110034)
0 引 言
广义系统又称为奇异系统,是实际系统的一种客观表示,常见于电力系统、生物系统、航空航天系统、机械工程系统和经济系统等实际系统中。广义系统可以用来表述系统的更多性能特征,和正常系统相比,它的应用更为广泛。1989年,Dai[1]出版广义系统专著《Singular Control Systems》,首次采用状态空间方法系统介绍广义系统理论,为研究广义系统理论提供了重要参考。
许多实际系统过去的状态影响系统当前的状态,即系统的演化趋势不仅与系统当前状态有关,而且也可能与过去状态有关。具有时滞的系统称为时滞系统。时滞是工程实际中普遍存在的现象,可能影响系统稳定性、导致系统性能下降,近年来关于时滞系统的研究很多。
若系统中的时滞为过去一段时间系统变量的积分,这样的时滞称为分布时滞。分布时滞系统模型常用于热力学、生态学或流行病学。下面给出线性分布时滞系统:
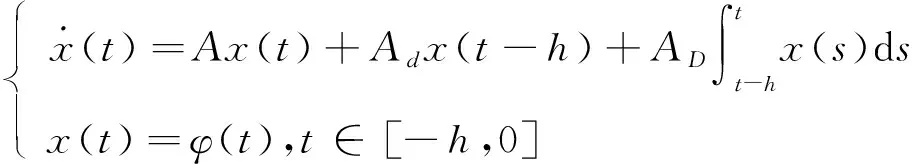
(1)
可以看出,分布时滞系统中的时滞具有在整个时滞区间的分散性影响。分布时滞能够更精确地描述系统,揭示事物变化的本质。近年来,有关分布时滞系统的研究取得了一些进展。顾克勤[2]改进了构造离散Lyapunov泛函的方法,在处理导数项时应用Jensen不等式和变量消元法,得到分布时滞系统的稳定性判据。Zheng和Frank[3]研究了状态变量中存在分布时滞的不确定线性系统的鲁棒稳定性和鲁棒镇定问题,给出了分布时滞系统鲁棒稳定条件,所提出的方法应用在了液体单推进剂火箭发动机燃烧室的稳定性上。Cheng和Zheng[4]针对具有分布时滞的不确定中立系统,研究了鲁棒稳定和镇定问题,使用积分不等式技术和广义系统方法,以线性矩阵不等式的形式给出鲁棒稳定时滞依赖条件和鲁棒镇定设计方法。
通常稳定性作为系统控制的最基本要求。对于连续广义系统,在正则、无脉冲的前提下,系统具有稳定性,从而系统是容许的。因此研究具有分布时滞广义系统的容许性问题具有重要意义。对于时滞系统,降低系统稳定性条件的保守性至关重要。常用的方法是构建一个合适的L-K泛函[5-6]。何勇等[7]添加一些时滞交叉项,提出了增广L-K泛函,这些交叉项有助于减少时滞系统稳定性条件的保守性[8]。对于广义时滞系统的容许性研究,构建L-K泛函时,现有结果主要由非积分项、一重积分项和二重积分项组成[9-13]。为了进一步减小具有分布时滞的广义系统容许性条件的保守性,可以构造一个合适的增广L-K泛函,并且在泛函中加入三重积分项,进一步降低结果的保守性。
在降低时滞系统稳定性条件的保守性方面,除了L-K泛函的构造外,L-K泛函求导后产生的导数项的估计也至关重要。早期利用Park不等式、Moon不等式以及模型变换等来对L-K泛函的导数项进行处理。在此基础上,吴敏等[14]提出了自由加权矩阵法,何勇等[15]对其进行了改进,自由加权矩阵法对于降低时滞系统稳定性条件的保守性起到了重要的作用。后来,Jensen不等式[16]被广泛采用。2013年,Seurt等[17]基于傅里叶理论提出了一个新的Wirtinger不等式,获得了使时滞系统稳定更大的时滞上界。2015年,Seurt等[18]提出Bessel-Legendre不等式,它比Jensen不等式和Wirtinger不等式保守性小,可以得到时滞系统保守性更小的稳定性条件。
本文利用Bessel-Legendre积分不等式对L-K泛函的导数项进行处理,推导出具有分布时滞的广义系统保守性更小的容许性条件,与同类文献相比本文采用的方法获得了更大的时滞上界。
标记说明
1 问题描述
考虑分布时滞广义系统
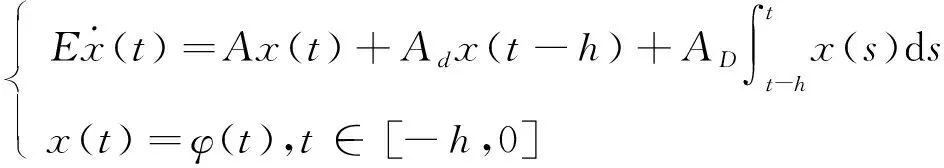
(2)
式中:x(t)∈n是系统状态向量;矩阵E∈n×n,且rank(E)=r≤n;A,Ad,AD∈n×n是已知的常数矩阵;h是满足约束条件h>0的常数时滞;φ(t)是连续可容的向量值初始函数。
定义1[1]
1) 若det(sE-A)≠0,则称矩阵对(E,A)是正则的;
2) 若degdet(sE-A)=rank(E),则称矩阵对是无脉冲的;
3) 若det(sE-A)=0的根全部具有负实部,则称矩阵对(E,A)是稳定的;
4) 若矩阵对(E,A)是正则、无脉冲的、稳定的,则称矩阵对(E,A)为容许的。
定义2[1]
1) 若矩阵对(E,A)是正则、无脉冲的,则称系统(2)是正则、无脉冲的;
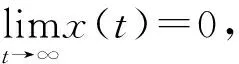
3) 若系统(2)是正则、无脉冲、稳定的,则称为容许的。
引理1[1]如果矩阵对(E,A)是正则、无脉冲的,那么存在2个可逆矩阵G,H∈n×n,使得
(3)
引理2[18]对于矩阵R∈n×n,R>0,参数b>a,向量函数x:[a,b]→n,则以下不等式成立:
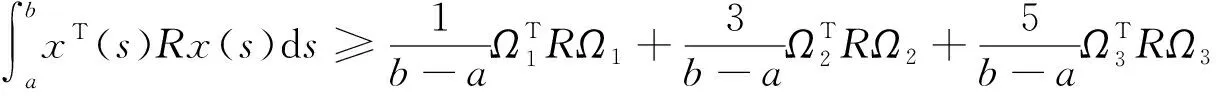
(4)
其中
其中
其中
2 主要结果
定理考虑分布时滞广义系统(2)。对于参数h>0,若存在正定矩阵P=(Pij)∈4n×4n,Pij∈n×n,正定矩阵Q,R1,R2,M∈n×n, 任意矩阵W∈n×(n-r), 列满秩矩阵L∈n×(n-r), 并且满足ETL=0,满足下面线性矩阵不等式:
其中
式子中ei∈n×5n,ei=[0n×(i-1)n,In,0n×(5-i)n],i=1,2,3,4,5。则分布时滞广义系统(2)是容许的。
证明 首先,证明分布时滞广义系统(2)是正则、无脉冲的。因为rank(E)=r (8) 令 线性矩阵不等式(7)可以写成 (12) 其中 #表示与接下来的讨论无关的内容。 根据式(12)得到 因为Q,R1,R2,M是正定矩阵,所以 式(14)分别左乘和右乘HT、H,得到 (15) 容易得到 (16) 所以A22是非奇异的。否则,假设A22是奇异的,存在非零向量φ∈n-r,使得A22φ=0。由合同变换,得到与式(16)相矛盾。所以A22是非奇异的。因此,矩阵对(E,A)是正则、无脉冲的。根据定义2,分布时滞广义系统(2)也是正则、无脉冲的。因此存在另外2个非奇异矩阵n×n使得 (17) 令 又 (22) (23) 不难看出系统(23)和系统(2)在稳定性上是等价的。接下来证明系统(23)是稳定的。 构造如下增广L-K泛函为 (24) 其中 对V(t)求导,得到 定义 (29) 应用引理2,可以得到 (33) 其中 (35) 根据Lyapunov稳定性定理可知,系统(23)是稳定的,所以系统(23)是容许的,所以分布时滞广义系统(2)是容许的。从而定理结论成立,证毕。 注释1 定理基于Lyapunov第二方法,利用Bessel-Legendre积分不等式,通过构造适当形式的L-K泛函,得到了新的分布时滞广义系统容许性的判定条件。 注释3 若rank(E)=r=n,这时分布时滞广义系统(2)就变为分布时滞系统(1): 由定理能得到分布时滞系统(1)的时滞相关稳定性的条件。 推论考虑分布时滞系统(1)。对于参数h>0,若存在正定矩阵P=(Pij)∈4n×4n,Pij∈n×n,正定矩阵Q,R1,R2,M∈n×n。满足下面线性矩阵不等式: 其中 式子中ei∈n×5n,ei=[0n×(i-1)n,In,0n×(5-i)n],i=1,2,3,4,5。则分布时滞系统(1)是稳定的。 例1 考虑如下连续广义分布时滞系统: 其中 表1 系统允许最大时滞Table 1 The maximum allowable upper bounds of delay 当AD为零矩阵时,例1即为文献[24]中的数值算例。利用Matlab的LMI工具箱求解,表1分别列出文献[12,22-24]及定理算出系统允许最大时滞hM。 从表1可以看出,与同类文献相比,定理获得了使得广义分布时滞系统容许的更大时滞上界,说明定理具有较小的保守性。 例2 考虑如下分布时滞系统: 其中 通过Matlab的LMI工具箱求解,得到系统允许最大时滞hM=2.778 4,说明所提出方法的有效性。 本文研究了分布时滞广义系统的容许性问题。为了降低容许性条件的保守性,构造了增广的L-K泛函,引入了三重积分项;并且利用二阶Bessel-Legendre不等式、三阶Bessel-Legendre积分不等式和双重二阶Bessel-Legendre积分不等式来处理L-K泛函求导后的导数项;以线性矩阵不等式的形式给出了具有分布时滞的广义系统的容许性条件。数值算例说明了本文所用方法的有效性和优越性。

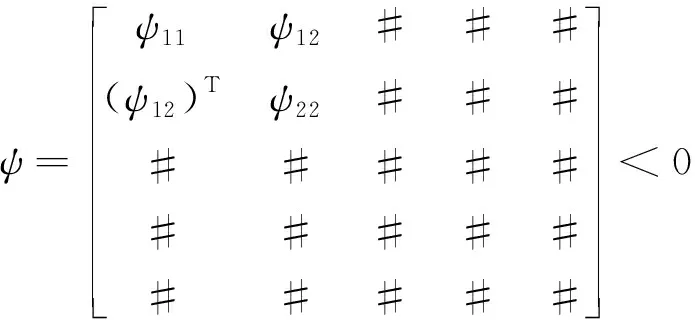
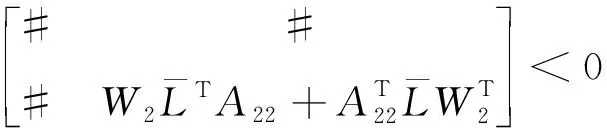
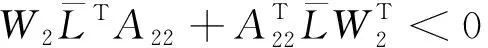
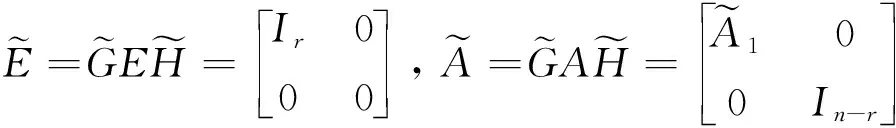
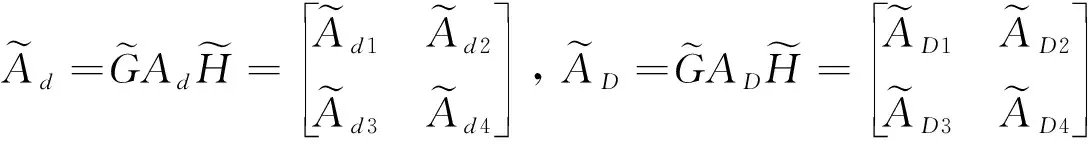
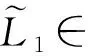

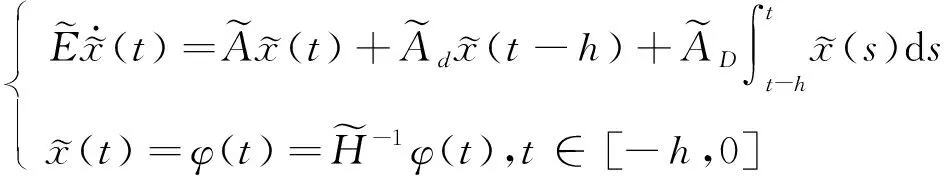
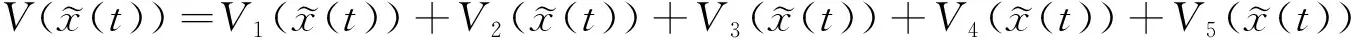
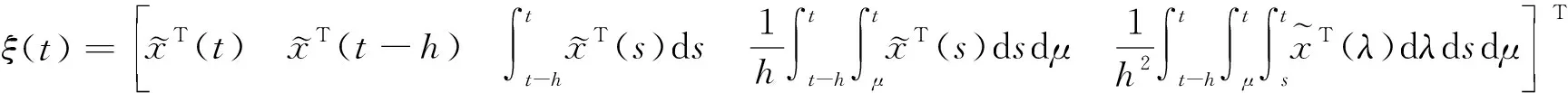
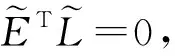
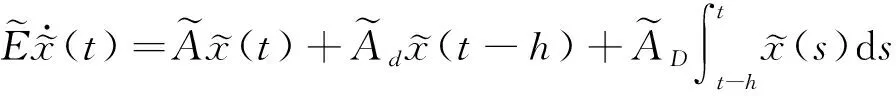
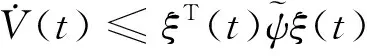
3 数值算例

4 结 语

