梯形区域极点配置静态输出执行器的容忍区间

姚 波, 魏一丹, 王福忠

(1. 沈阳师范大学 数学与系统科学学院, 沈阳 110034;2. 沈阳工程学院 基础教学部, 沈阳 110136)

0 引 言

在控制理论中,可靠控制的设计增加了系统的保守性,如果系统正常运行,则会有资源发生浪费,为了避免这一现象,我们研究故障对系统的影响程度,如果故障引起的波动信号在容忍区间内,则系统不受干扰正常运行。文献[1]综合介绍并展望了有关于线性系统区域稳定可靠控制的设计。文献[2-3]分析了条形区域、圆盘区域不确定项的容忍区间,文献[4-5]将极点配置在扇形和梯形区域,设计静态输出反馈可靠控制装置,文献[6-7]提出关于线性系统区域极点配置的理论依据。文献[8-9]在传感器和执行器发生故障的前提下,设计使极点配置在指定区域内的控制器。文献[12]根据极点配置提出容忍区间的概念,文献[13-14]提出了系统硬件冗余度的算法,利用增加故障部件的方法使系统稳定,但这种方式在处理通道以及部件排列时,通常需要反复实验才能确定,为了避免可靠控制造成的的资源浪费、硬件冗余方式的繁琐实验,容忍区间的算法分析则具有一定的研究意义。

本文针对线性系统,将静态输出反馈与区域极点配置相结合,在执行器某条通道添加增益偏差,通过信号波动对系统的影响,得到了容忍区间的概念与算法。设计人员利用容忍区间算法,进一步设计较好的系统,降低设计成本。

1 问题描述

考虑线性定常系统:

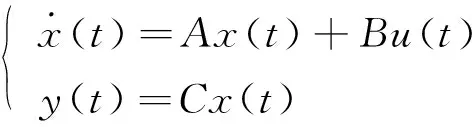
(1)

其中x(t)∈Rn为系统的状态向量;y(t)∈Rm为系统的输出向量,u(t)∈Rm为系统输入向量;定常矩阵A∈Rn×n为系统矩阵、B∈Rn×n为控制矩阵、C∈Rm×n为系统的测量行满秩矩阵。

对于线性系统(1),设计静态输出反馈控制器:

u(t)=Ky(t)

(2)

此时闭环系统为

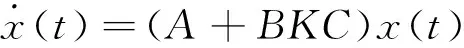
(3)

执行器的单一通道增益偏差模型为

uf=Miu(t)

(4)

考虑模型(4),系统(1)的闭环系统为

(5)

其中Ac(fi)=A+BMiKC。

引理1 已知S是n×n正定对称矩阵(m≤n),G是适维行满秩矩阵,则矩阵GSG′可逆。

分析:证明GSGT可逆,等价于证明方程GSGTX=0只有零解。

证明 设GSGTX=0

∴XGSGTX=0

∴(GTX)TS(GTX)=0

∵S是n×n正定对称矩阵

∴GTX=0

∴GGTX=0

又∵GGT可逆,则X=0

综上,方程只有零解,GSGT可逆,证毕。

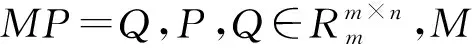
引理3[9]矩阵A的所有特征值,均配置在由h1,h2组成的垂直条形区域D(h1,h2)(图1)内的充要条件是:存在正定对称的矩阵X,使得下式成立。

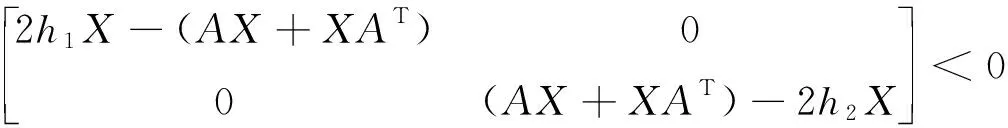
(6)

引理4[9]矩阵A的所有特征值,均配置在夹角为2θ的扇形区域D2θ(如图2)内的充要条件是存在正定对称的矩阵X,使得下式成立:

(7)

图1 垂直条形区域D(h1,h2)Fig.1 Vertical strip areaD(h1,h2)

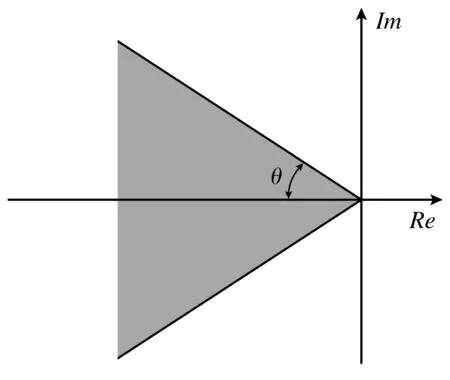
图2 扇形区域D2θFig.2 Sector areaD2θ

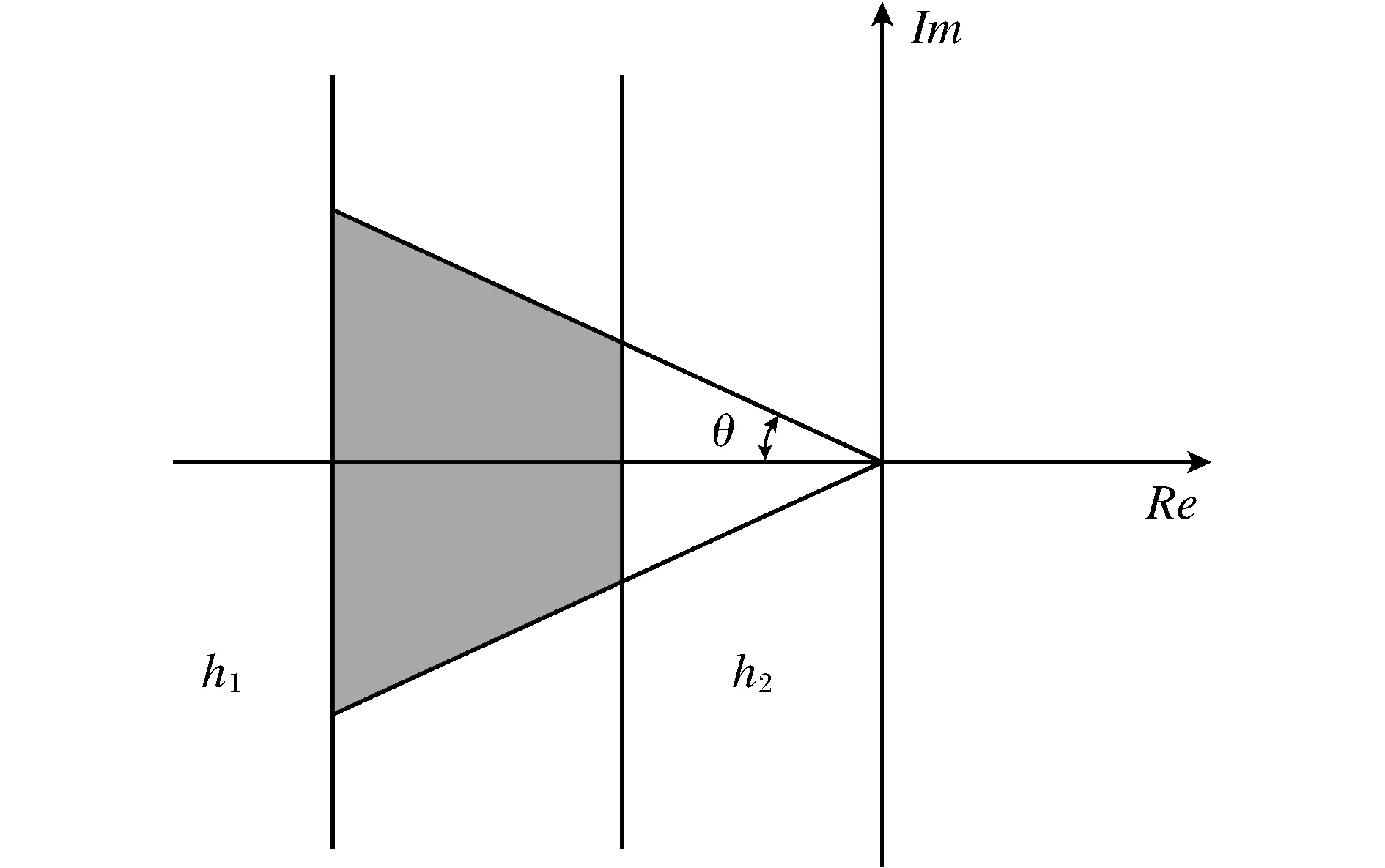
图3 梯形区域DFig.3 Ladder areaD

引理5[10]存在增益矩阵K,使极点配置到公共区域D(图3)内的充要条件是:存在正定对称矩阵X,矩阵P满足下列线性矩阵不等式组:

成立。

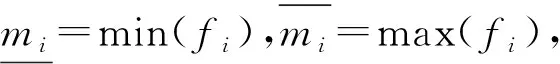
2 主要结果

定理1 对于闭环系统(3),存在静态输出反馈控制器(2)使其满足引理5的充分条件为对于正定对称矩阵X和矩阵U使得下列线性矩阵不等式LMIs:

存在(X,U),则控制器为K=UW-1。

其中:Ω1=AX+BUC,W可以由WC=CX求得。

证明 由引理5可知把闭环系统(3)极点配置梯形区域内须满足

整理可得

令U=KW

故有

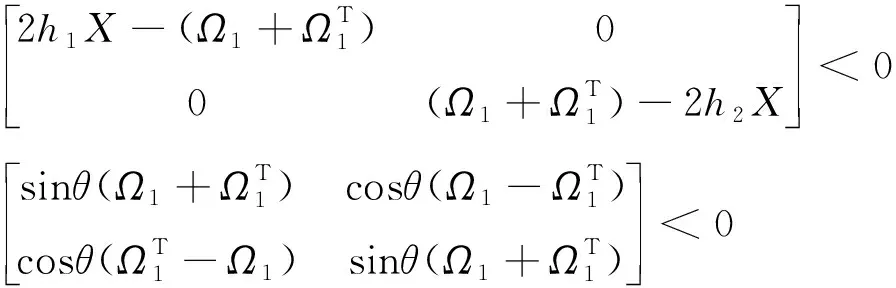
也就是不等式(10)。

其中WC=CX,Ω1=AX+BUC。

下证W可逆。

对等式WC=CX等号左右两边乘以C′得:WCC′=CXC′

则W=CXC′(CC′)-1

即证CXC′可逆。

由引理1可知CXC′可逆,故W可逆。

定理得证。

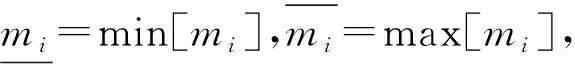
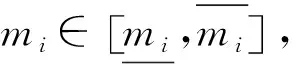
3 数值仿真

考虑如下系统:

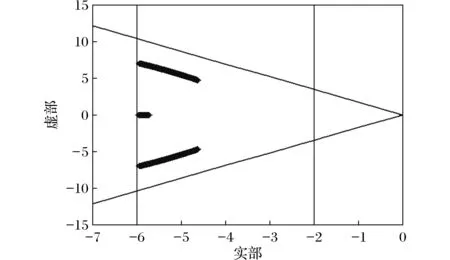
图4 第一通道增益偏差为[0.973,1.183]时极点恰好完全分布在梯形区域Fig.4 When the first channel gain deviation is [0.973, 1.183], the poles are exactly distributed in the trapezoidal area

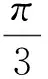
现在考虑添加第一条通道增益偏差,使极点全部配置在梯形区域内,根据定理1可知,容忍区间的确定就是分别取|xij-t|-l≤0,yij≤+xijtanθ≤0的最优解,当执行器第一条通道增益偏差为容忍区间f1∈(0.973,1.183)时,观察极点在梯形区域的分布情况如图4所示。闭环系统极点全部配置在梯形区域内,这表示增益信号引起的波动在[0.973, 1.183]内,并不影响执行器的正常运行。

利用执行器在第一通道增益偏差[0.973, 1.183]时的闭环系统矩阵特征值,做进一步检验。如图5和图6所示,当执行器第一条通道增益偏差为[0.973,1.183]时,闭环系统矩阵特征值符合定理1的结论。因为执行器在第一条通道增益偏差为[0.973,1.183]时,极点恰好完全配置在梯形区域,根据定义即执行器第一条容忍区间为f1∈(0.973,1.183)。

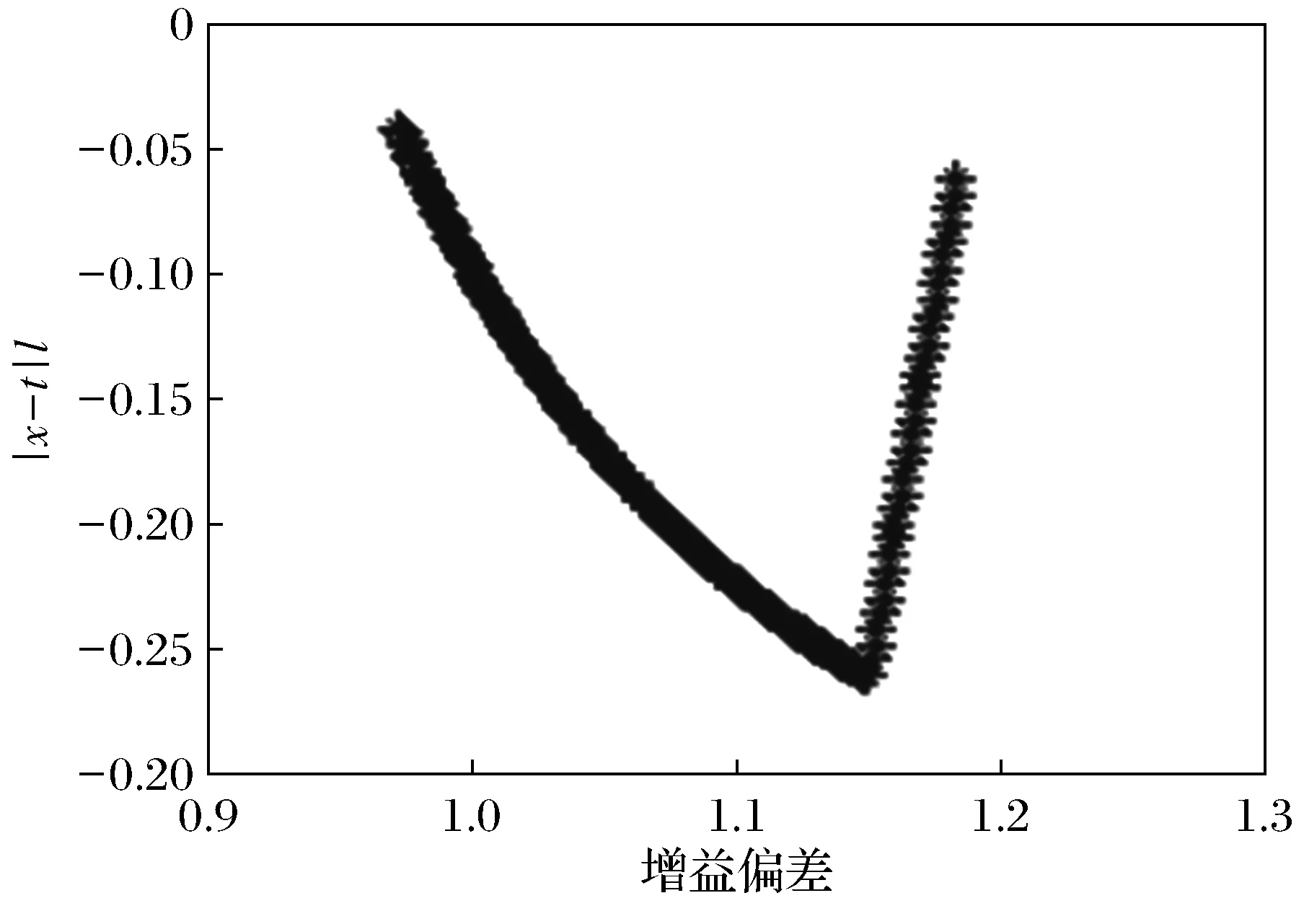
图5 第一通道增益偏差为[0.973,1.183]时极点分布与条形边界的关系

图6 第一通道增益偏差为[0.973,1.183]时极点分布与条形边界的关系

现在考虑添加第二条通道增益偏差,使闭环系统极点全部配置在梯形区域内。根据定理1可知,容忍区间的确定就是分别取|xij-t|-l≤0,yij≤+xijtanθ≤0的最优解,当执行器第二条通道增益偏差为容忍区间f2∈(0.6,1.005)时,观察极点在梯形区域的分布情况如图7所示。

如图7所示,执行器第二通道增益偏差[0.6,1.005]时,闭环系统极点全部配置在梯形区域内,增益信号引起的波动在[0.6,1.005]内,执行器正常运行。利用执行器在第二通道增益偏差[0.6,1.005]时的闭环系统矩阵特征值。

如图8和图9所示,当执行器第二条通道增益偏差为[0.6,1.005]时,闭环系统矩阵特征值符合定理1的结论。执行器在第二条通道增益偏差为[0.6,1.005]时,极点恰好完全配置在梯形区域,根据定义执行器第二条容忍区间为f2∈(0.6,1.005)。

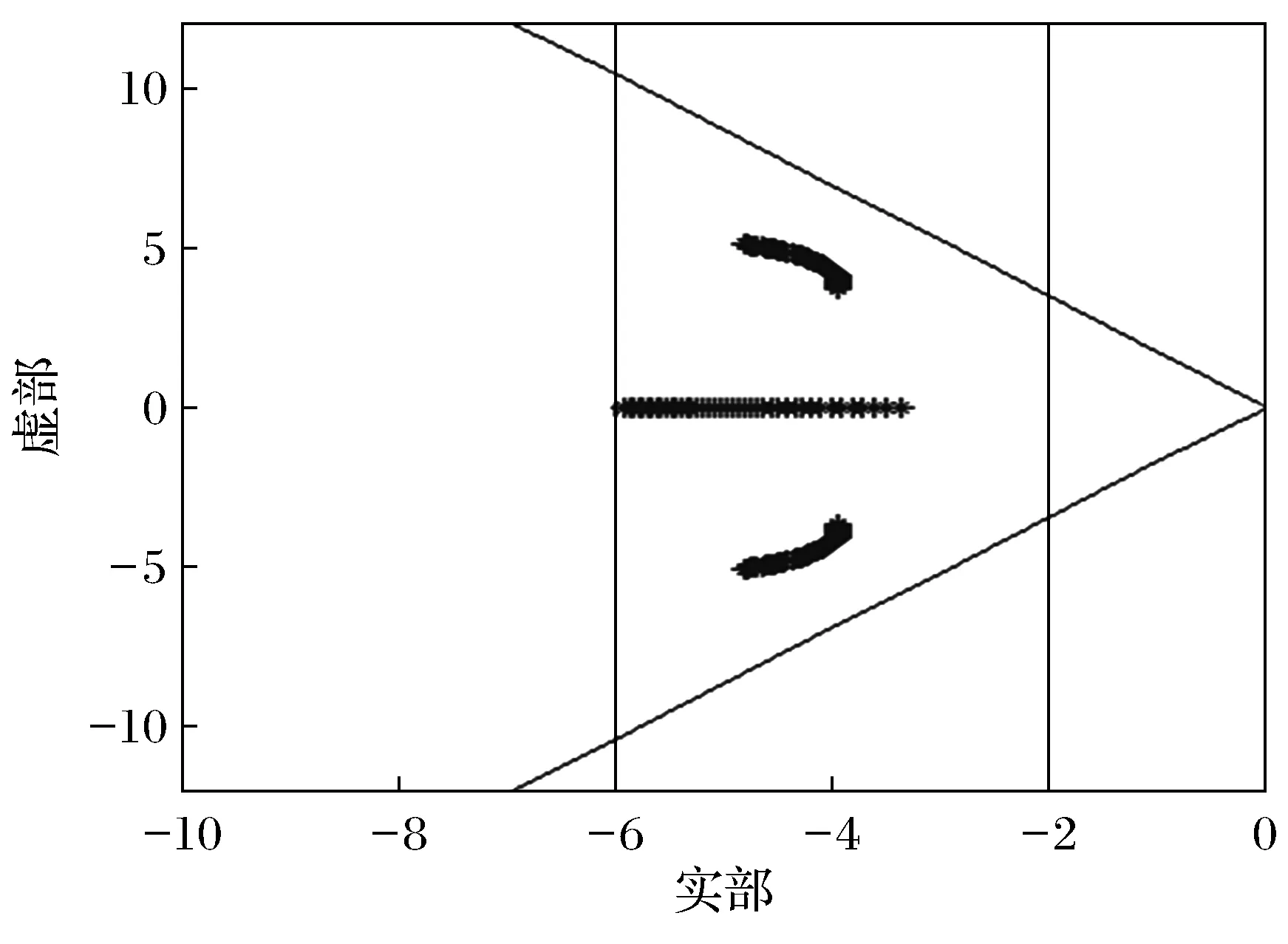
图7 第二通道增益偏差[0.6,1.005]极点恰好完全在梯形区域

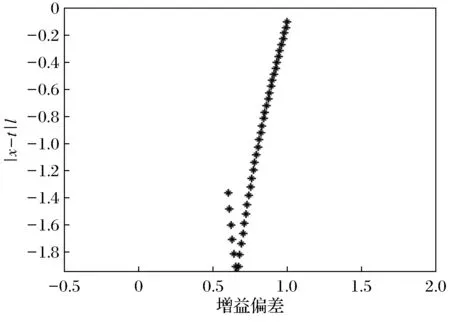
图8 第二通道增益偏差[0.6,1.005]时极点分布与条形边界的关系

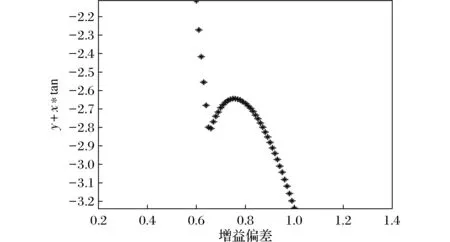
图9 第二通道信号增益偏差[0.6,1.005]时极点分布与扇形边界的关系Fig.9 The relationship between the pole distribution and the sector boundary when the second channel signal gain deviation [0.6,1.005]

根据定义1,执行器各通道容忍区间越大,则增益偏差越大,在保证系统性能时容许信号波动范围越大;相反,执行器各通道容忍区间越小,则增益偏差越小,在保证系统性能时容许信号波动范围越小。

4 结 论

本文主要研究正常系统的故障部件对系统的影响,结合了静态输出反馈控制,将添加增益偏差后的闭环系统极点,配置在梯形区域内,根据增益偏差引起的信号波动,观察极点的分布状况,给出执行器容忍区间的概念和算法。设计者如果可以掌握容忍区间,则在设计过程中就可以减少成本资源,并且保证系统较高的安全性能。文中的数值仿真得到的极点配置图像证明了结论有效可行。