钢栈桥桩顶梁截面ANSYS简化对其力学性能的影响
谢晓鹏,王娟,窦国涛,李晗,高波
(1.郑州航空工业管理学院 土木建筑学院,河南 郑州 450046;2.郑州大学 水利与环境学院,河南 郑州 450001;3.江苏省交通工程集团有限公司,江苏 镇江 212100)
0 引 言
钢栈桥是一种为运输材料、设备、人员而修建的临时桥梁设施,钢栈桥上部通常采用桁架结构,上部相同考虑下部,一般采用钢管桩[1]。国内外众多学者[2-8]针对钢栈桥的力学性能进行了一系列研究。刘永锋[9]采用通用有限元软件ANSYS,根据工程特点及荷载情况,对既有结构方案进行强度、稳定性验算,对组成栈桥的各构件轴向刚度进行参数分析,包括上下弦杆、竖腹杆、斜腹杆的轴向刚度改变对整体结构性能的影响;尹栋佳等[10]通过某大桥临时工程钢栈桥的施工方案,详细介绍了临时钢栈桥上部结构的设计分析过程。利用空间计算软件ANSYS和MIDAS/Civil建立栈桥有限元分析模型,结合某大桥施工中拟投入的施工机械和车辆荷载,对栈桥上部结构进行承载力验算和稳定性分析。在栈桥分析验算过程中,总结一些具有实际工程意义的结论,提出一些关于钢栈桥设计技术的建议。王海云等[11]以某选煤厂钢结构栈桥为例,分析钢栈桥设计中遇到的问题,并利用大型通用有限元分析软件ANSYS,对该栈桥进行了静力分析及校核,分析结果表明结构稳定可靠,且能满足设计要求。
以上研究针对钢栈桥进行分析时,通常采用ANSYS软件进行有限元分析,然而钢栈桥桩顶梁一般采用工字钢截面形式,工字钢翼缘截面为变截面形式,在ANSYS中建模复杂,本文将其简化成矩形,然后进行静力和动力作用下的受力分析,并和原截面进行对比。
1 工程背景
本文中钢栈桥为山西垣曲至河南渑池高速公路黄河大桥中混凝土结构的施工临时措施,在三门峡大坝和小浪底大坝的中部,位于小浪底库区。栈桥总计1座,分为南、北两岸,北岸长270 m,南岸长1 050 m。栈桥桥墩采用钢管桩基础,以40号墩钢管桩为例(图1),桩长68 m,钢管桩壁厚采用D1 000×10 mm进行设计,纵横向剪力撑均采用 D500×8 mm的钢管进行连接,桩顶顺桥方向布置双拼I45a工字钢桩顶梁;桩顶梁中间横桥向布置双拼I50a工字钢承重梁;承重梁上架设贝雷梁。双拼I45a工字钢和双拼I50a工字钢截面形状如图2所示,截面尺寸见表1。

图1 钢管桩现场照片

图2 双拼I45a和I50a工字钢截面形状

表1 双拼I45a和I50a工字钢截面尺寸
由于工字钢截面形状复杂,在ANSYS中自定义截面较为困难,本文将其简化成H型钢截面,截面尺寸见表2,截面形状如图3所示,分析在静力荷载(自重荷载)和动荷载(风荷载)作用下,两者的受力区别,为后续类似工程提供参考。

表2 双拼I45a和I50a简化后截面尺寸

图3 双拼I45a和I50a简化后截面形状
2 ANSYS有限元建模
钢管桩、剪力撑、桩顶梁和承重梁均采用beam188单元模拟,该单元是一个二节点的三维线性梁,适用于分析细长的梁,元素是基于Timoshenko梁理论的,具有扭切变形效果[12-14]。钢管桩和剪力撑截面采用圆环截面,桩长68 m,钢管桩尺寸为D1 000×10 mm,纵横向剪力撑均尺寸为 D500×8 mm,和实际尺寸保持一致,弹性模量2.06×1011Pa,密度7 800 kg/m3,泊松比0.25,钢管桩的入土深度25 m,对于此部分区域节点,施加全约束,如图4所示。桩顶梁材料属性和钢管桩一致,截面采用以下2种工况,如表3所示,其有限元模型如图4所示。

表3 工况设置
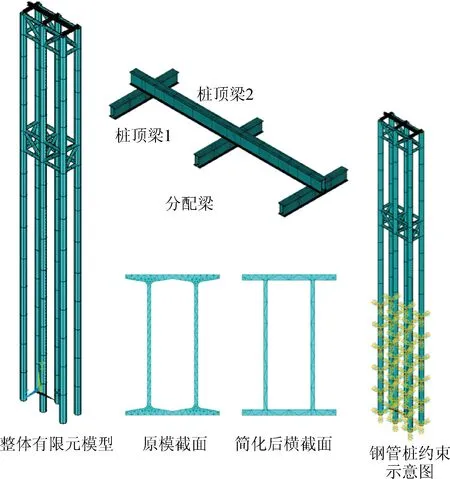
图4 有限元模型
Fig.4 Finite element model
3 静力作用分析
3.1 静力荷载计算
如图5所示,承重梁上边架设贝雷梁,贝雷梁采用321型标准钢桁梁拼装,钢桁梁每节长3 m,高1.5 m,构件材料为16Mn,每片钢桁梁质量270 kg,全桥钢桁梁设置12排,钢桁梁横向间距为(45×3+90×2+135+90×2+45×3)cm。贝雷梁上边架设横梁,分配梁采用I25a热轧普通工字钢,每根长9 m,横梁下部与贝雷梁上弦杆采用抱箍固定,上部采用专用桥面板与横梁采用抱箍固定,横梁在纵桥向每隔75 cm布设1根,对应贝雷梁的竖杆或斜杆交叉点处设置。
在计算静力荷载时,仅计算主要构件的重量,包括桥面板、横梁、贝雷梁,忽略细部配件护栏的重量。

图5 贝雷梁布置
首先计算单个横梁传递给贝雷梁的集中荷载,将桥面板和横梁均转换成均布荷载,可利用结构力学求解器[15]求解横梁传递到桁架梁上的集中荷载,如图6所示。

图6 贝雷梁集中荷载计算
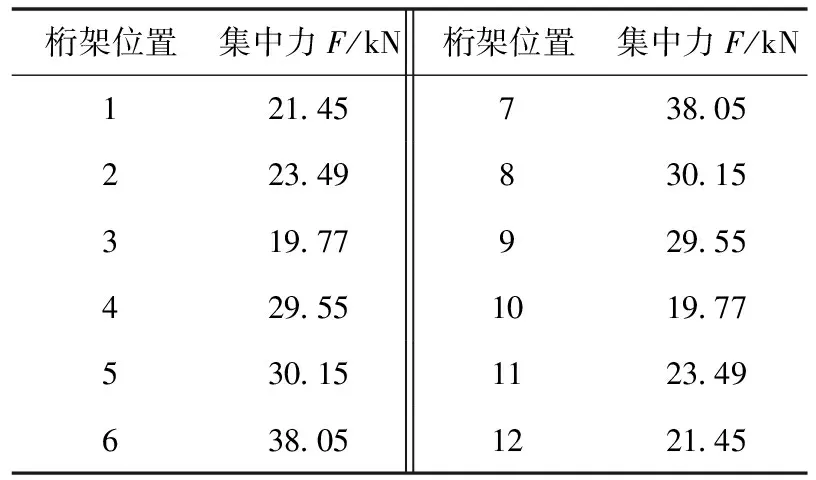
表4 贝雷梁集中荷载
将集中荷载叠加贝雷梁自重求出作用在桩顶梁上的集中荷载如表4所示。计算出集中荷载后加载于工况1桩顶梁和工况2桩顶梁上进行求解计算。
3.2 静力作用分析
将计算所得荷载加载于桩顶梁2上,进行有限元计算,图7为2种工况下位移云图对比,分析图7中数据可知,桩顶梁和钢管桩位移云图分布形状一致,桩顶梁2跨中位置竖向位移最大,梁端部竖向位移最小,原截面工况下最大竖向位移是1.604 mm,经简化后截面工况下最大竖向位移是1.613 mm,相差仅0.56%。图8为2种工况下米塞斯应力云图对比,分析图8中数据可知,桩顶梁和钢管桩应力云图分布形状一致,桩顶梁2和桩顶梁1接触处应力最大,梁端部和腹板中部应力最小,原截面工况下最大应力为14.7 MPa,经简化后截面工况下最大应力为14.8 MPa,相差仅0.68%;工况1计算结果文件所占内存43 MB,工况2计算结果文件所占内存26.5 MB,后者为前者的61.63%,由此可知,在上部结构静力荷载作用下,可用简化截面代替原截面进行静力计算,且简化后计算结果所占计算机内存较少。
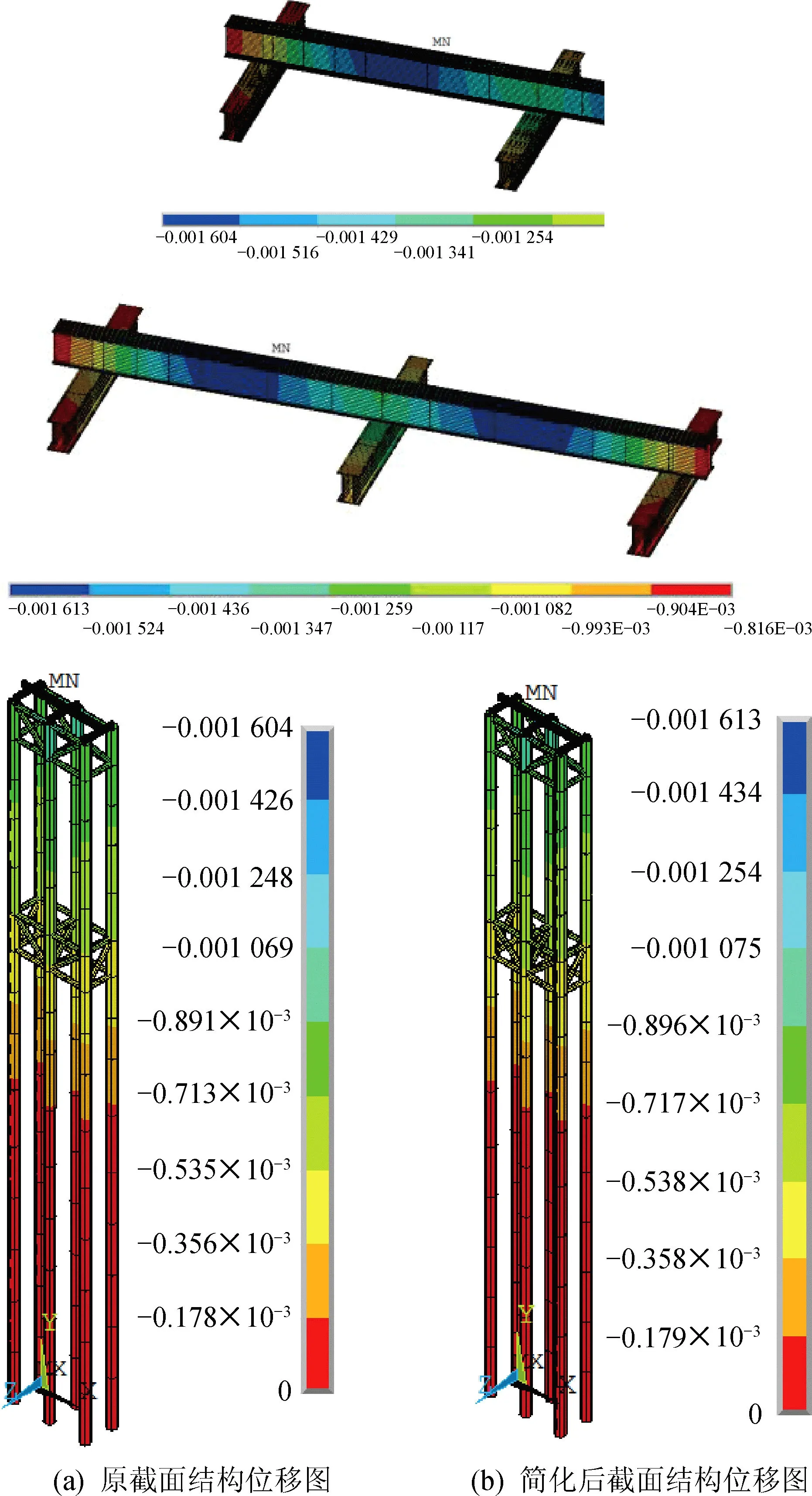
图7 2种工况下结构位移云图对比

图8 2种工况下结构应力图对比
4 动力作用分析
本文利用风荷载对2种截面进行动力响应分析。风荷载利用MATLAB编程,采用谐波叠加法进行拟合。
4.1 风荷载基本理论
4.1.1风速
从实测资料可知,风速可认为是长周期部分的平均风和短周期的脉动风叠加。因此,在实际工程应用中,可以将风对结构的作用看作是平均风和脉动风的叠加[15],即
v(x,y,z,t)=UZ2(z)+V(x,y,z,t),
(1)
平均风速沿高度变化的规律可用指数函数式近似表示为
(2)
式中:UZ1为高度Z1处的风速,m/s;UZ2为高度Z2处的风速,m/s;a为考虑地表粗糙度影响的无量纲幂指数。
脉动风可以由谐波叠加法求解。
4.1.2 谐波叠加法
谐波叠加法是基于三角级数求和的频谱表示法,采用以离散谱逼近目标随机过程模型的一种离散化数值模拟方法[16]。
将脉动风假定为一个一维、n变量、零均值的高斯随机过程{f(t)},其互谱密度矩阵为
(3)
对s0(w)进行Choleskey分解,即
s0(w)=H(w)HT*(w),
(4)
根据Shinozuka的理论,随机过程{f(t)}的样本可以由式(5)模拟:
cos(wmlt-θim(wml)+φml),
(5)

4.1.3 自相关功率谱
《公路桥梁抗风设计规范》中采用了考虑风速随高度变化的Kaimal谱,其简化形式可以表示为
(6)
(7)

sii(f)=Su(n),
(8)
其中,sii(f)为自相关功率谱。
4.1.4 互相关功率谱
脉动风的互相关功率谱为
(9)
ch(n)=e-λn|Z1-Z2|/UZ2,
(10)
式中:sii(f)为自相关功率谱;ch(f)为相关函数;λ为空间相关系数。
4.2 风荷载模拟
进行模拟横桥向风荷载作用下2种截面的动力响应差异,如图9所示。作用于桩顶梁上的风荷载主要由贝雷梁受风引起,因此,主要计算贝雷梁风荷载。贝雷梁距水面平均高度h=33.7 m,贝雷梁迎风面积8.194 m2,该地区多年平均风力4~6级,模拟时在此范围选取基本风速,本次模拟风速10 m/s,脉动风依据谐波叠加法基本原理,由MATLAB编程进行合成,如图10所示。

图9 风荷载作用图示意

图10 风速时程曲线
4.3 结果分析
风荷载加载时,由平均风速与脉动风速之和转换成风压时程曲线,再乘以受风面积转换成集中力时程曲线,以集中力时程曲线加载于受风贝雷梁和桩顶梁接触位置,如图9所示。2种工况经模拟计算后提取桩顶梁节点143的速度和加速度时程曲线,如图11所示。分析图9中数据可知,工况1中节点143最大速度绝对值为2.590 3×10-3m/s,工况2中节点143最大速度绝对值为2.590 9×10-3m/s,两者相差0.023%;工况1中节点143最大加速度绝对值为0.050 6 m/s2,工况2中节点143最大加速度绝对值为0.050 5 m/s2,两者相差0.2%。工况1计算动力计算时长为1 278 s,工况2计算动力计算时长为735 s,后者为前者的57.51%,工况1计算结果文件所占内存为9.57 GB,工况2计算结果文件所占内存为6.22 GB,后者为前者的64.99%,因此,在风荷载作用下,可用简化截面代替原截面进行动力响应分析,简化后计算时长更短,计算结果所占计算机内存更少。
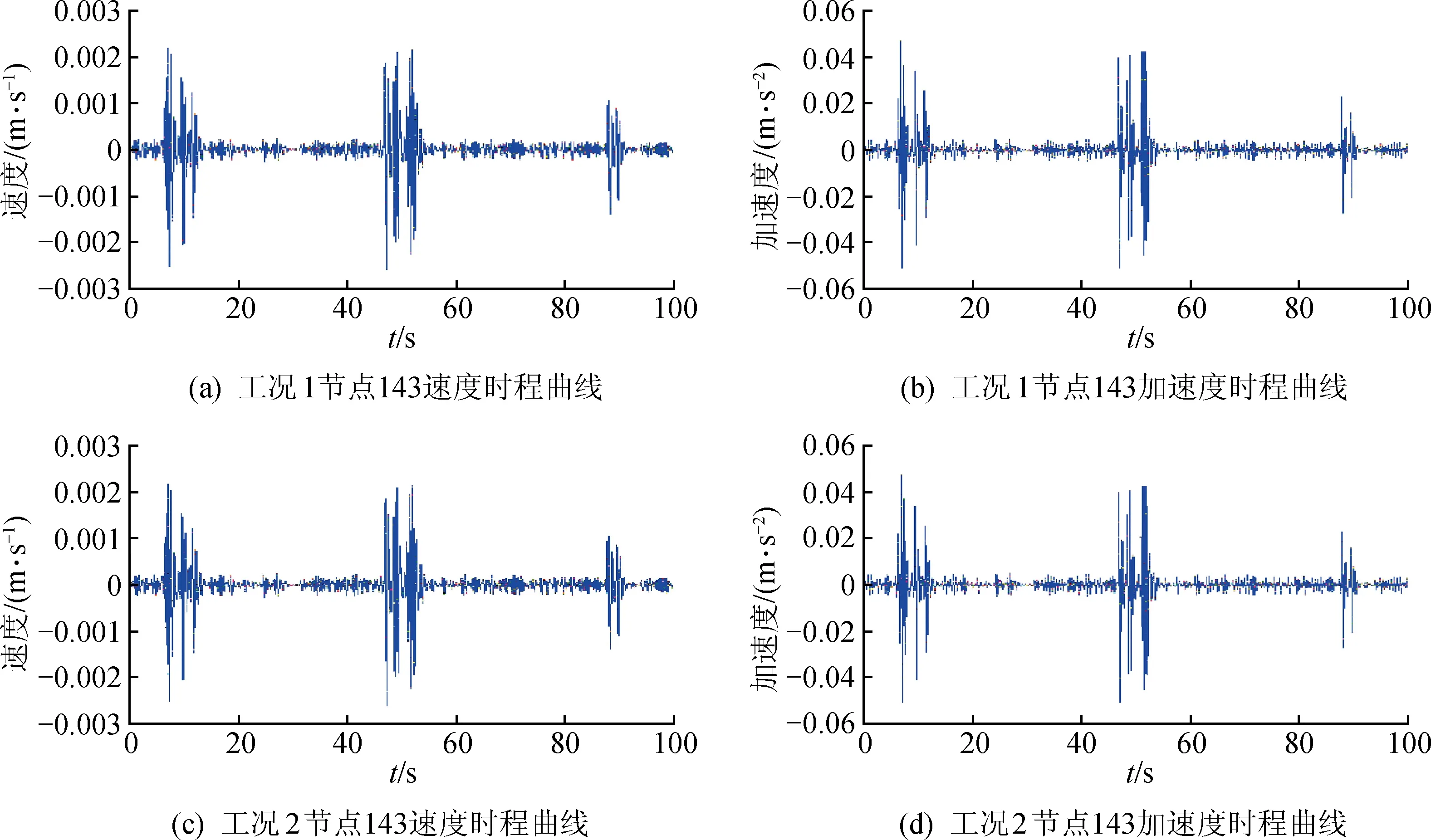
图11 2种工况下节点143速度、加速度时程曲线对比
5 结 语
通常采用有限元软件对钢栈桥进行受力分析时,钢栈桥桩顶梁和实际截面一致,采用工字钢截面形式,但该截面在有限元软件中建模复杂,本文将该截面进行简化,将其翼缘简化成矩形,然后进行静力和动力作用下的受力研究,并和原截面进行对比分析,结果表明:在上部结构静力荷载作用下,可用简化截面代替原截面进行静力计算;在风荷载作用下,也可用简化截面代替原截面进行动力响应分析;简化后计算结果接近,但计算时长更短,计算结果所占计算机内存更少,本文尚未研究车辆荷载作用下,两者之间的受力性能差异,车辆荷载既可作为静力加载,也可作为动力进行加载,可作为后续研究的方向。

