列车荷载作用下黄土阶梯斜坡的动力响应及稳定性研究

郑海忠，严武建, 2，石玉成, 2，卢玉霞, 2，王平, 2，李福秀

列车荷载作用下黄土阶梯斜坡的动力响应及稳定性研究

郑海忠1，严武建1, 2，石玉成1, 2，卢玉霞1, 2，王平1, 2，李福秀1

(1. 中国地震局兰州地震研究所 中国地震局(甘肃省)黄土地震工程重点实验室，甘肃 兰州 730000；2. 甘肃省岩土防灾工程技术研究中心甘肃 兰州 730000)

为研究黄土阶梯式斜坡的场地效应，选取宝兰客专通渭—秦安某路堤段阶梯式斜坡为研究对象进行现场测试和数值分析。对测试加速度时程从时域和频域2方面进行分析，研究不同列车对各阶梯田的振动特性的影响，研究结果表明：随着与轨道中心距离的增大，振动加速度峰值基本呈衰减趋势，但在第4阶梯田位置出现明显的振动反弹增大；各阶梯田处的加速度峰值和振动加速度级受到列车速度的影响，但由于振动放大区的存在，使得第3~5阶梯田处的加速度峰值在列车速度较小时，达到最大值；通过1/3倍频程分析，振动放大区主要对中心频率为1~10 Hz的成分进行放大。建立路基−地基−阶梯式斜坡模型，研究地基和各阶梯田土体弹性模量变化对振动的影响，发现在列车荷载和重力耦合作用下，使得各阶梯田边缘位置的最大位移和Mises应力大幅增大；地基土体弹性模量变化对各阶梯田处的振动都有明显的影响，而阶梯田土体弹性模量变化只对该阶和相邻前后2阶梯田的振动有影响，对远离该阶梯田处的振动基本无影响。

高速列车；梯田式斜坡；现场测试；数值计算；振动特性

铁路是国家的重要基础设施和民生工程，对社会和经济的发展有着非常重要的意义，特别是高速铁路的发展，使得人们的出行更加方便快捷但同时也带来了许多环境振动问题。根据我国铁路网建设的规划，到2020年我国高铁运行里程将达到3万km[1]。特别是近几年来高速铁路的发展，一方面使得人们出行更加便利、安全和舒适；另一方面使得环境振动问题日益突出。高速列车引起的环境振动与现场的土体性质、铁路断面形式、列车运行速度和列车编组等因素有着密切联系。因此，国内外许多学者对列车运行引起的环境振动进行了大量的实测和理论研究，这些研究表明高速列车引起的振动主要以竖向为主，且振动主要由列车运行速度、列车轴重以及轨道不平顺控制，轴重对振动的影响最为明显[2−4]。通过现场实测和理论研究发现，高速列车荷载作用下产生的地面振动随着距离而衰减，但在一定距离范围内，会存在一个振动放大区，产生这种现场的主要原因是列车运行速度接近土体Rayleigh波速[5−11]。同时，已有学者研究了土体力学参数对列车振动的影响，发现土体的弹性模量对振动的影响最为敏感[12]。以上研究主要集中在列车以及土体力学参数对环境振动的影响，且这些研究主要集中在饱和软土地区。铁路沿线存在着大量复杂的地形地貌，高速列车通过时，不同的地形地貌其动力响应是不同的。而宝兰客运专线为我国“八横八纵”高速客运网的重要部分，该线路约3/4处在天礼盆地，沿线分布着大量的黄土梁、峁、沟壑和丘陵，且地形地质条件复杂，湿陷性黄土层厚度大、等级高[13]。在地震工程中不同地形地貌在地震作用下的场地效应已有研究，石玉成等[14−15]利用爆破震源研究了黄土斜坡场地的振动传播特性，发现斜坡场地对振动有明显的放大作用。刘晶波[16]研究了局部凸起地形对地震传播的影响，得出在局部凸起地形上面会使得地震动放大。然而关于列车通过时不同地形地貌的振动特性研究较为空白。因此，本文为研究在列车荷载作用下黄土地区典型地形地貌的振动特性，选取宝兰客专沿线通渭—秦安某路堤段的阶梯式斜坡为研究对象，测试了列车以不同编组和速度经过该处时引起的振动。基于现场概况建立有限元数值模型，研究该阶梯式斜坡土体力学参数对振动传播的影响。开展高速列车荷载作用下湿陷性黄土地区的地形地貌对振动传播特性的研究，对于我国黄土地区铁路工程的定性预测、新建设计以及列车的安全运行具有重要的科学意义。

1 现场测试方案

1.1 现场概况及测点布置

试验工点位于宝兰高铁秦安—通渭段，该段测试为高速铁路路堤，沿线路一侧场地地势平坦开阔；另一侧为阶梯状斜坡，共有5个阶梯，是典型的黄土梯田，梯田土层主要是素填土和粉质黄土，每阶梯田地势宽阔平坦，布置测点方便容易。每阶梯田的几何尺寸为：第1阶梯田的前段边缘距轨道中心14 m，其前端坡面长为1.4 m，坡角为80°，梯田长为7.5 m；第2阶梯田高出第1阶3 m，长度为5.4 m；第3阶梯田高第2阶为2.6 m，长度为7.4 m；第4阶梯田距第3阶为2.5 m，长度为8.4 m；第5阶梯田距第4阶为3.3 m，且第5阶梯田场地广阔地势平坦。为了对比研究振动在每一阶梯田的传播特性，依次在每阶梯田边缘布置测点，如图1所示。

1.2 测试仪器及车辆特征

测试仪器采用891-Ⅱ型测振仪，其由中国地震局工程力学研究所研制，加速度测试范围为0~2.0，采样间隔为0.005 s，该仪器的记录长度为激震前5 s，激震后35 s。在本次测试中规定方向为列车运行的方向，方向垂直于线路方向，方向为重力方向。

现场共采集到了10列动车数据，为了研究列车运行速度对各阶梯田振动的影响，从中选取型号相同为CRH2C，运行方向相同，编组相同，但运行速度不同的3列动车数据作为研究对象，这保证了振源的一致性。利用速度测试仪测试了每列动车经过该测段的速度，按照车速大小依次编号为1~3号。各列车相关参数如表1所示。

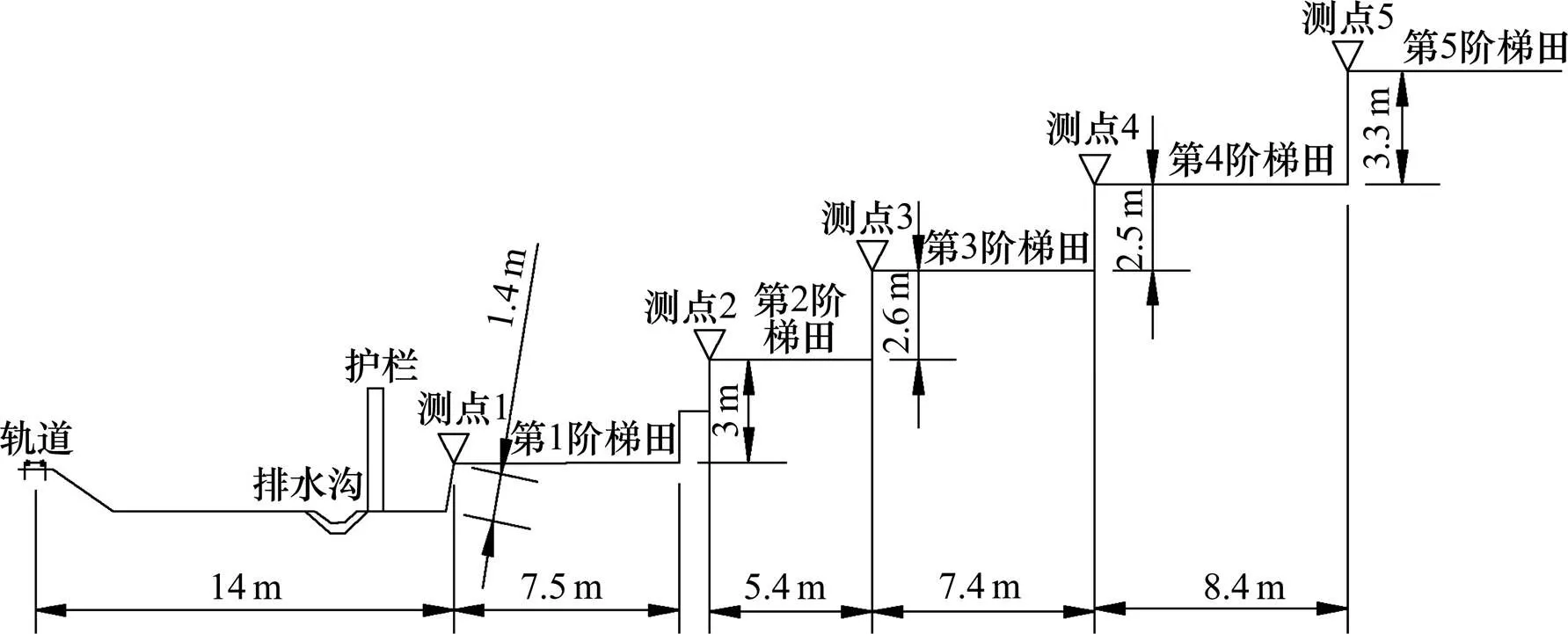
图1 测点布置示意图

表1 测振仪记录的3个车次基本参数

2 测试结果分析

2.1 振动加速度时程响应分析

现场对以上3组列车通过该测试段的加速度时程均有记录，图2是以1号列车通过时为例，不同测点竖直方向的加速度时程曲线。

从图中可以看出，列车经过时各个测点的振幅强度明显增大，要强于无列车经过时2个数量级。各个测点的振动持时基本一致，大约为3.5 s。测点1的加速度时程曲线具有明显的正负对称性，且正向和负向的加速度峰值基本一致，这与其他测点明显不同。在列车经过时，5个测点的振动加速度峰值为：16.02，11.44，11.68，13.55和7.90 cm/s，随着距轨道中心越远，加速度基本呈现衰减趋势，但在测点4加速度峰值反弹增大，这主要是由于振动波传播到各阶梯田边界位置时会发生折射和反射作用，折射波、反射波以及直达波叠加所造成的；此外，在振动波传播的过程中，其波速会与土体的瑞利波速相近，使得土体发生共振，使得测点4的加速度峰值出现反弹。

2.2 列车速度对振动传播的影响

列车荷载作用下产生的振动加速度大小是引起路基沉降、边坡失稳以及轨道变形的主要因素。同时，列车运行引起的振动，对人们的生活和学习环境产生了重要影响，其影响大小主要由振动加速级来评价[17]。因此，从振动加速度峰值max和振动加速级VAL(dB)两方面来分析列车运行速度对各阶梯田振动的影响。

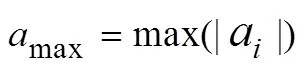
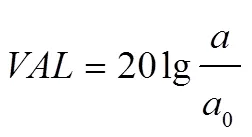
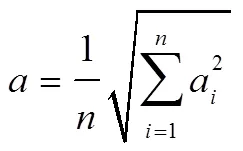
式中：i为第个采样点的加速度；为振动加速度有效值，m/s2；0为振动基准加速度有效值，10−6m/s2；为采样点个数。

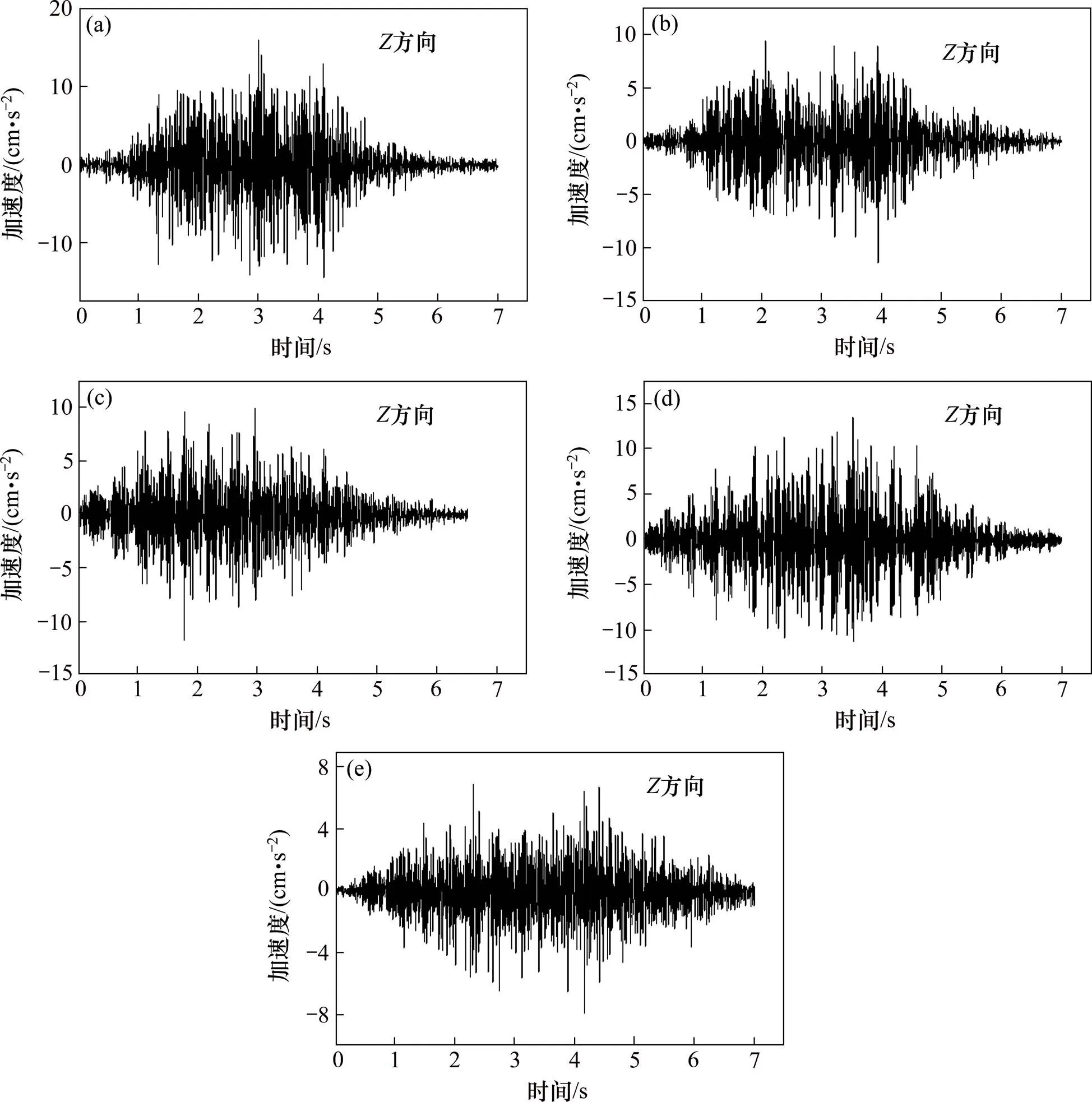
(a) 测点1；(b) 测点2；(c) 测点3；(d) 测点4；(e) 测点5

由式(1)~(2)可以计算得到列车以不同速度经过时引起的加速度峰值和振动加速度级，如图3所示。可以看出，不同速度列车引起的加速度峰值和振动加速度级的变化规律基本一致，距轨道中心越远，其并不是呈单调衰减，在第4阶梯田边缘位置出现了加速度和振动加速度级反弹增大的现象。在第1阶梯田，加速度峰值和振动加速度级与速度的大小成正比；在第2阶梯田，加速度峰值与列车速度不成正比，但振动加速度级依然和速度成正比，时速214 km/h的1号列车引起的加速度峰值要大于时速220 km/h的2号列车；在第3阶梯田，加速度峰值和振动加速度级都与列车速度不成正比，且时速214 km/h的1号列车引起的振动出现了反弹增大现象，且其达到了最大值；在第4阶梯田，不同速度列车引起的加速度和振动加速度级都呈现出反弹增大的现象，时速214 km/h的1号列车引起的加速度峰值最大，而振动加速度级却小于时速242 km/h的3号列车；在第5阶梯田，加速度峰值和振动加速度级与速度的大小成正比，且不同速度列车引起的加速度峰值相差不大，但振动加速度级却变化较大。表明出现“振动反弹”的位置与车速的大小有明显关系，且场地振动的强度不仅受到列车速度的控制，而且还与场地地形地貌特征有密切关系，甚至场地条件的影响要大于列车速度的影响。

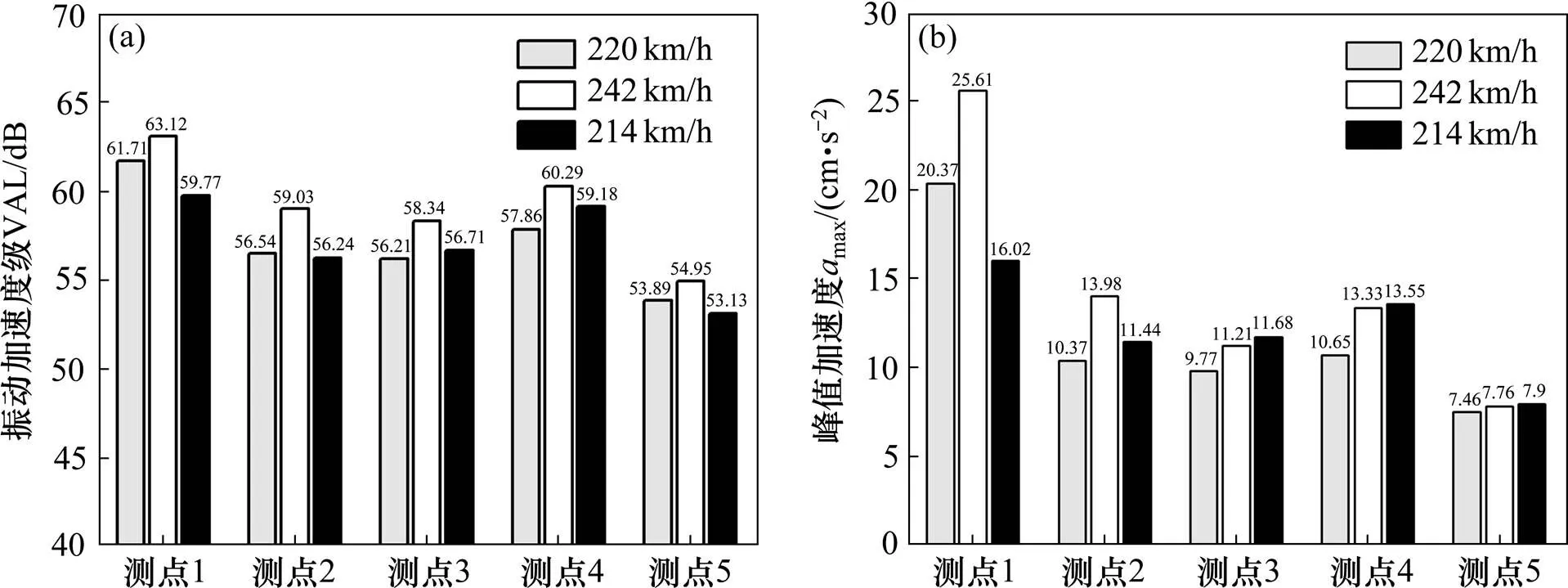
(a) 加速度峰值；(b) 振动加速度级

2.3 加速度信号的1/3倍频程分析

在对振动信号做频域分析时，一般不需要对每个频率值逐个分析，而是把振动信号的频率范围划分成若干频带，测量和计算在这些频带上的加速度级。频带中高的截断频率和低截断频率分别记作f和f，其倍频程定义为[18]：

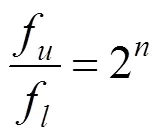
在噪声和振动测试分析中，常取=1/3，并称其为1/3倍频程。各频程用其中心频率f来表示，其表达式为：

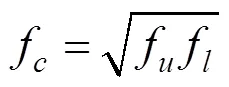
通过对各梯田的振动信号进行1/3倍频程分析，可以清晰地看到各个频带中振动变化情况，如图4。从图4中可以看出，测点5在中心频率为1~6.3 Hz频带内的振动相对于测点1的振动出现了明显的反弹增大现象，测点4在中心频率为1~1.6，3.15~6.3和31.5~50 Hz内的振动相对于测点1的振动出现了反弹增大现象，测点3在中心频率为5~6.3 Hz和20 Hz内的振动相对测点1的振动出现了振动反弹增大。可以看出，随着距离轨道中心越远，各测点的高频振动都发生了衰减，但第4和第5阶梯田使得低频范围内的振动呈现出放大现象。

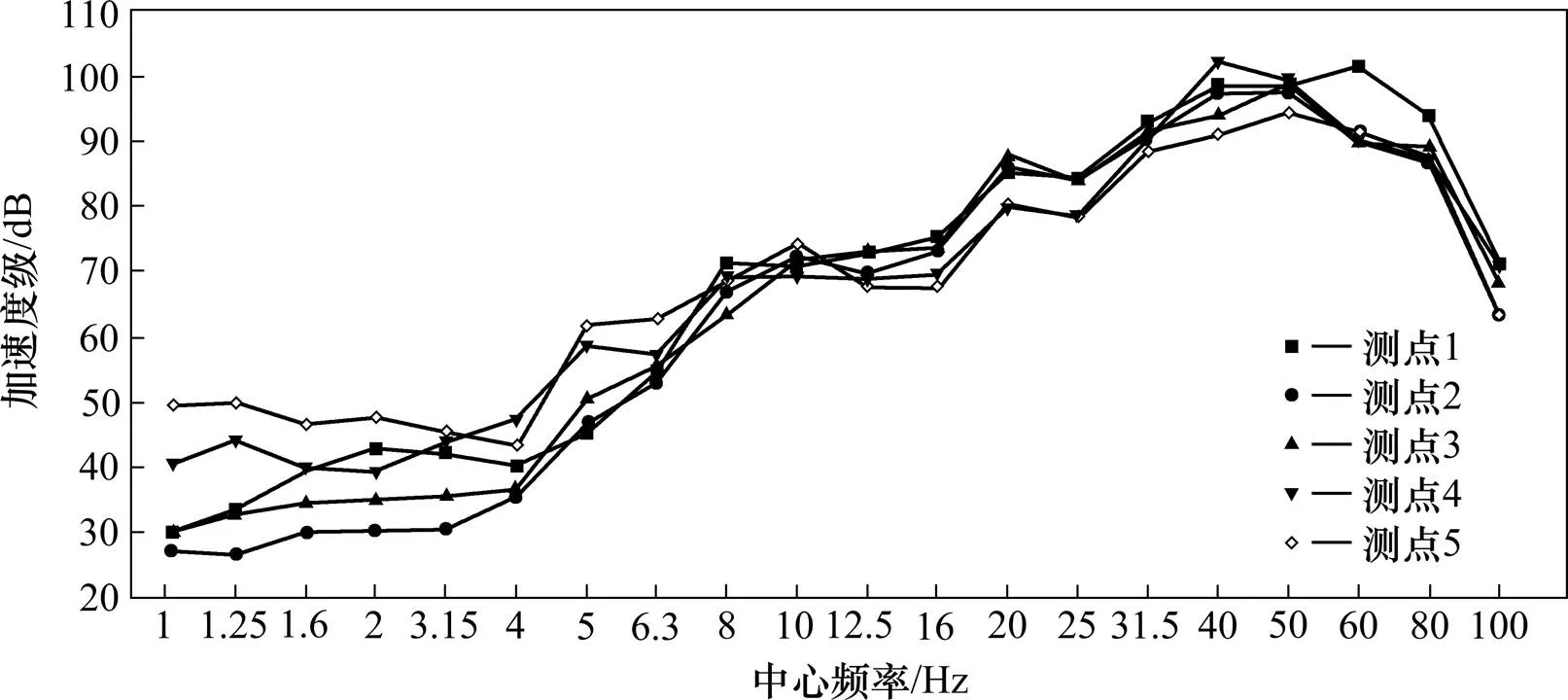
图4 1号列车通过时各测点的1/3倍频程曲线

3 振动数值计算分析

根据现场测试概况，利用有限元数值软件ABAQUS建立对应的阶梯式斜坡有限元模型，进一步科学地计算和评估高速列车荷载作用下梯田式斜坡的振动特征。

3.1 数值计算模型

列车在轨道上运行所产生的激振力可以表 示为[19]：

()=0+1sin(1)+2sin(2)+3sin(3) (6)

式中：0为轮轴静载，取0=80 kN；1为行车不平顺产生的振动荷载；2为列车运行作用到线路上的动力附加荷载；3为波形磨耗振动荷载，其中p的表达式为：

p=0αω2(=1, 2, 3) (7)

式中：0为列车簧下质量，取0=750 kg；α为典型矢高；ω为由轨道不平顺引起的列车以不同速度运行时产生的振动频率，其表达式为：

ω=2π/L(=1, 2, 3) (8)

式中：为列车的速度；L为典型波长，其中典型的不平顺振动波长和相应的矢高采用英国铁路轨道不平顺功率谱，1=10 m，1=3.5 mm；2=2 m，2=0.4 mm；3=0.5 m，3=0.08 mm。

在列车荷载作用范围内，将作用在路基上的荷载等效为沿线路纵向均匀分布的荷载ave()为：

ave()=()/(9)

式中：为修正系数；为每节车厢的轮对数；为列车车厢编组；为列车长度。

当列车运行速度为242 km/h时，其产生的荷载如图5所示。

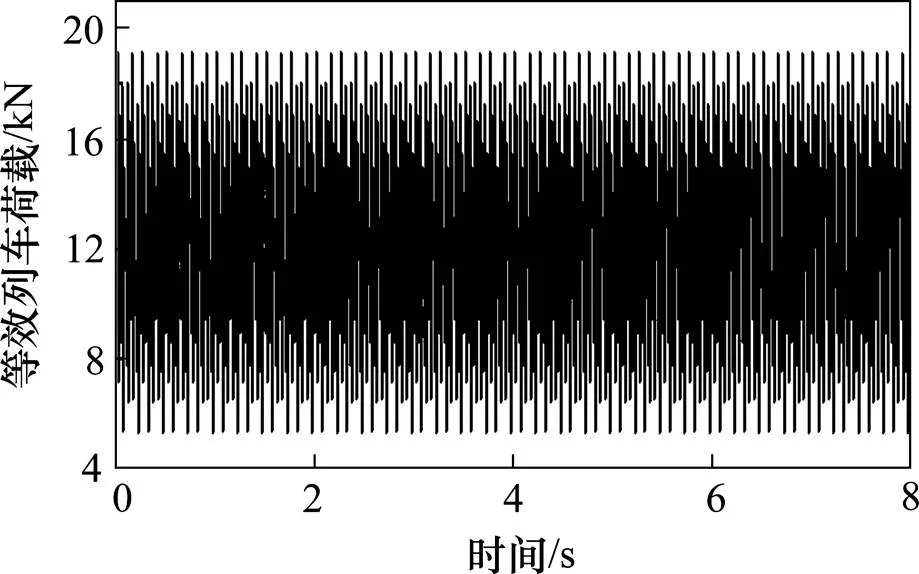
图5 速度242 km/h的竖向列车荷载

根据现场实测概况、高速铁路设计要求及相关研究[20]，建立相应的二维数值计算模型，如图9所示。模型分为2部分，第1部分为路基，从上到下依次为0.4 m的基床表层、2.3 m的基床底层、3.6 m的路基基础；第2部分为地基和各阶梯田式斜坡。模型左右边界和底部为了防止波的反射作用，均采用无限元边界，路基材料力学参数和土体力学参数如表2所示。

表2 路基及土体参数

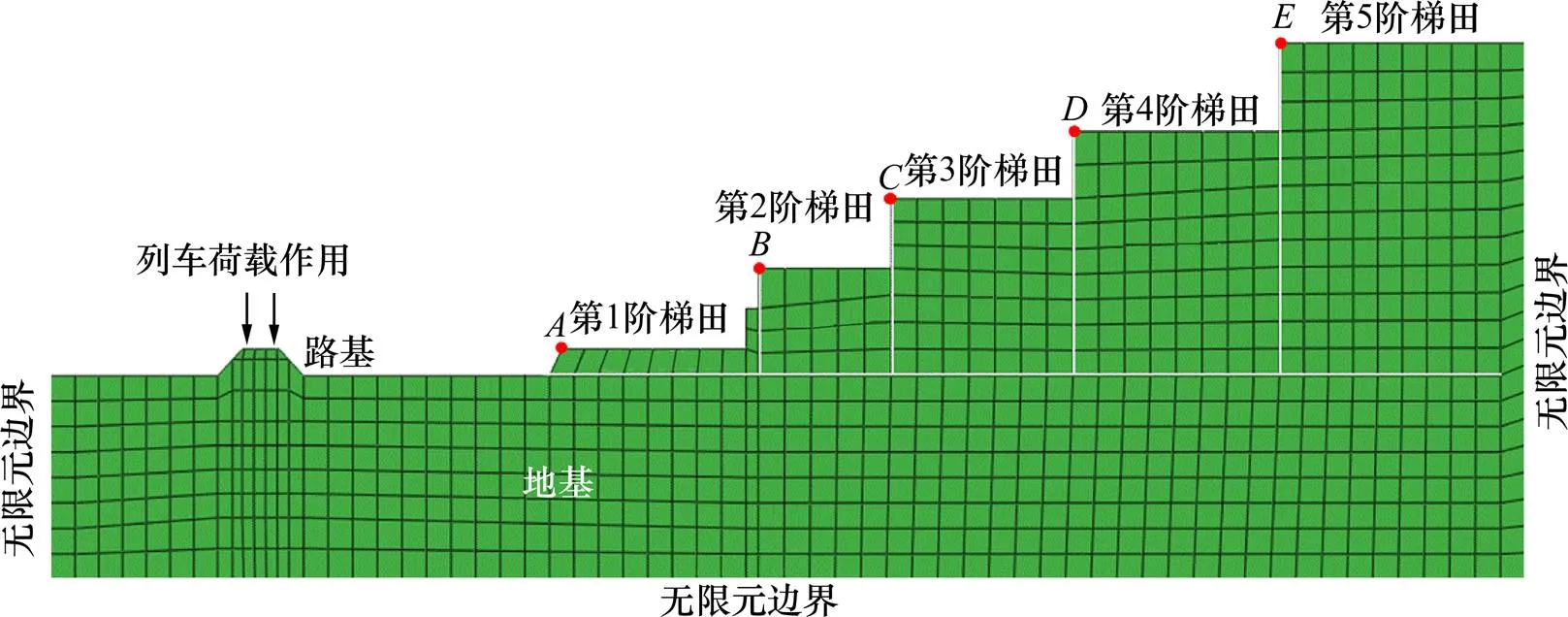
图6 有限元数值模型

3.2 数值计算结果

3.2.1 斜坡稳定性分析

在天然状态下斜坡稳定性主要受到重力作用的影响，然而铁路沿线的斜坡不仅受到重力的作用，同时受到列车荷载的周期性作用。为了研究列车荷载作用下阶梯斜坡的稳定性，对比了仅受重力荷载和受重力及列车荷载耦合作用下斜坡的最大位移云图和Mises应力云图，如图7~8所示。

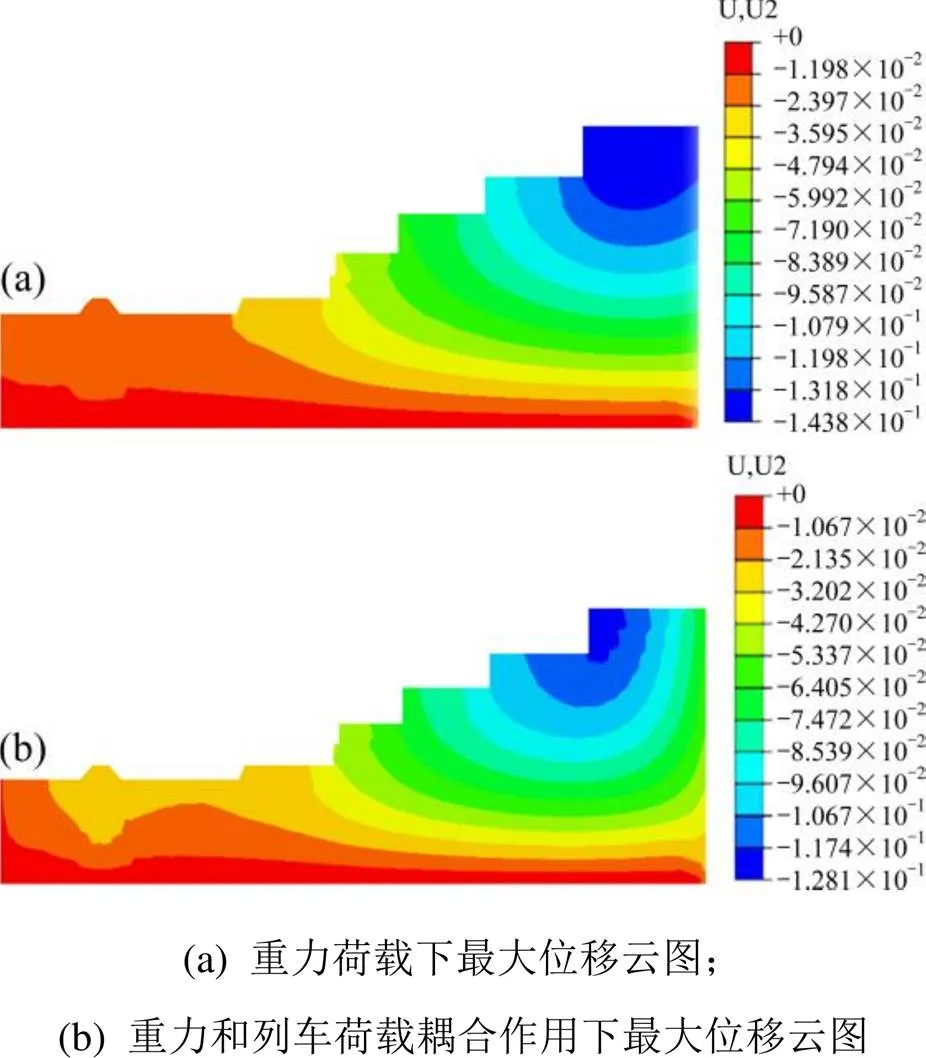
图7 最大位移云图对比

从图7可以看出，相比于重力荷载下的位移云图，列车荷载作用使得最大位移云图明显发生了变化。列车荷载作用下使得路基下方的位移明显增大，同时使得各阶梯田前边缘处的位移增大，尤其是第5阶梯田处，其右侧的沉降位移量明显增加。由此可知，列车荷载作用下使得阶梯斜坡每阶边缘位置的位移变大，其为振动敏感区域。从图8可知，列车荷载的作用使得斜坡的Mises应力明显增大，且改变了其云图分布。列车荷载的作用使得路基下方的Mises应力明显增大，同时使得每阶梯田下方的同一Mises应力的分布范围扩大。特别是在第5阶梯田处，Mises应力增大的范围一直延续到了地基内部。

因此，在列车荷载作用下，要特别注意阶梯田边缘位置失稳破坏，在斜坡加固时要特别考虑阶梯田的边缘位置。

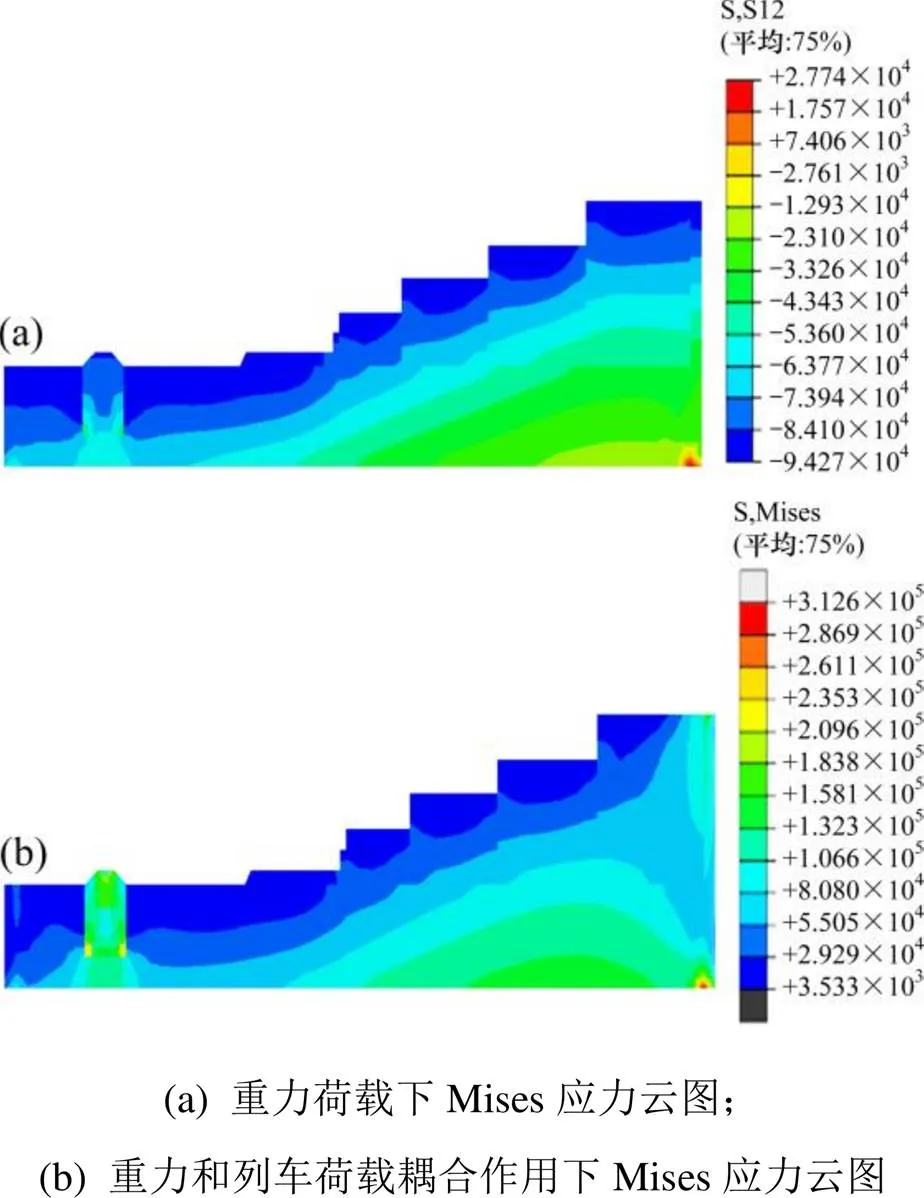
图8 Mises应力云图对比

3.2.2 振动传播特性分析

由于振动波的传播主要受到场地波速和厚度的影响，而场地波速的大小直接与场地的弹性模量有关[21]。鉴于此，本文建立地基和各阶梯田在不同弹性模量下的数值模型，以分析地基和各阶梯田土体波速对振动传播的影响作用。

因此，分别选择土体弹性模量为15，45，75和105 MPa来分析地基和各阶梯田土体弹性模量变化对振动传播的影响。分别在各阶梯田边缘布置测点~，对比各个测点的地面振动加速度峰值，计算结果如图9所示。

从图9可以看出，当地基、第1~4阶梯田土体弹性模量为15 MPa和第5阶梯田弹性模量为45 MPa时，振动加速度峰值的变化规律及数值与实测结果基本一致，说明所建数值模型的正确性及可行性(图9(f))。地基和不同阶梯田土体弹性模量变化对振动传播有不同的影响，其振动加速度出现反弹增大的位置与场地条件有密切关系。

由图9(a)可知，当地基弹性模量为15 MPa时，垂直方向的振动加速度峰值随着距轨道中心距离的增加而衰减，在每一阶梯田边缘位置都未呈现出放大现象，且随着弹性模量的增加，测点，，和的垂直方向振动加速度峰值减小，而测点的垂向振动加速度峰值在一定范围内随着地基弹性模量的增加而增加，其反弹现象越明显。

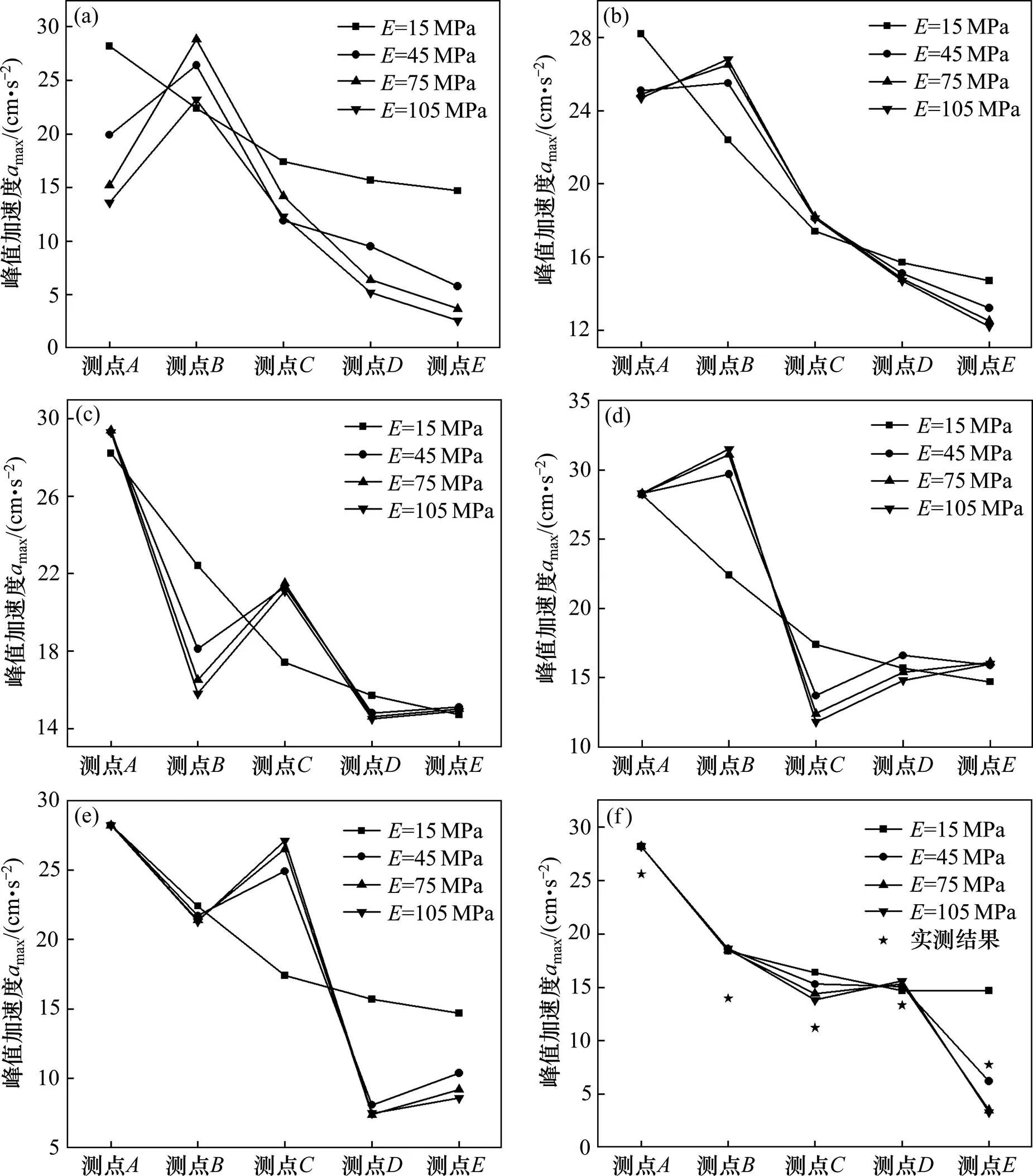
(a) 地基弹性模量变化；(b) 第1阶梯田弹性模量变化；(c) 第2阶梯田弹性模量变化；(d) 第3阶梯田弹性模量变化；(e) 第4阶梯田弹性模量变化；(f) 第5阶梯田弹性模量变化

从图9(b)可以看出，测点，和的垂向振动加速度峰值随着第1阶梯田土体弹性模量的增大而减小，测点垂向振动加速度峰值随弹性模量的增大而增大，且在测点的垂向振动加速度峰值反弹越明显，对测点的垂向振动加速度峰值影响 较小。

由图9(c)可知，测点和的垂向振动加速度峰值随着弹性模量的增加而逐渐减小，测点，和的垂向振动加速度峰值随弹性模量的增大而增大，且在测点和垂向振动加速度峰值出现了明显的反弹。

由图9(d)可知，弹性模量变化对测点的垂向振动加速度峰值基本没有影响，测点和的垂向加速度峰值随弹性模量的增加而增大，测点和的加速度峰值随弹性模量的增大而减小，且随着弹性模量的增加在测点和垂向加速度峰值都出现了反弹现象。

由图9(e)可知，测点，和的垂向加速度峰值随弹性模量的增加而减小，测点的垂向加速度峰值随着弹性的增加而增加，且随着弹性模量的增加测点和的垂向加速度峰值出现了明显的放大现象，但测点的加速度峰值基本不受弹性模量变化的影响。

由图9(f)可知，弹性模量变化对测点和的垂向加速度峰值基本没有影响。测点和的垂向加速度峰值随弹性模量的增加而减小，且随着弹性模量的增加，测点的垂向加速度峰值反弹现象越明显。

由上述分析可知，地基土体弹性模量变化对各阶梯田的垂向振动有较大的影响，随着地基土体弹性模量的增加使得测点的垂向加速度峰值出现明显的放大。阶梯田土体弹性模量变化对相邻两梯田边缘处的垂向振动加速度峰值影响明显，随着该阶梯田弹性模量的增加，使得该阶梯田边缘的垂直振动加速度峰值快速减小，使得前一阶梯田和后一阶梯田边缘处的垂向振动加速度峰值增大，对远离该梯田处的振动加速度峰值基本无影响。

4 结论

1) 在列车荷载作用下，路堤段阶梯式斜坡各阶梯田边缘处的振动加速度峰值基本随距轨道中心距离增加呈衰减趋势，但在第4阶梯田振动出现了明显的反弹增大。

2) 列车运行引起的振动加速度峰值和振动加速度级受到列车速度的影响，在距轨道中心较近的前2阶梯田处的振动加速度峰值随列车运行速度的提高而增大，但后3阶梯田处，由于振动反弹的存在，使得速度较小的1号列车引起的加速度峰值最大。

3) 通过对测试加速度时程进行1/3倍频程分析的结果表明，第4和第5阶梯田对振动的放大作用主要集中在中心频率1~10 Hz内，而在中心频率大于10 Hz时，加速度级随与轨道中心距离的增大而减小。

4) 在列车荷载与重力耦合作用下，每阶梯田边缘的最大位移和Mises应力都明显的增大。因此，铁路沿线斜坡防治要特别注意其边缘位置的加固。

5) 地基土体弹性模量增加使得测点垂直方向的振动加速度峰值增大，出现了明显的放大现象，但其他测点的加速度峰值随之减小；阶梯田土体弹性模量增大，使得该梯田边缘处的振动加速度峰值减小，使得前一阶和后一阶梯田边缘处的垂直方向振动加速度峰值增加，对远离该阶的测点基本无影响。

[1] 翟婉明, 赵春发. 现代轨道交通工程科技前沿与挑战[J]. 西南交通大学学报, 2016, 51(2): 209−226. ZHAI Wanming, ZHAO Chunfa. Frontiers and challenges of sciences and technologies in modern railway engineering[J]. Journal of Southwest Jiaotong University, 2016, 51(2): 209−226.

[2] 高广运, 李志毅, 冯世进, 等. 秦−沈铁路列车运行引起的地面振动实测与分析[J]. 岩土力学, 2007, 28(9): 1817−1822. GAO Guangyun, LI Zhiyi, FENG Shijin, et al. Experimental results and numerical predictions of ground vibration induced by high-speed train running on Qin-Shen railway[J]. Rock and Soil Mechanics, 2007, 28(9): 1817−1822.

[3] 郑晓, 刘胜群. 地铁运行引起地表振动的现场测试与分析[J]. 铁道建筑, 2007(6): 41−43. ZHENG Xiao, LIU Shengqun. Field test and analysis of surface vibration caused by subway operation[J]. Railway Engineering, 2007(6): 41−43.

[4] 孟祥连, 周福军. 西宝高铁黄土地区路基振动效应空间分析研究[J]. 铁道工程学报, 2017, 34(8): 28−33. MENG Xianglian, ZHOU Fujun. Spatial analysis and study of roadbed vibration effect on loess area for Xi’an Baoji high speed railway[J]. Journal of Railway Engineering Society, 2017, 34(8): 28−33.

[5] 屈畅姿, 王永和, 魏丽敏, 等. 武广高速铁路路基振动现场测试与分析[J]. 岩土力学, 2012, 33(5): 1451− 1456. QU Changzi, WANG Yonghe, WEI Limin, et al. Field test and analysis of roadbed vibration of Wuhan-Guangzhou high speed railway[J]. Rock and Soil Mechanics, 2012, 33(5): 1451−1456.

[6] 马骙骙, 李斌, 王东, 等. 宝兰客专路堤段地面振动特性试验研究与数值分析[J]. 铁道科学与工程学报, 2019, 16(2): 294−301. MA Kuikui, LI Bin, WANG Dong, et al. Experimental study and numerical analysis on ground vibration characteristics of subgrades section of Baoji-Lanzhou high-speed railway[J]. Journal of Railway Science and Engineering, 2019, 16(2): 294−301.

[7] 董连成, 徐禛, 师黎静, 等. 多年冻土区青藏铁路列车荷载作用下路基振动响应研究[J]. 地震工程学报, 2018, 40(6):1153−1160. DONG Liancheng, XU Zhen, SHI Nijing, et al. Vibration response analysis of embankments in permafrost regions along the Qinghai—Tibet railway subjected to train loads[J]. China Earthquake Engineering Journal, 2018, 40(6): 1153−1160.

[8] 王子玉, 凌贤长, 惠舒清. 季节冻土区铁路路基振动加速度现场监测[J]. 岩土工程学报, 2015, 37(9): 1591− 1598. WANG Ziyu, LING Xianchang, HUI Shuqing, et al. Field monitoring of vibration response of subgrade in a seasonally frozen region[J]. Chinese Journal of Geotechnical Engineering, 2015, 37(9): 1591−1598.

[9] 陈功奇. 基于现场测试的列车引起地基振动分析[J]. 岩石力学与工程学报, 2015, 34(3): 601−611. CHEN Gongqi. Ground vibration analysis induced by high-speed train based on in-situ data[J]. Chinese Journal of Rock Mechanics and Engineering, 2015, 34(3): 601− 611.

[10] SHENG X, Jones C J C, Thompson D J. A theoretical study on the influence of the track on train-induced ground vibration[J]. Journal of Sound & Vibration, 2004, 272(3): 909−936.

[11] SHENG X, Jones C J C, Thompson D J. A theoretical model for ground vibration from trains generated by vertical track irregularities[J]. Journal of Sound & Vibration, 2004, 272(3): 937−965.

[12] 张光明. 高速铁路路基段地面振动响应研究[D]. 成都: 西南交通大学, 2014. ZHANG Guangming. Study on the ground vibration induced by trains moving on subgrade of hig speed railway[D]. Chengdu: Southwest Jiaotong University, 2014.

[13] 付伟. 宝兰客运专线湿陷性黄土分布规律及地基处理技术分析[J]. 铁道标准设计, 2014, 58(11): 15−19. FU Wei. Distribution rules of collapsible loess and analysis on foundation treatment technology on Baoji- Lanzhou passenger dedicated line[J]. Railway Standard Design, 2014, 58(11): 15−19.

[14] 石玉成, 王兰民, 林学文. 黄土场地的爆破地震振动效应[J]. 岩石力学与工程学报, 2003, 22(11): 1933−1938. SHI Yucheng, WANG Lanmin, LIN Xuewen. Blasting vibration effect of loess site[J]. Chinese Journal of Rock Mechanics and Engineering, 2003, 22(11): 1933−1938.

[15] 石玉成, 卢育霞, 何少林, 等. 爆破震动作用下斜坡体的地震动分布及其动应力响应特征[J]. 岩石力学与工程学报, 2014, 33(增2): 3707−3717. SHI Yucheng, LU Yuxia, HE Shaolin, et al. Seismic distribution and dynamic stress response characteristics of slope body under blasting vibration[J]. Chinese Journal of Rock Mechanics and Engineering, 2014, 33(Suppl 2): 3707−3717.

[16] 刘晶波. 局部不规则地形对地震地面运动的影响[J]. 地震学报, 1996, 18(2): 239−245. LIU Jingbo. Effect of locally irregular topography on earthquake ground motion[J]. Acta Seismologica Sinica, 1996, 18(2): 239−245.

[17] GB 10071—1988, 城市区域环境振动测量方法[S]. GB 1007—1988, Measurement method of environment vibration of urban area[S].

[18] 毛东兴, 洪宗辉. 环境噪声控制工程[M]. 2版.北京: 高等教育出版社, 2010: 16−18. MAO Dongxing, HONG Zonghui. Environmental noise control engineering[M]. 2nded. Beijing: Higher Education Press, 2010: 16−18.

[19] 梁波, 罗红, 孙常新. 高速铁路振动荷载的模拟研究[J]. 铁道学报, 2006, 28(4): 89−94. LIANG Bo, LUO Hong, SUN Changxin. Simulation of vibration load on high speed railway[J]. Journal of the China Railway Society, 2006, 28(4): 89−94.

[20] 罗晶. 兰州黄土地区高速铁路路堤地段环境振动研究[D]. 兰州: 兰州交通大学, 2016. LUO Jing. Study on environmental vibration of high- speed railway embankment section in Lanzhou loess area[D]. Lanzhou: Lanzhou Jiaotong University, 2016.

[21] 廖振鹏. 工程波动理论导论[M]. 2 版. 北京: 科学出版社, 2002: 190−227. LIAO Zhenpeng. Introduction to wave motion theories in engineering[M]. 2nd ed. Beijing: Science Press, 2002: 190−227.

Study on dynamic response and stability of loess stepped slope under train load

ZHENG Haizhong1, YAN Wujian1, 2, SHI Yucheng1, 2, LU Yuxia1, 2, WANG Ping1, 2, LI Fuxiu1

(1. Key Laboratory of Loess Earthquake Engineering, Lanzhou Institute of Seismology, CEA, Lanzhou 730000, China; 2. Geotechnical Disaster Prevention Engineering Technology Research Center of Gansu Province, Lanzhou 730000, China)

In order to study the site effect of stepped loess slope, field test and numerical analysis were carried out on a stepped slope of Tongwei-Qin’an embankment section of Baoji-Lanzhou high-speed railway. The time history of acceleration was analyzed in both time and frequency domains, and the effects of different trains on the vibration characteristics of different terraces were studied. The results show that with the increase of the distance from the track center, the peak acceleration tends to attenuate. There is an obvious vibration rebound at the fourth terrace. The peak acceleration and vibration acceleration level of each step field are affected by train speed. However, due to the existence of vibration amplification zone, the peak acceleration of the third to fifth step field reaches its maximum when the train speed is small. Through 1/3 octave frequency analysis, the vibration amplification region mainly amplifies the components of the central frequency from 1 Hz to 10 Hz. A model of subgrade-foundation-stepped slope is established to study the influence of the change of elastic modulus of soil on vibration. It is found that coupling action of train load and gravity, the maximum displacement and Mises stress at the edge of each terrace field increase greatly. And the change of elastic modulus of soil has obvious influence on the vibration of stepped fields, while the change of elastic modulus of soil in stepped fields only affects the vibration of the stepped fields and the two adjacent stepped fields. It has no effect on the vibration far away from the terrace.

high speed train; terraced slope; field test; numerical calculation; vibration characteristics

TU444

A

1672 − 7029(2020)05 − 1080 − 10

10.19713/j.cnki.43−1423/u.T20190796

2019−09−07

国家重点研发计划课题资助项目(2017YFC1500906)；中国地震局地震预测研究所基本科研业务费专项资助项目(2014IESLZ01)；国家自然科学基金面上资助项目(51678545，41472297)

严武建(1980−)，男，江西鹰潭人，副研究员，博士，从事岩土地震工程及混凝土耐久性研究；E−mail：yanwj1980@126.com

(编辑 蒋学东)