差压式浓硫酸液位和密度检测系统的研究

王向飞，张辽远，杨 光，张百慧，慕 丽

(沈阳理工大学 机械工程学院，沈阳 110159)

在大力提倡节能环保的情况下，电能逐步取代传统石油、煤炭等不可再生资源。电池行业得到迅猛发展，各种新型电池不断被研制和应用，铅蓄电池凭借蓄电能力强、使用寿命长、可多次循环利用、价格便宜等优势被广泛应用于生产生活中，也被作为轮船、军舰的主要动力来源。蓄电池中电解液的液位[1]和密度[2]直接决定电池的性能，因此，精准测量[3]电解液的液位和密度可以有效监测电池质量，对电池起到保护作用。

对比分析多种形式的密度和液位测量方式发现：人工检尺法可作为现场快速测量液体液位的测量手段，但读取刻度线的方式会产生较大的误差；浮子式液位计可测量储罐的液位和密度，但液位垂直方向的涌动对测量结果影响较大，造成严重的测量误差；一些利用声、光、射线等能量的非接触式[4]液位测量方式成本较高又无法满足特殊环境要求；U型振荡管测量密度一般要求恒温，且长时间测量会使内壁生成污垢导致测量精度下降。

因此本文提出一种差压式检测[5]方式对蓄电池电解液液位和密度进行测量，并对测量时的相关问题进行探讨。

1 压差检测系统设计

1.1 检测原理

流体静力学分析可知，液体的液位高度和密度直接影响其所产生的压强大小，差压检测就是基于此原理来实现的。图1所示为差压测量原理图，两个规格相同的标准传感器[6-8]探头安装在高度差为△h的位置，当放入一定深度的液体中会产生不同的压强。

图1 压差测量原理图

P1=kρgh1

(1)

P2=kρg(h1+△h)

(2)

式中：P1为传感器探头1在距液面高度h1处产生的压强；P2为传感器探头2在距液面高度h2处产生的压强；k为压差系数；g为当地重力加速度；ρ为液体的密度。

由式(1)、式(2)可得出未知溶液的密度和液位。

(3)

(4)

由式(3)、式(4)分析可知，只要能检测出一定高度差处的两点压强，既可实现对液位和密度的同时检测。测量过程中受温度、大气压力、气泡、安装误差、压差测量精度、液体涌动等外界环境因素的影响，会对传感器的精度、线性度和稳定性等静态特性造成严重干扰。因此，必须综合考虑外界环境因素对测量系统的影响。

1.2 检测系统设计

本次实验主要针对电解液的液位和密度进行监测，结合数据采集系统，设计出一套合理的压差检测系统。

测量过程中传感器作为主要元件，必须进行合理的设计以达到实验要求。传感器应变材料[9-10]受到均匀分布且大小恒定的压力作用时，应变材料将发生弯曲变形，通过应变桥将实际应变转换为便于处理的模拟量输出。

由于应变材料易受温度的影响，且受到冲击载荷时容易损坏。为防止被测介质对敏感元件造成损伤，一般采用膜片隔离方式。在隔离膜片和敏感元件间充满液体介质，既保证了压力的传输效果，又能降低压力突变对敏感元件的冲击。硅油的热膨胀系数小，低温环境不易冻结，高温条件不易挥发和气化，且其粘度不随温度变化而变化，同时也能保证压力传递的稳定性，于是成为首选的填充液。根据文献[11]可知硅油的运动粘度η0和温度t之间的关系式为

η0=-2.59×10-7t3+9.75×10-5t2-0.0139t+0.861

(5)

波纹膜片受到外界压力时轴向变形线性度好、灵敏度高、可根据需要调整多种参数等优点，可作为传感器的隔离膜片。波纹膜片的种类很多，根据膜片表面纹理形状可以分为正弦波形、梯形波形和三角波形膜片。由于正弦波膜片是圆角过渡，可避免应力集中且加工相对容易，一般采用正弦波形的波纹膜片，其结构如图2所示。

膜片的结构为正弦曲线形式，正弦曲线的表达式为

(6)

式中：A为幅值；T为周期；φ为初相位。

图2 正弦波纹膜片结构图

膜片应具有优良的回弹特性和耐腐蚀性质，材料的储能越大则传感器的稳定性越佳，储能公式

(7)

式中：σp为材料弹性极限；E为材料弹性模量。

通过对材料特性的比较，最终选用钽合金作为膜片材料，其参数如表1所示。

表1 膜片材料物理参数

1.3 膜片受力模型及有限元分析

膜片尺寸参数较多，对变形的影响复杂，力学方程不能完全适合对膜片的分析。综合膜片的压力特性、工艺条件等因素确定膜片的尺寸参数。

膜片的压力特性方程如式(8)所示。

(8)

式中：P为均布压力；R为膜片工作半径；m为膜片厚度；Kp为弯曲刚度系数；Lp为拉伸刚度系数；Ap为无纲量刚度系数；Bp为无纲量拉伸非线性系数；W0为中心变形量。

由式(8)可知，膜片的变形与膜片厚度、材料的力学特性、膜片半径等多种因素有关。

为达到最佳应变效果，对膜片进行有限元分析，有限元模型为圆形波纹膜片，分析其受到均匀载荷作用时膜片的变形特征。

通过指派材料、3D网格划分、添加约束、施加载荷、求解等一系列过程，可模拟出不同参数的膜片受力变形情况。图3为膜片均匀载荷受力图。图4 为膜片边界约束和施加均匀载荷图。

图3 膜片均匀载荷受力图

图4 膜片边界约束和施加均匀载荷图

有限元分析可知，其他条件一定，随着膜片直径的增加，相同压力作用时中心变形依次增大；相同直径的情况下，膜片厚度越大，膜片的中心变形越小；膜片厚度和膜片直径一定时，波纹高度越大，中心处的最大位移量越小，最大应力也越小。有限元分析和理论设计一致，最终选用如表2所示参数的波纹膜片。

表2 波纹膜片参数 mm

2 实验及结果分析

2.1 实验设备

为提高测量的精度和准确性，本实验用带有光栅尺可进行反馈调节的高精度Z轴来控制液位的高度，液位调节可达到1微米；使用恒温装置控制测量温度，防止环境温度对测量数据产生误差；使用数显仪表进行数字化处理，数显仪表一般能进行量程调节，提高测量精度；用标准密度计进行标定。测试仪器结构组成如图5所示。

2.2 标定和系统测试

由压强公式(1)可知，压力大小与液体液位和密度有一定的比例关系。不同液体在相同的外界环境条件下，由于液体的密度不同，在相同的液位高度时也会产生大小不同的压力。为定量检测液体的液位和密度，需要确定传感器在不同液体中的压差系数k，对传感器进行校准和标定。

图5 测量仪器结构组成图

利用标准的密度计测量出已知溶液的密度ρ，然后将自制的压力传感器放入一定深度的溶液中，此时数字控制面板能够读取所在液位高度，数字采集表头能够读出对应的示数，记录此时的压力大小P1和液位高度h1，然后将传感器移动一定高度，记录此时的压力大小P2和液位高度h2，将数据填写到labview程序前面板的对应位置，通过调整压差系数k使计算出的密度等于ρ，求得传感器在液体中的压差系数k，标定完成。labview程序框图和前面板如图6、图7所示。根据式(1)，密度ρ的单位g/cm3，重力加速度g的单位N/kg，高度h的单位mm，则P的单位为Pa，即数字仪表的单位为Pa。

为测量传感器的非线性误差和灵敏度。在标准密度溶液中，标定好的传感器多次改变液位高度，记录多次液位值和压力值。

图6 labview运算程序框图

图7 labview运算前面板

2.3 测试结果与分析

液位高度和压力关系的实验测试结果如图8所示，液位高度和对应的压力值正相关。

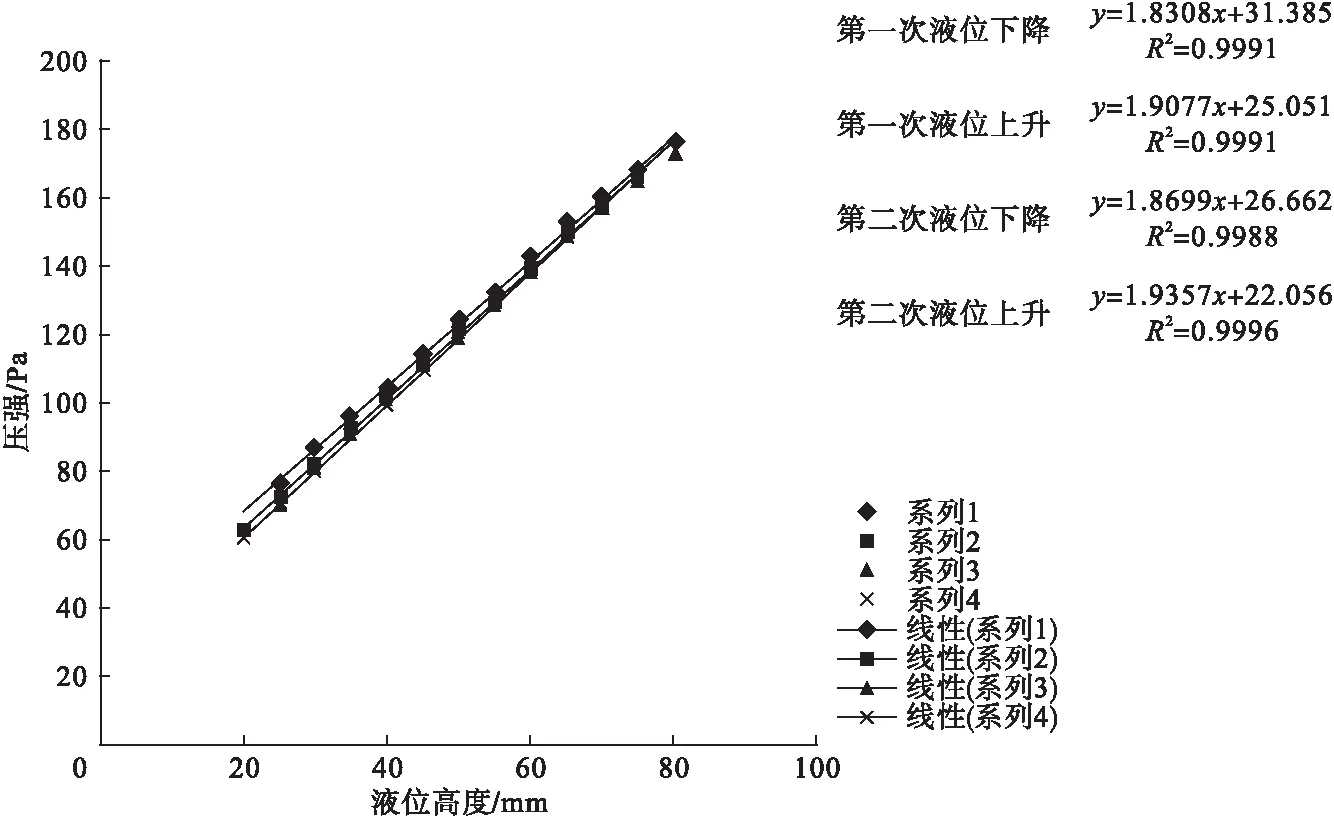
图8 液位高度与压力关系图

对实验结果中的散点图进行拟合，得出数据的拟合直线及相关系数。

假设拟合直线方程为

y=jx+b

(9)

若实际校准测量点个数有n个，则第i个与拟合直线上响应值之间的残差为

Δi=yi-(jxi+b)

(10)

(11)

从而求出j和b的表达式为

(12)

(13)

对图9中数据进行处理，得到拟合线性度系数R2及直线斜率j。R2越接近1，说明传感器的线性相关性越强。残差的最大值即为非线性误差，通常用相对误差γL来表示，即

(14)

式中：ΔLmax为最大非线性误差；yfs为满量程输出。求得灵敏度和非线性误差，如表3所示。

表3 灵敏度和非线性误差

表3结果表明，该测量系统的非线性误差较小，灵敏度高，能够满足对液位和密度的测量。

2.4 测量误差影响因素分析

一般压力传感器受温度变化的影响很大,特别是在低温高压环境下,压力传感器应变材料的电阻率、压阻系数、泊松比及弹性模量等因素都会发生变化,这些变化导致测试结果与实际情况产生差异。环境温度会造成传感器线性度降低、传感器零点漂移等问题；所测液体密度也受温度的影响。所以，测试过程中要进行温度补偿；为防止温度对测量结果造成影响，实验过程中保持恒温测量。

分析检测原理可知，压差传感器的安装高度差和压力差大小将直接影响测量精度。实际测量过程中的压差传感器，由于加工和装配误差，实际和设计的高度差有一定误差，会导致计算结果出现误差。本次实验测试过程中，计算出的高度差是两次液位的差值；实际上，由于传感器的体积使液位上升，致高度差出现误差，影响标定的标定系数。

实验是通过压力差来计算液位密度，为提高测量的精度，必须精准测量一定高度差的两点之间的压力差。根据检测的液位高度和安装高度差，需要选择合适量程的传感器。在满足测量的条件下，量程越小，传感器分辨率越大，测量精度越高。实验采用的数字仪表量程可调，最大限度的降低了测量误差。

此外，液体中的气泡也会对测量数据产生较大影响；不同重力加速度也会对实验结果产生一定影响；为达到最佳测量效果，需将这些误差影响因素消除或减弱到最低水平。

3 结束语

基于差压原理研究液位与压强之间的关系，并对压力传感器进行模型分析。通过理论分析，推导出压强、液位、密度三者之间的比例关系，实现了液位和密度的一体化测量，能够节省检测空间，提高测量效率。对压力传感器和膜片进行分析设计，运用标准传感器进行标定，标定后对传感器的静态特性进行测量，非线性度误差较小，回归分析拟合线性度系数R2接近于1，线性较好。实验过程中减小干扰因素对测量结果的影响，提高了测量精度，满足对液位和密度的高精度测量。