青龙桥锚拉板结构优化设计

魏庆庆， 张树清

(安徽省交通规划设计研究总院股份有限公司; 公路交通节能环保技术交通运输行业研发中心，安徽 合肥 230088)

0 引 言

目前大跨径斜拉桥或是独塔混合梁斜拉桥，为了减轻自重，主梁通常采用钢箱梁构造型式。此类桥梁的斜拉索与钢箱梁之间的连接是否安全可靠一直是设计重点关注的问题之一。索梁连接结构要将斜拉索传递来的巨大索力传递到主梁，是一个局部应力大、传力复杂的区域。

斜拉索与钢主梁的锚固主要有以下几种形式：① 锚箱式；② 散索鞍加锚固梁；③ 锚管式连接；④ 支架或牛腿；⑤ 耳板式(销铰式)连接；⑥ 锚拉板。其中，锚拉板式索梁锚固结构因其受力明确、施工简单、便于加工、易于维护的结构特点使之得到了广泛的应用[1]。

锚拉板式索梁锚固结构是将锚拉板与主梁顶板直接焊接，分上、中、下三个部分，由承压板、锚拉筒、锚拉板、加劲板及加强板等组成，如图1所示。 锚拉筒与锚拉板通过焊缝连接， 锚拉板接焊在主梁梁顶板加强板上，正下方是腹板，锚拉板上还焊有加劲板。 斜拉索穿过锚拉筒，锚固在锚拉筒的承压板上[2]。

图1 常规锚拉板构造示意图

锚拉板的设计是否合理，直接关系到全桥的结构安全。本文依托引江济淮工程青龙桥，参考国内外设计案例，根据空间有限元计算结果，对锚拉板构造的设计进行了些许探索。

1 工程概况

引江济淮工程青龙桥位于安徽省合肥市肥西县上派镇，是青龙潭路横跨派河桥梁，状桥梁不满足引江济淮工程Ⅱ级航道净空要求，需拆除重建，如图2所示。

图2 青龙桥老桥(左侧)、改建新桥(右侧)

青龙桥主桥为独塔钢-混凝土混合梁斜拉桥，跨径组合为(140+80) m，桥宽42 m。主梁采用混合梁，主跨为钢箱梁，边跨采用混凝土梁。拉索锚固于外腹板钢箱梁顶板，采用锚拉板构造，拉索横向中心间距为27.5 m，梁上索距12.0 m。

2 锚拉板构结构受力分析

根据国内外已建成钢箱梁斜拉桥的锚拉板构造，青龙桥锚拉板初步按照如图3所示构造进行设计。

图3 青龙桥原设计锚拉板构造

青龙桥钢箱梁侧斜拉索共10对，修正后斜拉索倾角范围在22.5～60.7°，索力成桥索力值3 050～5 182 kN。选取索力最大的M10锚拉板建立有限元模型进行研究。M10锚拉板各项参数见表1。

表1 M10锚拉板参数

2.1 有限元模型建立

斜拉索索力的施加：根据圣维南原理，分布于弹性体上一小块面积(或体积)内的荷载所引起的物体中的应力，在离荷载作用区稍远的地方，基本上只同荷载的合力和合力矩有关；荷载的具体分布只影响荷载作用区附近的应力分布。计算模型中将索力值等效为锚垫板上的均布压力荷载，可按下式计算：

P=F/A

式中：F为拉索索力，A为锚板受力面积[3]。

青龙路桥斜拉索为平面索，钢横梁对锚拉板的计算影响比较小，且本文主要对锚拉板锚固点附近的构造优化，因此可忽略主梁的影响，在与主梁连接的部位采用固结约束[4]。采用软件MIDAS FEA进行局部分析，锚拉板各部分采用板单元模拟，锚拉板有限元模型如图4所示。

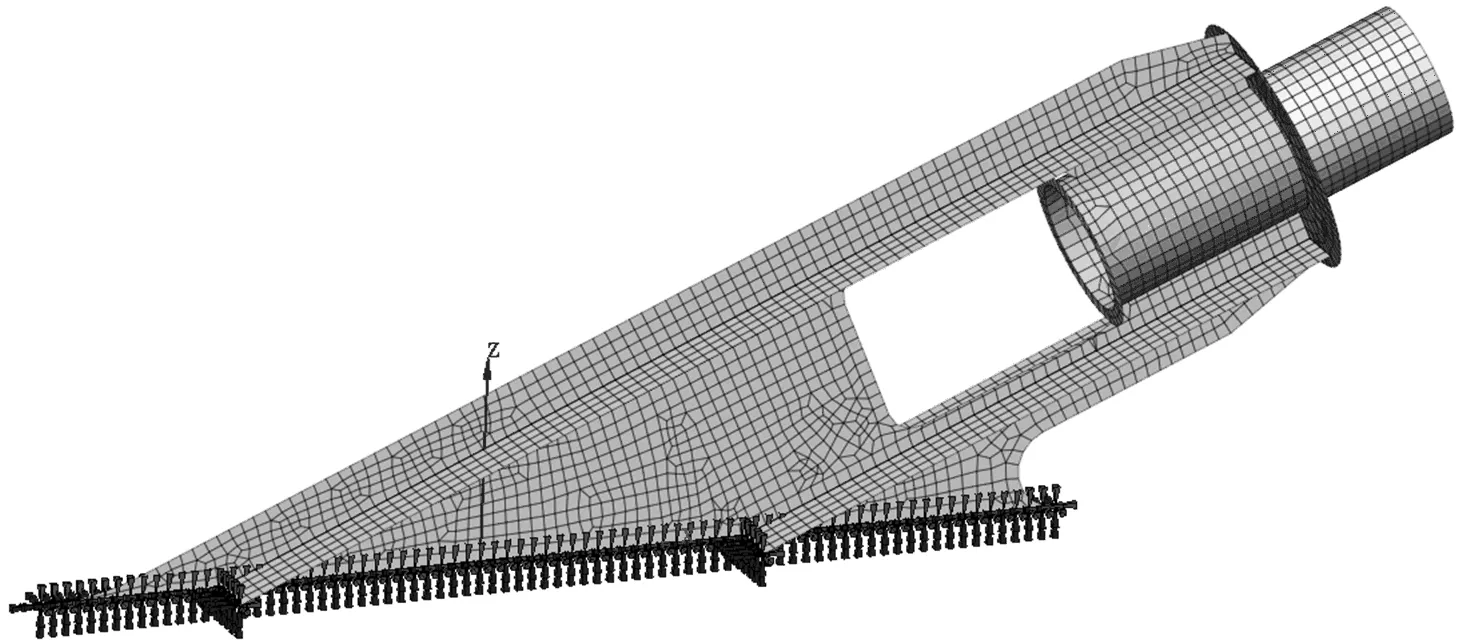
图4 锚拉板有限元模型

2.2 结果分析

锚拉板各组成部分一般在双向或三向复杂应力状态下工作，判断各构件应力是否超限不能通过单一方向应力决定，需要能够反映各方面应力影响的“屈服条件”来确定。理论上，对于有明显屈服强度的材料，试验证明应用材料力学的第四强度理论能较好地反映钢材的弹塑性工作状况。在FEA中对于各项同性的材料主要采用Von Mises 屈服准则下的应力作为等效应力[5]。

(1)锚拉板：计算结果表明，锚拉板最大等效应力为467.6 MPa，出现在上部开口倒角的位置，如图5所示的A位置。锚拉板绝大部分区域应力较低，97.2%的部位处于204.9 MPa以内。

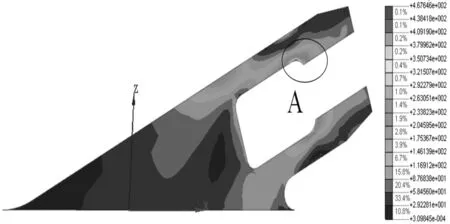
图5 锚拉板等效应力云图(单位：MPa)

(2)钢锚管：钢锚管最大等效应力为452.3 MPa，在锚垫板附近，如图6所示的B位置。远离斜拉索张拉位置，应力迅速衰减，约96%的区域处于293.4 MPa以下。

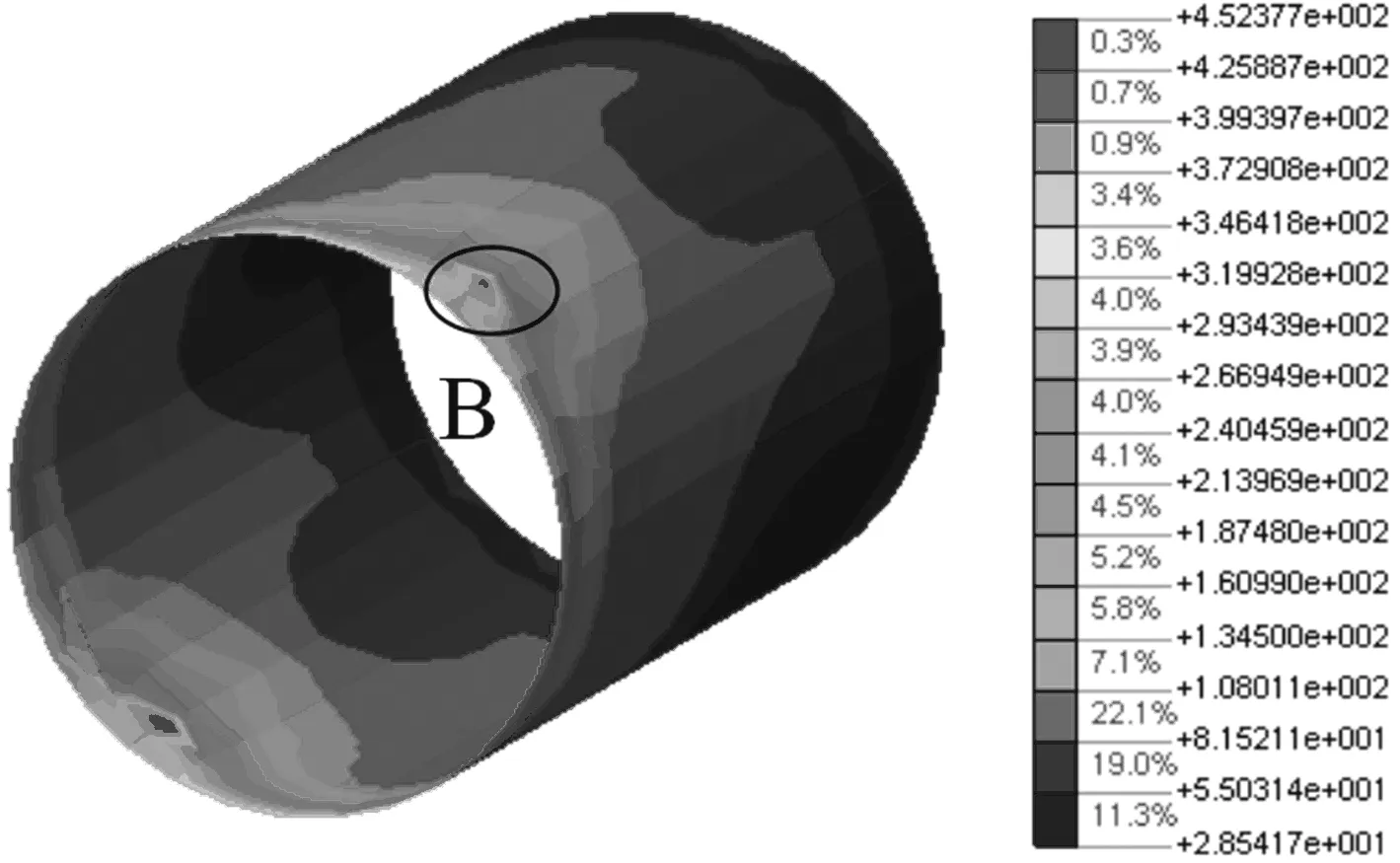
图6 钢锚管等效应力云图(单位：MPa)

(3)加劲板：加劲板最大等效应力为195.1 MPa，出现在锚拉板上部开口倒角位置，如图7所示，96.2%的区域均处于112.8 MPa以下。

图7 加劲板等效应力云图(单位：MPa)

(4)锚垫板：锚垫板最大等效应力为314.5 MPa，如图8所示，位于锚垫板的最上部位。

图8 锚垫板等效应力云图(单位：MPa)

由计算结果可知，锚拉板绝大部分区域应力较低，但是局部应力较大，峰值应力突出。参考国内外相关桥梁资料，在设计中一般通过加大板厚、材料规格或者其他构造措施来降低局部应力。然而，为了降低大约2%板件范围的应力，对整个板件的尺寸进行加大，事实上是不够合理也不经济的。

2.3 锚拉板优化设计

通过有限元计算结果可知，锚拉板应力较大的部位主要集中在锚垫板之后很小的范围。因此，结构优化的方向应是通过设置一些构造来分散锚拉板、锚管承担的力，快速地将斜拉索传递来的巨大索力传递出去。

通过望东长江大桥、寿春西路桥等工程项目的探索，发现通过增加锚拉板、锚管加劲的方式，如图9所示，能够十分有效地降低应力峰值。

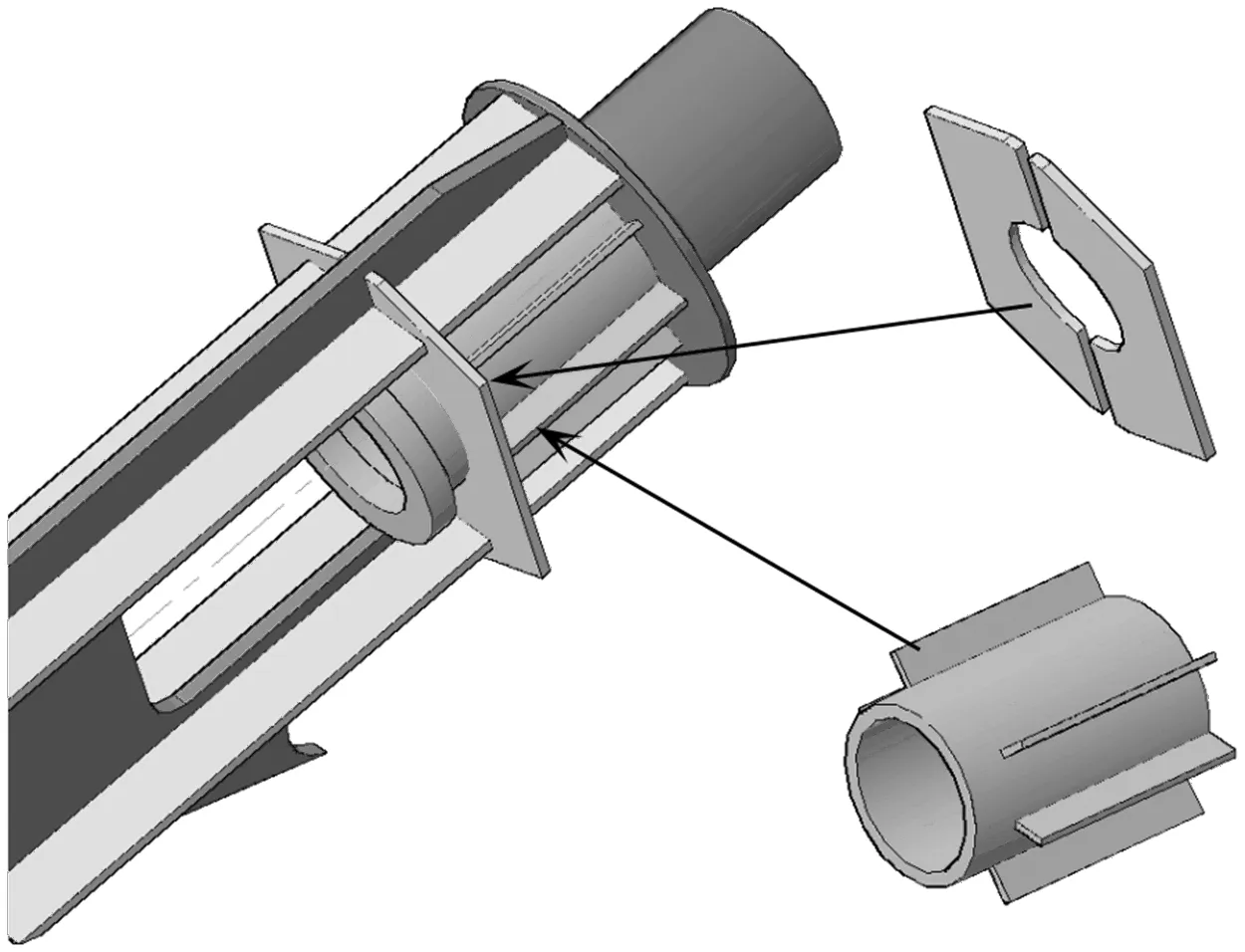
图9 锚拉板增加加劲板示意

按图9构造示意增加锚拉板加劲板，加劲板的板厚均为20 mm，初步测算钢材仅增加约50 kg。利用FEA建立有限元模型，得到前述各板件在加劲后的应力结果。限于篇幅，此处仅介绍锚拉板及锚拉筒的应力结果，如图10、图11所示。

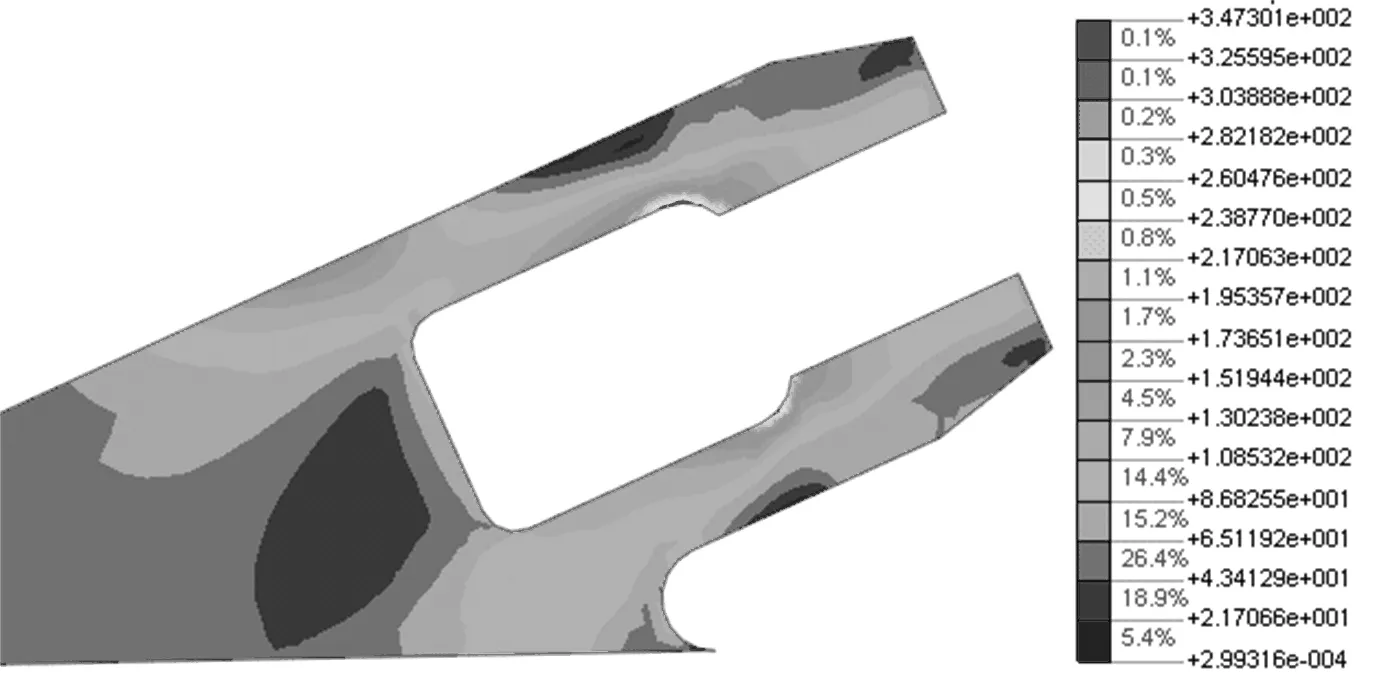
图10 锚拉板最大等效应力(347.3MPa)

图11 钢锚管最大等效应力(406.4MPa)

对上述两种构造形式下的峰值应力进行整理，对加劲效果进行评估，对比结果见表2。

表2 锚拉板优化前后最大等效应力对比

通过计算结果可知，仅通过增加少量加劲肋，锚拉板各部位峰值应力下降了至少10%。对于需要采用高强钢材的锚拉板及锚拉筒，峰值应力的降低，意味着能够采用尺寸更小、强度要求较低的构件，从而能够大大节省材料，获得比较理想的经济性。

3 结束语

锚拉板这种结构形式在钢箱梁斜拉桥的索梁锚固中应用得越来越普遍，国内外已经有许多成熟的经验。本文通过分析对比青龙桥锚拉板两种不同的构造型式下应力变化情况，得出如下结论：锚拉板可以在增加较少量的加劲板的情况下，来达到降低关键部位峰值应力，从而达到较好的经济性。本桥在既有锚拉板经验的基础上做了些许尝试，希望对今后类似桥梁的设计能够起到借鉴与参考的作用。