基于改进PSO优化RBF神经网络线损计算与分析

何立强，赵 允，于景亮

(国网丹东供电公司，辽宁 丹东 118000)

随着经济的不断发展，电能消耗逐渐增多，然而在这快速增长能源消费的背后，是低效率的能源利用方式和由于管理水平、技术水平带来的高线损。线损是考核电力企业运行经济性和技术管理水平的重要指标，但目前配电网线损计算及判断窃电位置还存在不足。若能够充分利用有限的测量值，分析线损值和窃电位置之间的关系，就能够更好辅助配电运检人员直观判断是否有窃电行为的发生。

传统线损指标管理以人工统计为主，受统计周期影响，线损率波动严重，“大月大”、“小月小”的问题无法解决，业务数据集成度不高，跨专业业务流程和工作界面不清晰，线损异常处理周期长，业务数据的准确性、真实性、集成度不高，缺乏过程精益管控，掩盖了线损管理中存在的问题，降低了其在电网企业管理中应发挥的监控、指导作用。同时线损管理中的“跑冒滴漏”尤其是窃电等不法行为一直是“老大难”问题，更是呈现出高科技化、隐蔽化、大额化特征，严重损害了电力公司的经济利益。现场人工查找效率低、精度差，用电信息采集系统采集了海量数据，但不能智能分析研判。

传统的计算方式已经不能满足当前大数据、多计算、难统计的要求，应用先进的机器学习可以有效解决上述问题，大量的数据可以使学习模型更为精准和使用。同时，智能算法通过数据驱动的形式，大大简化了电网的复杂程度，使得其计算难度大幅度下降。文献[1]提出了一种使用 Levenberg-Marquardt(LM)算法优化的 BP 神经网络的重要参数，利用上述模型拟合样本线损率和电气特征参数之间的关系，从而得到线损变化规律。文献[2]提出了一种灰色关联分析和改进神经网络的 10 kV 配电网线损预测方法，更加高效的对线损值进行了预测。文献[3]提出了一种基于随机森林算法的台区合理线损率计算方法，由于该方法输入中加入了多源数据，相比传统方法具有更快的计算效率。文献[4]利用神经网络构建理论线损计算模型和窃电位置分析模型，通过理论线损和统计线损的比较得到窃电位置。文献[5]建立遗传算法优化神经网络模型，该方法减少了线损的计算误差和计算时间，提高了稳定性。

本文首先改进PSO( Particle Swarm Optimization)算法中权值的变化规律，其次利用改进PSO算法优化RBF神经网络 ( Radial Basis Function)，分别从理论线损计算和管理线损两个方向出发，基于某地区的负荷母线分布和潮流分布建立配电网络模型，进行线损计算，同时依靠线损值建立窃电位置模型，对该地区是否发生线损及发生位置进行准确判定，并通过Matlab/Simulink仿真验证了该模型的准确性。

1 改进PSO优化RBF神经网络模型的建立

1.1 RBF神经网络结构

RBF神经网络具有3层结构，分别为输入层、输出层和隐含层[6]，其网络结构如图1所示。

RBF神经网络的特点是输入层至隐含层为非线性变化，而隐含层值输出层为线性变化。非线性变化时的映射函数φ为

φ(||x-ui||)

(1)

式中:x时输入;ui是第i个隐含层节点。

同时由于映射函数是高斯函数，也可以表示为

(2)

继而可以得到RBF神经网络为

(3)

式中:yi为第j个输出节点;ωij为第i个隐含层到第j个输出层的连接权值。

RBF神经网络的关键是确定激活函数的宽度φ、隐含层的接地节点ui和权重值ω。本文使用改进PSO算法对权重值进行优化。

1.2 改进PSO算法

PSO算法是一种随机搜索算法，相对于其他算法具有参数少、迭代速度快、不易陷入局部最优值，具有较好的全局收敛能力[7-8]。

在一个种群数量为N的群体中，每个粒子的搜索范围是M，M大小取决于问题本身。每个粒子的搜索方向和速度分别为

Xi=(xi1,xi2,…，xiM),i=1,2,…，N

Vi=(ui1,ui2,…，uiM),i=1,2,…，N

(4)

第i个粒子的位置记为该粒子当前最优值

Pbest=(pi1,pi2,…,piM),i=1,2,…,N

(5)

整个种群最优位置为

gbest=(pg1,pg2,…,pgM),g∈{1,2,…,N}

(6)

粒子速度和位置更新公式为

(7)

式中:c1、c2为学习因子；r1、r2为随机数；ω为惯性权重。

惯性权重值的变化影响了收敛速度，常规的优化惯性权重的方法为随机权重法、线性减小权重法等，本文对惯性权重的变化规律给予改进增强了算法的搜索能力。惯性权重变化规律表达式为

(8)

式中：w0为初始权重值；wmax为最大迭代次数时的权重值；tmax为最大迭代次数；tcur为当前迭代次数。

2 理论计算与窃电分析模型的建立

2.1 理论线损计算模型

理论线损时指电力传输过程中线路损耗的电能，传统线损计算经常利用潮流计算，同时使用功率平均法、均方根电流法和损耗因素法计算理论线损值。传统计算方法计算工作量大，不适用于低压配电网络。因此，本文采用改进PSO优化RBF神经网络对理论线损值进行求解。具体实现如下。

a.输入和输出量

已有的潮流数据作为输入量，理论线损值作为输出量，可得：

(9)

式中：Ss和St分别为统计线损和理论线损；f为线损计算函数；Pi、Qi分别为第i个负载的有功和无功功率；Pgi为发电机的发电功率。

b.数据获取

随着配电网络的不断发展，已能够较为完整的获得各台区的网络结构参数，因此可以通过前推回代潮流算法得到各个节点的负荷参数。

c.训练样本的选择

本文中采用K-S法从潮流分布的各个节点参数中选取训练样本，保证样本的空间遍历性，可以有效提高网络模型的精确度和训练速度。

采用IPSO-RBF神经网络通过已有的潮流数据作为输入，理论线损值作为输出，作为训练样本训练得到模型。此时，理论线损值和统计线损值大小相同。

2.2 窃电后理论线损计算模型

将窃电发生后的表计数据再次进行潮流计算，使用IPSO-RBF神经网络计算模型得到窃电后的理论线损值:

(10)

(11)

式中:ki为母线i上的窃电率。

由于模型输入的功率等潮流数据未发生变化，因此窃电后的统计线损值不变。由此得到了窃电发生时的理论线损值和统计线损值，将两者的差值作为判断窃电发生的依据。

2.3 计算与分析模型的建立

本文的最终目的是通过改进PSO优化神经网络的模型建立配电网络多潮流场景的线损计算模型，同时基于线损数据建立该台区窃电位置判断模型。改进PSO优化神经网络的主要思路是：首先将采集的线损数据归一化处理，其次对RBF神经网络参数极性初始化，使用改进PSO算法对神经网络权重值进行优化，最后使用优化后的RBF神经网络中进行理论线损值的计算和窃电位置分析。具体步骤如下:

a.对配电网潮流分布数据统一归一化处理，使用改进聚类法确定神经网络中隐含层数量，运行参数；

b.改进粒子群算法参数初始化，计算当前迭代次数下的适应度值，利用改进权重值的变化规律对权值更新；

c.计算当前粒子运动速度和位置，并更新粒子的适应度值、Pbest和gbest；

d.判断迭代次数是否达到最大，如果没有则继续进行步骤2，如果达到则停止输出；

e.将得到的gbest作为解码成为神经网络中的权重值，计算激活函数宽度；

f.对测试样本进行测试得到最优网络参数计算测试样本值；

g.分析得到理论线损值；

h.将窃电后的表计数据再次重复步骤a-g，得到统计线损值；

i.将统计线损值、理论线损值和接入负荷作为输入，判断窃电位置。

3 仿真分析

为了验证本文方法的有效性，对某地区低压配电网络进行仿真试验，搭建标准IEEE13节点配电网络，该网络标准容量为100 MVA，基础电压为23 kV，配电网结构如图2所示。

3.1 算法参数设置

对输入数据归一化处理，将数据归一至[-1,1]区间内，归一化函数为

(12)

式中:ymax、ymin分别为1和-1;xmax、xmin分别为数据中最大值和最小值;y为归一化后的值，x为原始值。

神经网络隐含层数量为11个，训练函数采用梯度下降法，神经网络迭代次数设置为8000次，学习步长为0.1，精度设置为0.01%，激活函数为

(13)

式中:n为前一个神经元传递输入值，其值域为(-1，1)。

使用改进PSO对神经网络的权值进行优化。设定种群规模为30，惯性系数初始值ω0=0.8，c1=2，c2=2，r1=0.5，r2=0.6，最大迭代次数为40采用新的权重值变化规律对权重值进行更新，其适应度值变化曲线如图3所示。

由图3可以看出，改进权值变化规律后PSO算法收敛速度更加迅速，经过3次迭代就可以收敛，有效提高了模型的计算效率。

3.2 理论线损计算模型仿真

考虑现实情况下出现切除、投入负荷和负荷波动的情况进行如下的数据采集：

a.负荷大范围波动(±45%)400组；

b.负荷小范围波动(±15%)400组；

c.切除部分负荷，每次切除一个负荷点，共计520组。

最后，得到数据总和为1320组，其中随机选取高负荷波动20组，低负荷波动20组，符合切除情况数据24组，共计64组数据作为测试样本，其余数据作为训练样本进行训练。神经网络的有效输入量为24组数据，为配电网中24个PQ节点对应的有功和无功值，输出为理论线损值。收敛结果如图4所示，其与实际值相比误差如图5所示。

从图4和图5可知，低负荷组、高负荷组及切除负荷组，除一组误差超过4%以外，误差值基本保持在3%之内，可以看出模型是精准和有效的。

3.3 窃电位置分析模型仿真

将理论线损值分别带入经过改进PSO优化后的神经网络和标准神经网络的窃电位置分析模型中，其结果分别如表1、表2所示相比标准RBF神经网络分析模型，改进PSO优化神经网络分析模型在整体窃电判断上具有更高的准确性，改进模型的泛化识别效果明显高于前者。但是该模型在低窃电分析和三窃电分析仍旧识别率较低。为了提高模型的准确度，本文通过增加训练数据的数量提高模型的泛化能力，增加三窃电发生数据300组，增加4%窃电情况数据300组，再次进行相同方式训练，其训练结果如表3所示。

表1 标准RBF神经网络分析结果

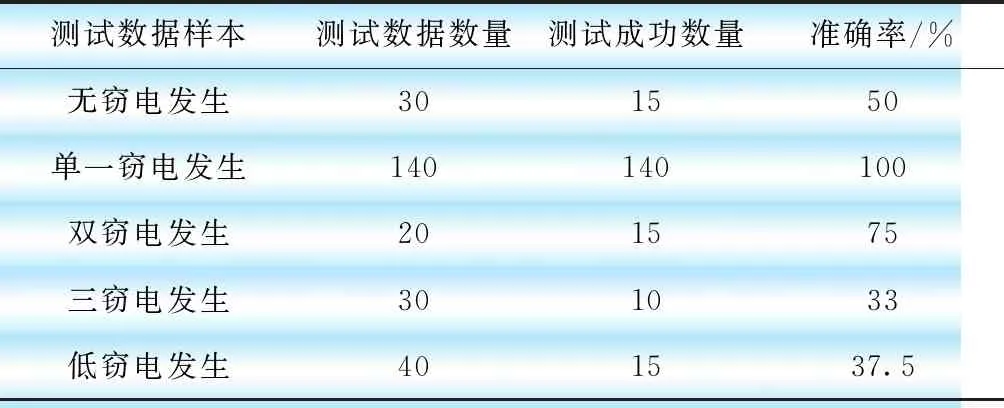
表2 改进PSO优化RBF神经网络分析结果

表3 增加训练样本后的训练结果

由表3可见，通过增加训练样本数据，提高了模型的泛化能力，其中三窃电发生和低窃电发生判断准确率有了明显提高，模型整体判断准确率较高。

4 结束语

本文以传统理论线损计算模型为基础，使用智能算法对理论线损值进行了求解，同时使用新的权重值变换规则对粒子群算法进行改进，使用改进后的粒子群算法对神经网络的权重值进行优化，有效地提高了计算速度和计算精度。最后，在典型线路范围内验证了模型的可行性。

在仿真分析中，理论线损计算的准确性能够保持较高的水平，同时依靠改进PSO优化RBF算法在窃电位置分析中取得了较好的效果，在多种窃电位置分析判断中具有较高的精度。