基于主要状态识别的涡轴发动机载荷谱研究

滕怀亮，李本威，韦 祥，张 赟，王永华

(海军航空大学 航空基础学院，山东 烟台 264001)

载荷谱是航空发动机整机及零部件的应力分析、寿命监控、结构设计以及可靠性分析的基础条件。美军的B-1轰炸机、F-16战斗机等发动机均出现了耐久性问题，其原因主要是与原设计任务谱相比，发动机的实际使用载荷谱条件更为严苛，循环情况更复杂[1-3]。进行发动机零部件试验时，根据已有的飞行数据编制载荷谱是需要首先解决的具有挑战性的工作[4]。国内宋迎东[5-6]，赵福星[7]等对发动机载荷谱的相关工作进行了深入研究，但涡轴发动机的载荷使用特点与涡喷、涡扇发动机相比有较大不同[8]，在编制载荷谱时应予以特别关注。

编制涡轴发动机载荷谱的一个主要问题在于确定其主要工作状态及持续时间。顾永根[9]，杨兴宇[10]等在划分发动机状态时采取确定某参数保持平稳的时间段，并将其作为一个状态的方法。宋迎东等[11]采用平滑处理和多参数同时稳定的方式识别发动机载荷状态。上述文献中确定不同发动机不同参数稳定状态范围的上下限主要依赖经验，或直接采用设计状态，而涡轴发动机的实际载荷与设计状态相比有很大差异。本文依据雨流计数低幅值转速循环的分布规律，利用聚类的方法确定了发动机实际使用过程中的主要工作状态。

编制载荷谱的另一个主要问题是处理众多的发动机载荷循环类型，一般采用压缩等效的方法，将众多的循环类型归类为几个典型的循环类型[10,12]。压缩等效时需要依据根据疲劳、蠕变和热冲击损伤一致的原则[8]，保证载荷谱和实际飞行任务谱的一致性。史海秋等[13]研究了某型发动机承力机匣疲劳载荷谱的编制方法，但只分析了与转速成线性关系的应力循环的等寿命线形式，没有给出通用的等寿命带划分方法。本研究推导了等寿命线的转速循环峰谷值表达形式，给出了基于等寿命线和发动机实际主要工作状态的距离判别方法，将发动机的众多循环状态归类为11种主要循环。

1 涡轴发动机主要工作状态

该型直升机飞行过程中多数不会用到发动机的设计转速状态ng,d，因此多数飞行剖面的主循环峰值转速nmp小于设计转速，且发动机实际使用的主要工作状态普遍小于设计状态，需要获取发动机实际使用过程中的主要载荷状态及循环情况。根据疲劳理论，包含相同的循环数的两个载荷谱对零部件造成的疲劳损伤基本相同，所以要提取实际飞行任务数据的载荷循环。小幅值循环反映了转速在某一状态附近的小幅波动[14-15]，其密集分布的区域实际上反映出发动机转速主要工作在以该类循环的均值为代表的工作状态，因而可以利用小幅值循环的分布规律确定发动机的主要工作状态。

1.1 雨流计数

循环计数的方法主要分为单参数计数法和双参数计数法，双参数计数法中的雨流计数因其与应力变化过程一致而在工程中得到了广泛应用[14]。如图1所示，引用文献[14]中的例子对雨流计数法进行检验和说明，其中1、3、5、7、9为谷值点，2、4、6、8为峰值点，雨流计数规则可以总结为雨流的起点和终点两个部分：

1) 起点：雨流从各峰谷值1-9点内侧开始向下流；

2) 终点：从峰值开始的雨流到峰值更大的点对应的时间即停止；从谷值开始的雨流到谷值更小的点对应的时间即停止；遇到上面落下的雨流即停止。

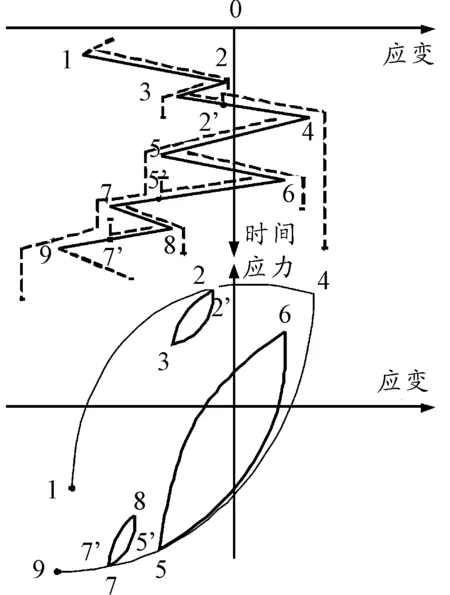
图1 雨流计数示意图

保留起点时间作为循环开始时间，终点时间与起点时间之差作为循环持续时间。相邻两个雨流若峰谷值相同则构成一个全循环，如2-3-2’，若不相同，则自成一个半循环，如1-2-4。经验证，程序统计结果与手工统计结果一致，得到全循环：2-3-2’，5-6-5’，7-8-7’和半循环：1-2-4，4-7-9。选取某次飞行的转速-时间剖面，对其进行雨流计数后，共得到1861个循环，并获得了每个循环的幅值、均值、循环开始时间和循环持续时间、循环类型(半循环：用0.5表示或全循环：用1表示)，部分循环信息如表1所示。

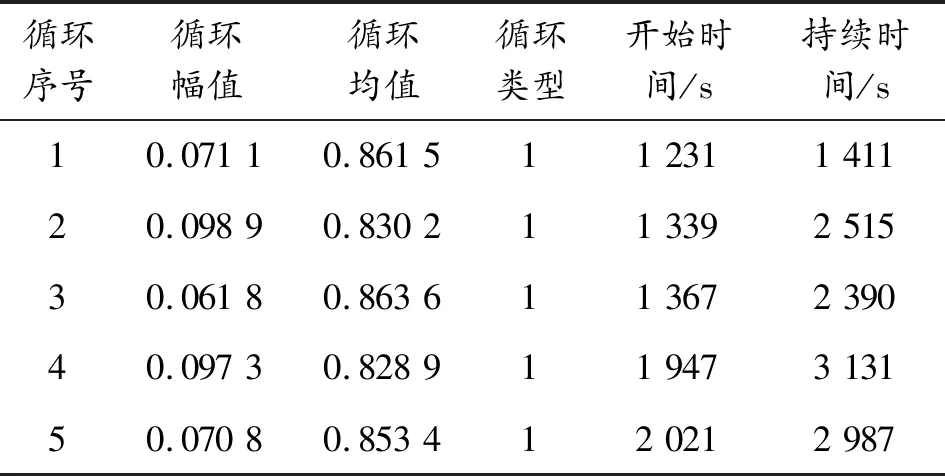
表1 雨流计数结果

统计所有循环均值、幅值的不同区间的循环数，如图2所示，高均值、低幅值的循环数最多，即主要工作转速区间的小幅值循环较多；高幅值循环数较少，即对零部件造成疲劳损伤较大的循环较少。将各个循环以“谷峰值对”的形式作为横纵坐标在图中表示出来，如图3所示。从图3可以发现，实际载荷循环包含大量接近零幅值的小幅值循环，且分布呈现围绕几个主要工作状态聚集的簇状分布。

图2 雨流矩阵示意图

图3 转速循环在峰谷值等寿命线中的分布图

1.2 主要工作状态识别

对于转动件，影响蠕变的主要参数为转速。转速保持相对稳定的阶段即为发动机的稳定状态，使用频次大的转速状态则为发动机的主要工作状态。

如图4所示，黑色表示载荷变化过程，彩色表示雨流计数的循环情况，该过程中有一个大幅值循环，其余均为围绕某一均值的小幅值循环。小幅值转速循环实际为转速较为稳定状态下的循环，所以可以通过对小幅值循环进行聚类进而确定发动机的主要工作状态。k-means聚类算法具有速度快和可扩展性良好等特点，在数据处理等领域得到了广泛的应用[16]。进行聚类要选定分类数据集的属性，根据小幅值循环的峰谷值分布情况，采用峰谷值对作为分类属性，但k均值聚类算法的劣势在于需要预先确定分类数目，在不知道最佳分类数的情况下，可以采用肘部法确定最佳分类数[17]，首先定义一个数据对象和其所在的聚类域的目标函数，然后通过不同分类数目对应的目标函数值的大小评价聚类效果。常用的目标函数是中心误差平方和J。

其中：xi为第j类数据中的第i个数据向量；μj表示第j类数据的中心向量；向量xi的维数为数据的属性值个数，在本例中即为峰值和谷值两个；Nj为第j类数据中的数据个数；k表示数据分类的数目。

计算不同分类数的目标函数值即平均畸变程度J值，其变化规律如图5所示。选取肘部位置的分类数5作为最佳分类数，得到目标数据的分类情况及各类别中心如图6所示。

图4 稳定状态示意图

图5 不同聚类数的平均畸变程度曲线

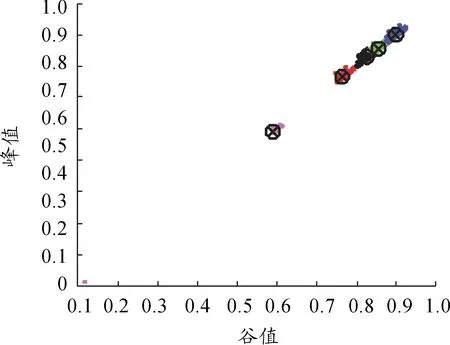
图6 数据分类情况及聚类中心图

根据聚类中心峰谷值可以得到峰谷值均值对应的主要状态，如表2所示，其中实际使用主要状态1(0.591 4)和状态2(0.759 0)与发动机设计地慢(0.598 8)和设计空慢(0.748 5)状态非常接近。但使用时间最长的巡航状态(0.827 3、0.852 1)和最大状态(0.901 9)均远小于发动机的设计状态(即起飞状态)(1.000 0)。

表2 主要状态的时间分配情况

这是因为该型直升机发动机三发总功率比直升机所需功率大很多，所以执行训练任务时，发动机的实际使用状态要小于设计使用状态，单纯使用巡航、最大连续、起飞等设计状态进行分析会与实际使用载荷状态有较大出入。依据主要载荷状态，可以将发动机主要循环类型分为表3所示的11类。

表3 主要循环类型

2 循环类型压缩

编制发动机载荷谱的另一个主要问题是处理类型众多的循环。单次飞行的转速数据，忽略雨流计数的小幅值循环后，仍然有几十个循环类型，在工程应用中对所有载荷剖面进行零部件和寿命分析是非常困难的，所以需要进行循环类型压缩。压缩时需要遵循疲劳、蠕变及热冲击损伤等效的原则，蠕变和热冲击损伤等效时需要保证载荷状态及循环类型较为接近。疲劳损伤的等效需要依据等寿命线，将非脉动循环转化为脉动循环。为在归类转速循环时将与转速幅值有关的疲劳损伤和与发动机状态有关的热冲击损伤和蠕变损伤统一起来，需要推导等寿命线的转速表达形式。

2.1 等寿命线相关参数标准化

为在统一标准下进行比较，需将燃气涡轮转速ng换算至标准大气条件下的换算转速ng,c，并利用该型涡轴发动机燃气涡轮最大转速将其化为标准化转速n，n∈[0,1]。

如图7所示，某转速循环的最小值(即谷值)为nmin，最大值(即峰值)为nmax。应力幅σa，平均应力σm如式(1)、式(2)所示

(1)

(2)

图7 正弦转速循环与应力循环曲线

根据发动机旋转件的局部应力-应变特点，离心应力与转速的平方成线性关系：

σ=σmv+a·n2

(3)

式中：σmv为0转速时的残余应力；a为转速和应力之间的比例系数；n为转速。

若该型发动机最大转速ng,d对应的应力为σmp时，则标准化后的应力循环对应的均值σm、幅值σa及强度极限σb分别为

式中，σb为材料的强度极限，根据需要分析的旋转件材料进行选取。

如图8所示，等寿命线的表达式变为式(4)

(4)

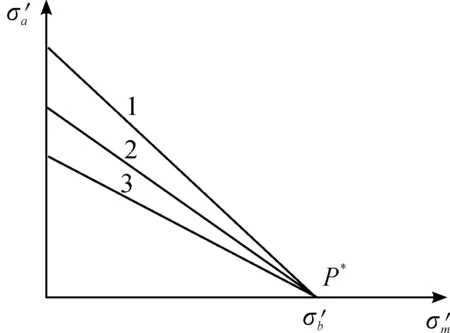
图8 等寿命线

2.2 等寿命线转换

定义转速的幅值函数Na和均值函数Nm如式(5)、式(6)所示：

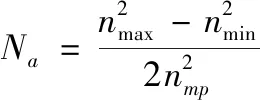
(5)

(6)

则由式(1)—式(3)可得

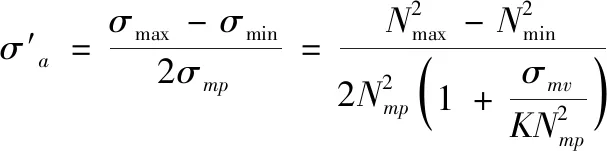
代入式(4)，可得

(7)

令

式(7)变为式(8)

Na=k(Nm-b)

(8)

一般取b=1.2，即等寿命线辐射点为P(1.2,0)，由式(8)可知图8中的等寿命曲线123就转化为图9中PB、PC、PD。

图9 转速循环等寿命线

其中，OA线表示谷值为0的脉动循环，AF线表示峰值为最大转速nmp的循环，所以OAF三角形内侧表示旋转机械工作区域。ABCD分别对应峰值转速为nmp、0.9nmp、0.8nmp、0.7nmp，谷值为0的脉动循环。ABCD对应的转速幅值函数Na的值可以由式(7)计算得到，进而求得不同寿命的等寿命线所对应的斜率kPA,kPB,kPC,kPD。

由Na=k(Nm-b)可以得到峰谷值之间的函数关系式

(9)

其中ki为不同等寿命线的斜率，i=1,2,…,10时分别对应转速谷值为0、转速峰值为0.1nmp、0.2nmp、…、0.9nmp的脉动循环所在等寿命线，如k9=kPB,k10=kPA。可以得到以峰谷值表示的等寿命线如图10所示，3条红色边界线nmax=1，nmin=0和nmax=nmin分别表示峰值转速为最大转速的循环、谷值转速为最小转速的循环和循环幅值为0的转速循环。可以看出，推导出的等寿命循环的峰谷值关系满足公式(9)，该公式的优势在于在考虑疲劳损伤的同时，没有忽略高均值低幅值循环造成的与状态变化相关的热冲击及蠕变等损伤，可以在同一标准下根据主要循环状态将造成热冲击损伤较大、疲劳损伤较小的高均值低幅值循环考虑进来，使得载荷谱更接近实际载荷状态。

2.3 判别归类

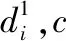
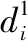
图10 峰谷值表示的等寿命曲线

3 编制模拟任务试车谱

根据飞行数据编制模拟任务试车谱的流程如图11所示。雨流计数得到载荷循环信息，对小幅值循环进行k-means聚类，确定主要状态和主要循环类型，依据等寿命线和主要循环类型，通过距离判别压缩大幅值循环类型，得到模拟任务载荷谱。

3.1 数据预处理

飞参数据中存在很多等值点，将转速大小相同的相邻各点合并为1个点，该转速点对应的时间为各相邻等转速点的时间均值。同时，需要将超出转速范围及传感器误采集等原因造成的不符合实际情况的数据剔除，或对其进行平滑处理。雨流计数前需要先提取峰谷值，判断第i个转速点ng(i)是否为峰谷值，即判断相邻两点与该点的差值ng(i)-ng(i-1)和ng(i)-ng(i+1)是否同号[18]：若两转速差异号，则ng(i)非峰谷值；若两转速差均为正，则ng(i)为峰值，若均为负，则ng(i)为谷值。

图11 编制载荷谱流程框图

3.2 生成载荷谱

根据疲劳理论，小于疲劳极限的载荷循环造成的损伤可以忽略，所以只需保留造成疲劳损伤较大的大幅值循环。疲劳极限可以作为舍弃小幅值循环，保留大幅值循环的临界点。在具体分析时应根据分析对象的不同，利用零部件材料S-N曲线确定应力疲劳极限，计算其对应的转速。本文取疲劳极限对应转速为0.2npm，经雨流计数后舍弃小幅值循环，得到大幅值速循环和主要循环状态在等寿命线中的分布情况如图12所示。

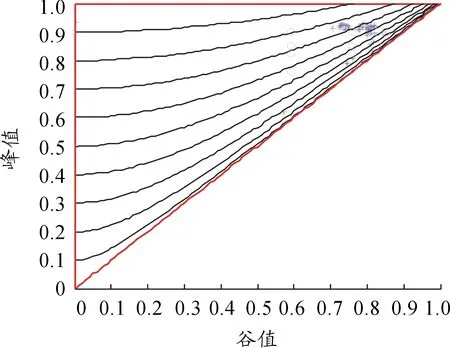
图12 大幅值循环和主要循环类型在等寿命图中的分布

根据2.3节的距离判别公式，将造成疲劳损伤较大的51个转速循环归类为表4所示的11类循环。由表4所列的判别归类结果可以看出，该型涡轴发动机主要循环类型为空慢-最大-空慢和巡航-最大-巡航。

3.3 载荷谱生成及方法验证

将判别归类后的转速按循环开始时间进行排序并连接。根据蠕变理论，各级载荷大小和保持时间相同的两个载荷谱对零部件造成的蠕变损伤相同。主要状态的保持时间可以由属于该类别的低幅值循环的循环时间确定，统计该次飞行中5种类别的低幅值循环的持续时间[19]，得到5种主要状态的持续时间比例，如表2所示。根据总飞行时间生成平均分配各状态的持续时间，保证每个状态的总持续时间与实测载荷谱相同，生成如图13所示载荷谱。

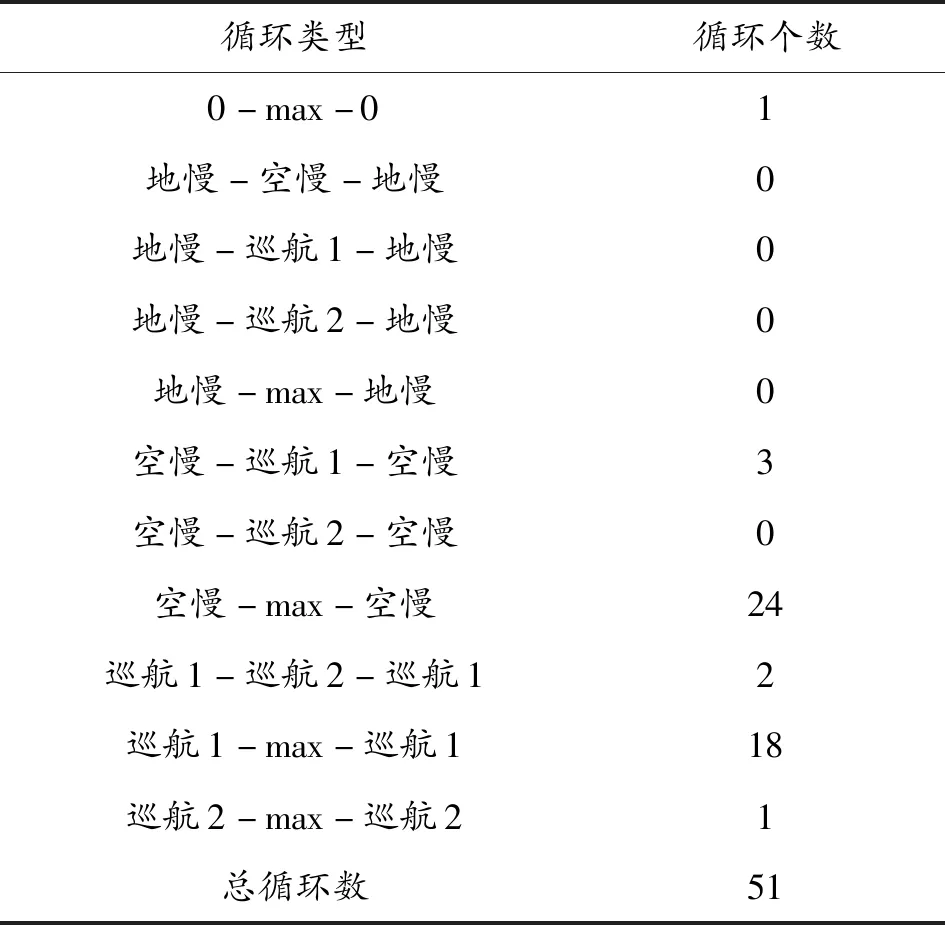
表4 主要循环类型的计数结果

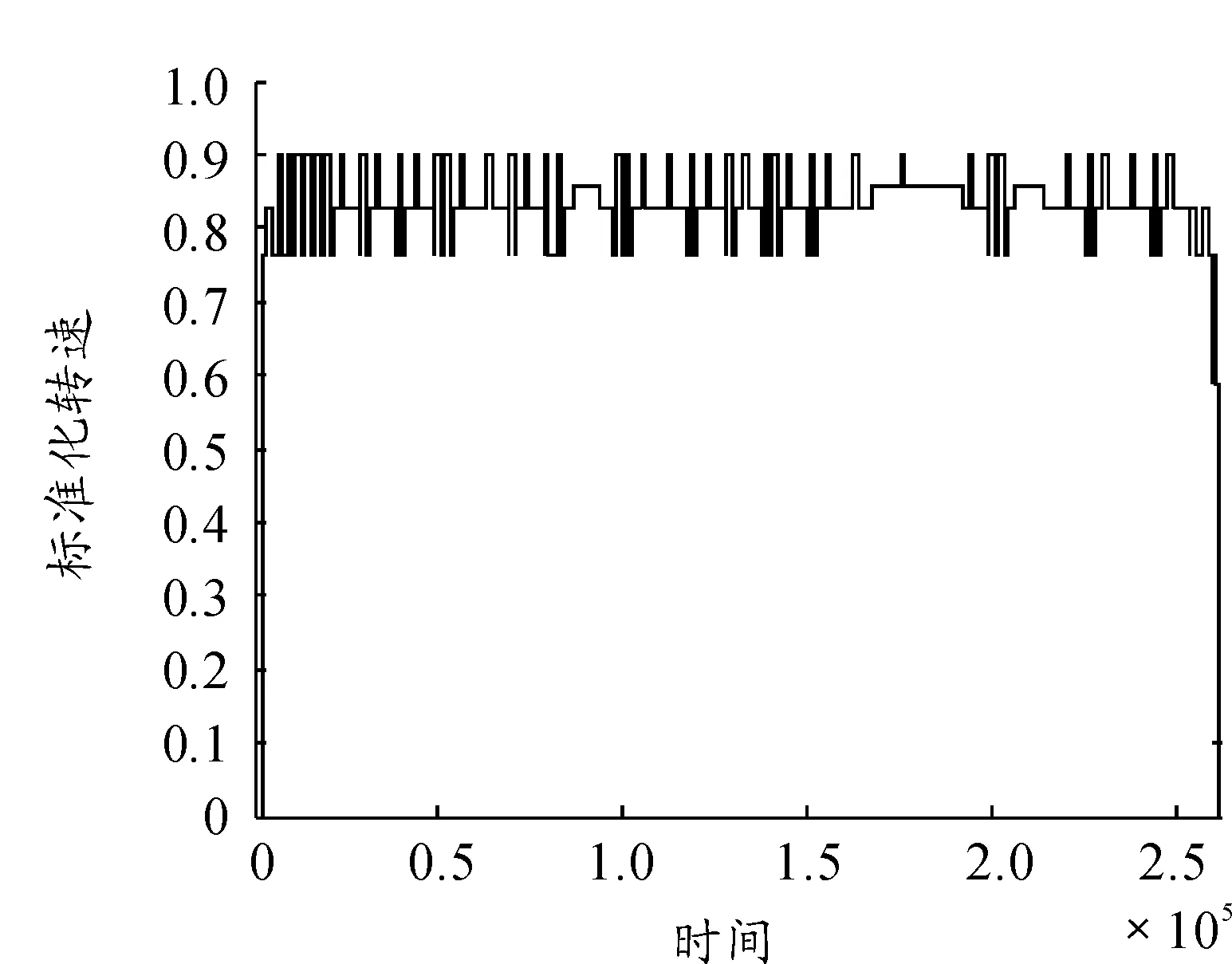
图13 模拟任务载荷谱

涡轴发动机的使用可分为训练飞行、任务飞行和地面维护开车三部分，训练飞行是使用的主要部分。选取训练飞行某一科目3个架次的3台发动机共9组飞行数据进行对比分析，比较同一发动机不同飞行架次，以及同一飞行架次三台不同涡轴发动机的主要状态误差情况、循环类别分散度情况，对比情况见表5及表6所示，序号1-1表示直升机第1飞行架次的1号发动机。由于同一飞行架次的三台发动机使用载荷状态较为接近，从表5可以看出，该方法识别的主要状态误差较小，保持在5%以内。

表5 主要状态误差对比

表6 主要状态误差对比

从表6可以看出，同一飞行架次的各循环类型数量较为接近，第2和3飞行架次的2发循环数与1发循环数和3发发循环数有部分区别，主要由于2发进气环境不同导致发动机循环状态与1发循环数和3发发循环数不完全匹配。

4 结论

1) 实际载荷历程通过雨流计数后得到大量接近零幅值的小幅值循环，且其峰谷值呈现围绕几个核心状态的簇状分布，通过对其峰谷值的聚类确定发动机的实际主要工作状态，同一飞行架次的三台发动机主要工作状态的识别误差在5%以内；

2) 实际使用转速载荷循环以高均值小幅值循环为主，造成疲劳损伤较大的大幅值循环较少，但高均值低幅值循环造成热冲击及蠕变损伤不可忽略。推导出以转速循环的峰谷值表示的等寿命线，利用该曲线进行循环类型压缩时可同时考虑疲劳、热冲击和蠕变损伤；

3) 该型涡轴发动机实际使用的地慢与空慢状态与设计转速较为接近，实际使用的巡航及最大载荷状态远小于设计状态；实际使用过程中的主要循环类型为空慢-最大-空慢和巡航-最大-巡航。