基于共因失效贝叶斯网络的鱼雷现场使用可靠性评估

王新鹏，张静远，王 鹏，徐振烊

(海军工程大学兵器工程学院，武汉 430033)

现代鱼雷是复杂的水下精确制导武器，组成鱼雷的部件种类繁多，包含电子、机械、机电、橡胶等[1]。鱼雷从出厂到寿命终结分贮存、装载和实航3种典型的状态，在服役过程中，鱼雷会经历多次的贮存、装载和实航过程[2]。对于部件而言，不同的状态条件下环境不同，部件承受的应力不同，造成部件的故障规律不同，且部件之前经历的状态也会对其可靠性变化规律产生影响。目前在对鱼雷或部件进行可靠性分析时，单纯考虑鱼雷在某种状态下的可靠性规律，没有结合鱼雷现场使用实际[3-4]。例现场使用条件下，鱼雷贮存一段时间后经技术准备检查完好后，转入装载后的可靠性与单纯在转载状态的可靠性相比，虽均是从1开始变化，但变化规律发生变化。因此，有必要研究实际现场使用条件下鱼雷系统可靠性。

本研究按照由部件到系统的思路，在已知部件单一状态故障规律的基础上，研究现场使用条件下部件的可靠性变化规律。在此基础上，建立基于传统贝叶斯网络和考虑共因失效的贝叶斯网络的鱼雷系统可靠性评估模型，分别利用两种分析方法对系统故障概率、部件重要度和后验概率，并进行对比分析。该方法为分析鱼雷系统现场使用的可靠性变化规律和确定系统的薄弱环节提供指导。

1 经历多个状态的部件可靠性分析

1.1 条件可靠度

条件可靠度的定义：当故障时间为T的一个产品单元在t=0时开始工作，一直正常工作到时间t，那么该产品单元再正常工作x时间的可靠度为[5]

R(x|t)=Pr(T>x+t|T>t)=

(1)

对于鱼雷装备而言，设某类型部件在贮存状态的可靠性变化规律为R1(t)，在装载状态的可靠性变化规律为R2(t)，在实航状态的可靠性变化规律为R3(t)。

根据条件可靠度的定义，假定贮存时间t1后，经技术准备检查完好，鱼雷转入装载状态，则该部件在装载状态的可靠性变化规律变为

(2)

其中，R2(t20)=R1(t1)。

假定贮存t1时间后，经技术准备转入装载状态，装载t2时间后，经检查鱼雷功能正常，转入实航发射状态，其在实航状态下的可靠性变化规律变为

(3)

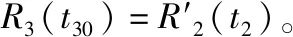
以此类推，可以计算任意时刻在任意状态的部件的可靠性变化规律。

特别地，当部件可靠性变化规律为指数分布时，设在贮存状态下满足R1(t)=e-λ1t，在装载状态下满足R2(t)=e-λ2t，在实航状态下满足R3(t)=e-λ3t。贮存时间t1后经技术准备转入装载，则在装载状态下的可靠性变化规律为

(4)

贮存时间t1后，经技术准备后装载时间t2，功能正常，转入实航状态，其在实航状态下的可靠性变化规律变为

(5)

由此可见，可靠性变化规律服从指数分布的部件在某种状态下的可靠性变化规律没有发生变化，与之前的经历无关。

1.2 参数估计

对于故障分布函数F(t)为威布尔分布和对数正态分布的部件，需根据式(1)进行计算，然后利用最小二乘法对其分布进行参数估计。

1) 威布尔分布的参数估计

威布尔分布的分布函数为

F(t)=1-e-tm/t0,m>0,t0>0,t≥0

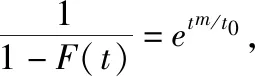
(6)

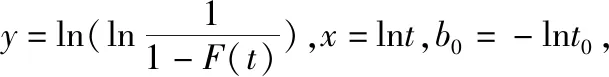
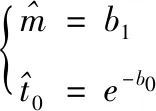
(7)

2) 对数正态分布的参数估计

对数正态分布的分布函数可写为

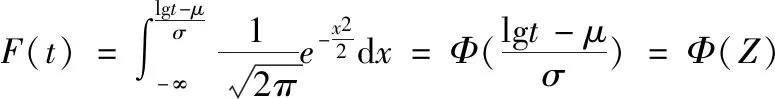
式中：Φ(Z)指标准正态分布的分布函数，有

(8)

令x=lgt，则x=σZ+μ等同于y=b0+b1x。因此，对于Z和x的一组数据，同样可以用最小二乘法计算回归系数b0,b1和相关系数r，并得到对数正态分布参数的估计为

(9)

求得经历多个状态后的部件故障分布函数后，利用考虑共因失效的贝叶斯网络模型对鱼雷系统的可靠性进行分析。

2 考虑共因失效的贝叶斯网络模型

共因失效(Common Cause Failure，CCF)是一种源于某种共因的多重故障，这种故障普遍存在于工程系统中，增大了系统各故障模式的联合故障概率，降低了冗余系统可用度，若忽略系统部件之间的相关性，假设部件故障相互独立的条件下对系统进行可靠性评估容易造成一定的误差[6-7]。目前用于处理共因失效的模型主要有α因子模型、β因子模型、MGL模型等[8-10]。

贝叶斯网络是一个有向无环图(directed acyclic graph,DAG),它由代表变量的节点及连接这些节点的有向边构成[11-13]。贝叶斯网络不但可以实现正向推理,由先验概率推导出后验概率,即由原因导出结果,还可利用公式由后验概率推导出先验概率,即由结果导出原因。

1) 传统的贝叶斯网络模型

设系统由部件X1,X2,…,Xn组成，建立传统的贝叶斯网络模型如图1所示。

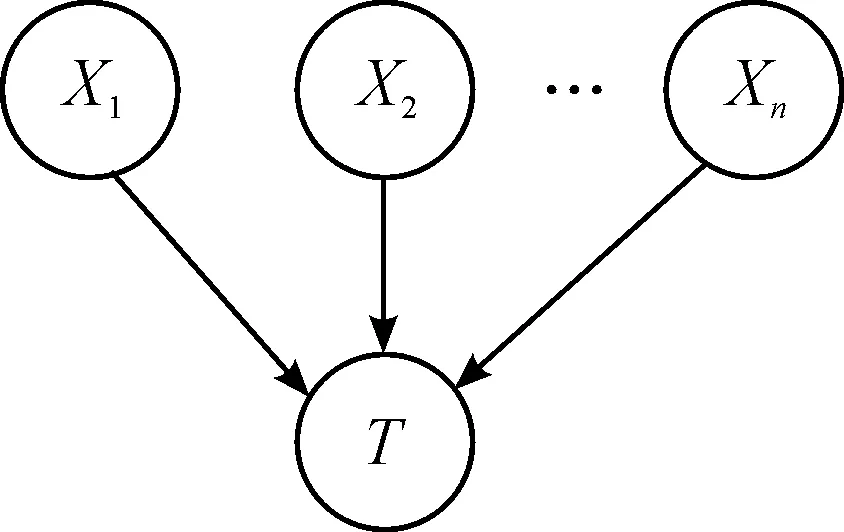
图1 传统贝叶斯网络模型示意图

计算不考虑共因失效情况下系统的故障概率为

(10)

计算系统故障条件下，各部件故障的后验概率为

(11)

利用贝叶斯网络计算各部件的重要度为

概率重要度：

(12)

结构重要度：

(13)

关键重要度：

(14)

2) 考虑共因失效的贝叶斯网络模型

建立考虑共因失效的贝叶斯网络模型的关键时将系统中的共因失效部件的故障率分为独立故障率和相关故障率每个部件串联了一个共因失效部件，此共因失效部件的故障率为两个独立部件的共因失效概率。如图2所示，设系统由部件X1,X2,…,Xn组成，共因失效部件为M，每个独立故障部件和共因失效部件的子节点为M1,M2,…,Mn。

考虑共因失效的贝叶斯网络的系统故障概率计算公式为

(15)

考虑共因失效的部件后验概率及部件的重要度计算，可先求得系统的故障概率，再代入相关公式进行计算。

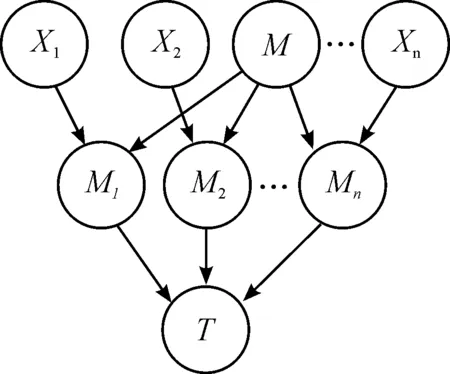
图2 考虑共因失效的贝叶斯网络模型示意图

目前处理共因失效的模型较多，采用β因子模型只需确定一个参数，且不存在数据丢失的问题，故本文采用β因子模型对共因失效事件进行定量分析。假设某部件的总故障率Qt可以分解成独立概率QI和相关概率Qc，通过引入参数β表示相关故障率与组件总故障率的比值：

Qt=QI+Qc

(16)

(17)

对以往共因失效数据的分析研究，得出β因子的一般取值范围为0～0.25(0表示不发生共因失效)，硬件β的因子取值一般为0.01～0.1。在相关部件对外部条件相对敏感的情况下，β的因子取值一般相对较大。此外，为了简化计算分析，当考虑共因失效对系统的影响时，认为共因失效对系统影响是决定性的，即当部件受到共因失效的影响时，部件完全故障。

3 实例分析

假定某鱼雷系统有2个分系统组成，每个分系统由2个关键部件组成，各部件在贮存和装载状态下的故障分布函数和参数，如表1所示。

3.1 经历贮存状态后的部件的装载可靠性分析

该型鱼雷出厂后，在仓库经历1年的贮存后，经技术准备的环节，检查完好，转入装载状态，研究各个部件在装载状态的可靠性的变化曲线。

利用1.1节和1.2节相关内容进行计算和参数估计，得到经历贮存后，在装载条件下部件故障分布函数参数如表2所示。

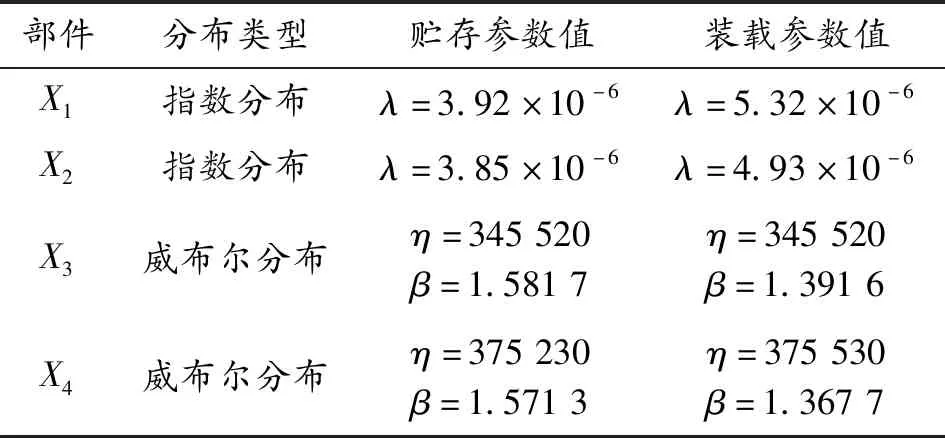
表1 贮存和装载状态下关键部件的故障分布函数和参数

表2 经历贮存状态后部件在装载状态的故障分布

部件X1和X2因故障分布为指数分布，装载状态下可靠度函数不变，部件X3和X4的可靠度变化曲线分别如图3和图4所示。

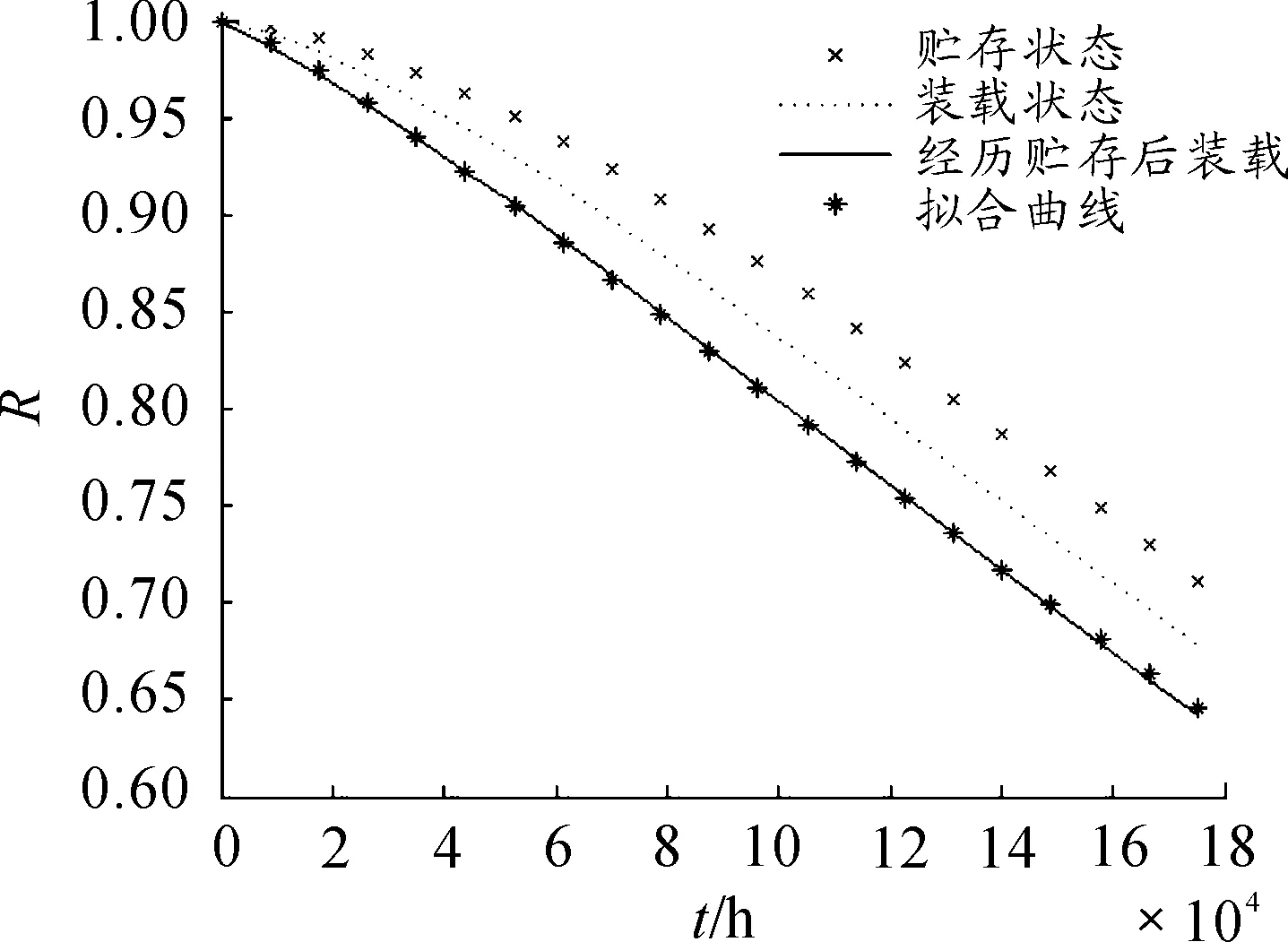
图3 部件X3可靠度变化曲线

图4 部件X4可靠度变化曲线

从其中可以看出，部件X3和X4经历贮存状态，经技术准备转入装载后，装载可靠度较单纯在装载状态的可靠度有所下降。

3.2 考虑共因失效的鱼雷系统可靠性分析

在装载状态下，鱼雷系统中任一部件故障，则认为鱼雷系统出现故障。因此，任一分系统下的两个部件逻辑关系为或门，分系统之间逻辑关系为或门。部件之间是否存在共因失效可以根据故障数据等方法进行分析，假定部件X1和部件X2存在共因失效，建立传统贝叶斯网络模型和考虑共因失效的鱼雷系统贝叶斯网络模型，如图5和图6所示。

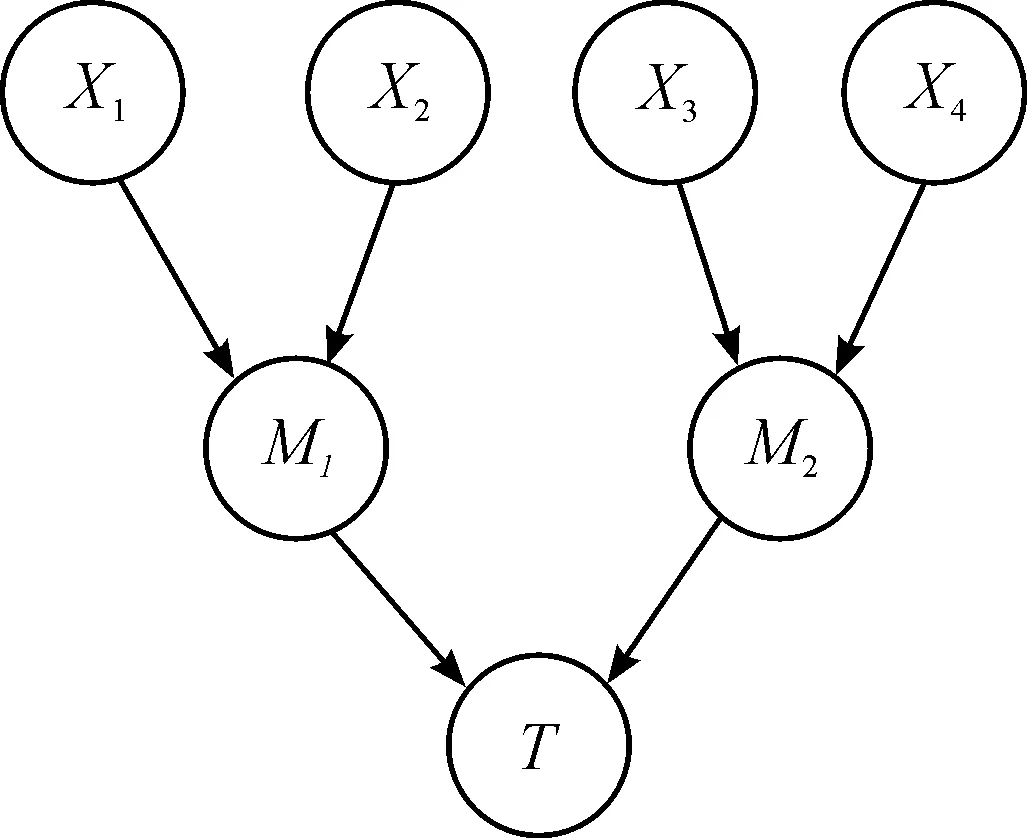
图5 传统的贝叶斯网络模型示意图

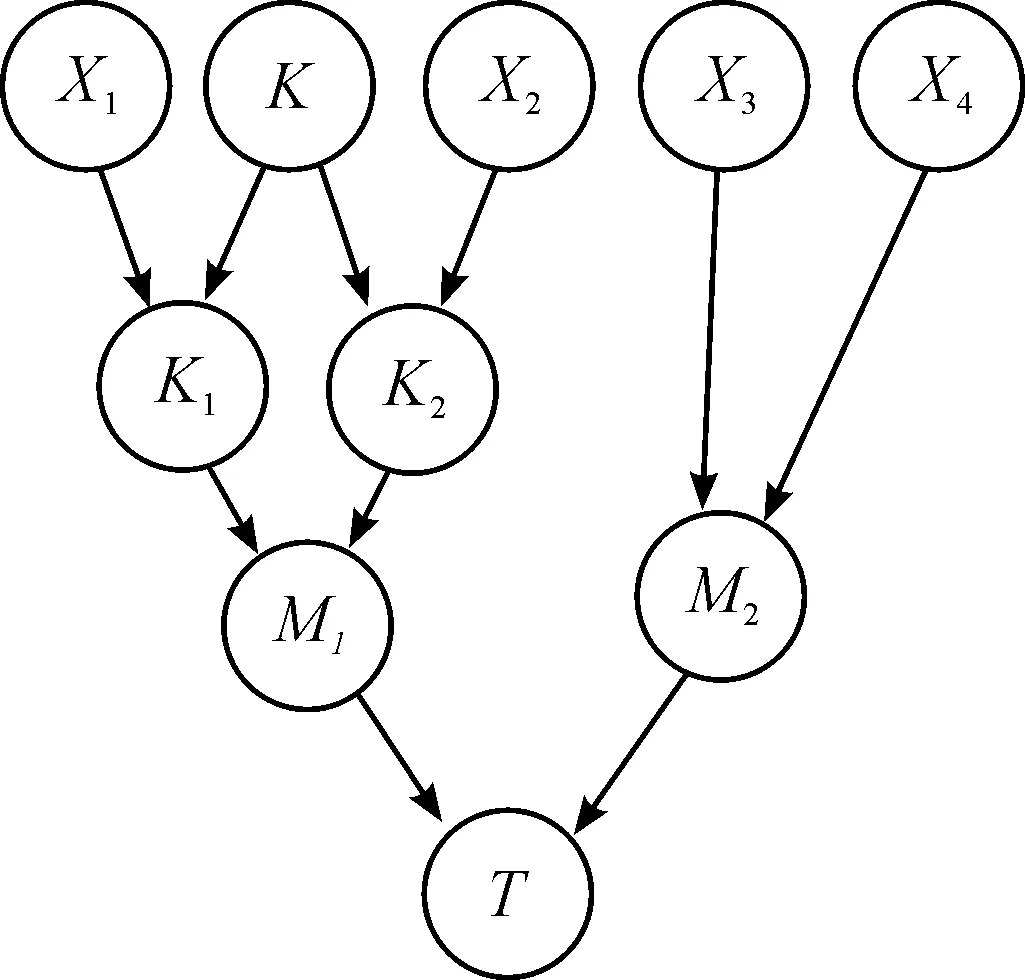
图6 考虑共因失效的系统贝叶斯网络模型示意图

部件X1和X2的故障分布均为指数分布，故障率分别为λ1=5.32×10-6/h和λ2=4.93×10-6/h。采用整合部分法(unified partial method,UPM)对β因子的值进行估计，取部件X1和X2的共因失效因子为0.1。根据β因子模型，部件的独立故障率λ和共因失效率λm的关系为

β=λm/λ

(18)

根据式(18)可以计算出部件X1和X2的共因失效率分别为λ1m=0.532×10-6/h和λ2m= 0.493×10-6/h。因此，部件X1和X2的共因失效率为λm=0.493×10-6/h。

利用传统的贝叶斯网络和考虑共因失效的贝叶斯网络分析方法对鱼雷系统装载1年时的可靠性进行分析。

1) 系统故障概率

传统贝叶斯网络分析方法和考虑共因失效的贝叶斯网络分析方法计算鱼雷系统的故障概率如表3所示。

表3 鱼雷系统故障概率

从表3中数据可以看出，在考虑共因失效的情况下，系统的故障概率高于传统的不考虑共因失效情况下的故障概率。这是因为在考虑共因失效的情况下，共因失效因子会对系统产生影响，因此，考虑共因失效情况下，系统的故障概率计算结果更加精确，更加符合实际。

2) 部件的重要度计算

利用传统贝叶斯网络分析方法和考虑共因失效的贝叶斯网络分析方法对鱼雷系统的部件的概率重要度和关键重要度进行计算，如表4和表5所示。

表4 部件的概率重要度

表5 部件的关键重要度

由于装载状态下，任意部件故障都会导致鱼雷系统故障，所以4个部件的结构重要度是相同的，本节没有进行特别计算。从其中可以看出，传统的贝叶斯网络分析方法计算的概率重要度和关键重要度要比考虑共因失效情况下的贝叶斯网络分析方法计算的结果要大。部件的故障概率越大，计算得到该部件的概率重要度和关键重要度也越大。

3) 部件故障的后验概率

利用贝叶斯网络的反向推理，计算鱼雷系统故障的条件下，各部件故障的后验概率，结果如表6所示。

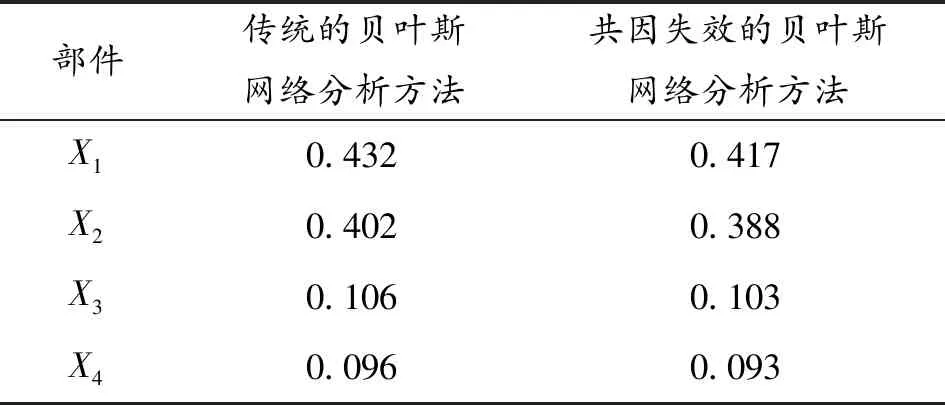
表6 部件故障的后验概率

从表6中可以看出，假定系统故障的条件下传统贝叶斯网络分析方法计算的部件故障后验概率值要大于共因失效的贝叶斯网络分析方法计算的结果。

综上，比较传统贝叶斯网络分析方法和共因失效的贝叶斯网络分析方法的计算结果，可以看出：

1) 考虑共因失效的贝叶斯网络分析方法的鱼雷系统的故障概率升高了，部件的概率重要度、关键重要度和后验概率降低了；

2) 部件X4的先验概率、概率重要度、关键重要度及假设系统故障条件下的后验概率相对来说都是最大的，因此可以判断部件X4是控制系统相对的薄弱环节。

3) 不考虑系统存在共因失效的影响时，会对系统故障概率的计算结果造成误差，共因失效的贝叶斯网络分析方法更符合实际情况，具有更高的计算精度。

图7表示装载1年时，鱼雷系统故障概率随β因子值的变化而发生变化的情况。从中可以看出，随着β因子值的增加，鱼雷系统的故障概率呈线性增加。因此可以通过改善共因失效因子β的值来降低系统故障概率。

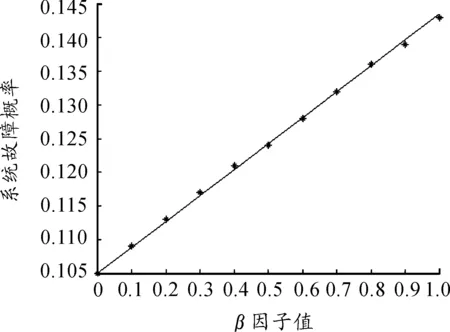
图7 β因子值与系统故障概率的关系曲线

4 结论

利用考虑共因失效的贝叶斯网络分析方法可为鱼雷系统可靠性设计、状态维修和故障诊断提供依据，对求解可靠度等指标、发现潜在隐患和薄弱环节，保证系统的运行安全可靠、避免重大事故发生都具有重要的现实意义。