一个力学问题的巧妙处理及外延类比

邬晨海

(上海市曹杨第二中学，上海 200062)

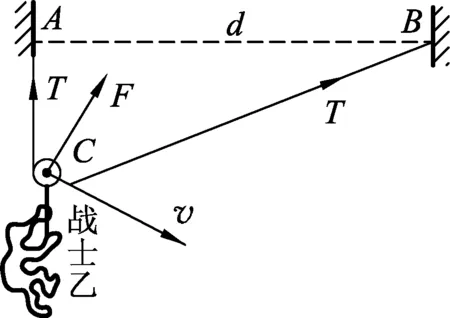
图1

将长为2d的不可伸长的轻绳两端固定在相距d的A、B两个等高点,绳上挂一个理想小滑轮P,战士们相互配合,沿着绳子滑到对面,如图1所示,此时战士甲拉住滑轮,让质量为m的战士乙吊在滑轮上,脚离地,处于静止状态,此时AC竖直,然后战士甲从静止释放,不计绳与滑轮的、滑轮轴心的摩擦以及战士与空气的阻力,不计绳与滑轮的质量,求:战士乙滑动过程中的最大速度．

战士甲从静止释放后,战士乙在重力和绳子拉力的共同作用下向右滑动.由于动点C到两个悬点A、B(定点)的距离之和为常数L,L为绳子的总长度,维持不变,故乙的运动轨迹为椭圆．战士乙在向右滑动的过程中机械能是否守恒呢?

做功的过程就是能量转移、转化的过程.甲物体对乙物体做功的物理意义是甲把能量传递给乙 的过程:人爬楼梯,楼梯没有对人做功,因为楼梯没有对人提供能量的本领;同理,一根孤立的绳子不可能对其他物体做功,因为它不可能对其他物体提供能量.上述情景中的绳子不可能对人做功,因为它不可能对战士乙提供能量,因此战士乙的机械能守恒．

平时所看到的绳子做对物体做功,我们可能看到的只是绳子的一部分,绳子的末端有人或者机械(未画出)通过绳子对物体做功,人或者机械才是能量的来源,在这类过程中绳子只是传递能量而不输出能量．

绳子没有对战士乙做功,绳子对滑轮及人的作用力F和战士乙的速度v方向垂直,F位于绳子AC与BC的角平分线上,速度v的方向沿椭圆的切线,F的指向是动点C到定点A、B的连线的角平分线．

上述力学情景让人联想到椭球面反射镜具有这样的特点: 任意一个焦点发出或通过该焦点的光,经椭球面反射镜后都汇聚到另一个焦点．图2中入射光线AC对应图1中的TAC,反射光CB对应于图1中的TCB;入、反射光线分居在法线两侧,与法线的夹角相等;滑轮两侧绳子拉力大小相等,它们分居在合力F的两侧,与合力F的夹角相等．

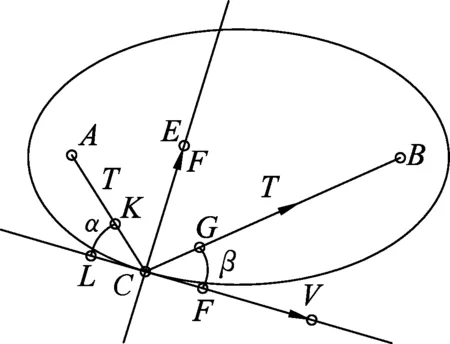
图2

这一光学特征在生活中有很多的应用,医学上的体外碎石技术就是其中的一例(图3)．医学上用来对付肾结石,让肾结石位于椭圆的一个焦点位置,在另一个焦点位置处释放高能冲击波,经椭圆面反射后集中在肾结石上,将其击碎,实现碎石．该方法具有不开刀、无痛苦、无副损伤、易排除、治疗时间短等优势,临床上得到广泛应用．

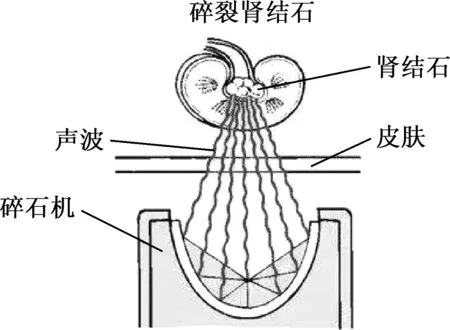
图3

上述两例物理情景不禁让人想起数学上有如下的命题:椭圆上任意一点C,(图2过C点的切线和CA、CB的连线的夹角的角平分线垂直(A、B为该椭圆的两个焦点)

数学方法论证如下:设椭圆方程为

(1)

C(x0,y0)为椭圆上任意一点,过C点作椭圆的切线L,L与CA的夹角为α,与CB的夹角为β,A(-c,0)、B(c,0)为椭圆的左、右焦点．

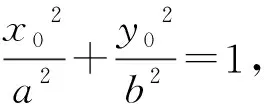
(2)

如果L的斜率存在,设L的斜率为k,则L的方程为

y=k(x-x0)+y0.

(3)

把(3)式代入(1)式得

b2x2+a2[kx+(y0-kx0)]2=a2b2.

即

(b2+a2k2)x2+2a2k(y0-kx0)x+a2(y0-kx0)2-a2b2=0.

因为L为切线,故Δ=[2a2k(y0-kx0)]2-4a2(b2+a2k2)[(y0-kx0)2-b2]=0.

化简得

(a2-x02)k2+2kx0y0+b2-y02=0.

(4)

把(2)式代入(4)式得

上述过程求过C点的椭圆的切线的斜率,非常繁琐,如果用高等数学则过程大大的简化.

对x求导

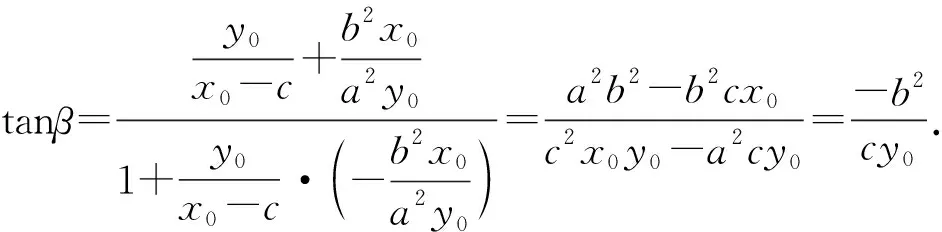
CE是∠ACB的角平分线,∠ACE=∠BCE,α=β,

∠ACE+α+∠BCE+β=180°，

∠ACE+α=90°，CE⊥L.

物理学发展的历史上,通过类比,指引未知领域的研究屡见不鲜,牛顿引力理论加速了库仑定律的发现就是一例.著名的库仑扭秤为了探索电作用力与距离的关系而发明的,扭秤的精致和巧妙设计受到科学史家的普遍关注,可事实上,库仑脑子里早已有了电作用力与距离平方成反比的思想框架,设计扭秤实验只是为了印证这一想法．联想、类比既可以是学科内的,也是可以跨越学科界限的,它是我们认识未知世界的一种重要的工具．