悬挂重物轻弹簧下落过程中的疑惑和解答
曹晓亮 邱为钢
(1. 湖州市吴兴高级中学,浙江 湖州 313000; 2. 湖州师范学院求真学院,浙江 湖州 313000)
中学物理弹簧模型习题中,有这样一道有争议的题目,如文献[1-2]所述:弹簧的一端悬挂一物体,另一端用手固定,则放手的瞬间物体的加速度是多少?此题甚至还作为1987年广东物理高考选择题之一.有争议的答案是这两个,一个认为放手瞬间物体的加速度是0,另一个认为放手瞬间物体的加速度是重力加速度g. 从能量角度考虑,文献[3-4]认为,放手瞬间,弹簧瞬间恢复原状,消失的弹性势能去哪里了?以上疑惑的根本原因是文献[5]所归纳的中学物理弹簧模型,默认为是质量为零的轻弹簧,只存在于习题和考题中.实际轻弹簧是文献[6]中有质量软塑料弹簧(魔力弹簧或彩虹圈),恢复原长是需要时间的,不可能瞬时改变.
对于有争议物理模型问题,最简单实在的方法就是真的去做一下这个实验,用现象和数据说话.实验器材是彩虹圈,网球,纸和手机.用胶带纸把网球黏贴在弹簧的下端,墙面贴一个有长度刻度的纸,用于标记和测量彩虹圈下落距离.用最新款手机的高速摄像功能拍摄,然后导出到电脑中.用视频编辑软件一帧一帧截取下落过程的图像,然后并排叠放,得到图像如图1所示.
从图1可以看出,弹簧并不是瞬时恢复原长的,需要一段时间.在起始下落过程中,下端及网球保持不动.弹簧分为上下两部分,之前下面部分是不动的,上面部分作为一个整体在下落.上端几乎在一条直线上,如图1中的实线所示,这说明上端是匀速下落的. 图1中每幅图间隔20 ms,背景是画有刻度贴在墙壁上的白纸.由图1中的刻度和标记,得到每张图中弹簧上端下降距离与时间的关系,如表1所示.

图1 悬挂网球塑料弹簧的下落

表1
由表1数据,线性拟合得到本实验中弹簧上端下落速度是7.06 m/s. 那么这个下落速度有没有解析表达式?依赖于哪些物理量?
这个问题的理论解答需要比较高深的理论物理知识,故本文只介绍主要思路和结果.设弹簧在原长时,质量随长度是均匀分布的,按文献[7]的做法,设弹簧弹性系数为k,原长为l0,质量为m0.下端悬挂一个质量为m的物体.弹簧的下落过程其实是弹簧在重力场中形变的恢复过程,是重力场中弹簧的波动方程.弹簧形变满足一定的初始和边界条件,用分离变量法或者拉普拉斯变换法求解这个二阶偏微分方程,再利用复变函数中的围道积分和留数定理,理论上可以证明:在下落过程中,弹簧下端保持不动,上端匀速下落,速度是[8]
(1)
其中lg是弹簧不挂重物,在自身重力作用下自然伸长后的总长度.式(1)并不出现弹簧的弹性系数,容易测量和检验.
图1中的实验数据是,弹簧原长6 cm,在重力作用下自身伸长后总长度是30 cm.弹簧质量是24.10 g,网球质量是55.53 g.由式(1),弹簧上端下落速度理论上是7.16 m/s. 考虑到实际弹簧下落过程中有阻力,碰撞,晃动等能量损耗,实际下落速度7.06 m/s应该小于理论速度7.16 m/s.
如果弹簧的质量m0趋向于0,考虑到只在自身重力作用下静止弹簧伸长有以下表达式
(2)
把(2)式代入(1)式,弹簧上端下落速度是这样趋向无穷大的:
(3)
与弹簧质量开根号成反比.弹簧悬挂重物后的伸长量有以下表达式
(4)
恢复形变(下落)时间就是(4)式中的距离比上(3)式中的下落速度
(5)
当弹簧的质量m0趋向于0时,恢复形变(下落)时间这样趋向于0的:
(6)
与弹簧质量开根号成正比.即弹簧质量越小,恢复形变时间也越小,但不是瞬时的.
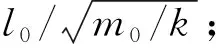
回到原题,如果弹簧是真实的弹簧,那么弹簧下落是需要时间的.放手的瞬间,弹簧最下端不知道上端发生了什么,保持原状,所以物体还是静止,加速度为0.文献[1]的结论是正确的.如是理想的轻弹簧,即弹簧质量趋向于0,可以讨论的比文献[2]更细致.看这个“瞬时”与(6)式的下落时间相比,如比(6)式小,物体静止,加速度为0;如比(6)式大,物体加速度有可能为g.
再从能量角度看,下落过程中重物不动,能量只在弹簧内部相互转换,弹簧减小的重力势能和弹性势能转化为运动下落部分的动能,并没有凭空消失.估算一下这个动能,正比于弹簧的质量与弹簧下落速率的平方,由(3)式可以估计这个动能的近似表达式
(7)
当弹簧质量m0趋向于0时,弹簧动能趋向为
(8)
这个动能是个有限值,并不为0,不会消失.这解决了文献[3-4]的部分疑惑.
这个问题模型对我们的启示是,如果口头讨论得不到要领,不如亲手做实验一次,来验证各种说法对还是不对.弹簧重物下落模型你如果真的做了,才会发现,还有这么多有趣的物理.这个模型不应该出现在试题和考题中,最适合的地方是IYPT或者CUPT等中学生物理锦标赛.本文中的详细理论推导,会在参考文献[8]中查到,有兴趣的读者到时可以验证一下.

