基于RSF信号的高频雷达重构性能分析
吕明久, 孙宗良, 杨 军, 杜 雄, 丁 凯
(1. 解放军95980部队, 湖北襄阳 441000; 2. 空军预警学院, 湖北武汉 430019)
0 引言
高频雷达(High Frequency Radar,HFR)作为一种可以对远距离目标观测的新体制雷达,已成为现代战略预警体系的重要组成部分。然而,由于HFR大多工作于高频频段,其复杂的外界干扰条件,对雷达工作频率的选择、发射带宽的提升等带来了诸多困难。将随机步进频率信号与HFR相结合,通过发射一串载频跳变的子脉冲来避开干扰频段,可以显著增强信号的抗干扰性能,同时实现大的合成带宽,已经得到广泛关注[1-2]。
由于HFR工作环境特点以及RSF信号距离旁瓣高、处理难度大等问题,因此,当前RSF HFR的研究主要侧重于信号子脉冲在可用频带内非均匀分布或者缺失条件下的波形设计和信号处理方法[3-4]。如文献[5]采用自适应目标回波重建算法,实现了降低RSF信号距离旁瓣的目的。文献[6]通过设计不同频率脉冲出现概率来降低信号稀疏条件下的距离旁瓣。近年来,众多学者将压缩感知(Compressed Sensing,CS)理论与RSF信号相结合,通过利用回波信号的稀疏信息,获得了信号随机、稀疏条件下的高精度重构结果[7]。文献[8-9]基于CS理论实现了信号子脉冲缺失条件下的HFR距离-多普勒二维高分辨重构。然而,当前基于CS理论的RSF HFR均只考虑了如何快速实现回波信号的快速、精确重构,而对于RSF信号的发射子脉冲个数、子脉冲带宽大小等对重构性能的影响涉及较少。实际上,由于HFR工作频带的非均匀分布,在相同的合成带宽条件下,设置不同的RSF信号发射参数(子脉冲个数、载频跳变方式等)将会对最终稀疏重构结果产生影响,因此具有十分重要的研究价值。
针对上述问题,本文对基于CS理论的RSF HFR稀疏重构性能进行了研究。首先构建了RSF HFR二维稀疏重构模型。其次,利用感知矩阵性能作为衡量指标,推导出影响感知矩阵互相关性能(最大互相关系数、平均互相关系数)的信号参数,得出在相同合成带宽条件下,采用子脉冲随机步进方式、增加发射子脉冲个数的方式可以得到更好的RSF HFR二维稀疏重构结果。最终,利用仿真实验对上述结论进行了验证。本文的研究对RSF HFR的波形设计以及提升基于CS理论的稀疏重构性能分析具有重要的实际意义与作用。
1 RSF HFR二维稀疏重构模型
RSF信号的数学模型可以表示为[9]
(1)
式中,μ1(t)为子脉冲复包络,Tr为脉冲重复周期,N为子脉冲个数,fn为第n个子脉冲的载频,可以表示为
fn=fc+ΓnΔf
(2)
式中,Γn∈[0,N-1]且|Γn|=N,|·|表示集合的势,即包含的元素个数,fc为初始载频。
如图1所示,HFR的工作频段中存在大量的外界干扰,很难找到一段较大且连续干净的“寂静”频带。而通过选择合适的RSF信号子脉冲载频以及发射个数可以实现大的合成带宽。假设用矩阵Φ表示信号随机发射的规律,则RSF信号发射规律可以表示为
ΓN×1=ΦN×NΠN×1
(3)
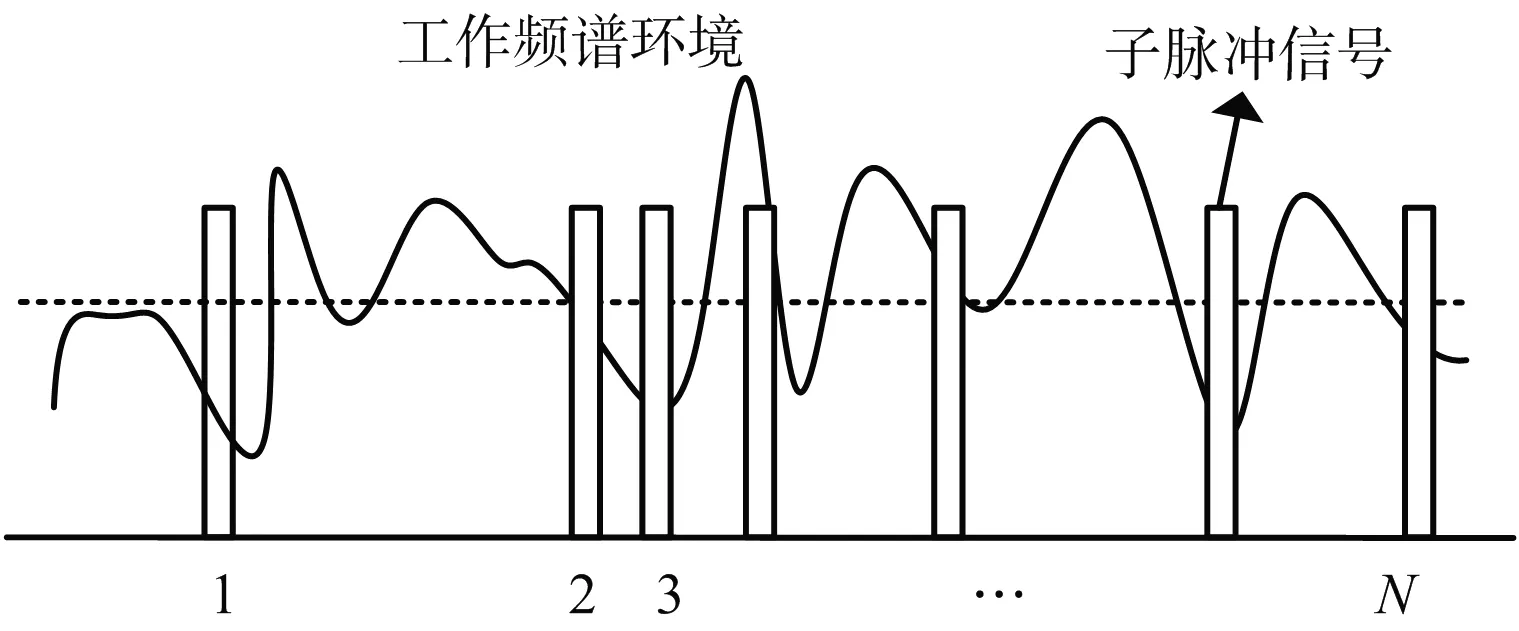
图1 HFR工作环境示意图
式中,Π=[0,1,…,N-1],矩阵ΦN×N={φi,i′}的构造方式可以写成:
φi,i′=1,i′=i
(4)
假设只发射M(M≤N)个子脉冲信号,此时可视为从fn中随机抽取M个频点参与重构,可以通过式(3)所示的量测矩阵Φ对子脉冲载频fn进行选择。
此时,对于一个脉组内的回波采样信号可以写成[9]:
(5)
当目标与雷达之间存在相对运动时,为简化分析,此处假设目标只存在匀速运动,此时τk可以表示为
(6)
式中,Rk为第k个散射点与雷达的初始距离,V为目标径向速度。
在距离、多普勒二维空间中,观测目标只占少量的部分,因此可以视为稀疏的。根据CS理论,可以将目标在距离域划分为[R1,R2,…,RP]个网格,在速度域划分为[V1,V2,…,VQ]个网格,因此可得到一个P×Q维的目标场景矩阵X(p,q)。此时式(5)可以表示为
(7)
式中,
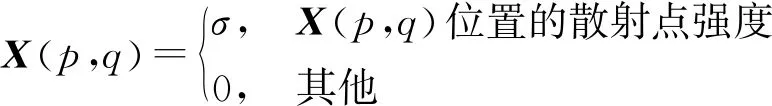
(8)
将式(7)写成矩阵形式可以得到:
u=Θx+W′
(9)
其中u=[U1,…,Un,…,UN]T,x=[X1,X2,…,XPQ]T为X(p,q)行列堆叠的结果,矩阵Θ中的元素可以表示为
h(n,(p-1)Q+q)=
(10)
因此,Θ为N×PQ,(N≪PQ)维矩阵且可以表示为
Θ={h1,…,hpQ+q,…hPQ}
(11)
式中,hi为维度为N×1的向量,W′为噪声向量。
上述过程完成了RSF HFR稀疏重构模型的建模,下面基于上述模型对不同参数条件下的稀疏重构性能进行分析。
2 稀疏重构性能衡量方法
2.1 感知矩阵互相关性
对于上述基于CS的RSF HFR稀疏重构模型,Donoho等人提出了感知矩阵Θ的非相关性约束条件,通过定义感知矩阵Θ中各列之间的最大互相关系数来定量描述。Θ各列的最大互相关系数μmax定义为[10]
(12)
式中,Θi表示矩阵Θ的第i列,〈·,·〉表示内积。
由于最大互相关系数μmax只描述了感知矩阵Θ的局部互相关特征,为此,文献[12]提出了感知矩阵Θ平均互相关系数的概念,矩阵Θ的平均互相关系数μave定义为
(13)
式中,κ∈[0,1],当κ=0时,μave为Gram矩阵G中非对角线元素和的均值。当平均互相关系数μave较小时,表明Θ的整体相关性较弱,稀疏重构的性能将越好。
在当前的文献中,采用最大互相关系数μmax与平均互相关系数μave的稀疏重构性能优劣评判方法(即当μmax越小时,稀疏重构性能越好;当μmax相等时,μave越小,对应的稀疏重构性能更优)已经得到学者的认同,并得到了广泛使用[13]。因此本文利用μmax以及μave作为评价指标,分析RSF HFR稀疏重构性能。
2.2 RSF HFR感知矩阵互相关性表征
结合式(9),RSF信号其感知矩阵Θ的第i列与第j列的互相关系数μi,j可以表示为
(14)
此时感知矩阵Θ的最大互相关系数为
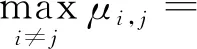
(15)
同理,通过式(14),当κ=0时,感知矩阵Θ的平均互相关系数μave可以表示为
(16)
从式(15)、式(16)可以看出,μmax以及μave大小与RSF信号子脉冲个数、载频步进方式等因素有关。假设RSF信号的合成带宽为250 kHz,载频f0=10 MHz,子脉冲重复频率PRF=3 000 Hz,分别设置子脉冲个数为N=50,100,150,对应的子脉冲带宽分别为Δf=5,2.5,5/3 kHz。假设距离域、速度域离散点数相等,即P=Q=N。图2中所示为随机选取M=0.8N个子脉冲参与重构时,相应的感知矩阵互相关系数大小统计直方图(上述结果均为500次蒙特卡罗统计的均值,且图中以0.02为统计间隔,下同),相应的最大互相关系数和平均互相关系数如表1所示。为便于比较,图中给出了顺序步进(Linear Stepped Frequency,LSF)信号的统计结果。
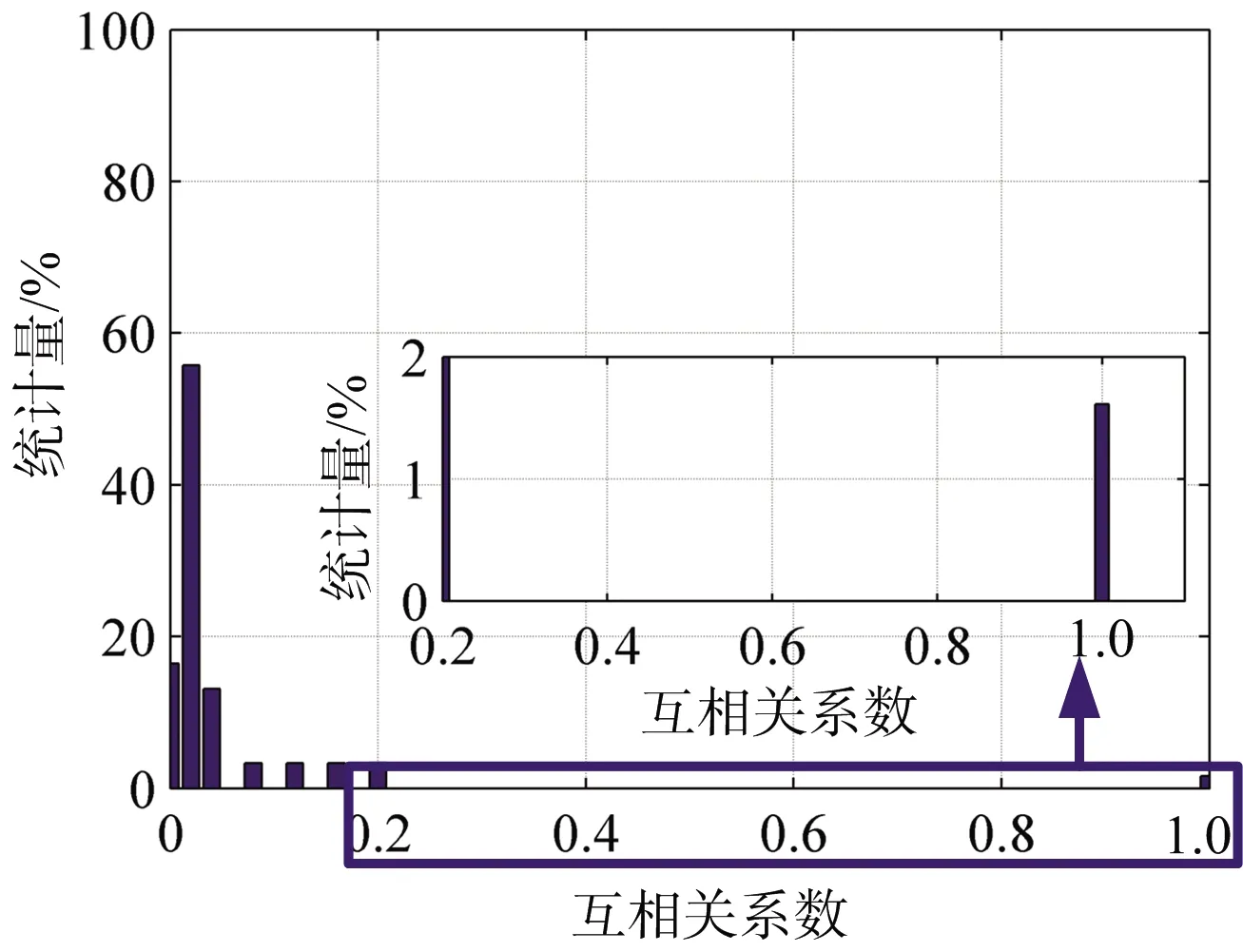
(a) N=50时LSF信号

(b) N=50时RSF信号
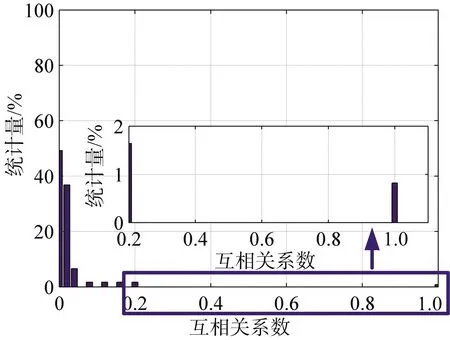
(c) N=100时LSF信号

(d) N=100时RSF信号
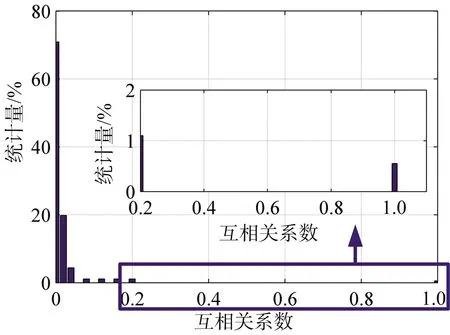
(e) N=150时LSF信号

(f) N=150时RSF信号

表1 相同合成带宽条件下最大互相关系数与平均互相关系数
从图2以及表1的对比可以看出:对于LSF信号,不论子脉冲个数如何变化,其对应的最大互相关系数始终为1,但是平均互相关系数随着子脉冲个数变少而逐渐变大。对于RSF信号,平均互相关系数与最大互相关系数均随着子脉冲个数的减少逐渐增大。在相同的条件下,LSF信号的最大互相关系数始终大于RSF信号的最大互相关系数。综上所述,基于CS的RSF HFR二维稀疏重构性能可以总结为:
1) 在相同的合成带宽条件下,选择较多的发射子脉冲个数可以降低感知矩阵最大互相关系数以及平均互相关系数,能够得到较好的稀疏重构结果。
2) 子脉冲载频采用随机步进的方式可以得到更小的感知矩阵最大互相关系数,更有利于信号的稀疏重构。
3 仿真分析与验证

仿真1 不同步进方式条件下二维稀疏重构性能
依据上节信号参数并假设子脉冲个数N=50,距离域、速度域离散点数均设置为50,即M=N。图3为在不同稀疏度K条件下LSF信号与RSF信号的稀疏重构误差比较,蒙特卡洛仿真次数同样设置为500次。
从图3可以看出,在不同的稀疏度条件下,载频随机步进比载频顺序步进信号的稀疏重构误差小,这与图1中RSF信号对应的感知矩阵最大互相关系数小于LSF信号对应的感知矩阵最大互相关系数的结论一致。

(a) 稀疏度为8
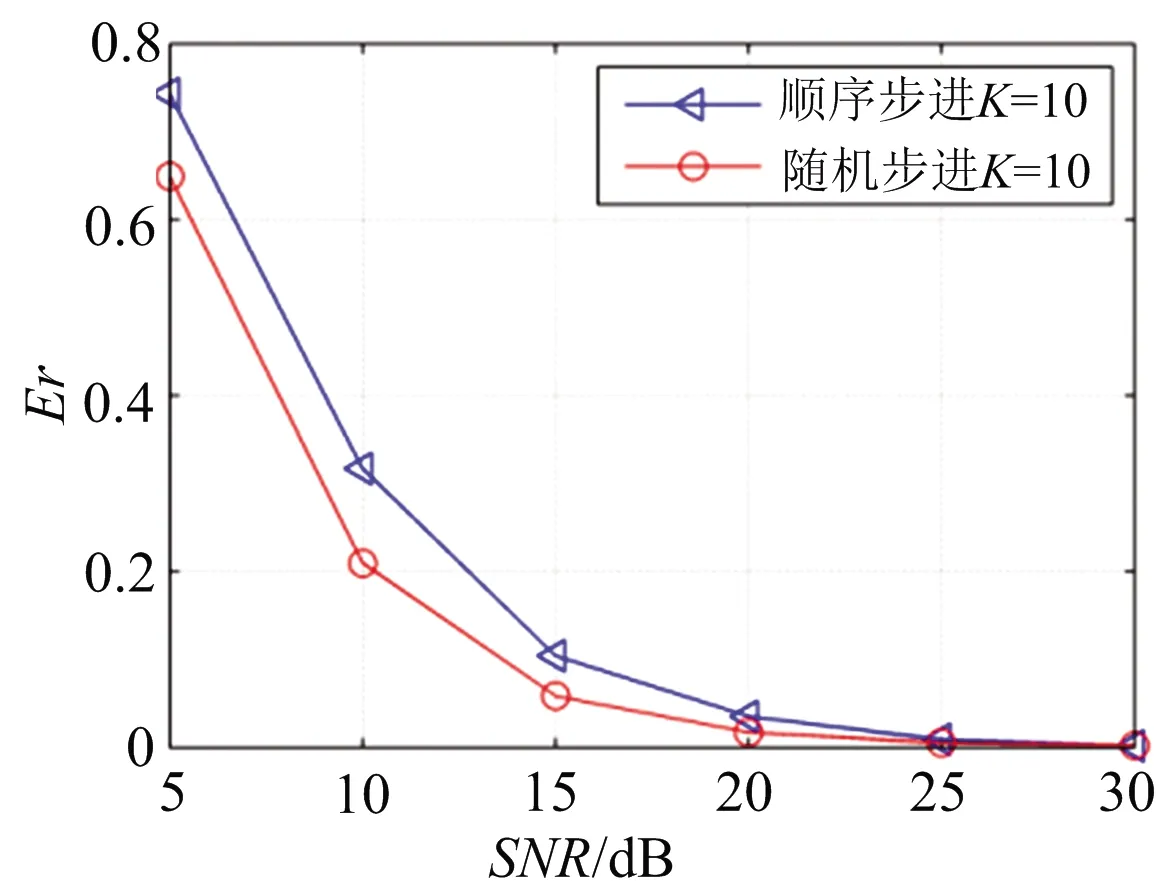
(b) 稀疏度为10
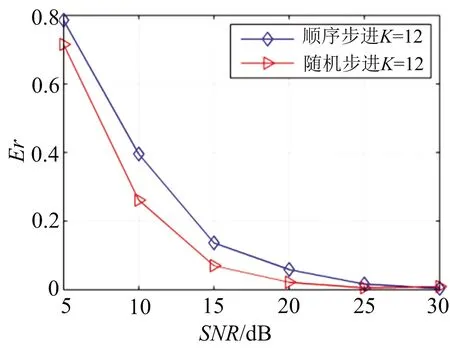
(c) 稀疏度为12
为进一步验证上述结论,假设信噪比为15 dB,设置如图4所示的距离、速度二维待重构结果(稀疏度为8)。图5分别为载频顺序跳变以及载频随机跳变的步进频率信号稀疏重构结果。
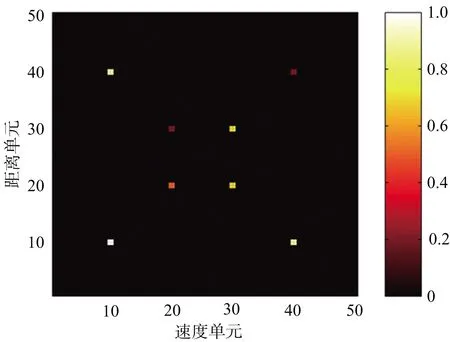
图4 原始二维图像
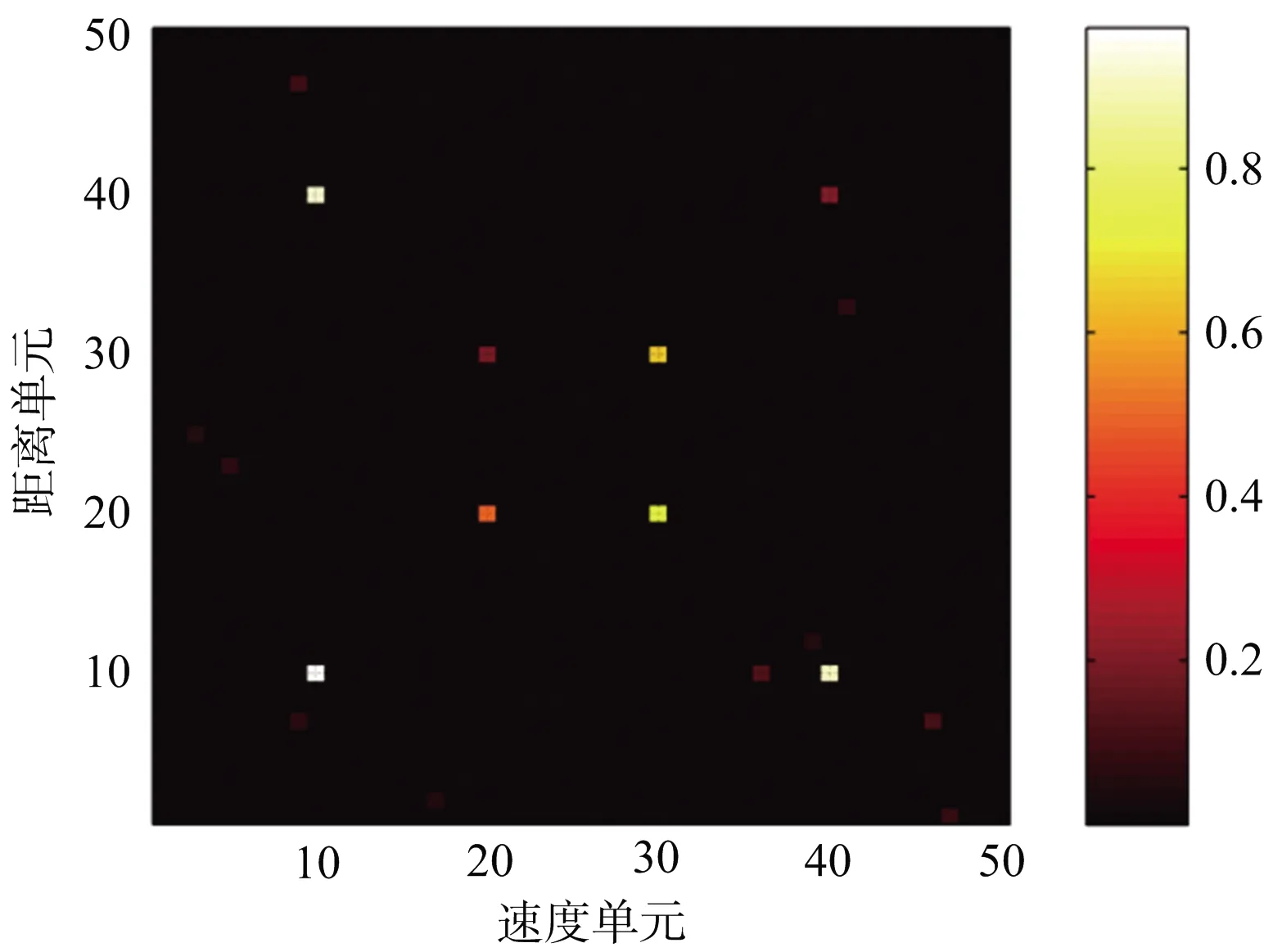
(a) LSF信号重构结果

(b) RSF信号重构结果
从图5的二维重构结果可以看出,当载频顺序变化时,原始图像中出现了较多的虚假重构点,而当载频随机跳变时,虚假重构点明显小于载频顺序步进时的结果,因此具有更好的稀疏重构性能,从而进一步验证了上述结论的正确性。
仿真2 不同子脉冲个数条件下二维稀疏重构性能
假设参数设置条件不变,信噪比为10 dB,图6为相同合成带宽条件下,子脉冲个数分别为100和150时RSF信号的稀疏重构结果。

(a) N=100时重构结果

(b) N=150时重构结果
从图6可以看出,当子脉冲个数为150时,二维稀疏重构效果要好于子脉冲为100时的重构结果。这是由于在相同的合成带宽情况下,子脉冲个数越多,感知矩阵最大互相关系数越小,因而稀疏重构效果越好。
假设条件不变,图7为稀疏度为8时,LSF信号与RSF信号在不同的子脉冲个数条件下的稀疏重构性能对比,蒙特卡罗次数为500次。
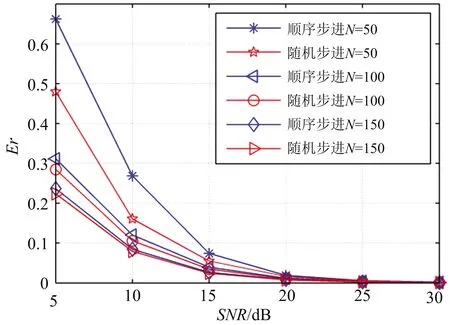
图7 不同条件下重构性能对比
从图7可以看出,对于上述两种载频步进规律不同的信号,子脉冲个数越多,信号的稀疏重构性能越好。另外,从上述仿真还可以看出,在相同的子脉冲个数条件下,随机步进信号的重构误差始终小于LSF信号的稀疏重构误差,这也进一步验证了上一节感知矩阵互相关性结论的正确性。
4 结束语
本文构建了RSF HFR二维稀疏重构模型,并基于此对影响RSF HFR二维稀疏重构性能的因素进行了分析,得出在合成带宽一定的条件下,设计载频随机步进、子脉冲个数越多的RSF信号可以得到更好的稀疏重构性能的结论。文中的研究结论对于未来HFR的波形设计指明了一种可行的技术方向。

