球载雷达地杂波建模与仿真分析
宿文涛, 刘润华, 汪 枫
(空军预警学院, 湖北武汉 430019)
0 引言
随着技术的发展,各种新体制的雷达蓬勃发展,与其他类型的雷达相比,球载雷达在对重点空域的长时间持续监控、应对低空超低空突防、处理城市内的不明空情等方面具有独特的优势[1]。球载雷达一般部署在较高的空中,覆盖范围远超常规的地基雷达,同时也是应对威胁越来越大的无人机等低慢小目标的有效手段[2]。
球载雷达采用波束下视的方式工作,所以其面临的地杂波较强,与机载雷达[3-4]相比,球载雷达平台处于系留状态,运动幅度较小,由于自身没有动力在空中的运动主要是受到风向与风力的影响,所以雷达回波的主杂波偏移和展宽较小,但是由于风力的随机变化,会给杂波的频率特性带来不确定性,这会给杂波抑制带来麻烦,因此有必要对球载雷达的杂波特性进行研究。地杂波模型已比较成熟[5-6],但是球载雷达的地杂波模型有其独特性,国内在此方面的研究较少,建立的模型趋于理想化,球载雷达的特点体现不明显。本文针对风对球载平台的扰动引起杂波频谱展宽的变化问题进行讨论,采用零记忆非线性变换法对杂波谱特性精确仿真,为进一步了解球载雷达杂波特性,研究相应的杂波抑制技术提供了参考。
1 球载雷达杂波的空间模型
球载雷达一般部署在远小于地球半径的3~5 km的高空处,可以认为每个地面分辨单元是一个平面,在波束照射大范围区域内可以认为有无限个散射体,对此一般采用网格映像法[7]实现地面分布式杂波信号模拟。图1中以球载雷达地面垂直投影为原点建立直角坐标系,其空间模型如图所示。

图1 球载雷达空间几何模型
1.1 网格单元划分
1) 距离环划分
设球载雷达的信号带宽为B,斜距分辨率ΔR=c/2B,斜距单元在地面的投影为地面距离环的最小划分单元Δr=ΔRsecφ,φ为杂波分辨单元的俯仰角。
中重频模式下,由于存在距离模糊[8],雷达实际接收到的杂波信号是由多个距离环杂波采样叠加而成的。由于同一距离环中杂波分辨单元有相同的高低角,这些杂波距离环就是一簇同心圆环,如图1中的等距离圆弧所示,每个杂波距离环的距离宽度取决于距离门宽度及该距离环对应的高低角。距离模糊环数的计算公式如下:
(1)
2) 方位角间隔划分
方位角的划分取决于方位角的角度分辨率,雷达的多普勒分辨率确定角度分辨率,一般为了满足最小分辨率和合适的计算量,方位角划分间隔一般选取为
(2)
式中,λ为雷达波长,N为一个CPI(相干处理时间间隔)的脉冲积累个数,v为平均风速即雷达平台的平均速度。
1.2 平台扰动
系留气球空中姿态简示图如图2所示。考虑球载平台的特殊性,建立简单的球载平台空中姿态模型[9-10]。在此将球载平台称为浮空器,升空方式为自由升空,当浮空器到达预定位置后,系留缆绳被拉直,浮空器悬停在高空。只考虑系留缆绳的拉力,浮空器的重力及空中风力的影响。忽略浮空器的升空过程,仅讨论浮空器在空中的姿态问题。

图2 系留气球空中姿态简示图
假设空中风分为连续的稳定风和离散的突变风两部分,球载雷达平台在空中会受到风吹的影响,稳定风会导致平台缓慢飘动,突发风是冲击型,短暂作用平台,然后平台恢复正常,这会导致平台上下俯仰。
浮空器的空中姿态主要分为两种类型:
1) 浮空器在理想情况下即无风或者连续风状态下,浮空器静止在空间一点,振动幅度非常小,可以忽略不计;无风状态下的平衡位置在初始升空点的上空,在连续风情况下,浮空器的平衡位置会沿风向有一定的偏移,偏移量随风速的增大而增大。
2) 浮空器在突变风的情况下,会在某一小范围空域内震荡,震荡情况随风速的变化而变化。浮空器的俯仰角随时间的变化情况如图3所示。

图3 浮空器的俯仰角随时间的变化情况
由突发风引起的平台上下俯仰可以看成雷达在俯仰向做一定速率的扫描,进而引起杂波频谱的展宽。注意突发风在时间上是离散冲击型,所以在一段时间来看,球载雷达在俯仰上的扫描不是均匀的,有突变风时杂波的谱宽会较大,没有突变风时杂波的谱宽较小。表1给出几种风速下的转化为俯仰向扫描速率的典型值。

表1 几种情况下俯仰向扫描速率转化值
2 球载雷达杂波建模
2.1 球载雷达二维地杂波数学模型
对于脉冲多普勒体制的球载雷达,一个CPI有N个脉冲,每个脉冲有M个距离门,目的就是建立N个脉冲的杂波回波数据使其尽可能的接近真实的杂波情况。某个数据单元的杂波信号由两部分组成,一部分是距离环上所有的方位分辨单元信号的叠加,另一部分是由于工作在中重频模式下的球载雷达会存在距离模糊,一个距离门的杂波回波由多个模糊的距离环叠加。因此首先要计算所有杂波单元的信号,然后进行两次叠加得到某一数据单元的杂波信号。
设Cn(i,j)表示第n个脉冲对第i个距离环第j个方位分辨单元的采样杂波数据(忽略了噪声项),则有
Cn(i,j)=AijPijexp(jφn)
(3)
式中,Aij表示杂波的统计特性分布,Pij表示杂波功率,φn表示球载雷达运动引起的相位调制。
φn=2πfd(n-1)Tr
(4)
式中,Tr为脉冲重复周期,fd=(2v/λ)·cosφij表示该分辨单元的多普勒频率。
对第i个距离环上所有方位向的分辨单元杂波信号进行叠加后,得到第i个距离环的杂波信号为
(5)

2.2 杂波的统计特性及数据产生
地杂波是一种面杂波,地面上的物体如草、木、庄稼等会随风摆动,造成地杂波大小的起伏变化,这种随机起伏特性可以用PDF(概率密度函数)表示,常用的统计模型有瑞利分布、对数-正态分布、韦布尔分布和K分布等,因为地杂波是由天线波束照射的大量散射单元回波合成的结果,一般可以用韦布尔分布精确描述。其表达式[11]为
(6)
式中,c为尺度参数,v为形状参数。
地杂波可以看成一种随机过程,除了PDF外,还必须考虑其相关特性。通常地杂波的功率谱可以采用高斯模型表示,成为高斯谱,表达式为
(7)
式中:fd为地杂波的频谱偏移,在式(4)中已经体现,不再讨论;σc为地杂波的标准差,代表频谱的展宽程度。有
(8)
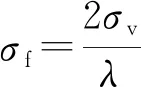
例如波长为0.1 m,天线转速为6 r/min,θ3=2°,稳定风为20 m/s,伴随10 m/s的离散突风,表2给出了典型情况下的地杂波标准差。

表2 球载雷达典型情况下地杂波的标准差
数学模型中的Aij体现杂波的统计特性,针对以上的分析,对于球载雷达地杂波的模拟需要同时满足功率谱分布和幅度分布,在这里采用零记忆非线性变换[14](ZMNL)产生满足要求的序列,ZMNL算法是用相关的高斯随机过程经过某种非线性变换来得到所需的相关随机过程,该方法比较经典,思路清晰且计算量小,可以形成快速算法。ZMNL法的基本原理框图如图4所示,首先由功率谱为1的高斯白噪声序列vi,i=1,2, 3,…,N,通过一线性滤波器H(ω)产生相关高斯随机序列wi,i=1,2, 3,…,N,使wi各个时间点上的随机变量满足某种相关性(功率谱);然后经过非线性变化g(·)得到需要的相关非高斯随机序列zi,i=1,2,3,…,N,即为所需杂波。通过此过程得到了Aij。

图4 ZMNL法原理框图
2.3 杂波的功率
对于球载雷达环境,存在天线旁瓣波束近似垂直入射形成的高度线杂波,同时考虑不同地形的散射特性,杂波后向散射系数采用常用的Morchin模型,其表达式为

(9)
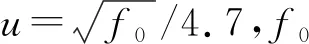

表3 地杂波Morchin模型参数表
可以计算出一个杂波单元的面积Ac≈RΔRθ3secφ,则σ=Acσ0。
由雷达方程可以得到某个单元的杂波功率
(10)
式中:L为球载雷达的综合性损耗;Gij=G0F2(i,j),G0为天线最大功率增益,F(i,j)为天线的方向性函数。
3 仿真结果与分析
为验证模型的有效性、设置仿真实验并进行分析,下面进行一个观测平坦均匀地杂波的下视球载雷达的距离杂波谱仿真,仿真参数设置如下:球载雷达高度H=3 000 m;脉冲重复频率PRF=3 000 Hz;则最大不模糊距离为50 km,最小探测距离为3 km,所以仿真距离为3~50 km;载频f0=3 GHz;雷达最大天线增益G0=35.6 dB;发射功率Pt=20 kW;天线俯仰波束宽度θ3=10°;天线水平波束宽度φ3=1.8°;LFM信号带宽B=2 MHz;波长λ=c/f0=0.1 m;脉冲宽度τ=20 μs;稳定风速即雷达相对地面速度v=20 m/s,伴随有突变风,相干处理脉冲长度N=64;杂波分辨单元初始方位角θ=0°;杂波分辨单元初始俯仰角φ=10°,杂波统计特性为幅度服从韦布尔分布,功率谱服从高斯分布。仿真步骤如下:
1) 序列Aij的产生,首先利用ZMNL法产生N×M维的序列,N为脉冲数,M为距离单元数,韦布尔分布的参数取值为p=2,c=0.5,功率谱参数σc=15 Hz。
图5给出了Aij的产生过程,图5(a)表示首先产生独立不相关的高斯序列,然后生成韦布尔序列如图5(b),最终产生的序列幅度服从韦布尔分布,功率谱服从高斯分布如图5(c)、(d)所示。由于风情的不同,功率谱会发生变化,图6给出了只有稳定风(σc=15 Hz)和稳定风加突发风(σc=30 Hz)两种情况下的结果。
2) 根据式(10)计算每个杂波单元的功率Pij。
3) 根据式(3)得出每个杂波单元的采样数据Cn(i,j)。

图5 杂波序列产生过程
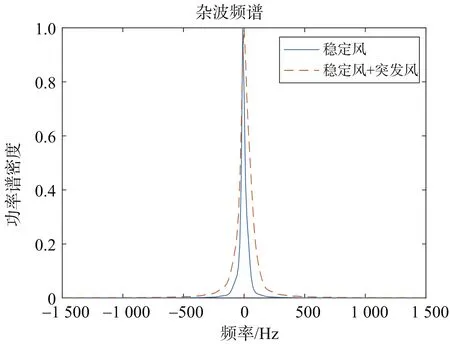
图6 不同情况下杂波频谱对比
图7(a)、(b)给出了64脉冲的距离多普勒谱仿真,为了便于观察图8给出了二维视角,容易看出主瓣杂波(400 Hz处),最短距离的杂波出现在0 Hz左右和3 km处,这是相对较强的高度线杂波,虽然球载平台移动速度较慢,但是由于波长较短,其主瓣杂波与高度线杂波依然间隔较大,可以发现在其他更远的距离上,杂波存在一定角度而不是雷达正下方,它们的多普勒频率非零且随距离的变化而变化。
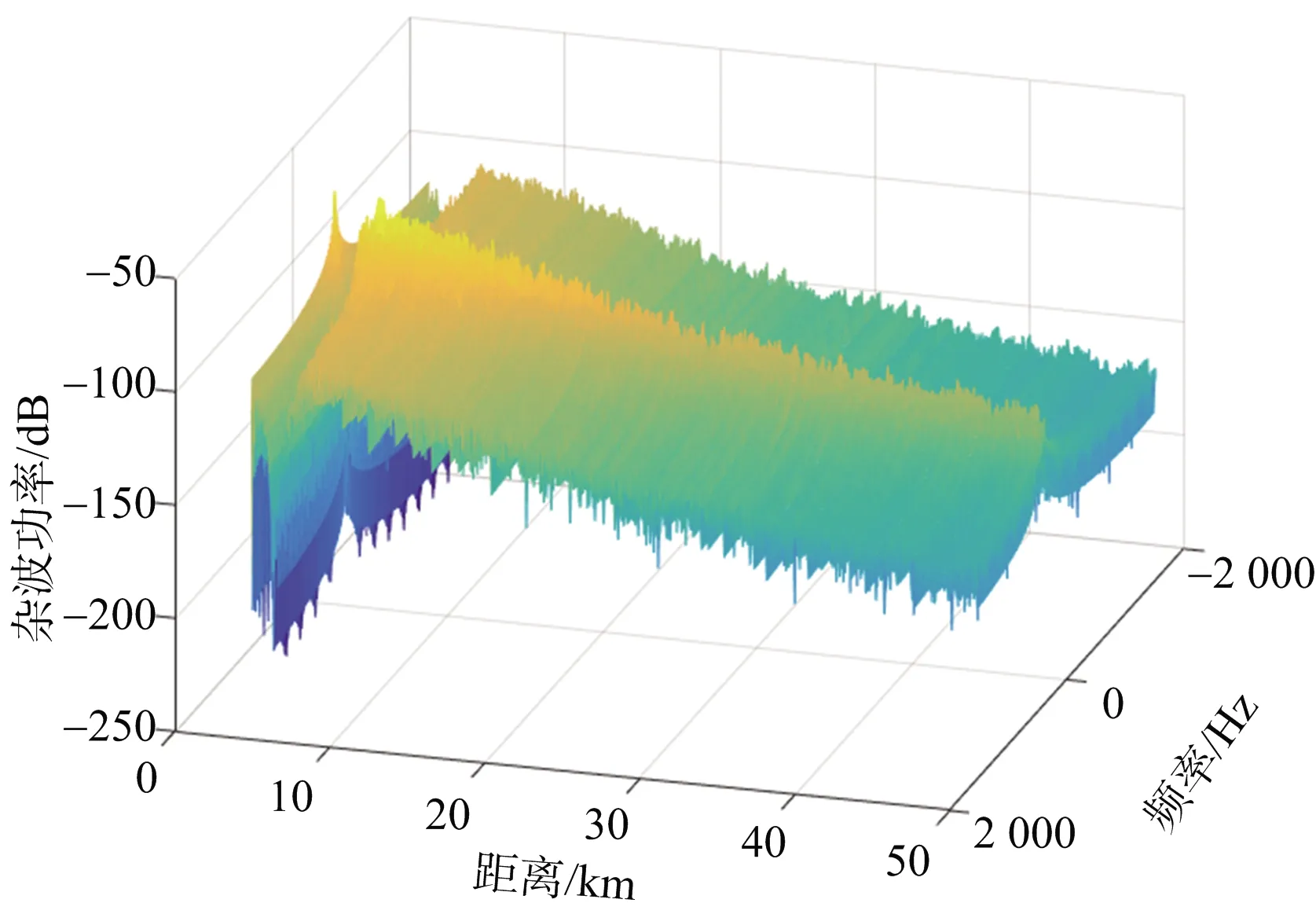
(a) 透视图

(b) 俯视图

图8 多普勒对应的杂波功率(距离向积分)

图9 稳定风下某单元频谱
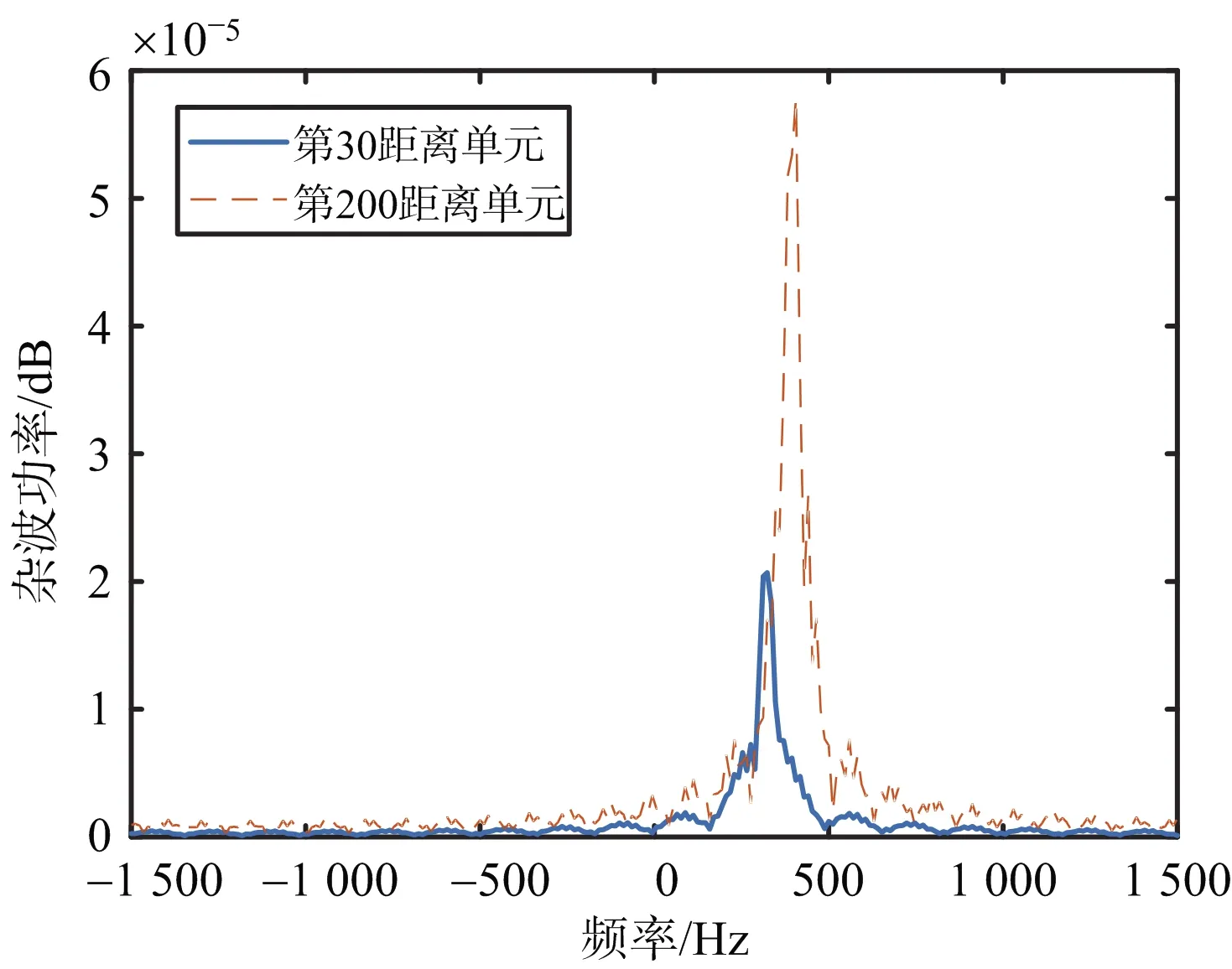
图10 稳定风加突发风下某单元频谱
要清楚地看出不同情况下的杂波功率谱,需看某个距离单元的杂波功率谱,图9、图10分别给出了只有稳定风和稳定风加突发风两种情况下的第30、第200距离单元的杂波功率谱,可以看出只有稳定风的谱宽较窄,稳定风加突发风的谱宽较宽,符合理论分析。
4 结束语
本文建立了球载雷达地杂波模型,并根据这种模型得到了相应的仿真结果。球载雷达杂波具有其独特性,与地基雷达相比,球载雷达波束下视,地杂波强度大,由于平台的移动频谱会有偏移,且展宽也较大。与机载雷达相比,其移动速度较慢,展宽较小,但是由于球载平台没有动力,易受风的影响,运动特性具有随机性,导致其谱宽具有时变性,这对球载雷达的杂波抑制带来的困难。通过分析,对球载雷达的杂波特性和杂波的影响因素有了更深入的认识,有利于以后解决低空小目标难以检测的问题,同时为后续的地杂波抑制方法提供了仿真数据。

