某烹饪器具抽屉结构拉出过程仿真分析与实验验证

周唯儒 莫远忠 朱丽珊 万博臣

珠海格力电器股份有限公司 广东珠海 519070

1 引言

烹饪器具中有一种抽屉结构，这种结构由储物抽屉和外框支撑部件组成。在抽屉底部有一个凹槽，与凹槽相连接的部位是一个凸起的卡扣，卡扣的作用一个是可以定位关闭时候的位置，另一个是在抽屉关闭的时候提供一个向上的弹力，从而辅助抽屉归位，限制抽屉位移并固定抽屉。有了这个结构，即便产品的安装角度不在水平面上，也可以保证抽屉的顺利归位与正常工作。

本文所涉及的卡扣是塑料材料，这种材料具有经济性、柔韧性和注塑可行性。卡扣是简单、快速和经济的连接结构，主要通过卡与扣在装配时的弹性变形和到位后的复原变形实现两个部件的连接和固定。卡扣连接可以实现其连带部件的多次分离和连接而不对产品结构产生影响[1]。

通常仿真分析都会简化模型，处理掉模型细节[2]。目前已经有很多研究人员进行了卡扣的研究工作，模型的处理都进行了简化[3-7]。本文通过使用Ansys Workbench软件进行仿真，分析中没有简化模型，而是直接将原模型进行网格划分处理，尽力保留模型的细节。通过在Ansys Workbench软件中，定义整个拉出时间为10s，两个分析步进行瞬态动力学分析，预测拉出力大小以及卡扣最大应力位置。通过实验结果与仿真结果的对比，得出二者的差异，判定本文中所述的仿真参数可以用于此类产品卡扣设计与分析，从而为相关产品的设计提供一种仿真方法。

2 有限元模型的建立

根据某型号产品结构三维模型，先将模型进行切分，提取需要分析的模型如图1、图2所示。定义图3中红色面和蓝色面为接触面，接触面之间的摩擦类型定义为无摩擦。在Ansys Workbench软件中模拟抽屉由图1所示位置拉出的过程中抽屉和卡扣的应力、变形以及拉出力大小。定义图4中蓝色面为固定约束面，定义图5所示黄色面沿着图示箭头方向（黄色面的法向方向）移动10mm，移动分两步进行，第一步移动0.1s，第二步移动9.9s，用来模拟抽屉拉出的整个过程。对各部件进行网格划分，网格大小为抽屉2mm，框架3mm，划分网格后的单元数量为2191359个，网格模型如图6所示，网格质量如图7所示。

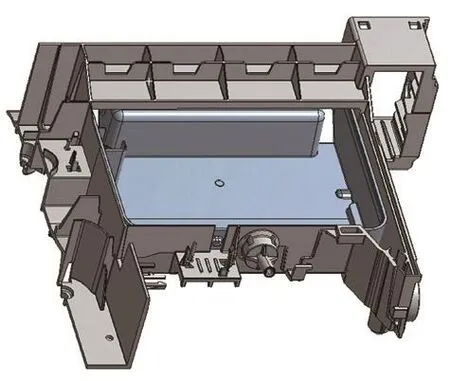
图2 抽屉和固定架模型图2

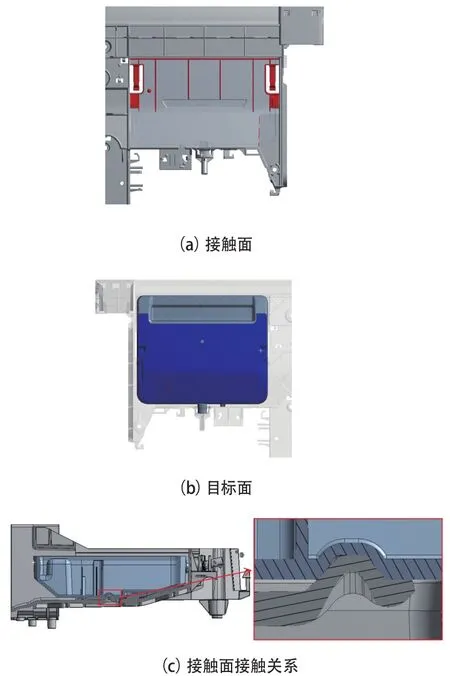
图3 接触面设置

3 求解及材料设定

定义材料参数。抽屉为聚碳酸酯（PC）材料，取弹性模量为2300MPa、泊松比为0.39[5-8]。卡扣为聚酰胺-6（PA6）材料，取弹性模量2000MPa，泊松比为 0.386[9-10]。在求解设定中，定义两步计算，第一步运动0.1s，子步定义为10，使接触平稳的建立。第二步运动9.9s，子步定义30，整个过程模拟用10s的时间拉出抽屉10mm，卡扣被完全压下的过程。设置完毕后导出文件为inp格式文件，提交云服务器进行计算。

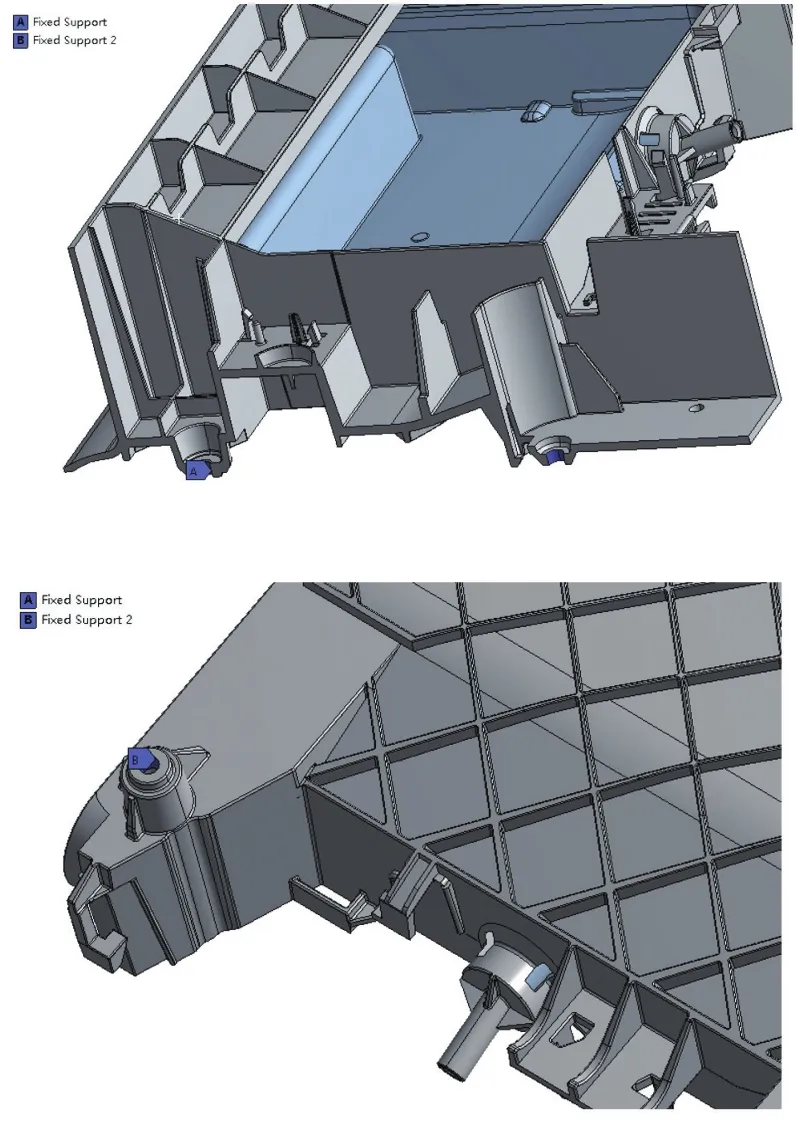
图4 固定约束面设置

4 仿真计算结果

本次仿真模拟了抽屉拉出的过程，为了更好的贴近真实情况，本次分析采用了不简化模型的方法，从而导致了网格数量庞大，一共有2191359个单元，在112个核云计算平台耗费了62.692小时计算完成。虽然计算机计算时间长，但是工程师的前处理时间很短，只用了2小时。

根据所得结果，首先查看变形图。如图8所示，卡扣已经被完全压下，此时整个计算时间是10s，与初始设定的计算时间相同。图9为卡扣在10s时的变形图，从图中可以得出，拉出过程中10s时刻的卡扣的变形最大为2.4989mm，筛选整个拉出过程中的变形数据（如表1所示），在拉出过程中，卡扣的最大变形为2.6256mm，变形方向为坐标系Y轴负方向。整理表1数据可以得到图10所示的曲线图，该图可以直观的表现拉出过程中，拉出时间与卡扣变形的关系。

图11所示为整个拉出过程中卡扣的最大应力情况，根据图中所示结果表明最大应力所处位置为卡扣加强筋根部，靠近卡扣与框架连接部位有39MPa，小于PC材料的屈服强度60MPa，在往复推拉抽屉的时候，此处容易因为应力集中产生开裂或者断裂等破坏现象。

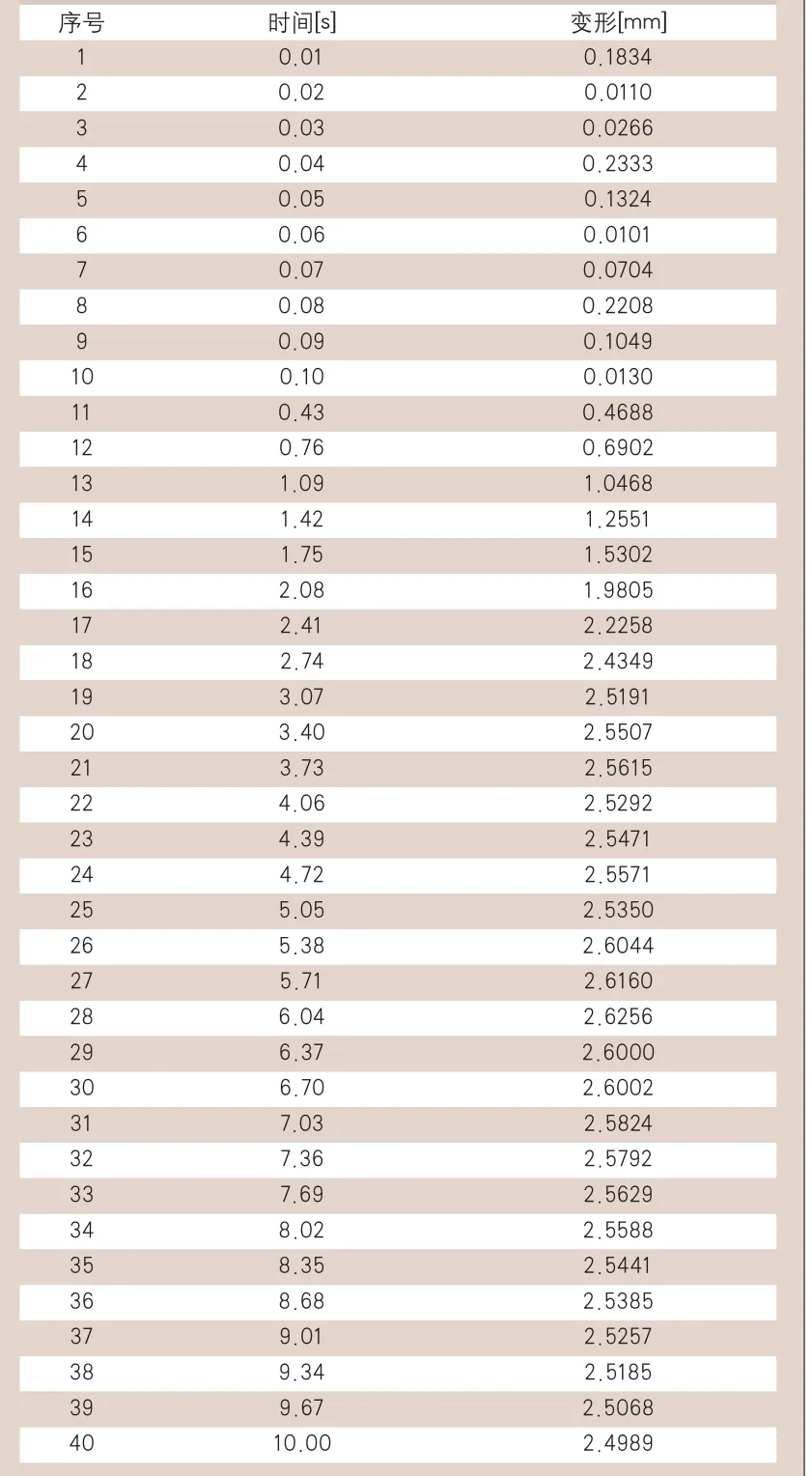
表1 拉出时间与卡扣变形的关系

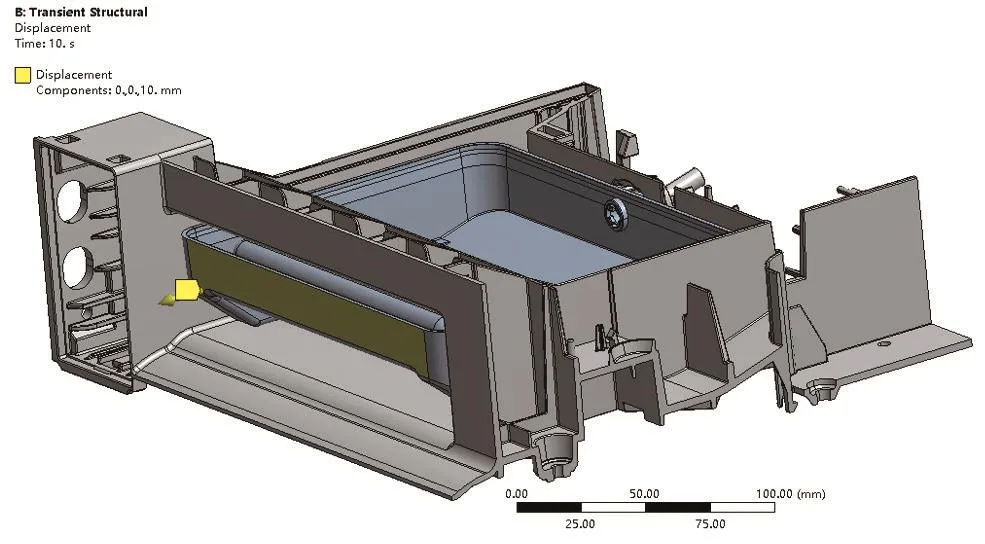
图5 定义位移方向和距离

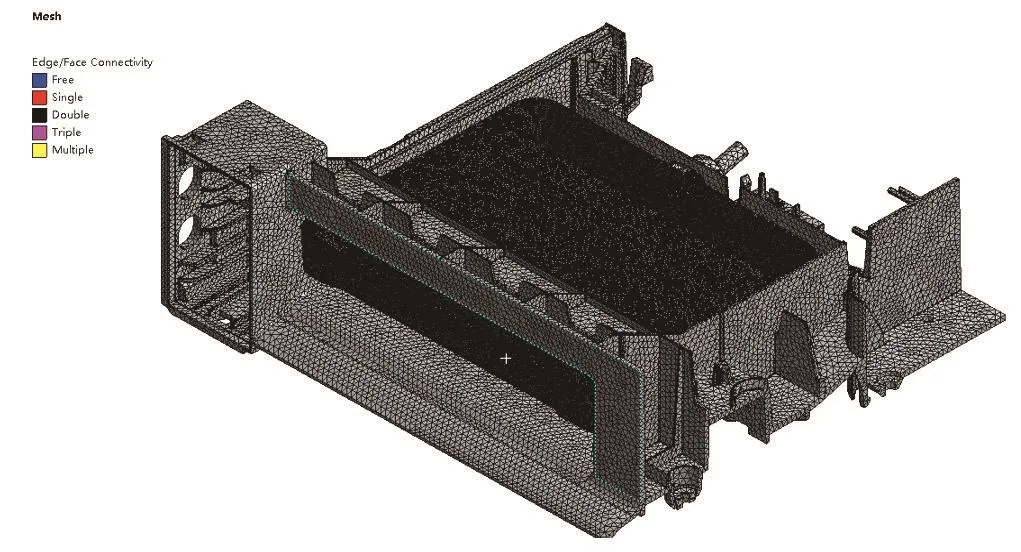
图6 网格模型

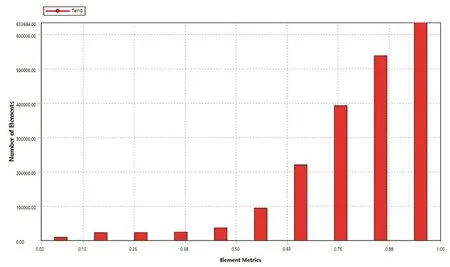
图7 网格质量

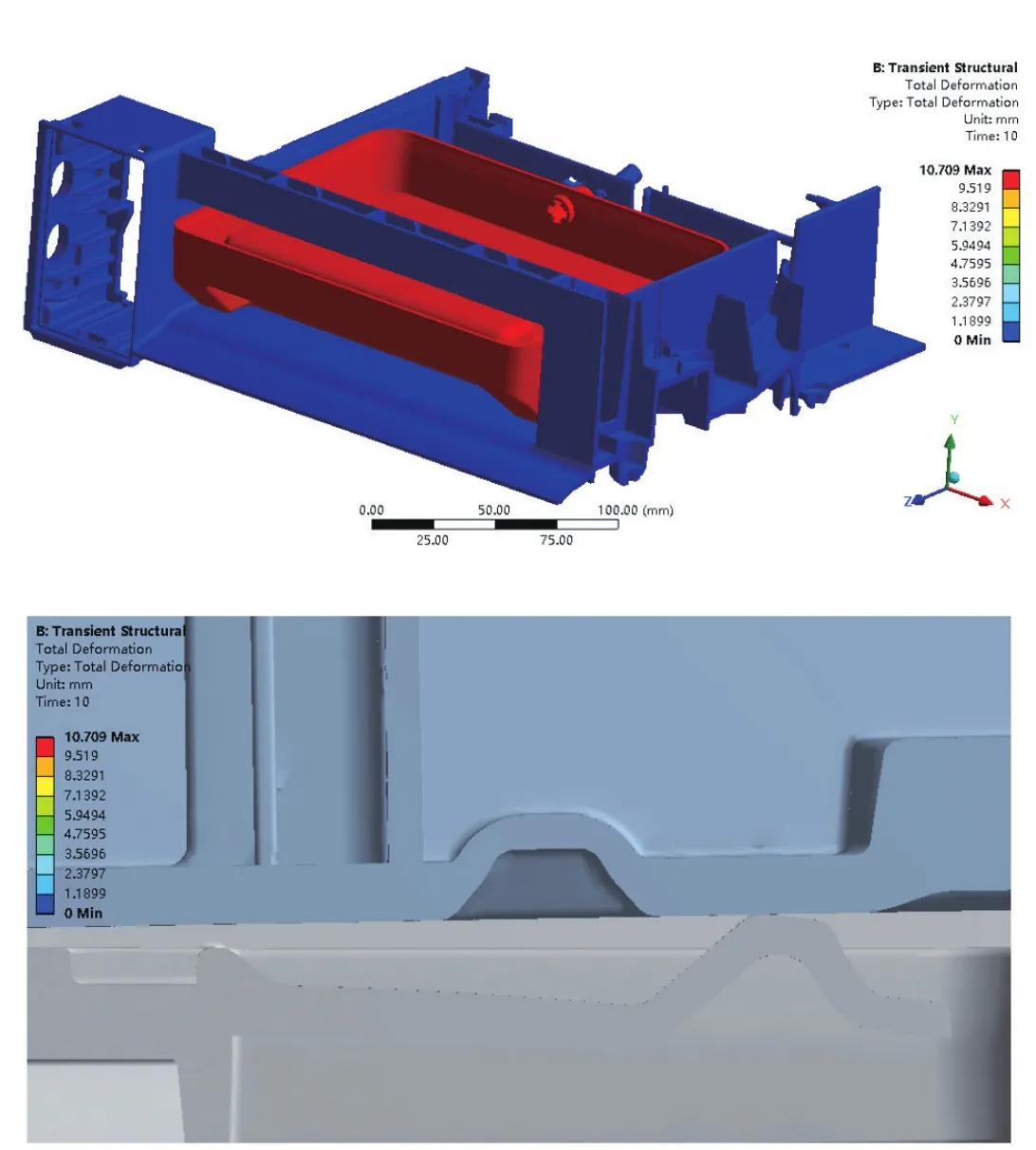
图8 抽屉位移图

图9 卡扣最大变形图

表2列出了拉出过程中拉出力与拉出时间的关系数据，根据表中数据可以得出，拉出过程中的最大拉力是19.164N，发生在1.75s，整理表2中的数据可以得到图12所示的曲线，由图12可以很直观的看出在刚拉出抽屉的时候，拉力波动比较大，在5.71s的时候，拉力趋于平稳接近0，此时卡扣已经被抽屉完全压下，由于本次分析接触为无摩擦（光滑）接触，所以当卡扣被完全压下后，拉出力接近0N。表2中拉出力的正值表示拉出力方向与Z轴正方向一致（图8所示坐标轴方向），负值表示与Z轴反向一致。

5 实验验证

为了验证仿真结果的真实性，根据三维图进行了样机的制作，用于实验测试。实验方法为固定约束样机产品，然后用拉力计拉出抽屉，拉出过程尽量缓慢平稳匀速拉出，时间控制在10s拉出，拉出判断为卡扣和抽屉完全分离，拉力计会自动记录最大的拉力，实验方法如图13所示。图14为拉出过程中拉出力的最大值，根据图14所示，最大拉出力为20.5N。

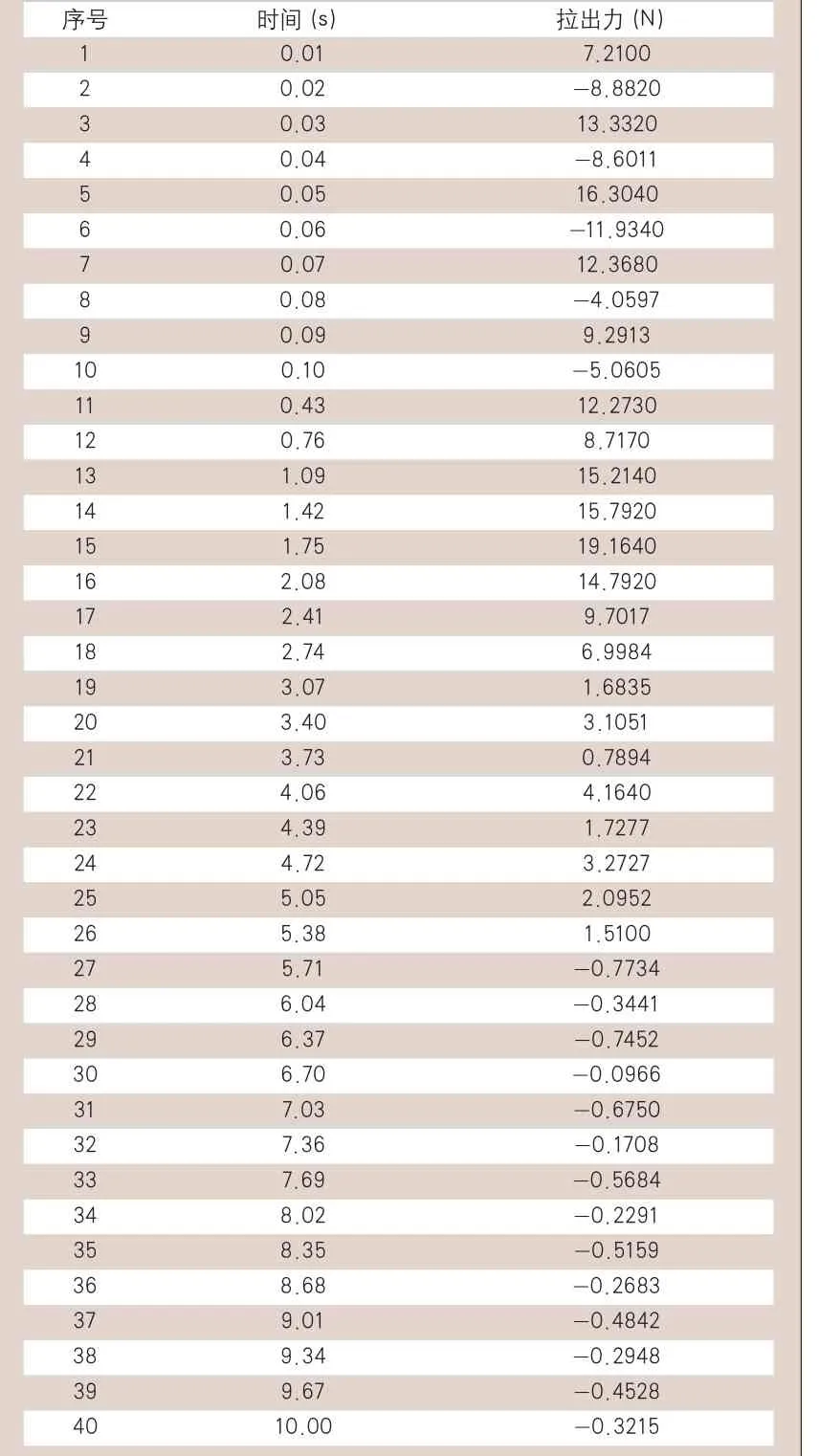
表2 拉出力与时间关系

6 结论

本文对某烹饪器具抽屉结构拉出过程进行仿真分析，在仿真后根据三维模型制作了实物进行拉出力实验。在尽可能保留模型细节的前提下，尽量对每个细节进行高度还原，没有对模型进行通常CAE分析的模型简化处理。目的是测试在不进行模型处理的前提下，仿真所耗用的时间和计算资源有多大，达到的仿真预测效果如何。通过仿真分析预测了卡扣工作时抽屉拉出力为19.164N，而后的实验测量拉力为20.5N，仿真和实验相差1.336N，根据以上数据对比可以得出仿真和实验结果接近，差异为6.5%。

通过以上结论可以得出，应用本文中的仿真分析方法进行抽屉卡扣仿真分析可以得到接近于实验值的预测结果。此种基于Ansys Workbench的分析方案可以应用于卡扣设计中，虽然仿真结果较为接近实验测量值，但是消耗计算资源和计算时间的成本比较高。通过研究文中的应力和变形结果，可以很明显看出在卡扣周围的大部分框架结构的应力和变形几乎为零。也就是说，此部分的结构还可以通过简化方法进行模型简化。对于仿真卡扣结构，工程师可以参考本文中的方案进行评估计算时间成本和前处理时间成本，如果前处理时间（模型简化时间）过长，采用本文所述方案明显要优于模型简化方案。因为本文所述方案消耗人力成本较低，前处理只用了2个小时，大部分工作都由计算机承担，在提交云计算后，节省的人力资源可以直接进行其他项目仿真。此方法为项目繁多的企业或者仿真工程师数量有限的企业提供一种可以借鉴的产品开发仿真分析方案。

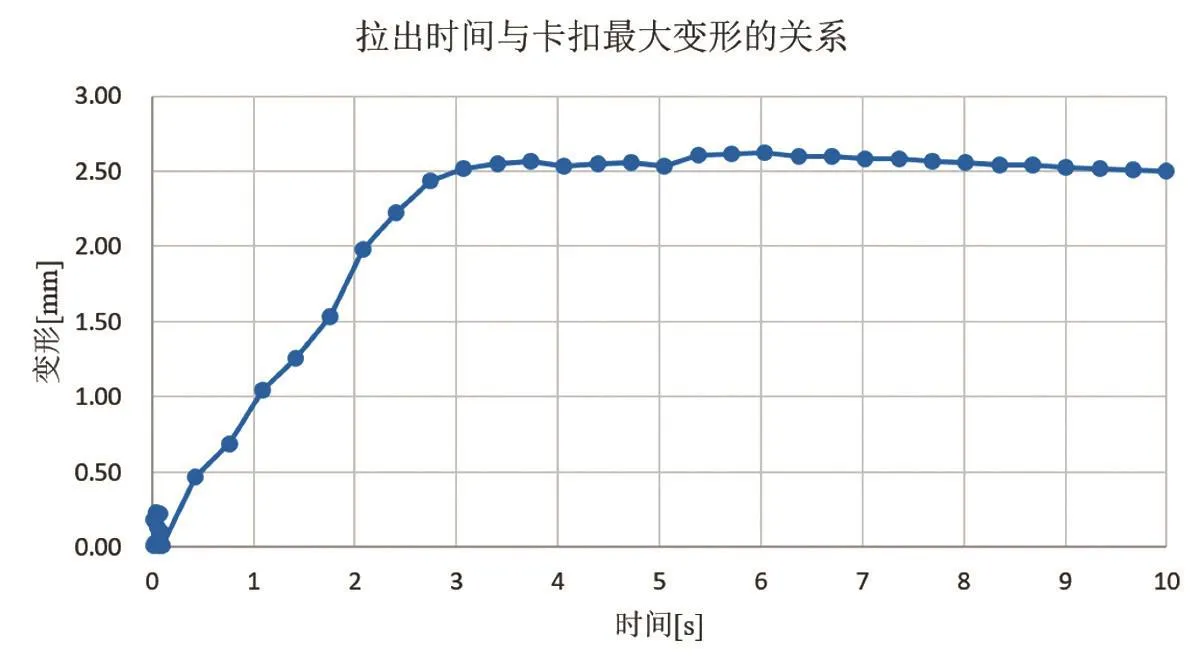
图10 拉出时间与卡扣变形的关系

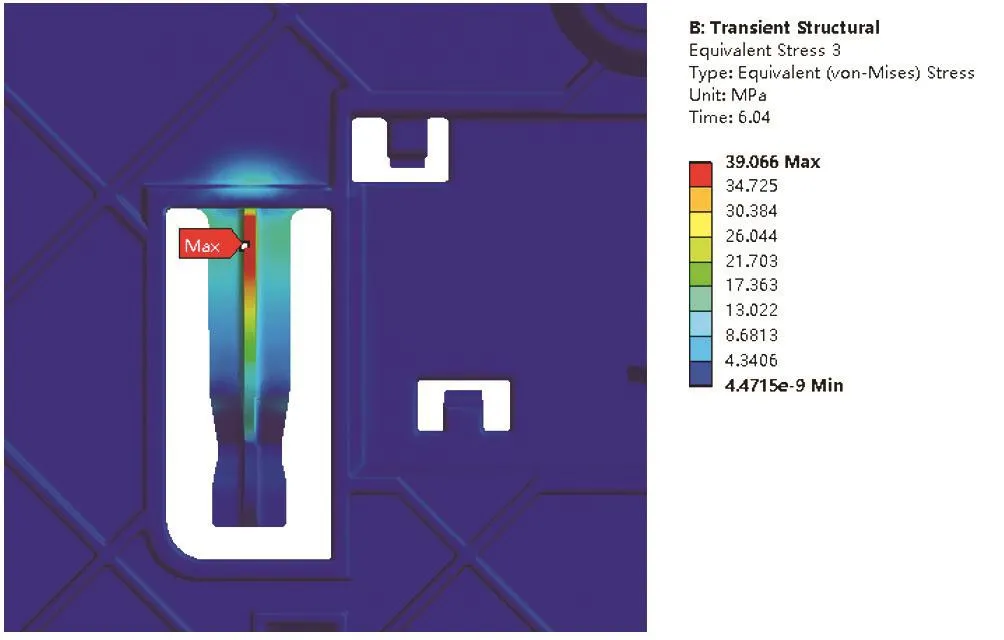
图11 卡扣最大应力图

图12 拉出力随时间变化曲线

图13 实验测得拉出力方法示意图

图14 测得的拉出力值