基于改进飞蛾扑火算法求解多需求点的应急物资调度

贺体龙，楼文高，2

1(上海理工大学光电信息与计算机工程学院，上海200093)

2(上海商学院校长办公室，上海200235)

1 引 言

当今，近年来，灾害性事件频发，给人民群众的生命财产带来了严重的威胁［1］.在突发地震的紧急处理过程中，最重要的工作之一就是供给相应的应急物资，所以开展快速而又有效的物资调度与配送变得至关重要.因此，研究应急物资调度问题具有重要的理论和实践意义.Kemball-Cook［2］在1984年首次提出该问题——对于救援物资的供应和运输需要进行针对性的管理.此后，国内外学者对应急物资调度问题进行了深入探讨，做了大量研究.现有文献［3-11］的研究主要是基于未考虑道路发生损坏情况下的应急物资调度问题，未考虑到道路实际损毁情况.

事实上，地震等灾害发生后，当地道路往往会遭到损坏，物资运载过程中所消耗的时间以及成本也会随道路的损坏程度产生相应的变化.此前很少有学者研究此类问题，王晶等［12］考虑了道路毁坏程度对运行时间的修正，并利用网络流的方法求解;姜春霞等［13］考虑了道路损坏情况、损毁程度及可修复性对车辆运行时间的影响，并引入应急物资调度限制，以最小化配送延迟为目标建立优化模型.陈钢铁［14］等建立道路抢修和应急物资调度模型并采用启发式算法对模型进行求解.Jiang Jincheng［15］等考虑出行时间、道路通行能力和物资供求情况，提出的应急物资车辆调度模型来解决物资调度问题.虽然他们考虑了道路受损的情况，但是事实上，在实施调度之前，通过无人机图像识别技术进行灾害评估和明确道路状态［16-18］，所以本文根据道路通行的状态，选择相应的路线，并建立相应的调度模型.

再则已有研究大多采用粒子群算法［5］、遗传算法［6］、蚁群算法［19］等求解应急物资调度最优化问题.文献［20，21］表明，Mirijalili 等提出的飞蛾扑火优化算法(MFO)其全局搜索能力和局部收敛速度方面明显优于上述最优化算法.但是在高维情况下，MFO 算法会陷入局部最优解，因此本文将使用Trivedi I N［22］等提出的 Levy—MFO 算法(IMFO)进行求解应急物资调度方案.

因此，本文研究运输路网结构存在不同毁坏情况下的应急物资调度问题，以运输过程中物资装载总时间最少、所消耗成本最少为优化目标函数，用IMFO 算法求解最优应急物资调配方案，并与MFO 算法求解的结果进行对比.

2 问题描述与模型建立

2.1 问题描述

设有 m 个灾害需求点 B1，B2，…，Bm，需要 n 个应急物资救援点 A1，A2，…，An，提供 p 种物资 C1，C2，…，Cp，假定 aqi表示第q 种物资在第i 个救援点的储存量，bqi表示第j 个需求点对第 q 种物资的需求量，其中:1≤q≤p，1≤i≤n，1≤j≤m.tqi表示第i 个救援点装载第q 种物资所需要的单位时间.设从第i 物资救援点到第j 个灾害需求可能存在着道路损毁，设道路损毁的路程为Xij，单位距离修复道路的时间为T0，根据路段不同的损毁情况，分配施工队进行施工，0≤α＜β 表示道路可行，无需派遣施工队，表示道路可修复，派遣施工队进行修复，并加以修复时间最晚为Tend进行约束，若修复时间大于Tend，则表示此次路线不通;δ≤α≤1 表示道路不可修复，无需派遣施工队，此次路线不通.要求以运输过程中物资装载总时间最少和所消耗成本最少为优化目标，给出一个最优的调度方案.

2.2 条件假设

假设1.车辆在运输过程中的速度恒定，不考虑出发与到达的速度变化.

假设2.每一种需求(应急)物资的需求(应急)程度相同.

假设3.所有救援点的各种物资数量之和能满足所有需求点所需的各种物资数量之和.

假设4.从Ai到Bj有且仅有一条最短路线.

假设5.每条道路只可能存在一种情况的损坏，即:无损坏、损坏可通行、损坏可修复或者损坏不可通行.

假设6.暂不考虑派遣施工队所消耗的成本.

2.3 模型建立

以运输过程中物资装载总时间最少和所消耗成本最少为优化目标，模型建立如下:因为时间和成本为不同量纲，蒋杰辉［23］提出引入时间成本系数ω，将时间看成成本的一部分，本文再引入权重因子w1、w2，将上述多目标函数转化为单目标函数.从应急物资调度现实需求角度看，时间的权重应大于成本的权重，从而得:

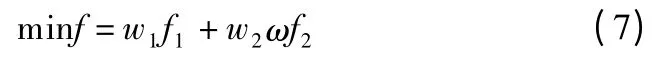
其中:公式(1)和公式(2)分别表示运输成本以及时间成本，cij表示从第i 个救援点到第j 个需求点运输单位物资量所消耗的成本，xqij表示从第i 个救援点到第j 个需求点运输第q种物资量，rij表示从第i 个救援点到第j 个需求点是否可以通行，tqi表示第i 个救援点装载第q 种物资所需要的单位时间;公式(3)表示救援点的第q 种物资量不小于需求点所需求的第q 种物资量，Aqi表示第i 个救援点的第q 种物资量，Bqj表示第j 个需求点需求的第q 种物资量;公式(4)表示从第i 个救援点运输到需求点的第q 种物资量不大于第i 个救援点的所含有第q 种物资量;公式(5)表示从救援点运输到第j 个需求点的第q 种物资量不小于第j 个需求点所需求的第q 种物资量.公式(6)表示第i 个救援点到第j 个需求点的道路是否可行，0 表示道路不可行，1 表示道路可行.

3 算 法

飞蛾扑火优化(MFO)算法是一种新颖的群智能优化算法，该算法的主要灵感来源于飞蛾在自然界中被称为横向定位的飞行方式.MFO 算法的寻优过程可以抽象的理解为飞蛾寻焰与弃焰两种行为.在寻优迭代运算过程中，飞蛾和火焰分别有独特的公式来进行的迭代运算更新自己的位置.其中飞蛾是在搜索空间里的实际搜索主体，而火焰是飞蛾到目前为止搜索到的最好位置.因此，如果飞蛾找到一个更好的解，则每只飞蛾便在标记火焰附近搜索并更新火焰.飞蛾通过这种过程就可以得到它的最优解.通过实验研究发现，MFO 算法在低维情况下有着显著的全局搜索能力，但是随着维度的不断增加，MFO 算法的全局搜索能力会不断的减小，易陷入局部最优.

Trivedi I N 等提出将标准的MFO 算法与Levy 飞行策略相结合，可以提高飞蛾扑火优化算法的求解精度和收敛速率.因此本文将验证改进后的飞蛾扑火优化算法(标准的MFO算法与Levy 飞行策略相结合)—IMFO 算法在高维情况下的全局搜索能力、收敛速率以及求解精度.

为测试IMFO 算法的性能，本文选取 Sphere、Step、Sum-Different、SumSquares、Zakharov、Levy，6 个基准测试函数，使用不同维度(dim=10，30，50，三种维度)对算法测试.设置算法的种群规模40，最大迭代次数为1000.因为存在三种不同的维数和6 种测试函数共18 种情况，所以基于每一种情况，都需独立运行MFO 和IMFO 算法各50 次.不同维度下，两种算法的函数最优值的平均值如表1 所示.从表1 可以看出不同维度下的IMFO 算法的求解精度均高于MFO 算法的求解精度;当维度为50 维时，实验发现MFO 算法易于陷入局部最优，其全部搜索能力小于IMFO 的全局搜索能力.本文选择SumDifferent，Levy、Zakharov 三种测试函数的迭代过程图进行分析如图1、图2、图3 所示(纵轴表示目标函数值，横轴表示迭代次数)，从图1、图2、图3 中可以看出，改进后的 MFO算法在高维空间的全局搜索能力增强显著，易于跳出局部最 优解.

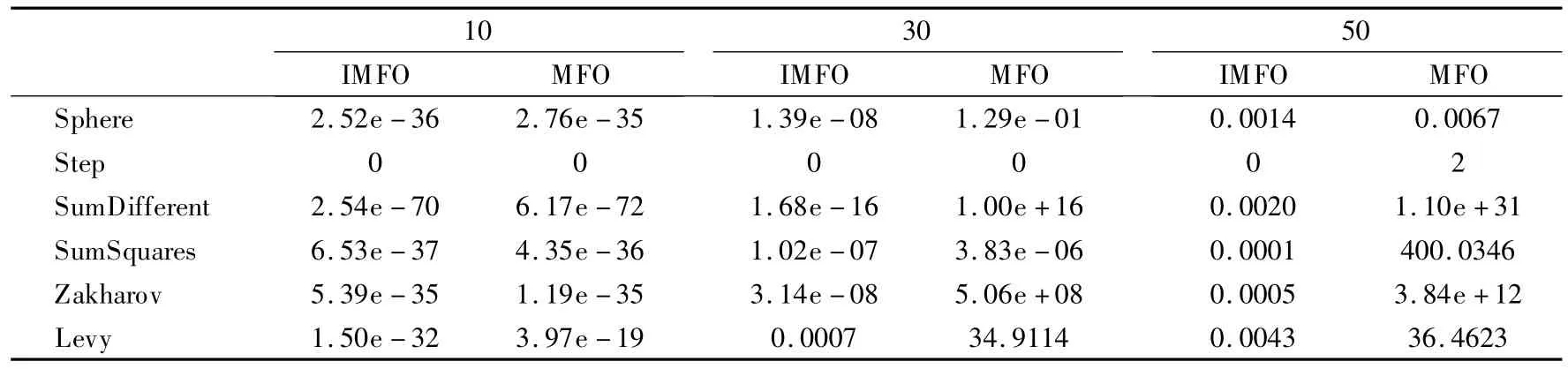
表1 2 种算法不同维度的最优值比较Table 1 Optimal value comparison of two algorithms in different dimension

图1 SumDifferent 函数迭代过程图Fig.1 Performance for SumDifferent

图2 Zakharov 函数迭代过程图Fig.2 Performance for Zakharov

图3 Levy 函数迭代过程图Fig.3 Performance for Levy

4 算例应用

假设在某次地震应急救援中有5 个应急物资救援点A1，A2，…A5和2 个灾害需求点B1和B2，且灾害需求点需求应急物资救援点提供3 种物资，如急救药品(单位:千克)、食品(单位:吨)和帐篷(单位:千顶)分别用 C1，C2，C3表示.其中应急物资救援点可提供的各个物资数量和灾害需求点需求应急物资的数量如表2 所示.

合理假设应急物资救援点到灾害需求点的单位运输量成本c(单位:百元)和应急物资救援点各种物资的单位装载时间(单位:分钟)如表3 所示.

当各个救援点与救援点之间的道路存在损坏时，应急物资救援点到灾害需求点的损坏距离X(单位:千米)以及相应的程度系数 α 如表4 所示(X/α)，且设当 0≤α＜0.2 表示道路可行，无需施工队修复;0.2≤α＜0.75 表示道路可修复;0.75≤α≤1 表示道路不可修复.假设修复时间为0.5 小时/千米，最长可修复时间不得超过3.5 小时，当修复时间超过3.5 小时表示救援点与需求点之间不可通行，反之表示两者之间可以通行.(本文表2 到表4 的数据均为合理性假设得到的随机数据)

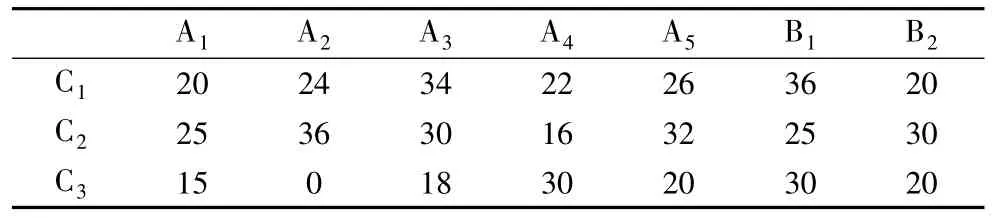
表2 救援点提供物资的数量和灾害点需求物资的数量Table 2 Quantity of supplies provided at the relief point and the quantity of materials needed at the disaster site

表3 单位运输量成本和应急物资装载时间Table 3 Unit transportation cost and the unit loading time of various materials in emergency material supply point

表4 损坏距离和相应程度系数Table 4 Damage distance and corresponding coefficient

通过实验对比运算，IMFO 算法的参数设置如下:飞蛾群体数为500 个，最大迭代次数为2000，个体位置信息的维度是根据算例的5 个救援点分别提供3 种物资到2 个需求点而确定，其维度为30.参考蒋杰辉［23］一文，本文设置时间成本系数ω 为1，权重满足w1+w2=1，本例中根据专家评价法设置权重w1、w2分别为1/4 和3/4，即对于应急物资优化调度来讲，物资装载时间成本比运输成本更重要.

当各个救援点与救援点之间的道路存在损坏时，在相同的迭代次数和相同的种群条件下，使用MFO 算法和IMFO 算法进行15 次的求解运算，得出的最优目标函数适应值的结果如表5 所示.算出两种算法的最优目标函数适应值的最大值、最小值、平均值，其中IMFO 算法的最优目标函数适应值的最大值、最小值、平均值依次为:328.875，323.625，323.975;MFO 算法的最优目标函数适应值的最大值、最小值、平均值依次为 398.475，340.25，357.59.从表5 可知，在 15 次求解中，每次IMFO 算法求解出的目标函数最优值均小于MFO 算法求解的结果，且IMFO 算法求解出的目标函数最优值均在323.625 附近，且求解结果是 323.625 出现了 14 次，占总次数的93.3%.对比 IMFO 算法和 MFO 算法的最大值、最小值、平均值，明显IMFO 算法求解结果优于MFO 算法求解结果.

当各个救援点与救援点之间的道路不存在损坏时，通过IMFO 求解出的目标函数的最小值为305.625，其相应的应急物资调度方案如表6 所示.

表5 两种算法下的最优目标函数适应值Table 5 Optimal fitness of objective function under two algorithms

选择15 次实验中的一次实验数据，通过IMFO 求解得到目标函数的最小值为323.625，目标函数适应值的变化过程如图4 所示，其相应的应急物资调度方案如表6 所示.对比两种情况下的目标函数适应值以及调度方案表明:在道路损坏情况下，物资装载过程中所消耗的时间以及运载成本明显增加，对于本例条件下，增加约5.9%.

图4 目标适应值的迭代图像Fig.4 Iterative image of target fitness

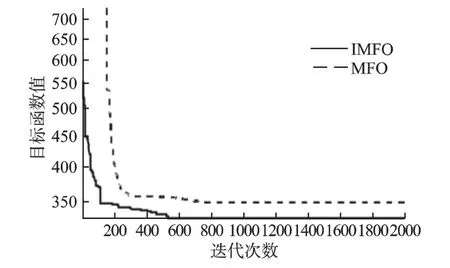
图5 MFO、IMFO 最优化迭代过程示意图Fig.5 Schematic diagram of optimization iteration process of MFO and IMFO

采用MFO 算法求解道路损坏情况下的应急物资调度方案如表6 所示，最优化迭代曲线如图5 所示，虚线为MFO 算法的目标函数值迭代曲线，实线为IMFO算法的目标函数值迭代曲线.MFO 算法的最小目标函数值为 352.625，大于IMFO 算法求解得到的最优目标函数适应值.从图5 可知，IMFO 算法的迭代速率快于MFO 的迭代速率，也较MFO 算法在迭代中最先达到最优解，由此可见，IMFO 算法在高维情况下的全局搜索能力方面比MFO 更强，不易陷入局部最 优解.

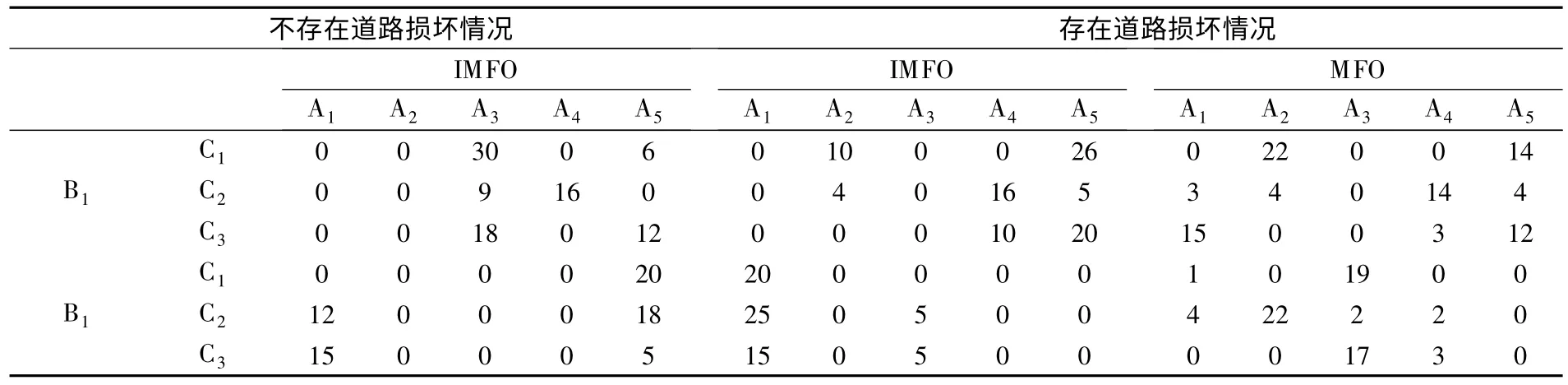
表6 IMFO 和MFO 算法求解应急物资调度方案Table 6 IMFO and MFO algorithms for emergency material scheduling

5 结束语

本文研究基于道路损坏情况下的道路可行、道路可修复和道路不可通行三种条件下的多救援点对多需求点的多种应急物资调度问题，通过数据的预处理判辨救援点到需求点是否存在物资运输，建立同时兼顾运输过程中物资装载总时间最少和所消耗成本最低的优化目标函数，使用改进的飞蛾扑火优化算法——IMFO 求解最优应急物资调配方案.通过测试函数测试和算例以及仿真实验验证了IMFO 算法在应急物资调度的有效性以及可用性，并通过改进后飞蛾扑火优化算法求解出了一个基于道路损坏情况下的紧急物资调度方案，具有一定的实用性的、较好的社会应用价值，与MFO 的结果进行对比说明，IMFO 具有更优的全局搜索能力和局部收敛速度.本文的不足之处是通过具体的算例而不是采用真实数据进行实验分析，以及道路可行、道路可修复和道路不可通行三种条件都是静态情况下的，在实际运输过程中，道路情况往往是会有变化的.基于道路损坏对应急物资调度的影响是未来研究的主要方向，应用性能更优(收敛速度更快、全局搜索能力更强)的群智能最优化算法进行结果求解可以解决更复杂的真实物资调度最优化问题.