结合新概念分解和频繁词集的短文本聚类

贾瑞玉，陈胜发

(安徽大学计算机科学与技术学院，合肥230601)

1 引 言

文本聚类作为高效组织、导航、检索和总结大型文本集合的重要工具，受到了广泛的关注.因此，对短文本进行聚类有很大的应用价值，例如:可以挖掘用户评论中的观点［1］，检测社交媒体中的话题［2］和情感分析［3］等.由于短文本表达灵活多样，文字简短且增长迅速，所以特征稀疏、特征难提取和噪音数据多等特点，传统的适合长文本以及小数据量的聚类算法是难于处理，因此有效的短文本聚类算法需要被研究出来.近年来，基于矩阵因子的文本聚类方法已经得到了广泛的应用.特别是非负矩阵因子分解(Nonnegative Matrix Factorization，NMF)［4］和概念因子分解(Concept Factorization，CF)［5］.

一般来说，NMF 的目标是找到两个非负矩阵因子，它们的乘积与原始数据矩阵近似.NMF 中的非负约束产生了基于部件的文本文档表示，因为它们只允许加法组合，而不允许减法组合［6］.NMF 的主要限制是它只能在数据点的原始特征空间中执行.为了解决这一局限性，Xu 和 Gong 提出了CF 方法［7］，CF 保留了NMF 的所有优点，也可以在任何数据表示空间［8］中执行.在文档聚类中使用CF 方法时，每个文档都由聚类中心的线性组合表示，每个聚类中心由数据点的线性组合表示.由于线性系数具有明确的语义意义，因此可以很容易地从这些系数中得到每个文档的标签.

最近的研究表明，在机器学习中使用额外的监控信息可以提高学习性能［9，10］.为此，通过使用监控信息来指导学习过程的方法提出了许多关于CF 的扩展.监控信息要么合并到基本CF 模型中，要么合并到图结构中.在这些CF 的扩展中，约束概念分解(Constrained Concept Factorization，CCF)［11］使用确切的标签信息作为额外的硬约束.这个模型确保在新的表示空间中将具有相同类标签的数据点严格地映射表示.CCF 的局限性在于它忽略了数据集的局部几何结构信息.为了解决这个问题，局部正则化约束概念分解(Local Regularization Cons-trained Concept Factorization，LRCCF)［12］将局部几何结构信息和标签信息合并到CF 模型中.约束邻域保留概念分解(Constrained Neighborhood Pre-serving Concept Factorization，CNPCF)［13］使用含有必要连接约束形式的监控信息来修改图.然而，当监控信息是有限的时候，这些信息无法有效的保持数据集的几何结构.因此，有必要提出一种新的CF 框架，它可以利用无约束数据点并且同时保持数据集的局部几何结构.

对于传统文本表示的语义缺失和高维问题，基于频繁词集的文本聚类可以很好的解决.在文本集中有很多文本都出现某些词，这些词的集合被称为频繁词集，并且这些词的集合可以对一些关于主题的语义起到很好的表示作用.文献［14］对文本表示是使用挖掘出的频繁词集，并且对于文本之间的相似度也是使用共有的频繁词集的数量来表示的，然后进行文本聚类.文献［15］提出了一种基于频繁词集的文本聚类方法(frequent itemsets based document clustering method，FIC).该方法首先对预处理过的文本集进行频繁词集的挖掘，然后采用挖掘出来的频繁词集来构建文本表示模型，接着将每个文本看作节点，文本间的相似性看作节点之间的边，来构建成文本网络，最后使用社区划分的算法进行文本聚类.

为了解决传统文本表示的高维和语义缺失，本文利用文献［15］的优点，提出了一种结合新概念分解和频繁词集的短文本聚类(Combining new con-cept factorization with frequent itemsets for short text clustering，CFFIC).该方法首先挖掘出频繁词集，运用频繁词集来构建文本表示模型.然后利用无约束数据点，提出了正则化概念分解(Regularized concept factorization，RCF)进行聚类.该算法不仅能对处理后的文文本的维度起到很好的降低作用，还可以很好的关联短文本集中文本，并且提出的新正则化概念分解算法(Regularized concept factorization，RCF)很好解决了CF 算法在监控信息不足的情况下的缺陷，使得聚类效果得到了有效提升.

2 CFFIC 算法

CFFIC 算法流程图如图1 所示.该算法使用频繁词集构建的文本表示模型可以很好解决数据稀疏和维度的问题.

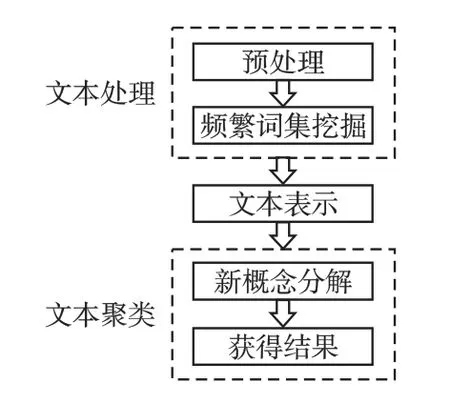
图1 CFFIC 算法框架Fig.1 CFFIC algorithm framework

图1 表示本文算法的主要过程，分别为预处理、频繁词集挖掘、文本表示、新概念分解、获得结果.首先预处理就是对文本集进行分词和去停用词;然后挖掘出频繁词集，使用这些频繁词集构建文本表示模型;最后使用RCF 算法进行文本聚类以获得结果.算法中的关键步骤的具体介绍如下.

2.1 频繁词集挖掘

本文采用文献［16］中的算法进行频繁词集的挖掘.该算法的最小支持度是通过文本的数量来获得，然后挖掘出频繁词集(特征选择之后).相关定义如下:

定义1.(文本数据库)就是进行过分词和去停用词的文本组成的，定义为 A={A1，A2，…，An}.

定义2.(频繁词集)通过最小支持度，得到频繁词集集合，定义为 O={O1，O2，…，Om}，其中 Oi表示一个频繁词集，Oi={w1，w2，…，wt}，其中 wi表示一个词.

2.2 文本表示模型

本文算法是使用频繁词集构建文本表示模型.也就是构建文本-频繁词矩阵M，矩阵M 为0-1 矩阵，定义如下:

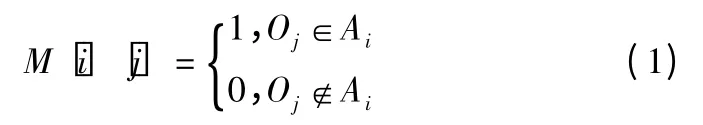
其中，M［i］［j］表示矩阵 M 中文本 Ai是否存在频繁词集 Oj，若文本 Ai中有频繁词集 Oj，则 M［i］［j］=1，否则M［i］［j］=0.使用频繁词集来代替文本中的特征单词的方法可以很好的解决维度和文本稀疏的问题.频繁词集本身是可以反映出文本的主题，例如:{window}表示装饰类，{apple}表示水果类，若{apple，window}同时出现可以表示出计算机类，而{apple，window}就是一种频繁词集.因此，文本间相似度用频繁词集来计算，可以很好的避免不同文本产生过大的相似度而影响聚类效果.

2.3 RCF 算法

正如我们前面提到的，在有空监控信息的情况下，传统的CF 算法的很难利用任何监控信息.下面详细介绍一种充分利用监控信息的新型正则化CF 方法.

关于监控信息，明确的标签信息可能难以收集.在实践中，我们发现了另一种相对容易获取监控信息的方式.我们称之为对偶连通约束信息.具体地说，一对具有相同标签的数据点表示为必要连接约束，否则表示为不能连接约束.然而，相反的过程可能是不正确的.换句话说，一般情况下仅从对偶连通约束中直接导出数据点的显式标签是很难的.这表明，对偶连通约束提供了一种监控信息，这种信息本质上是较弱的，因此比数据点的实际标签更通用.所以在下面的RCF 方法中，双连通约束作为先验信息.

一般情况下，约束信息的获取是非常困难的，因为在这个过程中需要投入大量的人力和物质.但CF 方法在有限的约束信息的情况下，其性能是无法得到很大的提高.为了克服这一局限性，我们将这些约束映射到无约束数据点上，来获得整个数据集的约束信息.然后将获取的约束信息添加到CF 目标函数中，构建RCF 模型.

2.3.1 约束传播

传播过程可以看作是一个两类分类问题［17］.一对约束数据点之间的关系可以编码为+1 或－1.传播过程决定了两个无约束数据点之间的约束关系.这个过程完全等价于对标记为+1 的类或标记为－1 的类之间的关系进行分类.

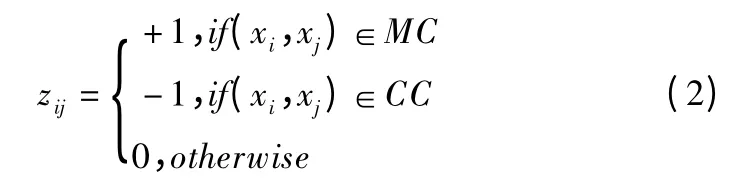
Step 1.通过定义 k-NN 图的权重矩阵 W={wij}N×N，构造一个k-NN 图，wij的定义如下:

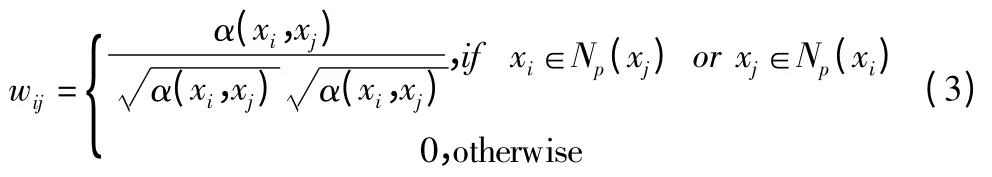
Step 2.计算归一化图的拉普拉斯矩阵 L=I－D－1/2WD－1/2，其中是一个对角矩阵，dii=∑jWij.

Step 5.F*=是传播的对偶连接约束的最终表示，其中是 {Fh( t )}的极限.

Step 6.通过利用F*和原始权重矩阵W 构造一个新的权重矩阵

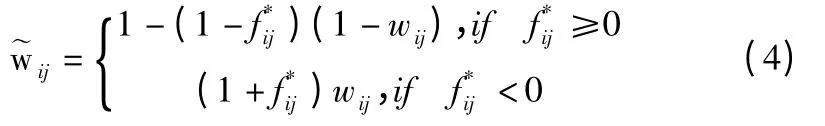
通过上述方法，可以收集更多关于数据集的约束信息.利用对偶连接约束信息重构权值矩阵.也就是说，如果一对数据点属于同一个类，那么连接它们的边的相应权值就会被赋一个大得多的值，否则权值就会被赋一个小得多的值.

2.3.2 RCF 的目标函数

在本小节中，我们通过将权重矩阵嵌入CF 目标函数，详细介绍了 RCF 的构造.以下术语用于保存数据集的监控信息:

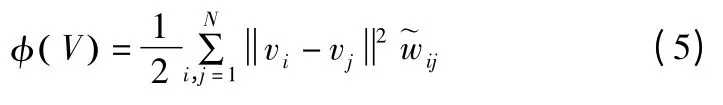
当xi和xj具有相同的类号时，xi应该和xj一起出现在原始几何空间中，并且会被赋一个较大的正值.根据的定义的值也会很大.最小化 φ( V )，vi和 vj应该有一个较小的欧式距离，这样在低维表示空间中vi和vj也应该彼此靠近的.相反，当xi和xj具有不同的类号时，xi和xj应该在几何空间中彼此远离，并且会被赋一个较大的负值，从而的值会较小.因此，当vi和vj属于一个类时，vi和vj的结果会有很大的不同.根据上面的分析，我们发现在低维表示空间中φ( V )可以产生一起出现的具有相同标签的点和彼此之间距离非常远且属于不同类的点.这与原始空间中点的内在几何关系是一致的.通过最小化(5)，利用有限的对偶连通约束信息可以有效地保持数据集的原始几何形状.如果选择欧氏距离来度量近似的质量，则RCF 的目标函数为:

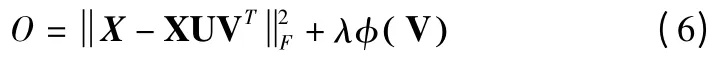
在公式(6)中，第一部分可以看作是重构项，这一项可以保证近似的效果.第二部分可以看作是一个约束项，这一项的目的是保持数据空间原有的几何结构.在RCF 目标函数中，正则化参数λ≥0 控制这两个部分的比例.

2.3.3 更新 RCF 规则

公式(6)中的目标函数可以重写为:

其中tr(·)为矩阵的轨迹，D～ 表示对角矩阵，其项是 ～W 的列和.

对于uij＞0 和vij＞0，我们分别分配两个拉格朗日乘数ψ=［ψij］和 φ=［φij］.ψij和 φij是包含拉格朗日乘数的矩阵.然后，目标函数可以重写为:

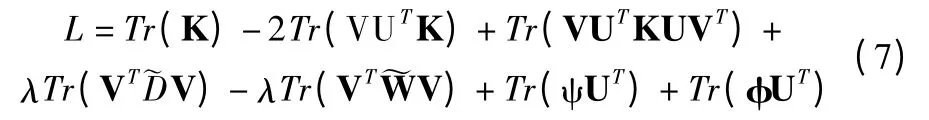
公式(14)中，关于U 和V 的偏导为:

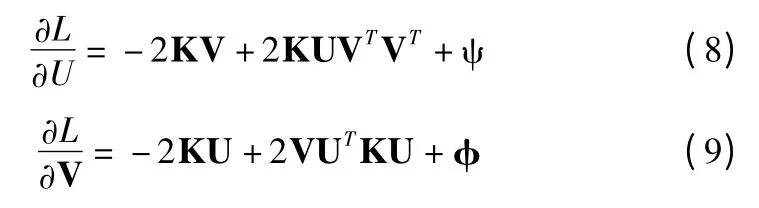
使用 Karush-Kuhn-Tucker(KKT)(条件为 ψijuij=0 和φijvij=0)，我们会有以下关于uij和vij的方程.

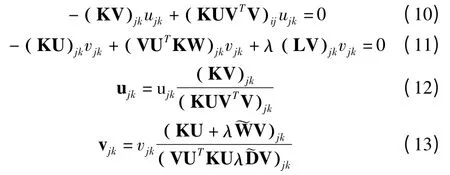
上述最小化目标函数O 的方法并不是唯一的.如果U 和V 是 O 的解，UQ 和 VQ－1也会形成任意正对角矩阵 Q 的解，这是很容检验的.因此，我们进一步规范化解决方案，使其惟一.设uc为U 的列向量，在和 UVT不变的条件下，对U 和V 进行归一化更新:

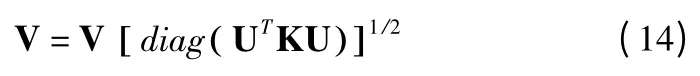
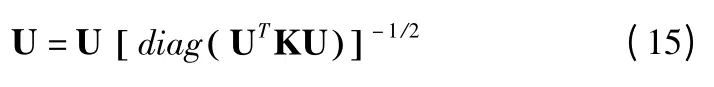
3 实验及结果分析

为了说明本文算法如何提高短文本聚类的性能，我们将CFFIC 算法与3 种具有代表性的短文本聚类算法进行比较，分别是 FIC、CNPCF 和 RNMF.RNMF 则采用 l2，1范数设计目标函数.并且这3 种算法与CFFIC 算法都使用TF 作特征度量.

3.1 评价标准

通过将每个文档的聚类标签与数据集提供的原始标签进行比较，评价聚类结果.采用准确度(AC)和归一化互信息度量(NMI)两种标准度量来度量聚类性能.该准确度用于计算正确预测标签的百分比，定义为:

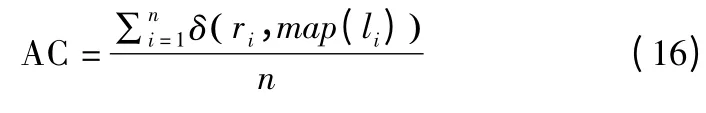
采用归一化互信息矩阵来表示两个簇的相似性.给定两个簇C 和C'，对应的互信息矩阵计算为:

其中p(ci)和p(cj')分别表示随机选取的数据点属于类簇C和C'的概率，p(ci，cj')表示所选点同时属于两个簇的概率.

在实验中，使用标准化度量 NMI(C，C')∈(0，1)，定义如下:

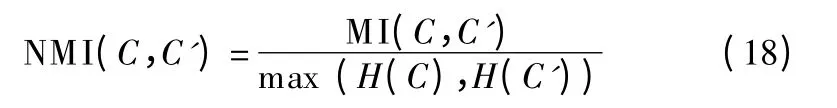
其中H(C)和H(C')表示C 和C'的熵.当选取的两个样本相同时，NMI 取 1，当两个样本完全独立时，NMI 取 0.NMI 值越大，表明聚类性能越好.

3.2 实验数据

本文算法的实验是使用搜狐新闻数据集和新浪微博数据集.实验随机选取了搜狐新闻数据集中10 个类别的数据作为Sohu 短文本数据集，各类别名称及短文本数量如表1 所示.实验对新浪微博数据集是按预先设置的10 个区分度最高的主题词分别抽取相关数据作为Weibo 短文本数据集.各类别名称及短文本数量如表2 所示.

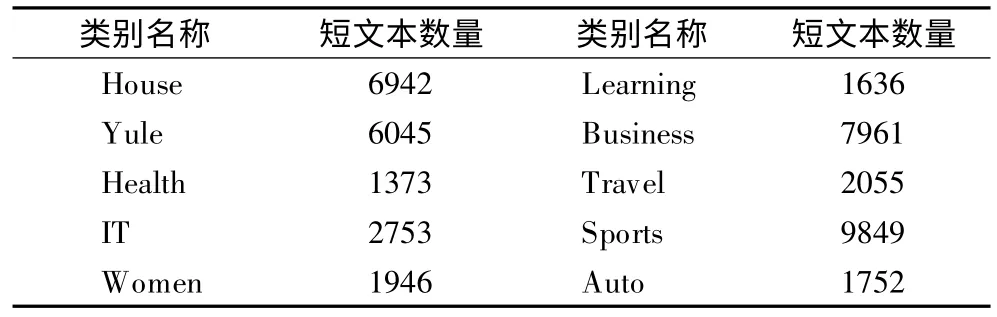
表1 Sohu 短文本数据集Table 1 Dataset of Sohu essay

3.3 相关算法的参数设置

由于 CFFIC 算法、FIC 算法、CNPCF 算法和 RNMF 算法都要指定k 值大小，所以将这四种算法的 k 值大小设置为Sohu 短文本数据集和 Weibo 短文本数据集的类别数目.CNPCF 和CFFIC 都需要使用监控信息，并且为了说明在监控信息非常有限的情况下，本文算法的有效性，监控信息量设置为t=2%.而且通过多次实验得到能保证每个文本以至少5个频繁词集来表示的最小支持度最好.

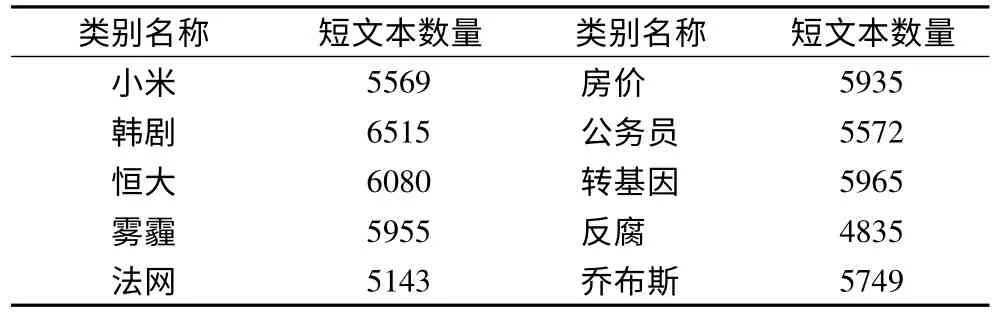
表2 Weibo 短文本数据集Table 2 Dataset of short articles on Weibo

3.4 聚类性能比较

由于 Sohu 和Weibo 数据集中的每一条短文本都具有分类标签，因此聚类质量(NMI 和AC)和运行时间是评价各个短文本聚类算法的非常好的标准.对比实验中，每个算法都以数据集的前1 万条数据，并以1 万的数量进行增加的方式进行多次短文本聚类实验.表3 和表4 分别为各种算法在两个数据集不同短文本数量情况下的 AC 和 NMI 的实验结果，图2 和图3 则为相应的运行时间对比情况.

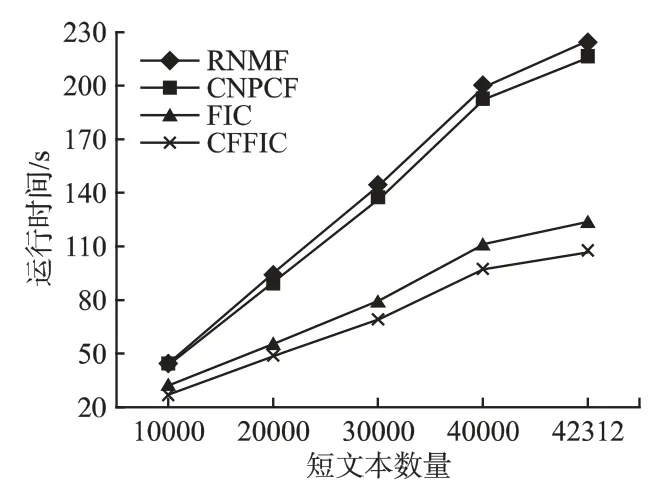
图2 Sohu 的运行时间Fig.2 Running time of Sohu

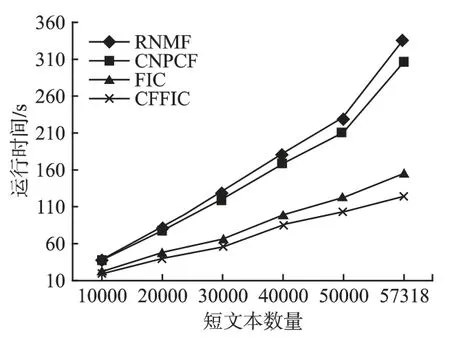
图3 Weibo 的运行时间Fig.3 Running time of Weibo

3.4.1 聚类质量

首先就是聚类质量对比，从表3 和表4 可以看出，在两个数据集的各个不同短文本数量下CNPCF 和CFFIC 的AC 和NMI 均优于RNMF，这是因为CF 继承了NMF 的所有优点，作为扩展的CF 也是优于NMF 的扩展.此外，可以发现虽然在 Sohu 数据集上 CNPCF、CFFIC 以及 FIC 的 AC 和 NMI 的数值较为接近，但在Weibo 数据集上CFFIC、FIC 要明显优于CNPCF，其中FIC 的 AC 和 NMI 的平均值分别比 CNPCF 提高了 39.2% 和 23.7% ，而 CFFIC 的 AC 和 NMI 的平均值分别比CNPCF 提高了40.5% 和24.7%.原因在于书写微博内容比较随意但书写新闻标题是需要严谨规范的，因此Weibo数据集的噪音数据的数量比 Sohu 数据集多，而采用频繁词集进行特征选择的具有更好的鲁棒性，可以降低噪声数据对于聚类质量的影响.

表3 Sohu 数据集的AC 和NMITable 3 AC and NMI of Sohu dataset

表4 Weibo 数据集的AC 和NMITable 4 AC and NMI of Weibo dataset

3.4.2 运行时间

其次在运行时间对比方面，从图2 和图3 可以看出，在两个数据集上 CFFIC 均要明显优于CNPCF、FIC 和RNMF，并且随着短文本数量变得越大的时候，运行时间的差距就越大.例如，在 Weibo 数据集中，当短文本数量达到最大时，CFFIC仅需要123s，而 CNPCF、FIC 和 RNMF 分别需要 305s、154s和 337s.CFFIC 比 CNPCF 和 RNMF 的运行时间少很多，是因为CFFIC 采用频繁词集代替词来构建文本表示模型，这样就大大的降低了数据的维数，计算复杂度也大大的降低了.但是同样都是使用频繁词集来构建文本表示模型的，CFFIC 比FIC 的运行时间快，这是因为FIC 需要计算每个文本对象之间的相似度，而CFFIC 则不需要这样计算，所以CFFIC 在运行时间上快于FIC.

4 结 论

本文提出了一种新的正则化概念分解方法，通过传播有限约束信息来获取更多的约束信息，并利用这些约束信息来保持数据空间的几何结构，提高了聚类的性能.使用频繁词集来构建文本表示模型，解决了数据稀疏和高维的问题.由于考虑了多个文本间的关系，聚类性能再一次得到了一定程度的提升.通过2 个短文本数据集的实验，表明了 CFFIC 具有较好的聚类质量和较小的时间开销.至今文本聚类一直是一个值得深入研究的课题，其面临着数据集规模海量增长的问题.因此，在下一步工作中，将重点研究基于Spark 的CFFIC 的实现方法，目的在于让其可以处理更大规模的短文本聚类问题.