三维Lieblattice模型的能谱结构

刘书言, 于 静

(辽宁石油化工大学 理学院, 辽宁 抚顺 113001)

在凝聚态物理中,材料的宏观性质与能带结构有着密不可分的联系。根据能带的填充情况,可以将材料划分为金属、半导体和绝缘体[1]。随着对拓扑物态研究的不断深入,传统意义上的能带理论也被极大地拓展,材料的类别被更详细地划分。对拓扑物态的研究已成为凝聚态物理学的重点研究方向之一[2]。Lieb lattice模型不仅具有独特的简立方对称结构,在该模型上可以研究量子霍尔效应[3]和量子反常霍尔效应[4],探究拓扑量子相变所需要的条件还具有其他有趣的性质,如非线性衍射、超导跃迁、自旋涨落与超导配对对称性[5],磁霍尔效应,磁相图,分数阶chern绝缘子[6]等。近年来,已有多个研究团队对二维(2D)Lieb lattice模型进行深入研究并取得突破性的进展[7-10],但对三维(3D)的研究还处于初级阶段。本文研究了3D模型的能谱特征,并在模型上施加自旋轨道耦合作用,分析了对其能谱产生的影响。

1 3D Lieb lattice模型

2D Lieb lattice模型是一种具有各向同性最近邻跃迁的正方边心格子[11]。由于其特殊的拓扑结构和物理性质在近些年得到了研究者们广泛的关注与研究。2D Lieb lattice模型上的每个原胞中都含有3个不同的原子,其几何结构如图1(a)所示,3个原子分别标记为A,B,C,2个最近邻格点间的晶格常数为a[12]。在Lieb lattice模型上可以实现对拓扑物质状态的研究。其能谱是由在单个Dirac点上接触的2个色散带和1个零能平带组成的具有对称性的三能带结构,这也是Lieb lattice模型最为显著的特点。对于2D Lieb lattice模型,在没有自旋轨道耦合作用时,其能谱中的2个色散带始终有1个接触点位于零能平带上,也就是说其能带间隙始终是闭合状态。而若想打开其能带间隙则必须要施加1个非零的自旋轨道耦合作用[13]。这不禁引起了本文思考,这一特性在3D Lieb lattice模型中是否也同样适用。

本文在2D Lieb lattice模型中施加层间耦合作用,可以得到如图1(b)所示的立方结构,该立方结构仍然是由A,B,C 3种原子构成,模型的晶格常数为a。

(a)—2D Lieb lattice模型; (b)—3D Lieb lattice模型图1 Lieb lattice模型Fig.1 Lieb lattice model

在紧束缚近似下,该模型的哈密顿量由以下几部分组成,可以表示为

H=H0+H1+H2+HI

其中:H0为化学势项;H1为最近邻格点之间的跃迁项;H2为次次近邻格点之间的跃迁项:

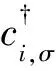
模型的哈密顿量在动量空间可以表示为

基矢为Ψk=(cA,k,↑,cB,k,↑,cC,k,↑,cA,k,↓,cB,k,↓,cC,k,↓)T,在此基础上,其哈密顿量可以展开成为矩阵的形式:

为方便计算,均取晶格常数a为单位长度1,其中h±(k)可以表示为

其中:Cu=cos(ku);u=x,y,z;Cu/2=cos(ku/2);Su/2=sin(ku/2)。

对此哈密顿矩阵进行对角化,可以得到该立方格子模型的体能带表达式为

其中Cx±y=cos(kx±ky)。若不考虑次次近邻跃迁,3D Lieb lattice模型将退化成2D Lieb lattice模型,取λ=0,t′=0,ky=kz=π,取t为单位能量,可以看到图2(a)所示的处于简并状态的能带图,由图像可以观察到中间的能带为平带,上下2条色散带与该平带相形成狄拉克锥结构,3条能带有且仅有1个简并点在(π,π,π)。

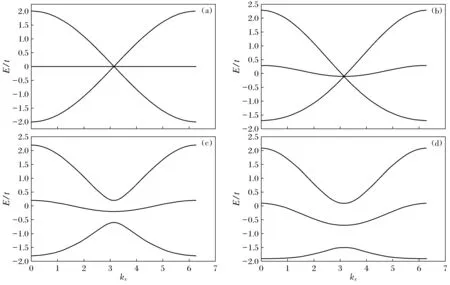
(a)—t=1; μ=0.5;λ=0; t′=0; ky=kz=π; (b)—t=1; μ=0.5; λ=0; t′=0.1; ky=kz=π;(c)—t=1; μ=0.5; λ=0.1; t′=0.1; ky=kz=π; (d)—t=1; μ=0.5; λ=0.2; t′=0.1; ky=kz=π图2 3D Lieb lattice模型能谱Fig.2 Energy spectrum of 3D Lieb lattice model

若在此基础上加入层间次次近邻跃迁的影响,看到如图2(b)的能带图,通过和图2(a)的对比不难看出其能谱图像仍为狄拉克锥结构,3条能带在(π,π,π)点有且仅有一个简并点。不同的是,加入次次近邻作用后其中间的能带在零能附近,为近似平带。当施加自旋轨道耦合作用在次近邻跃迁上,即λ≠0时可以得到如图2(c) 所示的能谱图像,可以看到当λ≠0时,能带间打开了一个完整的间隙,并且随着自旋轨道耦合强度的增加,能隙将越来越大(图2(d))。

2 3D广义Lieb lattice模型

图3 3D广义Lieb lattice模型,由A(方形), B(圆形),C(三角形)3个原子组成Fig.3 3D generalized Lieb lattice model, consisting of three atoms: A(square), B(circle) and C(triangle)

上一节本文将2D Lieb lattice模型加入层间耦合从而得到1个新的3D Lieb lattice模型,讨论了其能谱随自旋轨道耦合强度的改变从而发生的变化,得到的结果与2D Lieb lattice模型类似,即要想打开能带间隙消除简并点的必要条件是施加非零的自旋轨道耦合作用,那么对于这一结论是否适用于3D广义Lieb lattice模型呢?3D广义Lieb lattice模型同样是由A,B,C 3种原子组成,值得注意的是,3种类型的原子不仅存在于立方体的边和面心上,在立方体的中心还存在1个A原子(图3)。

在紧束缚近似下,该模型的哈密顿量可以表示为

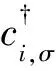
该哈密顿量的基矢为

Ψk=(cA,k,↑,cB,k,↑,cC,k,↑,cA,k,↓,cB,k,↓,cC,k,↓)T,

在此基础上,哈密顿矩阵可表示为

h±(k)可以表示为

其中:Cu=cos(ku);Cu/2=cos(ku/2),u=x,y,z。

选取参数t1= 1,t2= 0.8,t3= 0.5,t4=0.1,t5= 0.2,ky=kz=π,并对角化该矩阵得到图4(a),由图像可知,在未施加自旋轨道耦合作用时,广义三维Lieb lattice模型的能谱图像仍是由3条能带构成且在低能下呈狄拉克锥结构,上下2条色散带与中间带有1个简并点, 中间带在零带附近为近似平带。

若只在该模型其中1个平面(如XY平面)的次近邻跃迁上施加自旋轨道耦合作用时,

其中:Sx/2=sinx/2;Sy/2=siny/2;λ为自旋轨道耦合强度。

选取参数kz=π,t3=t4=t5时对矩阵进行对角化可以得到三维广义Lieb lattice模型的能带表达式为

其中:Cu=cosku,Cx±y=cos(kx±ky)。

取各个跃迁项跃迁强度参数为t1=1,t2=0.8,t3=0.5,t4=0.1,t5=0.2,λ=0.2,且kz=ky=π时,可以得到图4(b)所示的能谱图。

(a)—无自旋轨道耦合作用; (b)—在XY平面施加自旋轨道耦合作用图4 3D广义Lieb lattice模型能谱图Fig.4 Energy spectrum of 3D generalized Lieb lattice model

在XZ与YZ平面的次近邻跃迁上施加自旋轨道耦合作用得到的带隙结构与在XY平面施加自旋轨道耦合作用相似。因此,若要在能带中间打开1个完整的带隙,可以通过在模型空间中的任意1个平面施加自旋轨道耦合作用来实现。

3 结 论

本文在自旋轨道耦合作用存在的情况下研究和讨论了2种3D Lieb lattice模型的能谱结构。研究结果表明,在3D Lieb lattice模型中,加入次次近邻跃迁会影响其能谱图像中的零带,使其产生带宽成为近似零平带。若在模型中加入自旋轨道耦合作用,当自旋轨道耦合强度为零时,其能谱由3条能带组成,且3条能带有且仅有1个简并点,只有在自旋轨道耦合强度不为零时,才能打开其能带间隙,并随着自旋轨道耦合强度的增加,能带间隙会逐渐变大。

Lieb lattice模型为研究拓扑物质的特性和拓扑量子相变提供了可能,在该模型上施加自旋轨道耦合作用时其能带间隙被打开,这一研究有助于实现物质由其拓扑半金属性到拓扑绝缘体性的转变。