基于小波变换与卷积神经网络的图像去噪算法
陈清江,石小涵,柴昱洲
(1.西安建筑科技大学 理学院,陕西 西安 710055;2.空间电子信息技术研究院,陕西 西安 710000)
引言
在图像传感过程中,噪声污染是不可避免的,它严重地降低了获取图像的视觉质量。从观察到的图像中去除噪声是各种图像处理和计算机视觉任务的一个重要步骤。图像去噪的目的是从遵循图像退化模型的噪声观测值中恢复出不含噪声的图像,因此研究优化图像去噪算法具有重要意义。小波变换具有低熵性、多分辨分析、去相关等优点,基于小波变换的去噪算法得到了大量研究。1995年Donoho 等提出对小波系数进行阈值处理来进行图像去噪[1],此后小波阈值去噪算法开始发展[2-3]。小波阈值去噪算法面临的问题主要在于阈值的选取,如果选取的阈值过小,会将一部分噪声当成图像信息保留下来;如果选取的阈值过大,图像中的一些信息特征会被滤除,造成图像失真。Candes 和Donoho 在2000年提出了脊波变换,此后还出现了局部脊波变换和曲波变换,弥补了此前一些算法的不足之处[4-6]。2003年Portilla J 等提出的使用混合高斯模型在小波域去噪[7],该算法在当时取得了良好的去噪效果,近年来小波变换在图像处理领域应用相对广泛[8-10]。基于小波变换的去噪算法往往会破坏小波系数之间的空间关系,甚至影响尺度间和尺度内小波系数的相关性,正交小波变换还会导致图像失真的伪吉布斯现象,这些都会影响算法的去噪性能。
近年来深度学习受到相关研究人员的广泛关注,并逐渐成为互联网大数据以及人工智能的一个热潮,卷积神经网络是人工神经网络与深度学习相结合,通过反向传播算法训练卷积神经网络中的权重,从而实现深度学习的方法。这为图像去噪提供了新思路。基于深度学习的去噪算法也在不断发展[11-17],Harmeling S 等提出了基于MLP的去噪算法[12],Zhang K 等提出了基于残差的去噪算法[13-15],基于深度学习的去噪算法凭借自身的优势取得了相对较好的去噪效果。但基于深度学习的去噪算法是从大量数据中提取特征和拟合非线性函数,因此往往面临着参数量巨大、网络层数过深、调参难度大、泛化能力差等问题,这些算法都是将整幅图像输入网络进行去噪,会造成相对较多的图像失真。基于小波变换图像去噪算法[18-20]则是将图像的分量输入网络,能有效减少图像的失真。本文基于小波变换和卷积神经网络的优势提出了一种性能优良、耗时少的算法。该算法不同于其他算法直接输入图像进行训练,而是将图像进行尺度为1 的小波分解,得到高频分量和低频分量分别输入网络进行训练,使用平稳小波变换避免了空间信息损失,且在训练中使用残差网络,只学习残差信息,可以避免使用过深的网络结构,加快网络的收敛,使用尺寸和数量较小的卷积核来降低计算复杂度,减少参数个数。
1 相关理论
1.1 平稳小波变换
具有平移不变性的平稳小波变换能较好抑制正交小波变换导致图像失真的伪吉布斯现象,已广泛应用于红外图像去噪。基于平稳小波变换的去噪算法,通常是先进行平稳小波分解,得到与图像大小相同的高频和低频分量,其中对于高频分量可采用阈值法等估计小波系数,再通过平稳小波逆变换得到去噪后的图像。通常平稳小波分解得到的各小波系数在尺度内和尺度间具有很强的相关性,这些算法往往难以取得良好的去噪效果。本文算法对图像进行尺度为1 的二维离散平稳小波分解,得到一个低频分量和3 个不同方向上的高频分量:
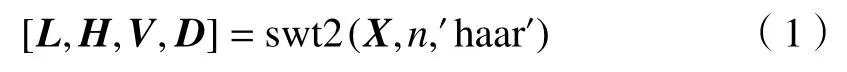
式中:X表示待分解图像;n表示分解尺度;L表示图像经二维离散平稳小波分解后得到的低频分量;H表示水平方向高频分量;V表示垂直方向高频分量;D表示对角方向的高频分量;′haar′表示小波分解时使用haar 基。小波分解在空间比、方向和频率范围方面使图像得以多尺度表示。我们使用小波多尺度表示回归特征,训练用于图像去噪的多重卷积神经网络。基于一级小波分解的训练框架可训练4 个CNN,每个CNN 旨在回归原始图像的多尺度表示之一。我们通过将分解后的低频分量和高频分量分别输入到多个网络中来获得对应的预测分量然后将上述分量使用平稳小波逆变换来获得最终的预测图像,这一过程可以表示为
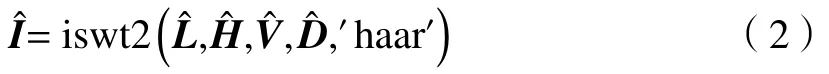
式中iswt2表示小波逆变换。
1.2 残差学习
CNN 的残差学习[21]最初被提出来解决卷积神经性能下降的问题,即随着网络深度的增加,甚至训练精度也开始下降。残差网络学习了残差映射,利用这种残差学习策略,可以容易地训练极深CNN 并提升网络的精度,优化算法性能。一般算法的输入是噪声观测图像y=x+n,其中x表示原始图像,n表示加性噪声,例如判别去噪模型MLP[12]和CSF[22]旨在学习映射函数F(y)=x来获得预测图像。残差学习旨在学习映射R(y)=n,只学习噪声图像和原始图像间的残差,不学习它们共有的信息。残差学习的策略可以很大程度上提升算法效率,训练过程中加快网络的收敛。
2 结合小波变换与残差网络的去噪算法
2.1 网络结构
本文提出的网络框架主要包括4 个结构完全相同的残差网络,除最后一个卷积层外,每个卷积层后都有线性修正单元激活函数ReLU 作为激活函数。完整的网络结构如图1所示。每个残差网络都包含2 个残差块,每个残差块由2 个完全相同的卷积层构成,如图1中的橘色模块。红色虚线框内的网络结构借鉴SRCNN[23]结构,3 个卷积层使用的卷积核大小分别为9×9,1 ×1,5×5,使用的卷积核个数分别为64,32,1。绿色虚线框内的每个卷积层均使用大小为3×3的卷积核,绿色虚线框内最后一层卷积核数目为1,其他层的卷积核数目均为64。红色虚线框内的网络已经达到收敛,主要作用在于去除不同方向上高、低频分量中的噪声。绿色虚线框内的残差网络主要作用在于对高、低频的纹理细节信息进行增强。
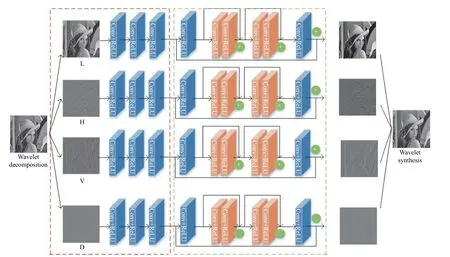
图1 网络结构Fig.1 Structure diagram of proposed network
2.2 算法流程
本文提出的算法流程如图2所示。训练过程中将原始图像裁剪为大小相同的图像块,然后将这些图像块进行非下采样的小波分解,将原始图像块加上噪声进行同样的小波分解,将分解后的图像信息对应起来输入到事先设计好的网络中,通过损失函数来进行反向调节参数,最终达到网络收敛。测试阶段,将一幅含有噪声的图像输入网络,可直接获得一幅预测的清晰图像。本文算法采用均方误差损失函数:
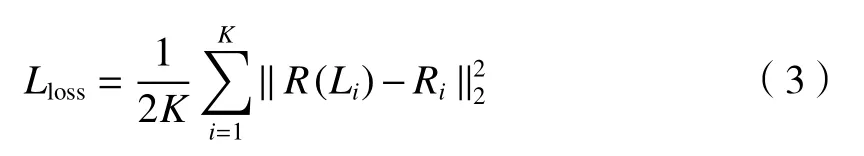
式中:Lloss为损失值;Li表示第i幅输入图像的低频分量;R(Li)为网络的输出;Ri表示实际残差;K为网络进行一次迭代训练输入的图像块数量,实验中取K=64。其余3 个网络使用与第一个网络相同的损失函数,将Li替换为对应的高频分量即可。

图2 去噪算法流程Fig.2 Flow chart of denoising algorithm
3 实验与结果分析
实验训练的数据集为BSDS68 自然图像集,本文采用ADAM 算法对损失函数进行优化,参数beta1 为0.9,参数beta2 为0.999。本文的实验结果皆为100 000 次迭代,学习率为固定值0.001。实验仿真的计算机硬件配置为TntelCorei5-7300 与Nvidia GeForceGTX1060,操作系统为Windows10,使用Caffe 深度学习框架来训练神经网络,该框架支持GPU 运算,用于测试的软件为Matlab R2017a。
常用的图像去噪的评测标准包括主观评价和客观量化。主观评价即人为观测图像,评定输出图像的质量。本文采用两项评价指标对实验结果进行量化:峰值信噪比(PSNR)和结构相似性(SSIM)。PSNR 是一种全参考的图像质量评价指标,它是基于对应像素点间的误差,即基于误差敏感的图像质量评价指标。两幅图像间的PSNR 值(单位:dB)越高,则去噪后的图像相对于原始图像的失真越少。PSNR 的计算公式如(4)式和(5)式:
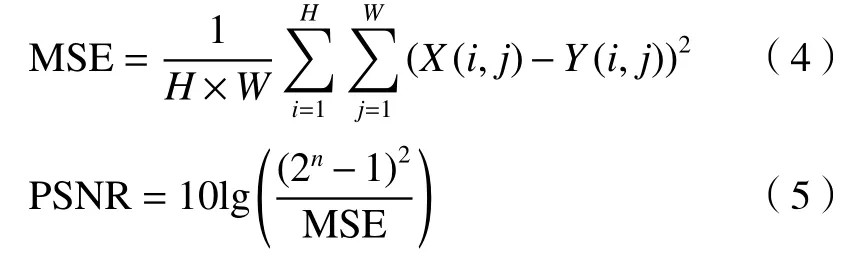
式中:X(i,j),Y(i,j)表示像素矩阵;H和W分别表示图像的高度和宽度;n取值为8。SSIM 也是一种全参考的图像质量评价指标,它分别从亮度、对比度、结构三方面度量图像的相似性,值越接近1,去噪图像与原始图像的相似度越高。SSIM 的计算公式如下式:
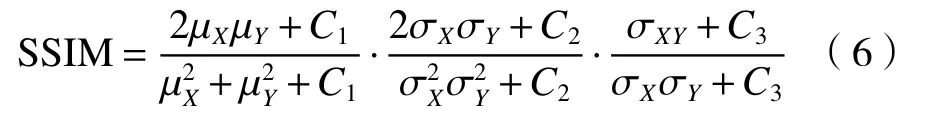
式中:µX和 µY分别表示图像X和Y均值;σX和 σY分别表示图像X和Y的方差;σXY表示两幅图像的协方差,C1,C2,C3为3 个常数。
3.1 不同算法处理结果对比
本文选取的对比算法有中值滤波(median filter,MF),基于小波的软阈值去噪(soft thresholding,ST)[3],EPLL[18],NCSR[19],WNNM[20],用于测试的图像随机选取自set5,set14[13]和set12[14]。噪声水平为σ=25时,我们选取4 幅图像进行视觉效果对比,如图3所示。可以看出,中值滤波去噪以及软阈值小波去噪效果比较差,WNNM[20]算法模糊较为严重。红线框内对应绿线内的局部放大,从局部放大的细节来看,本文算法的视觉效果优于所对比的其他 算法。

图3 不同算法去噪效果对比Fig.3 Comparison of denoising performance with different algorithms
表1是6 幅添加了 σ=25的高斯白噪声的测试图像经不同算法处理后的PSNR 值,本文算法的PSNR 均值可以达到28.93 dB。本文算法处理后的图像有5 幅的PSNR 值均高于其他对比算法,PSNR的均值相较于对比算法提升了0.45 dB~6.87 dB。表2是6 幅测试图像经不同算法处理后的SSIM值,其中有4 幅图像的SSIM 值高于其他算法。表3是不同算法处理这6 幅图像的平均耗时,虽然EPLL[18]和NCSR[19]也能达到相对较好的处理结果,但平均耗时远远超出本文算法。

表1 不同算法实验结果的PSNRTable1 PSNR of experimental results with different algorithms dB
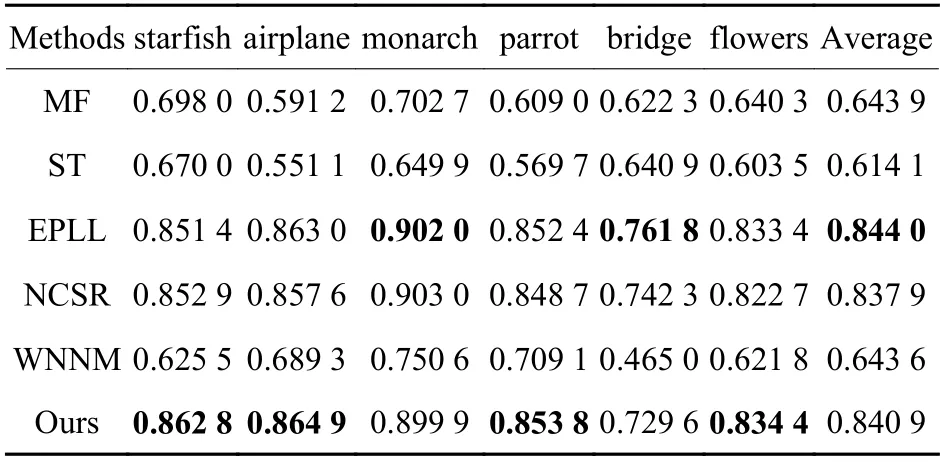
表2 不同算法实验结果的SSIMTable2 SSIM of experimental results with different algorithms

表3 不同算法实验结果的平均耗时Table3 Average time of experimental results with different algorithms
当噪声水平为σ =50时,我们选取lena,peppers,baby,bird 4 幅图像进行视觉效果对比,如图4所示。整体来看,NCSR[19]可以达到与本文算法相当的视觉效果,但从局部放大的细节信息来看,经本文算法处理过的图像的纹理细节更加清晰,peppers和bird 的处理结果尤为明显。
表4是6 幅添加了标准差为50 的高斯白噪声的测试图像经不同算法处理后达到的PSNR 值,本文算法处理后的图像有5 幅的PSNR 值均高于其他对比算法。PSNR 的均值相较于对比算法提升了0.31 dB~8.16 dB。表5是6 幅测试图像经不同算法处理后的SSIM 值,其中有4 幅图像的SSIM值高于其他算法,平均值可达到0.808 0。

图4 不同算法去噪效果对比Fig.4 Comparison of denoising performance with different algorithms

表4 不同算法实验结果的PSNRTable4 PSNR of experimental results with different algorithms dB
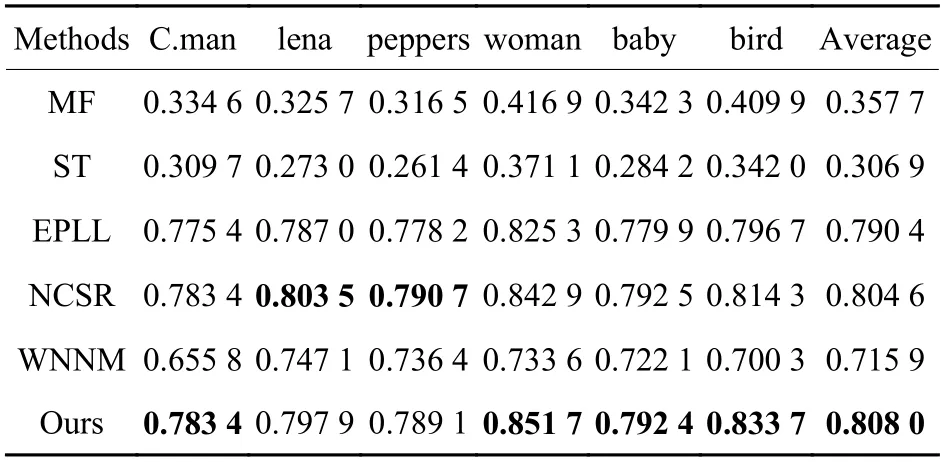
表5 不同算法实验结果的SSIMTable5 SSIM of experimental results with different algorithms
3.2 对自然噪声的去噪
在实验中我们发现本文所提算法对未参加训练的自然噪声也有很好的降噪效果,图5为6 幅来自数据集RNI6[24]带有自然噪声的图像,红色框线内对应绿线框内的局部放大信息,噪声对图像质量影响较为严重。图5是经本文算法处理后的图像,不仅有效去除了噪声,而且图像纹理细节完整。由于该数据集只有噪声图像,未提供原始清晰图像,所以不再计算PSNR 和SSIM.
3.3 对遥感图像的去噪
随着航空航天通信技术的发展,人们的空间概念得到了极大的拓展,基于计算机技术、图像处理技术、对地观测技术而发展起来的遥感数字图像相关技术也随之得到了前所未有的关注与发展。但是在实际应用中,遥感图像的获取与传输非常容易受到外界噪声的干扰,从而使得整个图像所包含的噪声增大,质量降低,增大遥感图像的分析与处理难度,在遥感图像应用前对其进行去噪具有重要意义。本文选取UCMerced_LandUse 遥感图像集中不同场景下的5 幅图像进行去噪,实验结果如图6所示。

图5 本文算法对自然噪声图像的处理结果Fig.5 Image denoising results of real noisy images based on proposed algorithm

图6 本文算法对遥感图像的去噪结果Fig.6 Image denoising results of remote sensing image based on proposed algorithm
4 结论
结合平稳小波变换和深度学习的优势,提出了一种泛化能力较强的去噪算法。其特点有:1)利用平稳小波变换和残差学习的组合优势;2)使用结构较为简单的卷积神经网络,计算复杂度低,参数数量较少,避免出现梯度爆炸;3)所提算法相较于一般算法泛化能力较强,适用于自然噪声,以及遥感图像在成像或传输过程中产生的噪声。通过仿真实验对所提算法的去噪效果进行评估,与传统的中值滤波去噪算法以及软阈值小波去噪等算法相比,本文算法能达到较好去噪效果的同时,还较好地保持了图像的纹理细节信息,同时具有低耗时性的优良性能,在主观视觉效果和客观评价指标上均优于对比算法。本文算法可以为后续的图像处理工作提供有效的预处理,具有一定的实用价值。今后将对卷积神经网络进一步训练,提升算法的去噪性能。

