基于正交试验法的梯级水库连溃分析模型参数敏感性研究
翟梦恩
(浙江中水工程技术有限公司湖州分公司,浙江 湖州 313000)
1 研究背景
伴随社会经济与水利水电技术的不断发展演变,梯级水库的开发利用对我国的基础建设以及农业的发展发挥着重要的作用,若梯级水库在运转过程中发生重大的连溃现象,则会对水域下游造成巨大的灾难[1]。因此,在进行梯级水库的建设施工时必须对相关参数信息进行有效的分析。
目前用于梯级水库的相关敏感性研究中使用的方法主要是对单因素以及多因素进行分析。在梯级水库中的敏感性研究最常用的方法便是单因素分析法,通过选择指标数值以及变化参数,并假设研究中其它参数的固定,利用对比基准指标的变化曲线来反馈各项参数的敏感性[2]。但是用此方法具有一定的缺陷,即可使用的参数较少。因此,本研究将采用正交实验的方式对西南某河流流域中的三级梯级水库(即白鹤滩1-溪洛渡-向家坝)为实例,进行梯级水库的连溃模型分析,并对其下游水库的风险情况进行敏感度分析,为水库的溃坝反演以及风险控制对策提供一定的支持[3]。
2 连溃模型分析原理
梯级水库连溃模型的分析包括上游梯级溃堤进程、上游溃堤后水流向下游流经的进程以及下游梯级水库连溃的进程。根据图1显示,在流域上下游的梯级M、N发生了连溃现象,此时可进行连溃进程的计算:

图1 梯级水库连溃展示图
(1) 上游梯级溃堤的进程:水坝M坝在t1时出现溃堤。对此可使用单一梯级水库溃堤水流模型进行分析。由于堤坝溃口的断面处的流量与宽顶堤堰一致,因此可使用相同公式进行计算:

式中:C为断面水流的流量系数,根据相关研究C取值为1.43 m0.5/s;B1为堤坝溃口处断面的宽度,m;H为水库水位的高程,m;Z为堤坝溃口底部高程,m。
堤坝溃口处的水流冲刷进程中溃口的侵蚀率将采用双曲线模型计算[4],计算公式为:
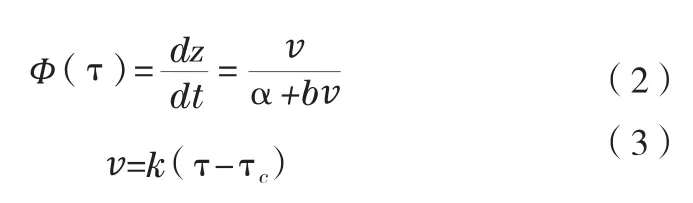
式中:τ为剪应力,MPa;t为进程中的时间,h;α、b为侵蚀率参数;ν为去除临界剪应力之后的剪应力,Pa;k为单位变换因子,其取值为100;Tc为临界剪应力数值,Pa。
(2)下游梯级水库连溃的进程为水坝M溃堤后水流流至水坝N后水流受阻导致水位升高,并出现漫坝最终导致溃堤。
第一阶段:水坝M决堤后水流进入水坝N,导致其水位上涨,这个过程中能量计算公式为:

式中:W为水库的容量,m3;h为水库中的水位,m;q1、q2为水库的入库、出库流量,m3/s。
水位超过坝顶后水流将会溢出,水量的平衡控制方程式则表示为:
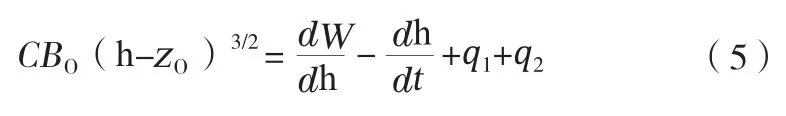
式中:Bo、zo为水流超过坝顶的宽度与相应的高程,m。
对时间步长Δt的水位增量Δh的公式为:
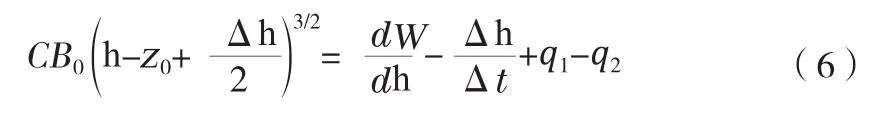
Δh取值较小的情况下可以表达为:
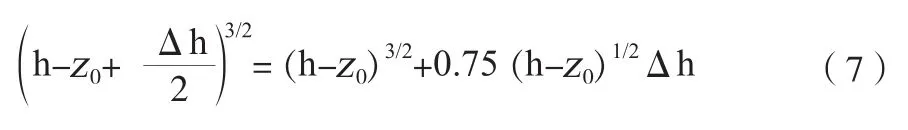
通过公式代入可以得到:

第二阶段:水坝顶部在水流冲刷的作用下形成缺口,成为溃堤的开端,并在连锁反应的条件下发生梯级溃堤。
第三阶段:梯级水库的连溃水流不断向下游冲击。
通过以上的内容可以发现,梯级水库连溃模型中有着较多的影响因素,因此,验证分析中的难点就是模型中相关参数的取值,
3 正交试验
3.1 试验设计
正交试验是以数理统计以及正交原理为基础,在不断的实验中选择具有代表性的参数,并结合正交表以及多因素分析而形成的实验方案[5]。正交试验可以达到均衡分散以及整齐对比的效果,因此,即使通过较少的实验次数也能够准确的反馈出发展规律。
3.2 结果分析
根据正交试验可以得到所需的数值参数,通过分析可以得到数据指标敏感因素。正交试验中结果分析有两种方式:极差分析法和方差分析法。本实验将采用极差分析法进行结果的统计分析[6]:
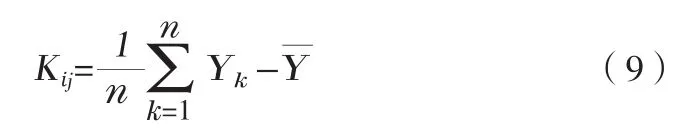
式中:Kij为j在i状态下实验结果的平均值;n为因素j在i状体下的总实验次数;Yk为实验指标的次数;Y为实验结果中的均值。
极差数值Rj的计算公式表示为:

通过极差数值Rj能够呈现出各个数据的敏感因素。
4 梯级水库连溃分析
4.1 工程概况
本文将以西南某河流流域中的三级梯级水库(即白鹤滩2-溪洛渡-向家坝)为实例。工程中白鹤滩水库为一级水库,与溪洛渡相距85.6 km,水库间高差为318.9 m;溪洛渡水库为二级水库,与向家坝相距89.3 km,水库间高差为380.5 m;向家坝为梯级水库中的三级水库。
溪洛渡水库自身不具有削减山洪洪峰流量的功能,向家坝水库包含有溢洪道、泄洪洞等,水坝的泄洪量为8000 m3/s。另外,白鹤滩2 水库设计容量为30.2 亿m3,相较于溪洛渡、向家坝较大,若发生溃堤将会引起下游水库漫顶。为了更好的研究中型、小型、大型三级梯级水库,本文将把白鹤滩2水库的坝高、容量进行适当的调整,在保证其它参数不变的情况下得到白鹤滩1 水库。梯级水库特性见表1。
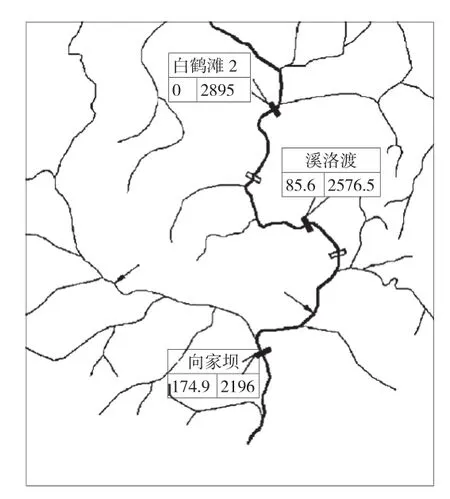
图2 梯级水库平面布置 [水平距离(km);河床高程(m)]

表1 梯级水库特性
4.2 正交试验设计
4.2.1 选取试验指标
本研究结合实际工程案例情况,本次研究将选取一级白鹤滩1水库的溃堤水流量Q、溪洛渡水库的最高水位H1、向家坝水库H2为敏感性因素进行实验的指标分析。
4.2.2 确定试验因素和因素水平
本文根据梯级水库的真实连溃过程选择水流的频率P、侵蚀率参数b以及向家坝水库的初始水位H*进行参数的敏感分析,并在实际参数可行的变化值内设置三个试验标准。正交实验因素水平参数见表2。

表2 正交实验因素水平参数
4.2.3 选择正交表设计试验
本次研究使用L9(34)正交表进行实验,假设最后列为空白列,将试验因素进行随机匹配到正交表中的前三列中,正交表中各个元素均可以对应因素个数及水平匹配到相对照的参数,从而便可以得到模型参数中敏感度正交实验表,且表格中各列均可以对应一个实验策略[7]。
4.3 梯级土石坝数值计算
本研究试验方案中的梯级水库连溃模型将使用梯级土石坝参数进行分析。详细的试验方案:P选值为0(自然频率)、b选值为0.83 mm/s、H*选值为2485 m(防洪限制水位),进行水坝的溃堤参数计算。详细输入参数见表3。

表3 计算中输入参数
白鹤滩1 流量的峰值为127625 m3/s,洪峰时间为12.6 h。当白鹤滩1 水库发生溃堤时,溃决流量过程见图3。二级溪洛渡水库将打开泄洪设施,其正常起调蓄水水位为2685 m,溪洛渡水库出流与水位变化的过程见图4、图5。

图3 白鹤滩1溃决流量过程
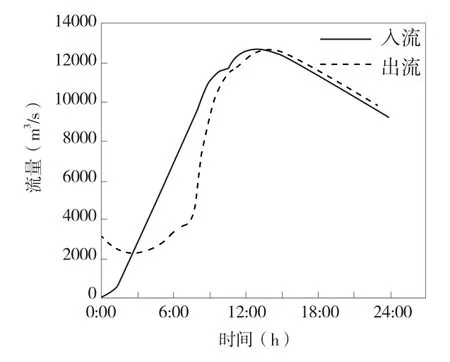
图4 溪洛渡水库出流过程
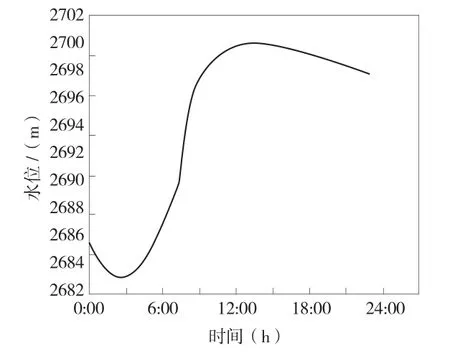
图5 溪洛渡水库水位变化过程
从图5 中可以发现,当白鹤滩1 水坝溃堤后溪洛渡水库的水位为2700 m,但溪洛渡水坝高度为2690 m,此时溪洛渡水库则会发生漫顶,时间为7.3 h。由于白鹤滩1 水库的库容较小,向家坝不需要提前开启泄洪设施,只需要在一级、二级水库溃堤后开启泄洪设施即可。向家坝正常起调蓄水水位为2485 m。向家坝水库出流与水位变化的过程见图6、图7。
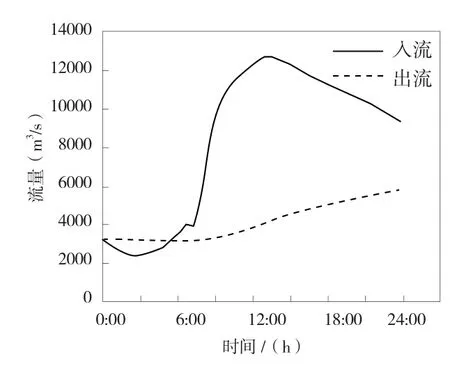
图6 向家坝水库出流过程
从图7 中可以发现,向家坝水库在白鹤滩1、溪洛渡水库溃堤后的水位将达到2497.2 m,而向家坝的设计坝高为2510 m,因此,向家坝将不会出现漫顶的情况。

图7 向家坝水库水位变化过程
4.4 敏感性分析
白鹤滩1 水库的决堤流量Q、溪洛渡水库允许最大水位H1、向家坝水库允许最大水位H2,将三项数值带入到正交试验表后三列中,依据实验方案的结果使用极差法进行指标的敏度性分析[8]。
对参数Q相关的影响因素使用极差分析后结果显示各因素对参数Q的敏感为:b>P>H*。参数Q影响因素分析结果见表4。

表4 参数Q影响因素分析结果
对参数H1相关的影响因素使用极差分析后结果显示各因素对参数H1的敏感为:b>P>H*。参数H1影响因素分析结果见表5。

表5 参数H1影响因素分析结果
对参数H2相关的影响因素使用极差分析后结果显示各因素对参数H2的敏感为:H*>P>b。参数H2影响因素分析结果见表6。
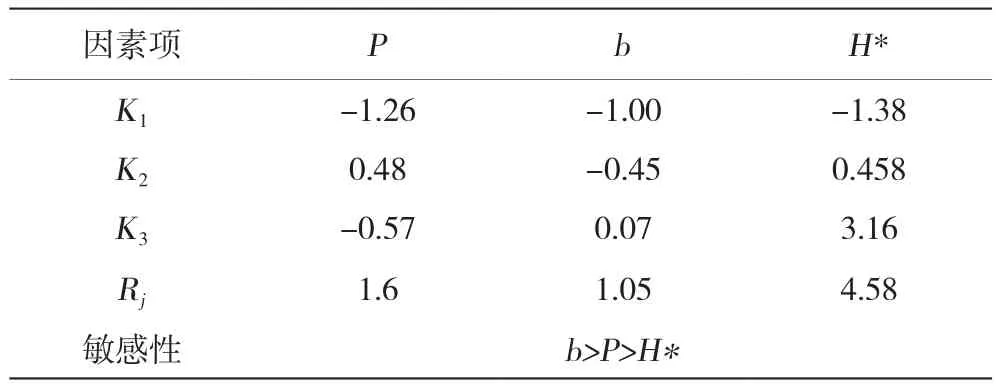
表6 参数H2影响因素分析结果
对各试验指标Q、H1和H2的极差分析结果进行整理后可以发现梯级水库连溃模型中参数b、P对白鹤滩1的溃堤以及溪洛渡水库的最大水位具有较大的影响,且敏感度上b>P,H*对上述两个水库无影响;向家坝水库中敏感性较大的因素为H*(H*>P>b)。
5 结论
采用正交试验对梯级水库的连溃模型进行分析计算,实验结果显示参数b、H*具有较高的敏感性;参数P的敏感性相对较低。因此,在进行相关的实验中应重点考虑敏感参数因素,一次降低实验计算的工作量、增加分析的工作效率,确保反演的精准性,通过本次研究希望为以后的梯级水库连溃分析以及实际工程紧急情况的处理提供指导建议。

