薄板状导体地-井瞬变电磁场数值模拟及晚期响应特征

刘祖鉴，刘诗华，马一行，张博洋

(1.中国自然资源航空物探遥感中心，北京 100083； 2.中国地质调查局 发展研究中心，北京 100037； 3.自然资源部矿产勘查技术指导中心, 北京 100083； 4.中国科学院 力学研究所，北京 100190)

0 引言

地-井瞬变电磁法(surface-borehole transient electromagnetic method，地-井TEM)通常采用地面布设的回线源，供以脉冲电流产生激发场，切断场源后由置于钻孔中的探头接收地层和目标体感应产生的二次场，研究分析二次场特征获取关于井旁(底)目标体的信息。由于地-井TEM主要通过分析响应特征规律进行工作，因此正演模拟成为重要问题：文献[1-2]应用本征环流法计算地-井TEM响应并总结了解释方法，文献[3-5]分别探讨了导电围岩中地-井TEM的响应符号变化、观测结果所受影响及三分量接收信号等问题，文献[6]完成了典型导电介质条件下地-井TEM响应的物理实验，文献[7]介绍了地面与井中TEM的联合应用情况，文献[8-9]研究了TEM的地面与井中数据联合反演方法；国内研究者基于等效涡流等方法论述了地-井TEM解释原理[10-11]，在数值模拟与实际应用方面开展了研究工作[12-14]，并在矿井TEM方面取得了一定成果[15-16]。

地层介质会影响地-井TEM观测结果，接收到的信号受到多种因素制约，响应特征规律较为复杂。瞬变电磁在导电薄板状体中的感应涡流进入晚期后涡流分布状况已经趋于稳定，并按指数规律衰减[2]。在等效数学模型中，多使用本征环流应用于早期和中期的瞬变电磁异常响应计算，而在晚期的计算中，使用等效涡流法更为简便[10-11]，对瞬变电磁野外工作的部署具有一定的意义。所谓“等效涡流”表示分布在异常体内1/N束的本征电流圈，其模拟结果必然与本征环流的响应及幅值相近。使用等效涡流计算简单便捷，可以对勘探施工阶段遇到的临时问题即时分析解释。虽然该方法只能计算2～4块任意组合体和有导电围岩或覆盖层的响应情况，但是仍然可以对过往地质、物性资料进行正演，用来作为前期设计工区如回线大小、剖面长度、点距、发射电流大小等参数的依据；还可利用正演拟合完善后期成果解释等[15-17]。

1 晚期地-井瞬变电磁等效涡流场

本文应用磁偶源TEM数值计算方法，对薄板状体的晚期等效涡流场进行数值模拟(如图1)，分析响应特征规律，为相关研究提供参考。

设长、短边分别为b、a的薄板状导体在发射回线(Tx)产生的近于均匀的一次场激励下，薄板体中心部位会产生一个长、短边分别为0.7b、0.7a的等效涡流，并且位于板状体的中心部位[10]。Tx回线与等效涡流环之间的互感系数为M1，等效涡流环与接收回线(Rx)之间的互感系数为M2，

Tx的某条边l1和等效涡流与其平行的某条边l2之间的互感系数由Neumann formula可得：

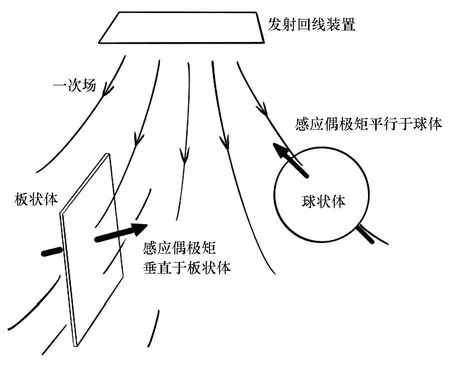
图1 涡流在板状体和球状体中运动的示意Fig.1 Schematic diagram of eddy current movement in plate and spheroid

(1)

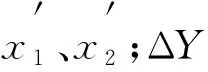
(2)

可以通过16次相互计算得到Tx各个边与等效涡流环各个边的互感系数，相加即可求出Tx与等效涡流环的总互感系数；再用同样的方法计算等效涡流环与Rx之间的互感系数。

依据电路原理可知：

Φ1=I·M1，

(3)

(4)

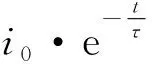
(5)

(6)

式中：H1n(即H1·cosθ)为作用于薄板体的一次场法向分量，H1为一次场，θ为薄板导体与Tx所在平面(一般即水平面)的夹角；S为纵向电导。Rx产生的感应电压为：

(7)

用类似的算法，可以再加上3块板状体的响应值，这4块板的大小、倾角、走向以及电性参数等可以任意改变或组合[10-11]。

2 数值模拟及晚期响应特征

薄板状体的数值模拟采用400 m×400 m的矩形发射线圈，位于板状体的正上方。设置了4种地电模型，表1列出了地电模型的各项参数。

表1 薄板体瞬变电磁数值模拟参数一览Table 1 Parameters of transient electromagnetic numerical simulation of thin plate

地下空间中产生的一次场和二次场均为矢量场，地-井瞬变电磁法为发射源固定、接收点在不同位置观测电磁场响应，因此电磁场的方向，即响应值的“正”、“负”号是研究其规律的一个重要参数，需要明确坐标系来确定异常响应所产生的正负性。参照加拿大CORNE公司地-井TEM坐标系：规定井轴分量向上为正，井陉分量按照右手定则规定正方向，本文试验均为直孔，即为笛卡尔右手坐标系。

图2中的不同钻孔接收水平单板体的异常响应曲线能够准确反映出该地电模型的层状结构特征：钻孔垂直穿过异常体时异常形态为单峰正响应，异常体埋深位置出现极值，随着钻孔偏移距的增大，在异常体边缘位置产生三峰对称正负异常，异常峰值为负异常，位于近矿体侧；随着电磁信号衰减钻孔在远离异常体位置出现单峰负异常。断电延时越短，异常响应的幅值越大，随着时间的增加，异常体二次场电磁强度逐步衰减，不同偏移距的钻孔数据均显示出感应涡流场随着时间增加而逐步扩散的特性。

响应曲线的耦合关系将影响响应特征。图3中当钻孔从矿体中心位置穿过时，异常形态同样为单峰正响应，响应峰值反映出矿体深度位置，与水平板状体的异常特征一致。当钻孔位于异常体边界时，异常出现非对称异常，正异常的幅值与负异常相近。当钻孔离矿体较远时，呈现单峰负异常特征，随着瞬变电磁响应逐步衰减，此时不能识别产状的变化。

实际情况中，矿床的形成往往是由多个板状体组合在一起的。由图4可以发现，当钻孔垂直穿过异常体中心位置及远离矿体位置时，组合体异常范围反映了4块异常体的埋深，同单板异常体一样，表现为单峰正异常，但曲线变化较为平缓，幅值较单板状体有所增大。当钻孔位于矿体边缘位置时，产生三峰对称正负异常，异常峰值为负异常，异常曲线幅值平缓，组合异常体的响应曲线由于受多板状体涡流场电磁耦合的制约作用，并未出现幅值显著增加的情况。

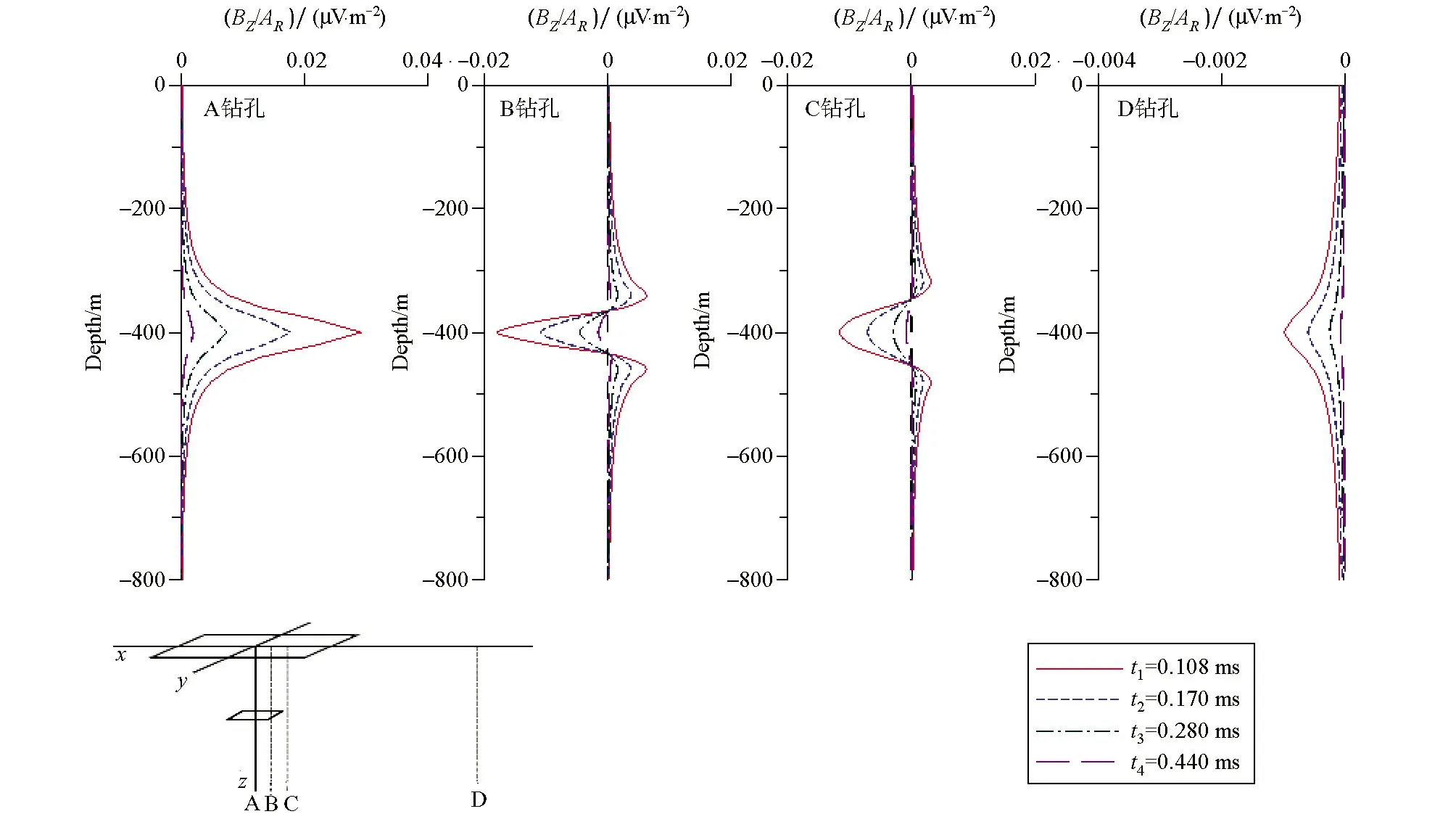
图2 不同钻孔接收水平单板体模型示意及异常响应曲线Fig.2 Surface-hole TEM responses for a conductive plate in different dill-hole

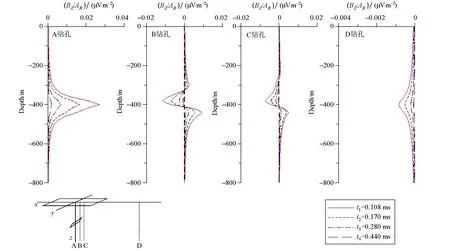
图3 不同钻孔接收倾斜单板体模型示意及异常响应曲线Fig.3 Surface-hole TEM responses for a tilt conductive plate in different dill-hole

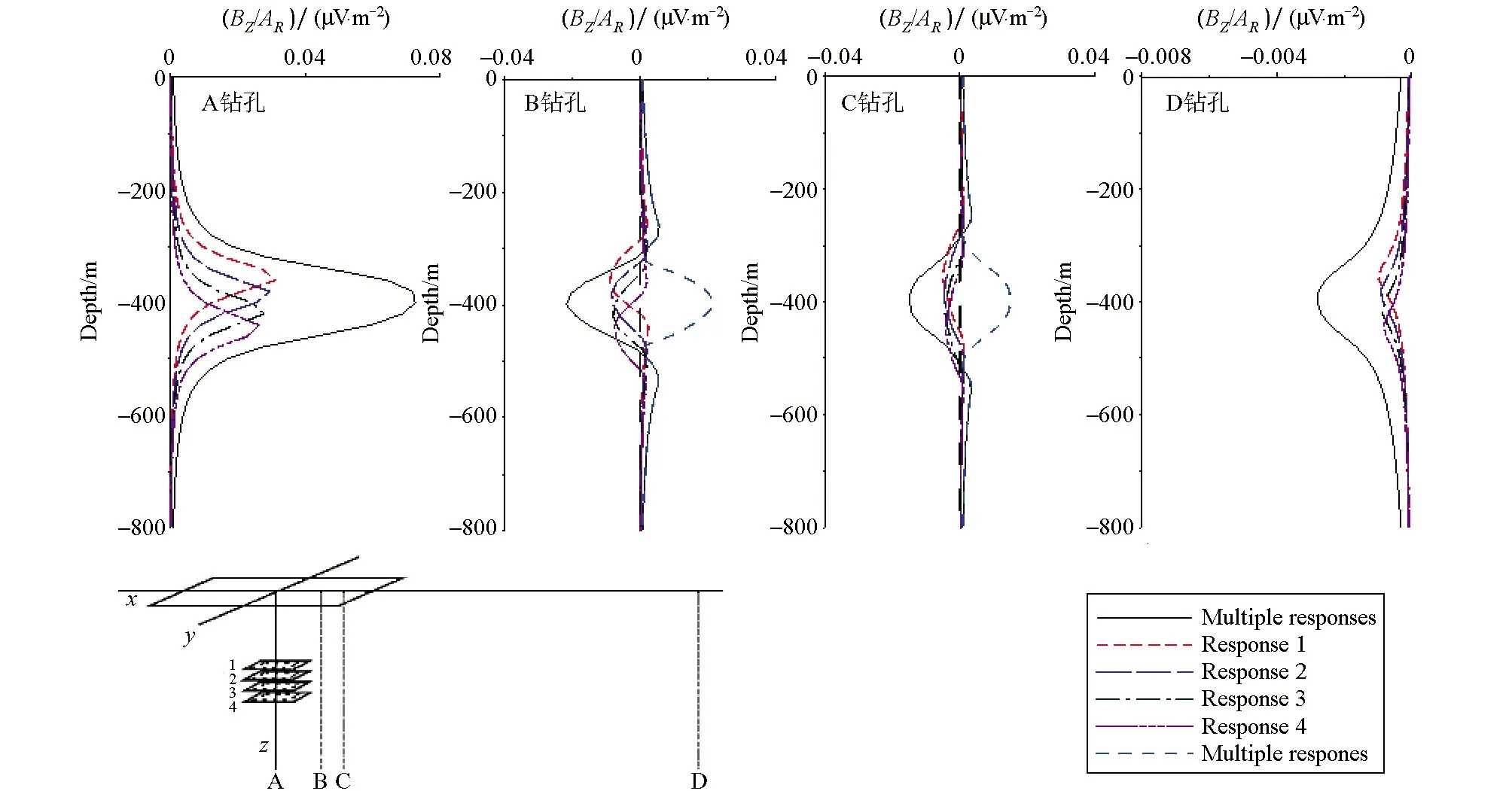
图4 不同钻孔接收水平多板体纵向组合模型示意及异常曲线Fig.4 Surface-hole TEM responses for model of multiple conductive plates in different dill-hole

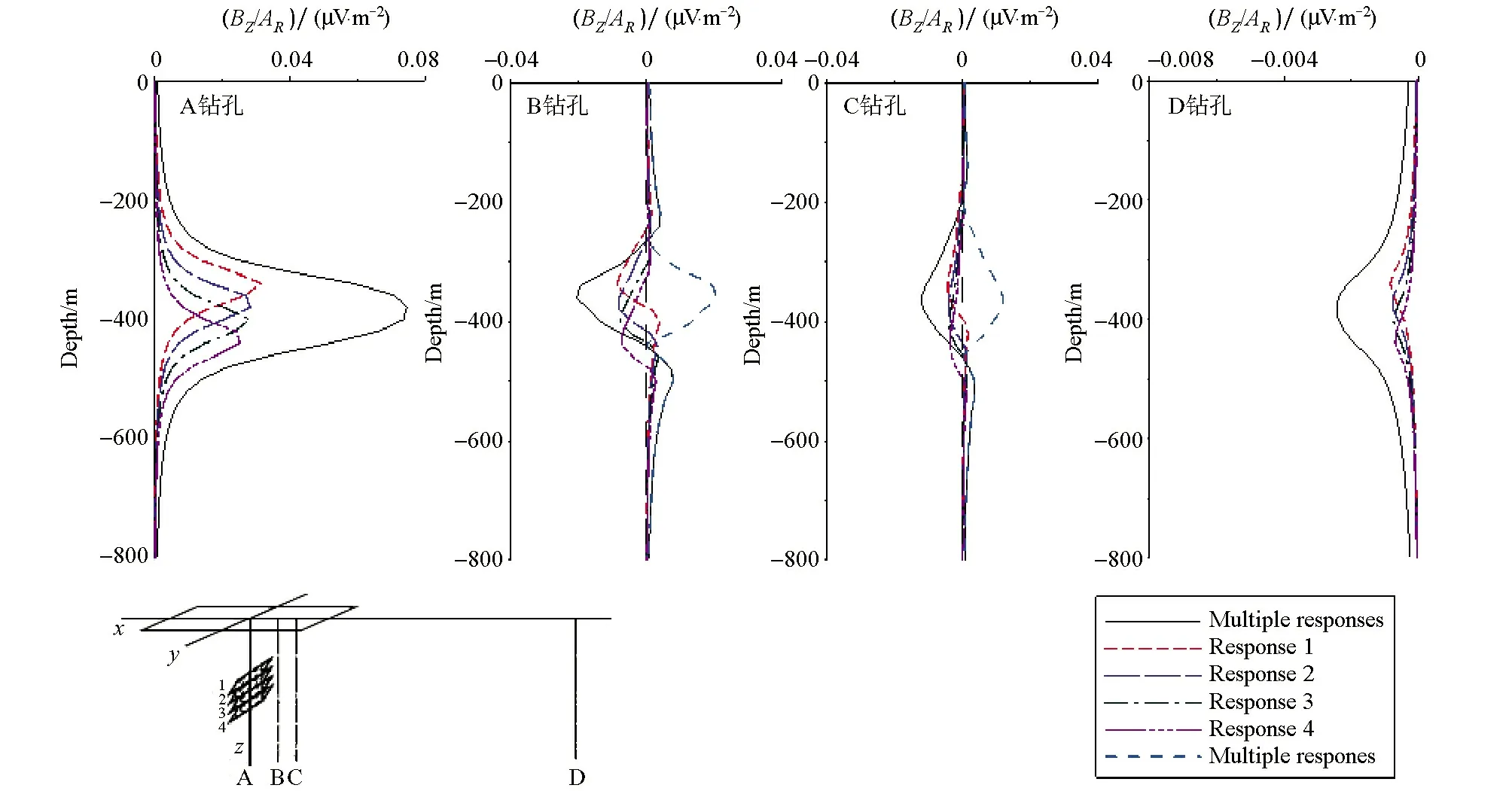
图5 不同钻孔接收倾斜多板体纵向组合模型示意及异常曲线Fig.5 Surface-hole TEM responses for model of multiple tilt conductive plates in different dill-hole

由图5可以发现，当钻孔垂直穿过异常体中心位置及远离矿体位置时，响应曲线满足水平组合体异常特征规律；当钻孔位于矿体边缘位置时，出现非对称异常，且近异常体侧的负异常远大于远离异常体侧的正异常，幅值并未显著增大，曲线变化较平缓。这是由于组合异常体的响应虽然同样受电磁耦合作用影响，但其组合体的耦合作用远强于因单板状体倾斜而产生的耦合作用，导致曲线不对称性并未如倾角为45°单板体显著。

3 结论

本文利用等效涡流方法进行了4种模型在不同产状和钻孔偏移距情况下的瞬变电磁数值模拟，通过分析其晚期响应特征，得出以下结论：

1)在断电延时较短时，对于导电体异常响应较大，异常形态为单峰正异常响应；随着时间推移，电磁响应逐步衰减。

2)当钻孔从矿体中心位置穿过时，异常形态为单峰正异常响应，响应峰极值位于矿体埋深位置。

3)当钻孔位于靠近矿体边缘位置穿过：矿体产状为0°时，产生三峰对称正负异常，异常峰值位于近矿体侧的负异常；产状为45°时，异常形态出现非对称正负异常，矿体顶侧出现负异常，底侧出现正异常，顶侧峰值强于底侧峰值。

4)当钻孔远离矿体时，瞬变电磁响应逐步减弱，表现为单峰负异常，此时不能识别产状的变化。

5)相同产状条件下，组合板状体异常幅值较单板状体异常的幅值增大，其异常形态符合单板状体的异常响应特征。