粘弹介质勒夫波频散曲线研究及应用

张保卫，董晋，吴华

(1.中国地质科学院 地球物理地球化学勘查研究所，河北 廊坊 065000;2.国家现代地质勘查工程技术研究中心，河北 廊坊 065000;3.铁道第三勘察设计院集团有限公司，天津 300251;4.长安大学 理学院，陕西 西安 710064)

0 引言

1887年，英国科学家Rayleigh[1]证明了瑞利波的存在。此后，科学家们利用瑞利波在层状介质中具有很强的频散特性，将其应用于岩土分层、地下空洞探测、场地液化度评价等工程质量检测中。经过多年的发展，人们对瑞利波的波动方程解析与频散曲线正反演研究更加深入，瑞利波勘探也因此得到了广泛应用。实际上多层介质中不仅仅存在瑞利波这一种面波，还存在一种由SH波相干产生的勒夫波面波。1911年英国科学家Love[2]提出如果在一种弹性介质上覆盖着另一种一定厚度的弹性介质，则在弹性半空间的表面附近及覆盖层内存在一种SH型面波，即为勒夫波。其产生机制中无纵波参与，因此勒夫波的频散特性仅与横波速度有关，这一性质可大大减少反演的非唯一性，即用较少的反演参数就可以得到更精确、更可靠的横波速度。Xia等[3]通过大量的理论和实验数据证明了勒夫波多道分析法相对于瑞利波法具有频散曲线求解更加简单、数据信噪比更高、频散曲线反演对初始模型的依赖程度更低等优点。然而在近地表地球物理勘探领域中，与瑞利波相比，人们对勒夫波的重视程度较低。因此，有必要进一步开展勒夫波正反演研究，为浅层结构探测提供有效的方法技术支持[4]。

勒夫波勘探作为一种新兴的探测手段，已开始在众多领域得到应用和推广，但还存在一些亟待解决的问题，比如粘弹介质情况下勒夫波理论频散曲线的计算和反演。我们知道，在实际的地球模型中，地层介质是具有粘弹性的，尤其是近地表第四系软土对地震波的吸收衰减作用更为显著。在粘弹介质瑞利波频散曲线研究方面有多位学者开展了卓有成效的研究[5-8]，证明了介质的粘弹性对会对瑞利波频散曲线产生较大的影响。同理可知，介质的粘弹性同样会对勒夫波频散曲线产生一定的影响。因此，开展粘弹介质勒夫波理论频散曲线研究具有重要的现实意义。

近十几年以来关于勒夫波的研究越来越受到广大学者的不断关注，2003年Winsborrow等[9]利用勒夫波数据获取了海洋沉积物的“地质—声学特性”的横向变化情况。2005年，Wang等[10]研究了在线性变化非均匀流体饱和多孔层状半空间中的勒夫波传播情况。2006年Safani等[11]实现了低速层情况下勒夫波的模拟和反演。2008年马志杰等[12]对勒夫波相速度频散曲线敏感性进行了比较分析。2010年，Luo等[13]基于标准交错网格有限差分法研究了完全弹性介质中3种典型地层的勒夫波频散特征。2012年，夏江海等[3]提出了多道勒夫波分析法(multichannel analysis of Love waves)，反演获得了浅地表横波速度。2013年，夏江海、尹晓菲[14]采用弱衰减条件下勒夫波衰减系数的近似公式[15]反演得到了地层横波速度品质因子，避开了求解勒夫波复数频散方程问题。2016年，谢俊法等[16]采用无分裂复频移卷积完全匹配层边界条件，进行了粘弹介质的勒夫波数值模拟。2017年，伍敦仕等[17]对粘弹介质勒夫波频散问题的统一解问题进行了研究，发现地下存在低速夹层时粘弹介质勒夫波频散曲线存在交叉现象。对于勒夫波的研究不少学者都作了卓有成效的工作，但在介质的粘弹性对勒夫波理论频散曲线有何影响方面的研究仍未见广泛开展。笔者拟通过求解频散方程获得勒夫波理论相速度频散曲线，采用高阶有限差分模拟得到粘弹介质情况下的勒夫波单炮记录并从中提取对应的频散曲线；对理论模型提取得到频散曲线与理论频散曲线开展对比研究，并进一步分析粘弹性介质对勒夫波频散曲线的影响；然后对频散曲线进行反演得到地下横波速度结构以验证方法的可行性和有效性；最后通过野外试验来进一步验证本文方法的实际应用效果。

1 粘弹介质勒夫波频散曲线计算

1.1 二维均匀粘弹介质勒夫波方程

如图1，考虑一个水平均匀介质，质点v是沿y方向位移，勒夫波沿x方向传播。勒夫波方程为：

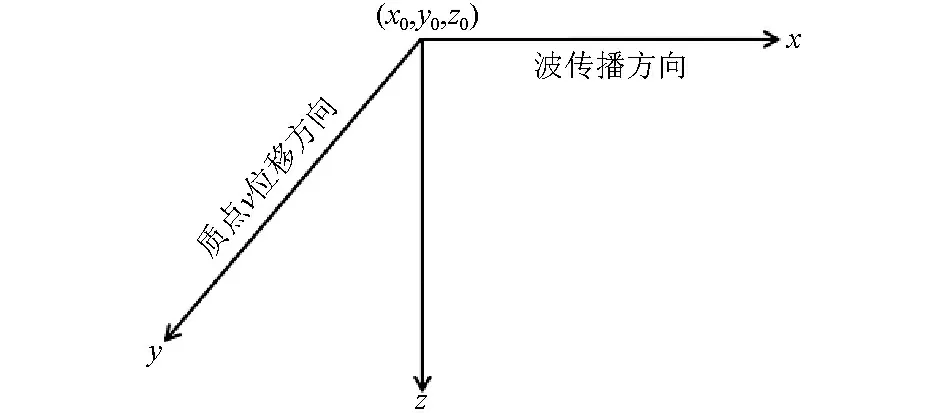
图1 水平均匀介质模型Fig.1 Horizontal uniform medium model

其中，υ表示质点位移，ρ为介质密度，μ*表示复剪切模量，t表示时间，x、y、z分别为三个坐标轴方向。

用分离变量法将式(1)分离为3个独立变量函数:

υ(x,z,t)=R(x)L(z)T(t) 。

(2)

将式(2)代入式(1)分离变量后，3个独立变量函数对应的解为[18]：

(3)

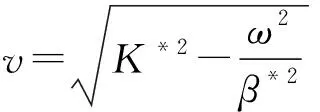
当波沿x正方向传播，a2和b1为0，令a1=b2=1得：

υ(x,z,t)=L(z)R(x)T(t)=(sde-vz+suevz)ei(K*x-ωt)。

(4)

将水平波数分别用其实部和虚部表示，令K*=Kr+iKi代入式(9)得：

υ(x,z,t)=L(z)R(x)T(t)=L(z)e-Kixei(Krx-ωt), (5)

复波数的虚部Ki代表了空间上的衰减系数。

1.2 二维层状粘弹介质勒夫波方程

在上一节均匀粘弹介质中，我们定义的T(t)和R(x)与深度无关，而对于多层介质只需把L(z)与厚度的关系扩展到多层介质即可。对于一个覆盖在均匀半空间上的粘弹层状介质，在每一个分界面的两侧应满足位移和应力连续的条件，位移项lm,j(z)表示在深度z处第j层的L(z)的值，同一处的应力τz,y可表示为:

(6)

下标m和s分别表示位移项和应力项，由式(4)得：

μ*v(-sde-vz+suevz)ei(k* x-ωt)。

(7)

将位移项和应力项合并为一个位移—应力向量：

(8)

在两个相邻层j和j+1的分界面上应力相等，因此lj(z)=lj+1(z)。

设传递矩阵P(za,zb)为位移—应力向量在任意两深度za和zb之间的耦合关系，有：

l(za)=P(za,zb)l(zb) 。

(9)

当z=0时，即在自由界面处，由Dirichlet边界条件可知，应力τy,z=0，用下角标j表示第j层介质的底界面，因此，自由界面为z0，第1层介质的底界面为z1，第n层介质的底界面为zn。

对于一个n层介质模型，自由界面与第n层介质的底界面(也是半空间介质的顶界面)之间的关系可由传递矩阵表示为：

l(zn)=P(zn,z0)l(z0) 。

(10)

在均匀半空间中无上行波，因此均匀半空间对应的传递矩阵与其上部的层状介质不同。定义均匀半空间对应的传递矩阵为P(z∞,zn)，而半空间中上、下行波的位移振幅与地表位移—应力向量之间的关系可定义为：

(11)

根据分离变量后函数L(z)对应的方程，并将式(6)用位移项lm,j和应力项ls,j来表示可得[18]：

(12)

将式(12)写成矩阵形式，有：

(13)

对于某一单个地层，上述一阶线性微分方程的解即为该层的传递矩阵[18]：

P(zj,zj-1)=e(zj-zj-1)A=ehjA,

(14)

其中，hj为第j层的厚度。

根据传递矩阵的性质，P(zn,z0)可由每一层的传递矩阵按链式法则相乘得到：

P(zn,z0)=P(zn,zn-1)P(zn-1,zn-2)…P(z2,z1)P(z1,z0) 。

(15)

为方便计算，可对式(14)中的矩阵A进行奇异值分解得[18]：

由式(11)和式(15)可得最终的勒夫波方程为：

(17)

将自由界面应力为零以及半空间无上行波等边界条件应用于式(17)可得：

(18)

若使式(18)成立，则有B2,1=0。因此，B2,1可作为计算勒夫波频散曲线的目标函数，既给定水平波数K*的值来寻找使得目标函数为零的奇异值v。

2 模型试算

本文选用具有代表意义的三层速度递增模型探讨介质的粘弹性对频散曲线的影响。如图2所示，模型大小为100 m×50 m；第1层介质横波速度为150 m·s-1，密度为2 000 kg·m-3，厚度为5 m；第2层介质横波速度为300 m·s，密度为2 000 kg·m-3，厚度为5 m；第3层(半空间)介质横波速度为450 m·s-1，密度为2 000 kg·m-3。震源为雷克子波，主频25 Hz。模拟计算采用交错网格有限差分并行算法[19]，网格间距Δx=Δz=0.25 m，炮点位于地表0 m处，道间距2 m，最小偏移距0 m，48道接收；采样间隔Δt=0.1 ms，采样长度0.8 s。分别对完全弹性介质、粘弹介质品质因子Q=50和Q=20三种情况进行数值模拟，得到相应的单炮记录，同时采用τ-p变换与相移联合方法[20]提取模拟记录的勒夫波频散曲线，并与采用上一节方法得到的理论频散曲线进行对比分析，探讨品质因子不同时频散曲线的变化特征。

图2 三层速度递增模型Fig.2 Three-layered model of increasing velocity

图3分别是完全弹性介质、粘弹介质品质因子Q=50和Q=20三种情况下计算得到的勒夫波单炮模拟记录(水平分量)。图4是完全弹性介质、粘弹介质品质因子Q=50和Q=20三种情况下第25道和第48道单道记录波形对比。由图3和图4可以看出，随着介质粘弹性的增强，勒夫波振幅衰减越来越严重，尤其是远偏移距处信号的高频成分衰减更为严重。在利用勒夫波地震记录提取得到的频散曲线进行反演时，如不考虑介质粘弹性的影响，显然会给反演结果带来一定的误差。

a—完全弹性介质;b—粘弹性介质Q=50;c—粘弹性介质Q=20a—completely elastic medium;b—viscoelastic medium with Q=50;c—viscoelastic medium with Q=20图3 完全弹性介质与粘弹介质(Q=50、Q=20)单炮模拟记录(水平分量)对比Fig.3 Comparison of the wave field record (horizontal component) for completely elastic medium and viscoelastic medium(Q=50、Q=20)

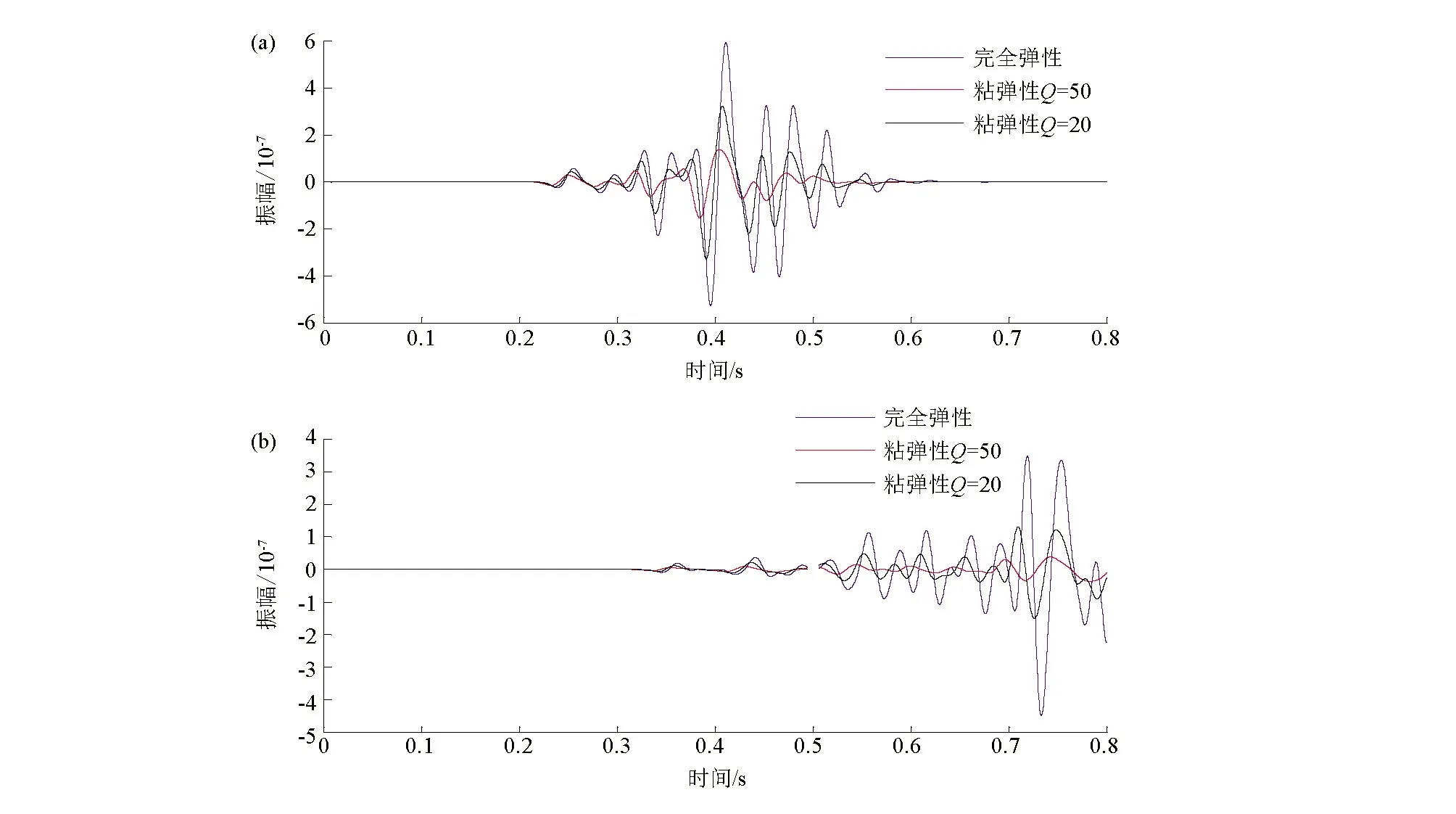
a—第25道波形对比;b—第48道波形对比a—waveform comparison of the 25th trace;b—waveform comparison of the 48th trace图4 完全弹性介质与粘弹介质(Q=50、Q=20)单道记录(水平分量)波形对比Fig.4 Comparison of single trace (horizontal component) waveform for completely elastic medium and viscoelastic medium(Q=50、Q=20)

图5分别是完全弹性介质、粘弹介质品质因子Q=50和Q=20情况下利用τ-p变换与相移联合方法从勒夫波单炮模拟记录中提取得到频散能量分布图，彩色曲线分别为由式(26)计算得到的理论勒夫波频散曲线，可以看出，各模式的勒夫波理论频散曲线与其炮记录提取得到的频散能量极大值吻合得较好。频散曲线的高频极限趋近于最上层介质的横波速度(150 m·s-1)，而低频极限趋近于最下层介质的横波速度(450 m·s-1)。

图6是完全弹性介质、Q=50、Q=20时所对应的前三阶理论频散曲线对比图。从图中可知，低频处基阶模式的相速度相差不大，高阶模式的相速度随介质粘弹性的增强(Q值减小)而增加。随着频率的增高，介质粘弹性越强，各阶模式的高频极限收敛速度越大。各模式频散曲线的最低相速度均高于完全弹性情况下的理论相速度，且Q值越小，最低相速度越大。可见勒夫波频散曲线的高阶模式以及各阶模式的高频成分对介质的粘弹性较为敏感。因此，在利用勒夫波频散曲线进行横波速度结构反演时，应考虑介质品质因子Q的影响。

a—完全弹性介质;b—粘弹性介质Q=50;c—粘弹性介质Q=20a—completely elastic medium;b—viscoelastic medium with Q=50;c—viscoelastic medium with Q=20图5 完全弹性介质与粘弹介质理论频散曲线与单炮记录频散能量对比Fig.5 Comparison of theoretical dispersion curve and the dispersion energy in single shot record for completely elastic medium and viscoelastic medium

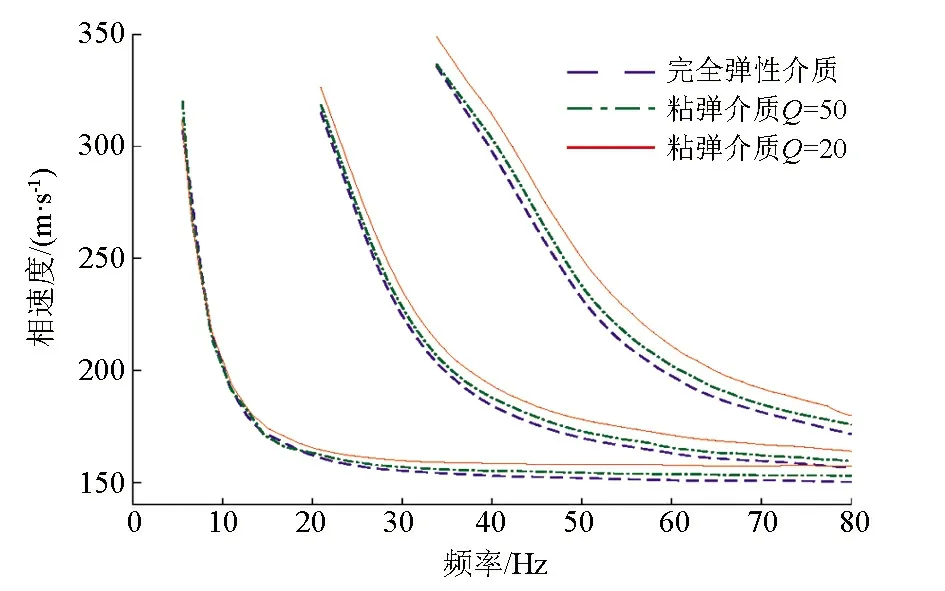
图6 完全弹性介质与粘弹介质理论频散曲线对比Fig.6 Comparison of theoretical dispersion curves for completely elastic medium and viscoelastic medium

现利用粘弹介质品质因子Q=20的频散曲线作为观测数据进行横波速度结构反演，采用最小二乘法反演算法。反演时分别按完全弹性介质和给定真实Q值的粘弹介质进行计算。为验证介质粘弹性对反演结果的影响，反演中层厚度和密度均为已知量，只反演横波速度，反演初始模型选择横波速度为300 m/s的均匀介质，反演结果如图7所示。由图7可看出，当将实际为粘弹性的介质按照完全弹性介质进行反演时，反演结果略大于真实模型的横波速度，原因是由于粘弹性的影响导致其频散曲线在高频段的相速度略大于完全弹性介质的相速度，如果将原本为粘弹介质的频散曲线看作完全弹性介质的频散曲线，势必会对反演结果造成一定的误差。当反演时按照粘弹性频散曲线公式进行计算，给定准确的品质因子(Q=20)，反演所得地层结构的横波速度与其真实值更为接近，反演结果令人满意。

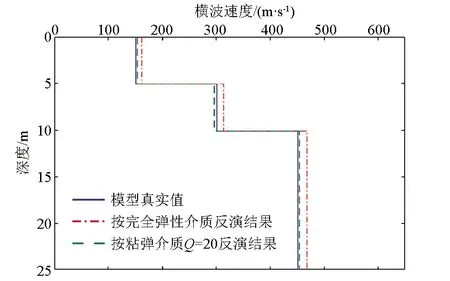
图7 理论频散曲线横波速度反演结果Fig.7 Shear wave velocity inversion results of theoretical dispersion curves

3 野外实际资料处理

为验证方法的野外实际资料处理效果，本文选取了一个人工隧道进行勒夫波探测试验。试验场景如图8所示。隧道宽约6 m，顶面埋深约3 m，底面埋深约6 m。地震测线位于隧道上方的平台上，测线方向垂直于隧道走向。由西向东共布置24个三分量检波器，道间距2 m，最小偏移距4 m。第一道位于测线最西端0 m处，第24道位于47 m处，滚动排列，隧道位于第33～39 m之间。震源采用锤击震源，击震方向垂直于测线，横向击震，炮间距4 m，采样率0.5 ms，采样长度512 ms，每道1 024个采样点，每炮叠加3次，共采集13炮。

图8 野外试验场景Fig.8 Field test scenario

图9是经过预处理后的第一炮野外勒夫波记录以及提取得到的频散曲线。从图中可以看出频散曲线的高频极限趋近于表层介质的横波速度200 m/s，低频极限趋近于最底层介质的横波度500 m/s。因此，反演时可根据频散曲线的高频极限和低频极限事先设置一个速度在两个极限速度之间逐渐递增的初始模型。反演之前采用Xia等[7]的方法提取得到了试验区的品质因子Q平均约为10，然后采用最小二乘法对勒夫波实测频散曲线按粘弹介质Q=10进行反演，由13炮记录反演得到的二维横波速度结构断面图如图10所示。由图10可以看到以第36 m为中心，存在一个明显的低速异常体(速度范围低于200 m/s)，图中红圈为隧道空洞的大致位置，异常体的顶界面与隧道的顶界面基本一致，而底界面与实际位置相比较浅，也就是说反演误差随深度的增加而增大。在横向展布上，异常体的分布范围比隧道的实际宽度要大，横向分辨率较低。产生上述问题的主要原因是该方法的理论假设是水平层状介质，而本次试验场地在横向上存在剧烈变化(有空洞存在)，不满足水平层状介质假设，从而对频散曲线的反演精度造成一定的影响[21]。尽管如此，异常体的位置总体上与隧道的实际位置仍具有较好的对应关系，这说明利用粘弹介质勒夫波频散曲线反演浅层横波速度结构是可行且有效的，对于横向速度变化不大的地层，理论上应该能够获得更好的反演结果。

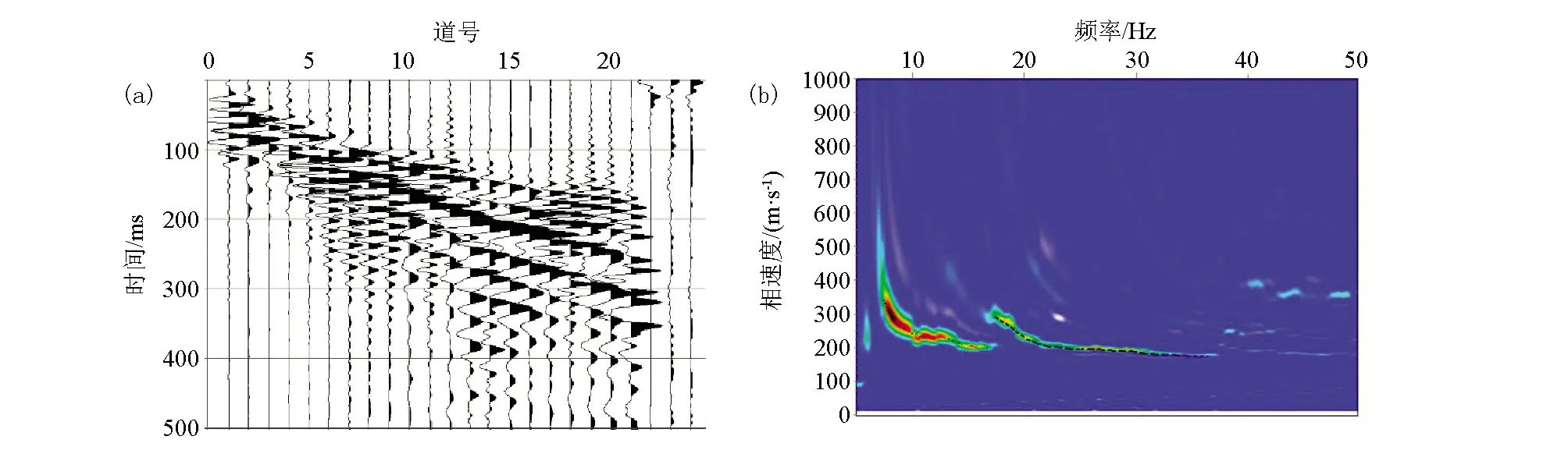
图9 第一炮野外勒夫波记录(a)及其频散曲线(b)Fig.9 The first shot of field Love-wave record(a) and its dispersion curves(b)

图10 野外实际资料频散曲线反演二维横波速度结构断面Fig.10 2-D shear wave velocity profile from the dispersion curve inversion of field data

4 结论

本文通过求解频散方程获得粘弹介质勒夫波理论相速度频散曲线，建立了一个有代表意义的三层速度递增模型，采用高阶有限差分方法模拟得到了勒夫波单炮记录。通过对理论模型提取得到频散曲线与理论频散曲线的对比研究以及实际资料处理，得到如下结论：

1)勒夫波频散曲线的高频极限趋近于最上层介质的横波速度，而低频极限趋近于最下层介质的横波速度，反演时可根据这一信息选择一个合适的初始模型。

2)勒夫波频散曲线的高阶模式以及各阶模式的高频成分对介质的粘弹性较为敏感。高阶模式的相速度随介质粘弹性的增强而增加。各模式频散曲线的最低相速度均高于完全弹性情况下的理论相速度，且随着频率的增高，介质粘弹性越强，各阶模式的高频极限收敛速度越大。

3 )理论模型及野外试验表明利用粘弹介质勒夫波频散曲线反演浅层横波速度结构是可行且有效的，反演时考虑介质的粘弹性可得到更为精确的反演结果。