冬小麦产量结构要素预报方法

张 佩，陈郑盟，刘春伟，王福政，江海东，高 苹

冬小麦产量结构要素预报方法

张 佩1，陈郑盟2，刘春伟3，王福政4，江海东5，高 苹1※

（1. 江苏省气象局，南京 210008；2. 福建省烟草公司龙岩市公司，龙岩 364000；3. 江苏省农业气象重点实验室、南京信息工程大学应用气象学院，南京 210044；4. 勤耕仁现代农业科技发展（淮安）有限责任公司，淮安 223001；5. 南京农业大学农业部作物生理生态与生产管理重点实验室、江苏省现代作物生产协同创新中心、国家信息农业工程技术中心，南京 210095）

为优选出最佳的冬小麦产量结构要素预报方法，该研究选择冬小麦成穗数、穗粒数及千粒质量为预报目标，综合考虑种植品种、密度及地区因子，并对气象因子进行膨化统计，得到126个自变量因子，分别采用多元线性回归、因子分析—线性回归及BP（Back Propagation）神经网络等3种方法进行建模分析。结果表明，直接采用各因子进行回归分析无法解决不同自变量间存在的多重共线性问题，而因子分析虽然消除了不同自变量间的多重共线性，但采用因子优化后的10个综合因子分别对3个产量结构要素进行线性回归，得到的预报模型决定系数（2）均不足0.500。运用BP神经网络对冬小麦3个产量结构要素进行预报，结果发现，当输入层为126、隐含层为16、输出层为3时，BP神经网络结构最佳，在此结构下，模型的决定系数为0.644，明显优于多元线性回归及因子分析-线性回归法。同时，基于BP神经网络模型对冬小麦产量结构要素的预报精度平均达85.3%。因此，推荐采用BP神经网络模型对冬小麦产量结构要素进行预报。

作物；冬小麦；产量结构要素；多元线性回归；因子分析；BP神经网络

0 引 言

作物产量预报可为政府制定粮食计划及农业生产决策提供依据，是当前气象为农服务的主要内容之一。中国作物产量预报研究始于20世纪70年代末，经过一系列项目研究和业务化试验研究，其预报理论及方法迅速发展[1-6]，并在20世纪90年代建成作物产量预报业务系统[7]投入业务应用。发展至今，最为成熟的作物产量预报模型仍以气象学统计方法为主，并普遍采用气象产量模型[8-9]。然而在气象产量数据的获取中，需要对产量数据进行平滑处理，这就在一定程度上消减了气象因子的波动性。气象因子的波动往往体现为阶段性，特别是农作物特定生育阶段的气候变化会导致某些产量构成要素的变化。王馥棠[10]20世纪80年代初即提出，准确预报产量结构要素不仅可以辅助预报最终产量，且可以揭示产量预报的生理学意义。

由于同一作物不同品种的自身生理特性及其对生长区域适应性的差异[11]，其生育期特征、根系形态[12-14]、水肥吸收特征[15-17]、光合特性[18-19]及对逆境的抵抗能力[20-21]均有不同程度的差异；不同的种植密度形成不同的群体结构及光能利用效率[22-24]，从而造成群体间的个体的生长发育存在差异[25]。这些差异都最终影响产量结构要素的水平。另外，同一作物在不同地区的种植品种、农艺措施也各不相同。因此，在进行产量结构要素预报时，需同时考虑品种、种植密度和地区因子。另外，以往的研究在气象因子的选择上，多数采用独立时间段（如月、旬或生育阶段）的气象因子进行预报[26-29]，而冬小麦的生长发育是一个连续的累积过程，这种时间尺度的不同选择也会影响产量的预测精度。汤志成等[4]在20世纪80年代中期即提出因子膨化处理的方法，并将其应用在早稻的产量预报上，很好地解决了这一问题。

在众多作物产量预报的统计方法中，多元回归法由于原理简单、使用便捷，被普遍使用[30-31]。因子分析法是一种有效的降维分析方法，它通过研究众多自变量间的内部依赖关系，从而把众多因子归结成少数几个包含原来众多变量信息的综合因子，可有效消除原有变量间的多重共线性，同时简化了数据结构。BP（Back Propagation）神经网络是众多人工神经网络（Artificial Neural Networks；ANN）中的一种，因其能学习和存储大量输入-输出模式的映射关系，而无需事前揭示描述这种映射关系的数学方程，可以逼近任意连续函数，具有很强的非线性映射能力，特别适合多因素对多因素关联预测模型的构建，目前已广泛应用于各个领域[32-36]。近年来，该方法也越来越多地被应用到农业气象预报上，如病虫害预测[37-38]、小气候预测[39]、产量预报[40-41]等。

本文选择冬小麦成穗数、穗粒数及千粒质量为预报目标，在膨化统计气象因子的基础上，综合考虑冬小麦种植品种、密度及地区因子，分别采用多元线性回归、因子分析—线性回归及BP神经网络进行预报模型的构建，通过预报结果与实测数据对比分析，得到最佳的预报模型，提高冬小麦产量预报效果，并为业务应用提供新的科学方法依据。

1 材料与方法

1.1 数据来源

冬小麦农业气象观测资料及气象观测资料源于江苏省气象信息中心。其中，江苏省冬小麦农业气象观测普遍始于20世纪80年代初，观测站点包括昆山、兴化、如皋、大丰、淮安、盱眙、滨海、徐州、沭阳及赣榆10个（见表1），预报产量结构要素主要包括株成穗数、穗粒数及千粒质量；气象观测资料为对应年份前一年10月至当年5月的逐日观测资料，气象因素主要包括逐日的平均气温（℃）、最低气温（℃）、降水量（mm/d）、日照时数（h）等。冬小麦种植品种、密度及地区从农业气象观测资料中查阅。

1.2 预报因子选择与处理

1.2.1 气象因子膨化

以逐月总积温T（℃）、累计降水量R（mm）及总日照时数S（h）作为表征冬小麦生长的主要热量、水分及光照条件，考虑秋冬春季低温往往对冬小麦生长造成较大影响，本文还统计了前一年11月至当年3月逐月日最低温度≤0 ℃的日数D（d）。

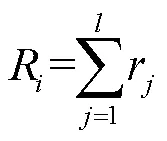
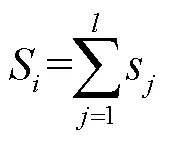
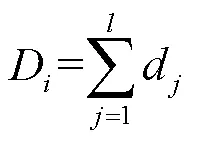
式中t为逐日平均气温，℃；r为逐日降水量，mm/d；s为逐日日照时数，h；minj为逐日最低气温，℃，为生育期内月份的序号数，取10，11，12，…，17（其中10表示前一年10月，13表示当年一月，依此类推）；为每个月份的日序，表示每个月总天数，d；d为日最低温度是否≤0 ℃的判断函数。

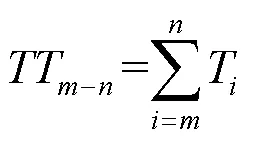
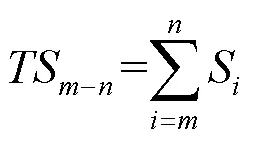
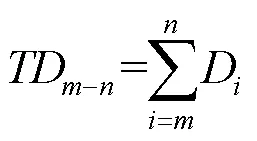
经过膨化处理，共得到总积温、累计降水量及总日照时数各36个序列，日最低温度≤0 ℃的日数15个序列，共123个不同时段的气象因子（表2）。

1.2.2 品种因子

通过品种审定公告获取所有供分析站点历史栽培品种的理论千粒质量，以此作为各冬小麦品种的表征因素。

1.2.3 地区因子

10个冬小麦农业气象观测站点分布相对均匀，站点的纬度跨度为31.4167° N～34.8333°N，经度跨度为117.1500°E～120.9500°E。本研究依据江苏农业区划，将10个站点分别归为6个地区，并给每个地区赋值[1，6]（表3）。

1.2.4 种植密度

种植密度是直接影响产量结构的重要因素之一，本文统计了各站点历年冬小麦的亩基本苗数（104株）作为种植密度的表征因子。

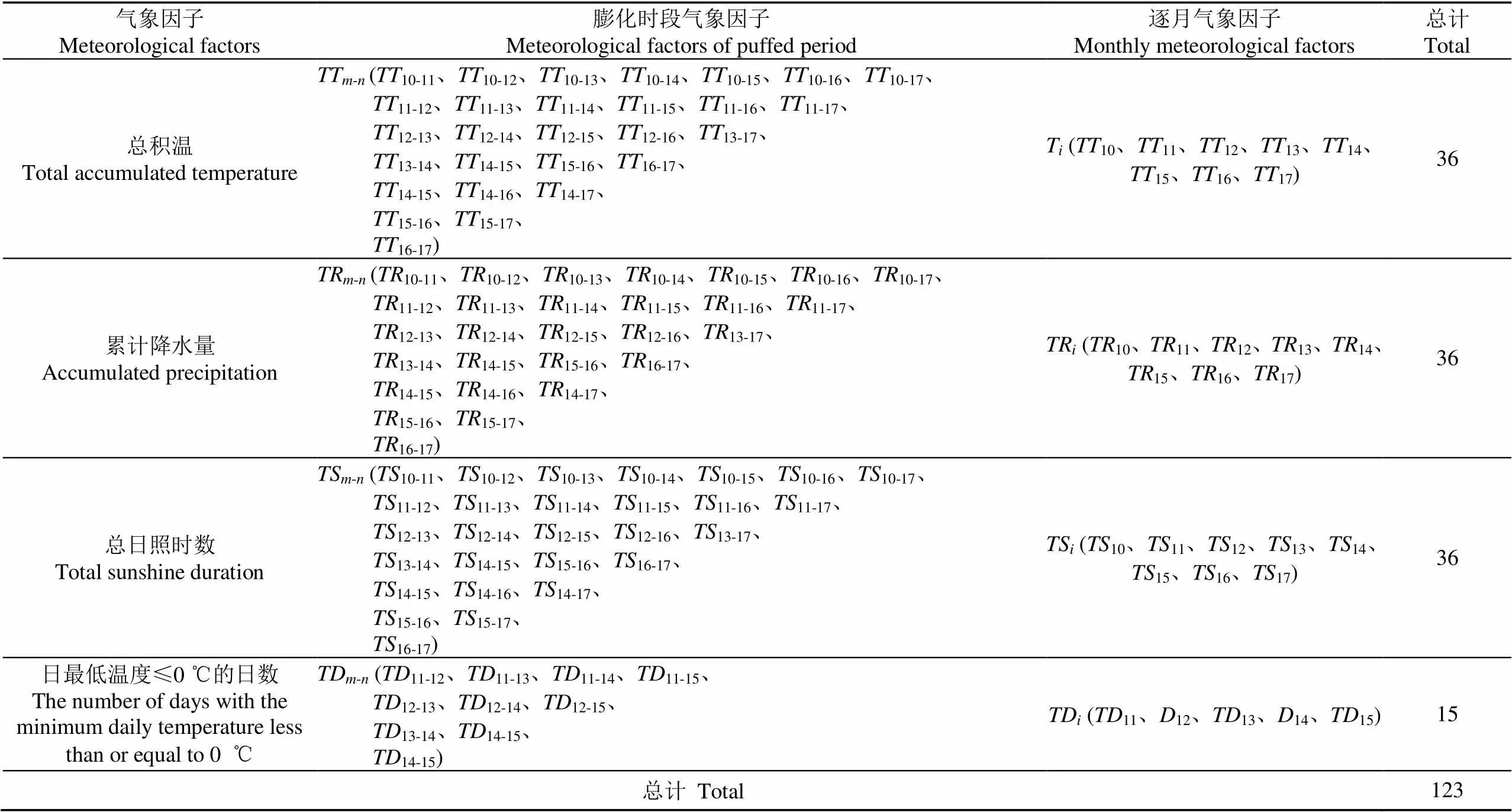
表2 不同时段的气象因子

注：下标-表示膨化组合时段的起止月份，为生育期内月份的序号数；下标10表示前一年10月，13表示当年一月，依此类推。

Note: The subscript-represents the starting and ending months of puffed period,is the ordinal number of the months during the growth period; which takes 10,11,12, ... , 17; The subscript 10 represents October of the previous year, 13 represents January of the current year, and so on.

表3 冬小麦农业气象观测站点分区及赋值

1.3 预测模型的构建方法

经过以上因子预处理，共得到气象、品种、地区及种植密度等4类共126个因子。由于已经考虑地区因子，并对其进行赋值处理，10个站点参与建模的样本（见表1）均可作为独立样本，本文将其融合形成一个样本数为274的建模序列，采用线性回归、因子分析-线性回归及BP神经网络法等3种方式建立3个产量结构要素的预报模型。然后分别从模型的拟合度、显著性及共线性检验等角度对预测模型的拟合效果进行判定，并计算80个验证样本的预报精度，用以评价模型的预报效果。

1.3.1 多元线性回归

多元线性回归是一种常用的预测建模方法，适用于以一个或多个自变量因子来解释某一因变量的计量分析。本研究利用SPSS软件，采用全相关方法首先对气象、品种、地区及密度等126个预报因子与株成穗数、穗粒数及千粒质量等3个冬小麦产量结构要素进行相关分析，然后基于最小二乘法（Ordinary Least Square，OLS），采用逐步回归法构建了冬小麦各产量结构要素预报的最优回归模型。

设Y为某一冬小麦产量结构要素，1,2,3, …,x分别代表用来说明Y的不同自变量因子，则所建立的冬小麦产量结构要素与各气象因子之间的线性关系模型为

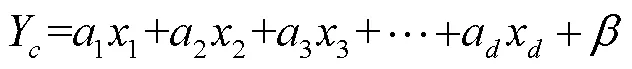
式中为随机变量，为常数项；1,2,3, …,a是各自变量因子1,2,3, …,x对应的回归系数，表示在其他因子不变的情况下，x增加或减少一个单位引起Y增减的平均值；为冬小麦产量结构要素序号，本文取1，2，3；为参与建模的自变量因子序号。

1.3.2 因子分析-线性回归

因子分析法可将众多变量转化成少数具有代表性的综合因子，这一方面可以解决因子间的共线性问题，同时也可简化数据结构。本研究自变量因子达126个，将因子降维分析变为可能。因此，尝试采用因子分析法进行因子优化。本文采用主成分分析法对梳理的变量进行因子分析。首先，对参与因子分析的变量进行Kaiser-Meyer-Olkin（KMO）检验与巴特利（Bartlett）球形检验，当KMO值＞0.7，Bartlett检验的值＜0.05，即说明变量可进行下一步的因子分析。然后根据因子特征值、累积贡献率表及碎石图，确定最佳综合因子，并输出转化后的综合因子，并以此作为线性回归的自变量，构建因子分析-线性回归模型，回归操作方法详见1.3.1。

1.3.3 BP神经网络

BP神经网络模型拓扑结构包括输入层（input）、隐层（hide layer）和输出层（output layer）。为能做有效对比，使用与回归模型相同的126个因子作为为输入层因子；输出层为株成穗数、穗粒数及千粒质量等3个冬小麦产量结构要素。

神经网络法的预测精度主要受制于隐含层节点数目；若节点数过少，将影响网络的学习效果，则需要增加训练次数，而这又会降低训练的精度；反之，网络训练时间增加，网络易过拟合。本文先由经验公式（10）确定不同的神经元数[42]，然后进行训练对比，以得到最佳的隐含层神经元个数。

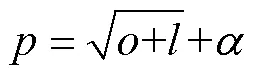
式中、、分别为隐含层、输入层及输出层的神经元数，为[1，10]之间的常数。

采用MATLAB 2016R软件的Neural Network Toolbox来构建冬小麦3个产量结构要素的BP网络神经预测模型，操作步骤如下：

1）数据的归一化处理。由于影响冬小麦产量结构要素的因子较多，且各因子原始数据的级差差异明显，本研究在进行BP神经网络构建前先对原始数据进行归一化处理，将数据线性压缩到[−1，1]的范围，使在训练阶段的网络更易收敛。

2）网络训练。网络中间层神经元传递函数采用Logsig函数，输出层神经元传递函数采用线性函数Purelin，训练函数采用Trainlm。将数据的75%用于模型训练，15%用于预测验证，10%用于模型测试。设置模型的收敛误差为0.000 1，学习速率为0.05，最大训练次数为1 000。

1.4 模型的预测精度

利用所构建的预测模型对各站点预测样本的冬小麦各产量结构要素进行预测精度PA的验证，公式如下

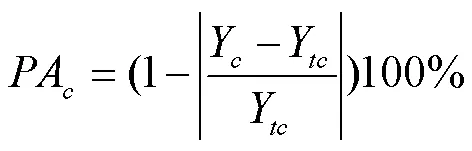
式中Y为小麦产量要素的实际值。

2 结果与分析

2.1 线性回归模型

采用逐步回归的方式对数据进行线性回归分析，并通过OLS法构建3个产量结构要素的预测模型（表4）。从表4中可见，3个产量结构要素的回归方程均通过了显著性检验（＜0.01）。其中，冬小麦成穗数回归模型的主要解释变量是基本苗数、地区因子及2—5月总积温；穗粒数回归模型的主要解释变量是地区因子、基本苗数、3月日照时数及2－4月总降水量；千粒质量回归模型主要由品种审定千粒质量、3－5月总日照时数、1－4月总积温、4－5月总降水量及基本苗数5个因子共同解释。

表4 冬小麦产量结构要素的多元线性回归预测模型结果

注：1为亩基本苗数，2为地区因子，3为2－5月总积温，4为3月日照时数，5为2－4月累计降水量，6为品种审定千粒质量，7为3－5月总日照时数，8为1－4月总积温，9为4－5月累计降水量。

Note:1isbasic seedlings per mu;2is region factor;3is total accumulated temperature from February to May;4is sunshine hours in March;5is accumulated precipitation from February to April;6is 1000-grain weight of audited variety;7is sunshine hours during March to May;8is total accumulated temperature from January to April;9is accumulated precipitation from April to May.

从表4可以看出，产量结构要素预报模型的决定系数2分别为0.515、0.178和0.368，共线性诊断发现直接回归分析时，多个维度特征值趋于0或对应条件指数大于10，这表明不同自变量间存在着多重共线性的问题（表5）。

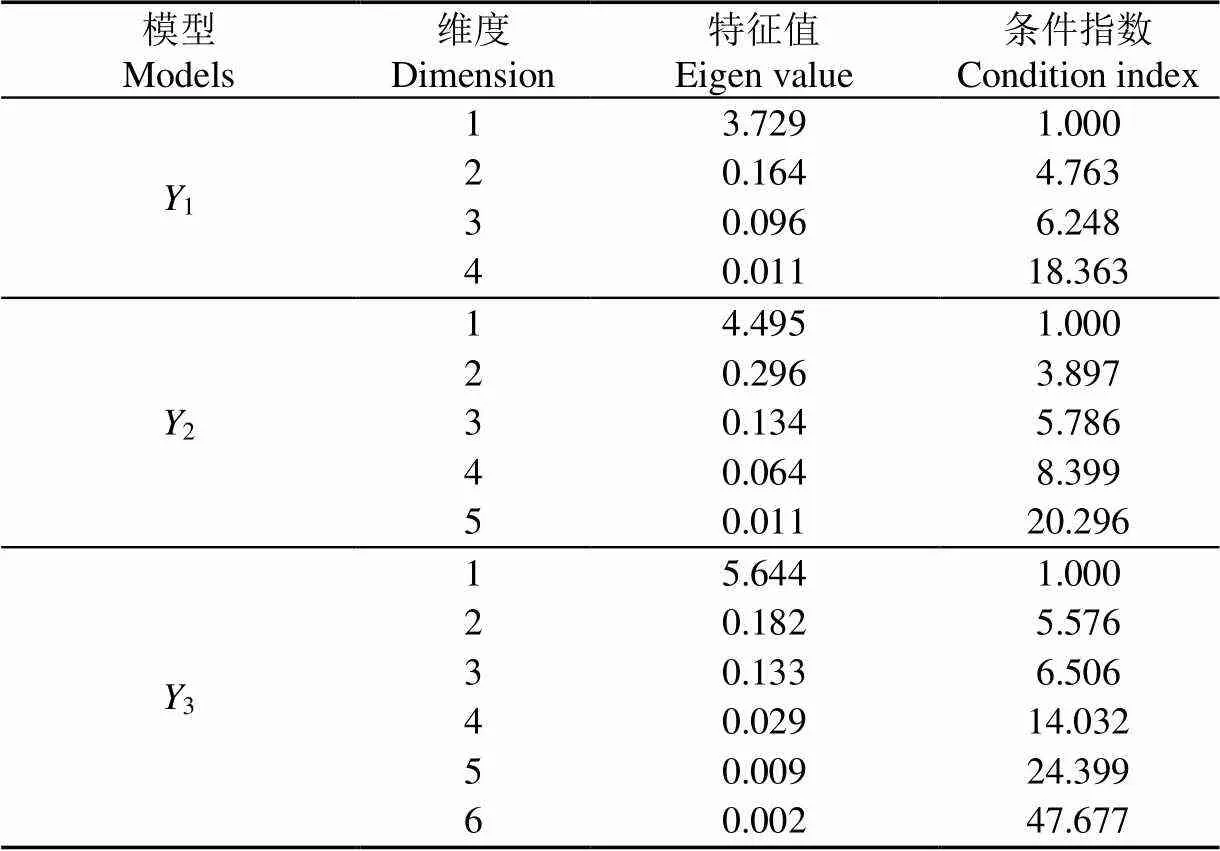
表5　冬小麦产量结构要素的多元回归预测模型共线性诊断结果

2.2 因子分析法

首先对126个因子进行因子分析，结果发现由于经过膨化处理的气象因子为非正定矩阵，无法进行球形检验，即无法进行因子分析。因此，剔除组合时段的气象因子，继续运用主成分分析法将余下32个因子进行因子分析，结果发现，KMO值为0.738，Bartlett检验的值接近0，这说明参与因子分析的数据顺利通过球形检查，并根据特征值大于1和累计贡献率确定10个综合因子（表6）。

通过SPSS将输出的10个综合因子分别对株成穗数、穗粒数及千粒质量进行回归，得到方程：

株成穗数：

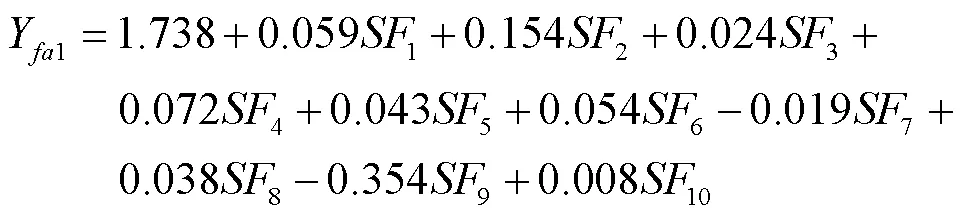
穗粒数：

千粒质量：

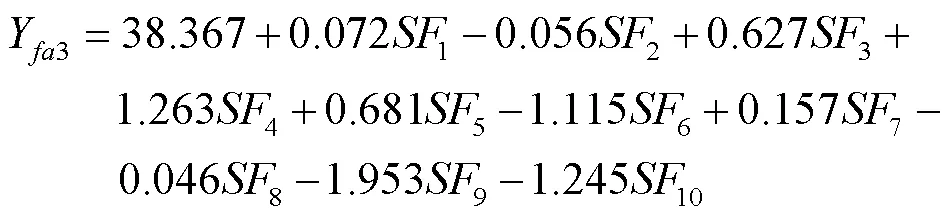
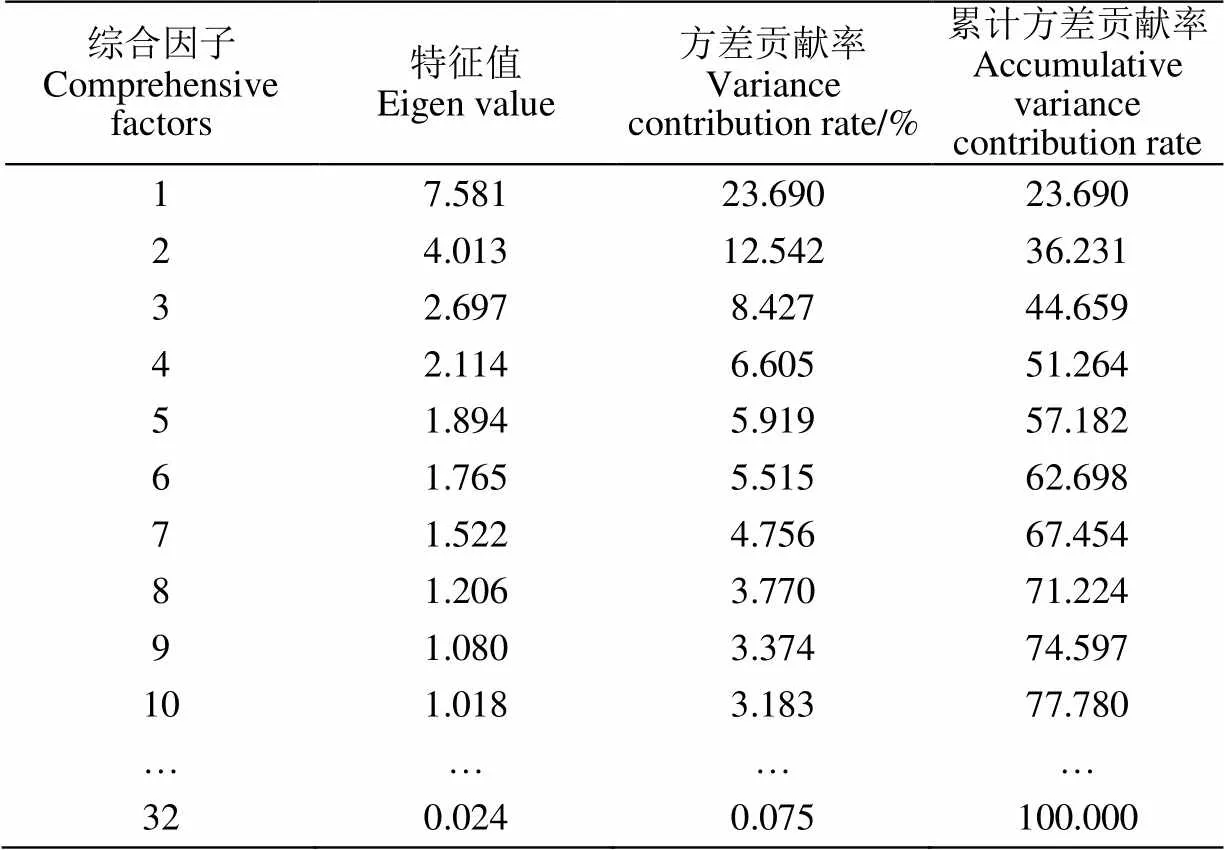
表6 综合因子的方差分析结果

表7 因子优化后的冬小麦产量结构要素预测模型结果

2.3 BP神经网络法

根据式（10），经过多次优选后，发现=126，=3，=5时，=16，此结构下BP网络收敛效果最佳，由此确定本研究最佳BP 神经网络结构为126-16-3。由图1可以看出，训练值和目标值的相关系数达0.803，决定系数为0.644，高于通过多元线性回归及因子分析-线性回归法构建的预测模型决定系数，这说明通过BP神经网络构建的模型模拟效果较好，明显优于多元回归及因子分析法。

图1 BP神经网络训练模型的拟合值与实际值的比较

2.4 基于BP神经网络模型的产量精度预测效果

利用6个地区10个站点2011－2018年产量结构资料对模型预测精度进行验证，结果见图2。可以得到，基于BP神经网络模型对江苏省冬小麦产量结构要素的预测精度平均达85.3%。分预报对象来看，BP神经网络模型对冬小麦穗粒数及千粒质量的预测精度明显高于株成穗数，穗粒数的预测精度平均为88.1%，其中苏南、东部沿海及沿淮沿海地区的预测精度均超90%，东部沿海最高达95.1%；千粒质量的预测精度平均为89.5%，其中苏南、东部沿海、沿淮沿海及淮北地区的预测精度全部超90.0%；而株成穗数的预测精度普遍较低，除沿淮（88.3%）及东部沿海（81.1%）外，其他地区均不足80%。

分地区来看，BP神经网络模型对6个地区冬小麦产量结构要素的平均预测精度由高到低依次为：东部沿海（89.6%）＞沿淮沿海（86.4%）＞沿淮（86.3%）＞苏南（84.3%）＞淮北（83.0%）＞江淮（81.3%）。从预测结果的标准误差来看，BP神经网络模型对6个地区的3个产量结构预测的标准误差普遍较低，说明其非线性的建模特征对处理多因子有着更强的能力，预测的稳定性较高。

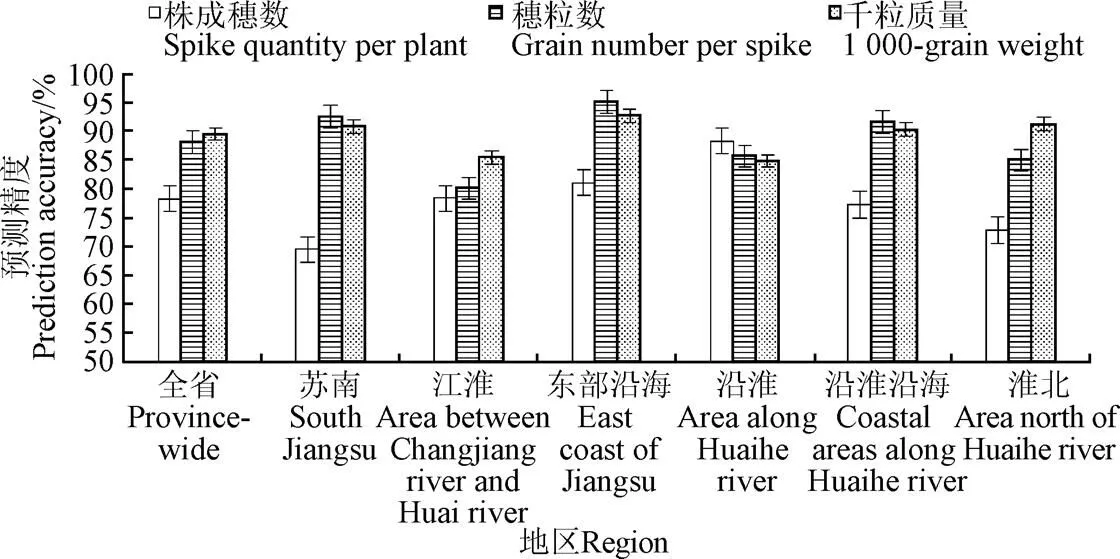
图2 BP神经网络模型对江苏冬小麦产量结构要素的预测精度

3 讨 论

作物产量结构要素的数据序列隐含了大量的动态特征，而且影响因素众多。预测产量需要选取的影响因素相互独立，这就使得影响因素的选择非常复杂且难度较大。

利用多元线性回归模型可以在众多因子中寻找与各产量结构要素关系密切的主要因素，以此为依据，可以对农业生产进行阶段性指导。从各因子和3个冬小麦产量结构要素的相关分析结果来看，株成穗数与基本苗数呈负相关关系（=−0.646**，**表示相关通过0.01水平显著性检验，下同），即基本苗数越多，表示冬小麦种植密度越大，对后期的成穗存在明显的限制；地区因子对株成穗数的影响主要体现在株成穗数的空间分布上（=0.316**），成穗数自南向北越来越多，这可能是由于小麦品种的冬性自南向北趋于明显，对应的成穗特征由少穗大穗向多穗小穗变化[43]；2－5月总积温越高，成穗数越多（=0.099），这可能是冬小麦返青后热量条件越好，群体营养生长旺盛，抑制成穗[43]。穗粒数回归模型中地区因子的表现也符合北方多穗小穗、南方少穗大穗的规律，与成穗数相反，穗粒数与地区因子呈负相关关系（=−0.330**），它呈现北少南多的分布趋势；穗粒数与亩基本苗数呈负相关关系（=−0.161**），当基本苗数越多，后期成穗受阻，穗数的降低一定程度上会促进穗型的成长，从而使穗粒数增加。而在千粒质量的回归模型中，品种特性是首要因子（=0.450**），3－5月总日照时数（=0.366**）及1－4月总积温（=0.049）越多，即光温条件越好，则越利于冬小麦籽粒的充实积累，而4－5月总降水量（=−0.283**）越多，可能是灌浆成熟阶段遇连续阴雨过程，使籽粒灌浆受阻，最终导致千粒质量下降；亩基本苗数与千粒质量呈负相关关系（=−0.288**），依据前述分析结果，基本苗数越多，促进穗型的成长而使穗粒数增加，这就限制了籽粒个体的生长。

但各自变量因子不是独立存在，它们往往相互影响、相互制约。本文直接对126个自变量因子进行线性回归建模后发现，3个冬小麦产量结构要素预报模型的决定系数2均较低，且不同自变量因子间存在着多重共线性的问题。而多重共线性会造成参数估计量含义不合理，变量的显著性检验失去意义，可能将重要的解释变量排除在模型之外，进而导致模型的预测功能失效。另外，由于多元线性回归模型摒弃了其他因子，仅把与产量结构要素相关性大的主要因子作为预报因子进行建模，如果当被摒弃的因子发生异常时，多元回归模型就会放大该因子的波动性，其预测结果就会产生较大误差。李蓬勃等[44]研究也发现，利用多元回归法构建粮食产量的预测模型时，会出现数据信息的屏蔽效应，而导致模型预测精度不高。因此可以看出，多元回归模型是一种线性估计算法，在对复杂过程特别在对多种不同类别因子的模拟上存在明显的局限性。尤其是当建模因子较多时，多元回归法无法解决各自变量因子间可能存在的多重共线性问题。

解决多重共线性的主要方法有3类，一是排除引起共线性的变量，如逐步回归法；二是差分法，将原模型变换为差分模型；三是减小参数估计量的方差，如岭回归法。在本研究中，已经采取了逐步回归法，但是模型仍存在多重共线性；而采用差分模型、岭回归模型由于因变量数量过大，会降低模型的鲁棒性，过多冗余信息会导致数据处理时间过长。因子分析法是一种有效的降维分析方法，不仅可以解决原来因子间的共线性问题，同时也可简化数据结构。本文采用因子分析法确实消除了不同自变量间的多重共线性，但采用因子优化后的10个综合因子分别对3个产量结构要素进行线性回归，得到的预测模型的拟合效果仍然欠佳。

BP神经网络模型对输入-输出因子没有限制，能够以较高精度逼近任何线性或非线性连续函数，特别适合多因素对多因素关联预测模型的构建。在前人的研究[40-41]中，大部分基于BP神经网络的产量预测普遍只针对单产一个因素，即为非线性多对一映射。本文的建模因子达126个，预测目标为3个，建模样本为274个，采用BP神经网络，也能快速有效地得到了最佳网络结构（126-16-3），所构建的模型对冬小麦产量结构要素的预测精度平均达85.3%，且预测的稳定性较高。但BP神经网络自身也存在缺点，由于其没有对主导预测因子进行筛选的功能[45]，多为纯方法论研究，对模型的生理学意义较少关注。本文在建模前，充分考虑了冬小麦各产量结构要素可能的影响因子，最终将种植品种、密度及地区也作为预报因子，在一定程度上弥补了BP神经网络缺少生理解释的不足。

4 结 论

作物最终产量的变化是由各产量结构要素的变化引起的，因此，本文以冬小麦成穗数、穗粒数及千粒质量为研究目标，在对气象因子进行膨化处理的基础上，综合考虑种植品种、密度及地区因子，分别采用多元线性回归、因子分析-线性回归及BPNN神经网络等3种方法进行建模分析。结果如下：

1）利用多元线性回归法构建冬小麦产量结果要素的预测模型时，可以在众多因子中寻找与各产量结构要素关系密切的主要因素，但对模型进行共线性诊断发现，多个维度特征值趋于0或对应条件指数大于10，即参与模型构建的自变量间存在多重共线性。

2）采用因子分析法可消除不同自变量间的多重共线性，但采用因子优化后的10个综合因子进行模型构建，3个产量结构要素预测模型的决定系数2均小于0.5，拟合效果欠佳。

3）基于BP神经网络进行冬小麦产量结构要素预测模型的构建时得到，最佳BP 神经网络结构输入层为126、隐含层为16、输出层为3，模型的决定系数2为0.644，均高于多元线性回归及因子分析—线性回归法构建的预测模型，且模型对各产量结构要素的预测精度平均达85.3%，其中对穗实粒数及千粒质量的预测精度接近90%。这说明基于BP神经网络法构建的冬小麦产量结构要素预测模型的预测效果较好，可辅助预报冬小麦最终产量。

仍有一些问题有待进一步研究，如模型对株成穗数的预测精度仍偏低，且对江淮地区冬小麦各产量结构要素的预测精度较其它地区也偏低。因此，如何提升预测模型对不同预报对象、不同地区的预测效果将是下一步的研究重点之一。

[1] 吴元中. 产量预报中资料处理方法的探讨[J]. 中国农业气象，1982，2：61-64.

Wu Yuanzhong. Discussion on data processing method in yield forecast[J]. Chinese Journal of Agrometeorology, 1982, 2: 61-64. (in Chinese with English abstract)

[2] 宛公展，王宝成，蓝鸿第. 华北地区冬小麦产量预报模式的初步研究[J]. 气象学报，1984，42(3)：356-363.

Wan Gongzhan, Wang Baocheng, Lan Hongdi. A preliminary study of yield forecast model for winter wheat in North China[J]. Acta Meteorologica Sinica, 1984, 42(3): 356-363. (in Chinese with English abstract)

[3] 周电辉. 模糊数学在研究定西地区胡麻产量预报中的应用[J]. 植物生态学与地植物学丛刊，1985，9(2)：120-131.

Zhou Dianhui. Application of fuzzy mathematics in study of common flax yield forecasting in Dingxi area[J]. Acta Phytoecologica Et Geobotanica Sinica, 1985, 9(2): 120-131. (in Chinese with English abstract)

[4] 汤志成，邹永林. 江苏省双季早稻产量预报的累加型模式[J]. 江苏农业学报，1986，2(3)：12-19.

Tang Zhicheng, Zou Yonglin. Regional rice yield prediction from weather data: A successive regression model[J]. Journal of Agricultural Sciences, 1986, 2(3): 12-19. (in Chinese with English abstract)

[5] 王春乙，潘亚茹. 用带周期分量的逐步回归模型预测冬小麦产量的试验[J]. 气象，1989，15(8)：22-25.

Wang Chunyi, Pan Yaru. An approach to winter wheat yield prediction using a model with orthogonal factors and periodic components[J]. Meteorological Monthly, 1989, 15(8): 22-25. (in Chinese with English abstract)

[6] 汤志成，孙涵. 产量预报的加权多重回归模型[J]. 中国农业气象，1992，13(4)：24-28.

Tang Zhicheng, Sun Han. The model of weighted multiple regression for yield prediction. Chinese Journal of Agrometeorology, 1992, 13(4): 24-28. (in Chinese with English abstract)

[7] 庄立伟，王馥棠，王石立. 农业气象产量预测业务系统的研制[J]. 应用气象学报，1996，7(3)：294-299.

Zhuang Liwei, Wang Futang, Wang Shili. Development of agrometeorological yield forecasting operational system[J]. Quarterly Journal of Applied Meteorology, 1996, 7(3): 294-299. (in Chinese with English abstract)

[8] 王培娟，张佳华，谢东辉，等. A2和B2情景下冀鲁豫冬小麦气象产量估算[J]. 应用气象学报，2011，22(5)：549-557.

Wang Peijuan, Zhang Jiahua, Xie Donghui, et al. Estimation for weather yield of winter wheat under A2 and B2 scenarios in Hebei, Shandong and Henan Provinces[J]. Journal of Applied Meteorological Science, 2011, 22(5): 549-557. (in Chinese with English abstract)

[9] 王媛，方修琦，徐锬，等. 气候变化背景下“气候产量”计算方法的探讨[J]. 自然资源学报，2004，19(4)：531-536.

Wang Yuan, Fang Xiuqi, Xu Tan, et al. A method for calculating the climatic yield of grain under climate change[J]. Journal of Natural Resources, 2004, 19(4): 531-536. (in Chinese with English abstract)

[10] 王馥棠. 农业气象作物产量预报概述[J]. 气象科技，1983，2：36-41.

Wang Futang. An overview of agrometeorological crop yield forecast[J]. Meteorological Science and Technology, 1983, 2: 36-41. (in Chinese with English abstract)

[11] Liu Nian, Meng Daqing, Tang Tianze, et al. Ecological adaptability of new hybrid rapeseed varieties in Sichuan Hilly areas[J]. Agricultural Science & Technology, 2016, 17(1): 69-71.

[12] 刘俊萍，刘刚，游璐，等. 不同品种油茶细根时空分布动态[J]. 应用生态学报，2018，29(12)：3927-3933.

Liu Junpin, Liu Gang, You Lu , et al. Temporal and spatial distributions of fine roots of different varieties of Camellia oleifera[J]. Chinese Journal of Applied Ecology, 2018, 29(12): 3927-3933. (in Chinese with English abstract)

[13] 张耗，黄钻华，王静超. 江苏中籼水稻品种演进过程中根系形态生理性状的变化及其与产量的关系[J]. 作物学报，2011，37(6)：1020-1030.

Zhang Hao, Huang Zuanhua, Wang Jingchao. Changes in morphological and physiological traits of roots and their relationships with grain yield during the evolution of mid-season Indica Rice cultivars in Jiangsu Province[J]. Acta Agronomica Sinica, 2011, 37(6): 1020-1030. (in Chinese with English abstract)

[14] 田中伟，樊永惠，殷美，等. 长江中下游小麦品种根系改良特征及其与产量的关系[J]. 作物学报，2015，41(4)：613-622.

Tian Zhongwei, Fan Yonghui, Yin Mei, et al. Genetic improvement of root growth and its relationship with grain yield of wheat cultivars in the middle-lower Yangtze River[J]. Acta Agronomica Sinica, 2015, 41(4): 613-622. (in Chinese with English abstract)

[15] 闫学梅，于振文，张永丽，等. 不同小麦品种耗水特性和籽粒产量的差异[J]. 应用生态学报，2011，22(3)：694-700.

Yan Xuemei, Yu Zhenwen, Zhang Yongli, et al. Differences in water consumption characteristics and grain yield of different wheat cultivars[J]. Chinese Journal of Applied Ecology, 2011, 22(3): 694-700. (in Chinese with English abstract)

[16] 黄芳，韩晓宇，王峥，等. 不同年代冬小麦品种的产量和磷生理效率对土壤肥力水平的响应[J]. 植物营养与肥料学报，2016，22(5)：1222-1231.

Huang Fang, Han Xiaoyu, Wang Zheng, et al. Responses of grain yield and phosphorus physiological efficiency of wheat cultivars released in different decades to soil fertility levels[J]. Journal of Plant Nutrition and Fertilizer 2016, 22(5): 1222-1231. (in Chinese with English abstract)

[17] 董宝娣，张正斌，刘孟雨，等. 小麦不同品种的水分利用特性及对灌溉制度的响应[J]. 农业工程学报，2007，23(9)：27-33.

Dong Baodi, Zhang Zhengbin, Liu Mengyu, et al. Water use characteristics of different wheat varieties and their responses to different irrigation scheduling[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2007, 23(9): 27-33. (in Chinese with English abstract)

[18] 敖雪，谢甫绨，刘婧琦，等. 同磷效率大豆品种光合特性的比较[J]. 作物学报，2009，35(3)：522-529.

Ao Xue, Xie Futi, Liu Jingqi, et al. Comparison of photosynthetic characteristics in soybean cultivars with different phosphorus efficiencies[J]. Acta Agronomica Sinica, 2009, 35(3): 522−529. (in Chinese with English abstract)

[19] 董志新，韩清芳，贾志宽，等. 不同苜蓿（L.）品种光合速率对光和CO2浓度的响应特征[J]. 生态学报，2007，27(6)：2272-2278.

Dong Zhixin, Han Qingfang, Jia Zhikuan, et al. Photosynthesis rate in response to light intensity and CO2concentration in different alfalfa varieties[J]. Acta Ecologica Sinica, 2007, 27(6): 2272-2278. (in Chinese with English abstract)

[20] 周玲，王朝辉，李富翠，等. 不同产量水平旱地冬小麦品种干物质累积和转移的差异分析[J]. 生态学报，2012，32(13)：4123-4131.

Zhou Ling, Wang Zhaohui, Li Fucui, et al. Analysis of dry matter accumulation and translocation for winter wheat cultivars with different yields on dryland[J].Acta Ecologica Sinica, 2012, 32(13): 4123-4131. (in Chinese with English abstract)

[21] 段骅，唐琪，剧成欣，等. 抽穗灌浆早期高温与干旱对不同水稻品种产量和品质的影响[J]. 中国农业科学，2012，45(22)：4561-4573.

Duan Hua, Tang Qi, Ju Chengxin, et al. Effect of high temperature and drought on grain yield and quality of different rice varieties during heading and early grain filling periods[J]. Scientia Agricultura Sinica, 2012, 45(22): 4561-4573. (in Chinese with English abstract)

[22] Leach J E, Stevenson H J, Rainbow A J, et al. Effects of high plant populations on the growth and yield of winter oilseed rape (L.)[J]. The Journal of Agricultural Science, 1999, 132 (2): 173-180.

[23] Momoh E J, Zhou W. Growth and yield responses to plant density and stage of transplanting in winter oilseed rape (L.)[J]. Journal of Aronomy and Crop Science, 2001, 186(4): 253-259.

[24] 徐宗贵，孙磊，王浩，等. 种植密度对旱地不同株型春玉米品种光合特性与产量的影响[J]. 中国农业科学，2017，50(13)：2463-2475.

Xu Zonggui, Sun Lei, Wang Hao, et al. Effects of different planting densities on photosynthetic characteristics and yield of different variety types of spring maize on dry land[J]. Scientia Agricultura Sinica, 2017, 50(13): 2463-2475. (in Chinese with English abstract)

[25] 邬小春. 密度对不同株型夏玉米单株生产力与群体产量的影响[D]. 杨凌：西北农林科技大学，2016.

Wu Xiaochun. Effects on Density on Individual Productivity and Yield of Different Plant Types Corn[D]. Yangling: Northwest A&F University, 2016. (in Chinese with English abstract)

[26] 吴普特，赵西宁. 气候变化对中国农业用水和粮食生产的影响[J]. 农业工程学报，2010，26(2)：1-6.

Wu Pute, Zhao Xining. Impact of climate change on agricultural water use and grain production in China[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2010, 26(2): 1-6. (in Chinese with English abstract)

[27] 高永刚，顾红，姬菊枝，等. 近43年来黑龙江气候变化对农作物产量影响的模拟研究[J]. 应用气象学报，2007，18(4)：532-538.

Gao Yonggang, Gu Hong, Ji Juzhi, et al. Simulation study of climate change impact on crop yield in Heilongjiang Province from 1961 to 2003[J]. Journal of Applied Meteorology, 2007, 18(4): 532-538. (in Chinese with English abstract)

[28] 蔺涛，谢云，刘刚，等. 黑龙江省气候变化对粮食生产的影响[J]. 自然资源学报，2008，23(2)：307-318.

Lin Tao, Xie Yun, Liu Gang, et al. Impact of climate change on crop yields in Heilongjiang Province[J]. Journal of Natural Resources, 2008, 23(2): 307-318. (in Chinese with English abstract)

[29] 孙卫国，程炳岩，杨沈斌，等. 区域气候变化对华东地区水稻产量的影响[J]. 中国农业气象，2011，32(2)：227-234.

Sun Weiguo, Cheng Bingyan, Yang Shenbin, et al. Impact of the regional climate variations on rice yield in East China[J]. Chinese Journal of Agrometeorology, 2011, 32(2): 227-234. (in Chinese with English abstract)

[30] 钱锦霞，郭建平. 郑州地区冬小麦产量构成要素的回归模型[J]. 应用气象学报，2012，23(4)：500-504.

Qian Jinxia, Guo Jianping. Regression models of winter wheat yield components in Zhengzhou area[J]. Journal of Applied Meteorological Science, 2012, 23(4): 500-504. (in Chinese with English abstract)

[31] 易雪，王建林，宋迎波. 气候适宜指数在早稻产量动态预报上的应用[J]. 气象，2010，36(6)：85-89.

Yi Xue, Wang Jianlin, Song Yingbo. Application of climatic suitability index to dynamical prediction of early rice yield[J]. Meteorological Monthly, 2010, 36(6): 85-89. (in Chinese with English abstract)

[32] Timothy R Green, Jose D Salas, Ana Martinez, et al. Relating crop yield to topographic attributes using Spatial Analysis Neural Networks and regression [J]. Science Direct, 2006, 139 (1): 23-37.

[33] 邵月红，张万昌，刘永和，等. BP神经网络在多普勒雷达降水量的估测中的应用[J]. 高原气象，2009，28(4)：846-853.

Shao Yuehong, Zhang Wanchang, Liu Yonghe, et al. Application of back-propagation neural network in precipitation estimation with Doppler Radar [J]. Plateau Meteorology, 2009, 28(4): 846-853. (in Chinese with English abstract)

[34] 瞿英，王冕，董文旭，等. 基于BP 神经网络的农田大气氨浓度预测[J]. 中国生态农业学报(中英文)，2019，27(4)：519-528.

Qu Ying, Wang Mian, Dong Wenxu, et al. Prediction of atmospheric ammonia concentration in farmlands using BP neural network[J]. Chinese Journal of Eco-Agriculture, 2019, 27(4): 519-528. (in Chinese with English abstract)

[35] 张漫，李婷，季宇寒，等. 基于BP 神经网络算法的温室番茄CO2增施策略优化[J]. 农业机械学报，2015，46(8)：239-245.

Zhang Man, Li Ting, Ji Yuhan, et al. Optimization of CO2enrichment strategy based on BPNN for tomato plants in greenhouse[J]. Transactions of the Chinese Society for Agricultural Machinery, 2015, 46(8): 239-245. (in Chinese with English abstract)

[36] 刘雪，李亚妹，刘娇，等. 基于BP 神经网络的鲜鸡蛋货架期预测模型[J]. 农业机械学报，2015，46(10)：328-334.

Liu Xue, Li Yamei, Liu Jiao, et al. BP neural network based prediction model for fresh egg’s shelf life[J]. Transactions of the Chinese Society for Agricultural Machinery, 2015, 46(10): 328-334. (in Chinese with English abstract)

[37] 刘庭洋，李烨，浦仕磊，等. 基于BP神经网络的稻瘟病预测预报研究[J]. 西南农业学报，2017，30(7)：1546-1553.

Liu Tingyang, Li Ye, Pu Shilei, et al. Investigation of rice blast prediction and forecast based on BP neural network[J]. Southwest China Journal of Agricultural Sciences, 2017, 30(7): 1546-1553. (in Chinese with English abstract)

[38] 靳然，李生才. 基于小波神经网络和BP 神经网络的麦蚜发生期预测对比[J]. 植物保护学报，2016，43(3)：353-361.

Jin Ran, Li Shengcai. Comparison of occurrence periods of wheat aphids based on artificial neural network and wavelet neural network prediction systems[J]. Journal of Plant Protection, 2016, 43(3): 353-361. (in Chinese with English abstract)

[39] 温永菁，李春，薛庆禹，等. 基于逐步回归与BP神经网络的日光温室温湿度预测模型对比分析[J]. 中国农学通报，2018，34(16)：115-125.

Wen Yongjing, Li Chun, Xue Qingyu, et al. Temperature and humidity prediction models in solar greenhouse: Comparative analysis based on stepwise regression and BP neural network[J]. Chinese Agricultural Science Bulletin, 2018, 34(16): 115-125. (in Chinese with English abstract)

[40] 戎陆庆，陈飞，欧阳浩. 基于GRA&BPNN的广西粮食产量预测研究[J]. 中国农业资源与区划，2017，38(2)：105-111.

Rong Luqing, Chen Fei, Ouyang Hao. Predicting grain yield of Guangxi province based on GRA＆BPNN[J]. Chinese Journal of Agricultural Resources and Regional Planning, 2017, 38(2): 105-111. (in Chinese with English abstract)

[41] 庄星，韩飞. 基于混合群智能算法优化BP 神经网络的粮食产量预测[J]. 江苏大学学报：自然科学版，2019，40(2)：209-215.

Zhuang Xing, Han Fei. Prediction of grain yield based on BP neural network optimized by hybrid swarm intelligence algorithm[J]. Journal of Jiangsu University：Natural Science Editon, 2019, 40(2): 209-215. (in Chinese with English abstract)

[42] 陶海龙. 基于混合智能算法的铁路运量预测研究[D]. 兰州：兰州交通大学，2012.

Tao Hailong. Study on Forecast of Railway Traffic Volume Based on Hybrid Intelligent Algorithm[D]. Lanzhou: Lanzhou Jiaotong University, 2012. (in Chinese with English abstract)

[43] 杨文钰，屠乃美. 作物栽培学各论[M]. 北京：中国农业出版社，2006.

[44] 李蓬勃，闫晓冉，徐东瑞. BP神经网络和多元线性回归在粮食产量空间分布预测中的比较[J]. 干旱区资源与环境，2014，28(9)：74-79.

Li Pengbo, Yan Xiaoran, Xu Dongrui. Comparison of grain yield spatial distribution forecast between the models of BP neural network and multiple linear regression[J]. Journal of Arid Land Resources and Environment, 2014, 28(9): 74-79. ( in Chinese with English abstract)

[45] 苏博，刘鲁，杨方廷. GM(1，N)灰色系统与BP神经网络方法的粮食产量预测比较研究[J]. 中国农业大学学报，2006，11(4)：99-104.

Su Bo, Liu Lu, Yang Fangting. Comparison and research of grain production forecasting with methods of GM(1 ,N)gray system and BPNN[J]. Journal of China Agricultural University, 2006, 11(4): 99-104. ( in Chinese with English abstract)

Method for the prediction of wheat yield components

Zhang Pei1, Chen Zhengmeng2, Liu Chunwei3, Wang Fuzheng4, Jiang Haidong5, Gao Ping1※

(1.210008,; 2.,364000,; 3.,,,210044,; 4.().,.,’223001,; 5.,,,,,210095,)

Accurate determination of yield components can assist in predicting the final crop yields, revealing the physiological significance of yield estimation. Research on the direct prediction of crop yield components is still lacking, because the feature data of yield components for long sequence are difficult to obtain, and some highly variable factors influence each other on the accuracy of the estimation. In this study, the spike quantity per plant (SQ), grain number per spike (GN), and 1000-grain weight (1 000 GW) of winter wheat were taken as prediction targets, to determine the optimal method for the prediction of winter wheat yield components. 126 independent factors were achieved using the puffing technology for meteorological factors after assessing the factors of planting species, density and region. A multivariable linear regression was used to analyze the crucial factors correlated to the concerned crop yield, and thereby to determine the quantitative relationship between the factors and yields. Three multiple regression models for the yield components of winter wheats were constructed after the 126 independent factors were regressed step by step. The determination coefficient2of the three multiple regression models were 0.515, 0.178 and 0.368, respectively,all at a low level than before. In collinearity diagnosis, if the characteristic values of multiple dimensions in 3 models were approaching to be zero, or the corresponding condition indexes were greater than 10, the time-delay prediction can occur due to the multicollinearity relation between factors. To solve this collinearity among factors and verify the data structure, a factor analysis was conducted to transform various observed variables into a few typical comprehensive factors. The optimized 126 independent variables made it possible to reduce the factor dimension. After factors optimization, 10 comprehensive factors were obtained to establish the three multiple regression predicting models of yield components, and the determination coefficient2were 0.376, 0.111 and 0.261, respectively, all less than 0.5. Based on neural network principle, a back-propagating neural network (BPNN) model was established between multiple independent factors and dependent variables, due to its ability for an approximate representation without restricting the input-output data. The determination coefficient2of the proposed model was 0.644 under the optimal model structure (126-16-3), indicating much better than that from the multiple linear regression and factor analysis. The overall prediction accuracy of BPNN model was 85.3%. The average prediction accuracies of grain number (GN) and 1000-grain weight (1 000 GW) were 88.1% and 89.5%, respectively, showing significantly higher than that of spike quantity per plant (SQ).In the prediction regions, the average prediction accuracies of the BPNN model were more than 80% in 6 regions, with the highest prediction accuracy of 89.6% in the east coast of Jiangsu.The results demonstrate that the nonlinear feature of BPNN model can be used to improve the approximation ability when dealing with multiple factors. The BPNN modeling is strongly recommended to predict yield components of winter wheat.

crops;winter wheat; yield components; multiple liner regression; factor analysis; BPNN

张佩，陈郑盟，刘春伟，等. 冬小麦产量结构要素预报方法[J]. 农业工程学报，2020，36(8)：78-87.doi：10.11975/j.issn.1002-6819.2020.08.000 http://www.tcsae.org

Zhang Pei, Chen Zhengmeng, Liu Chunwei, et al. Method for the prediction of wheat yield components[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2020, 36(8): 78-87. (in Chinese with English abstract) doi：10.11975/j.issn.1002-6819.2020.08.000 http://www.tcsae.org

2019-12-12

2020-02-29

国家重点研发计划课题（2018YFD1000900）；2019年国内外作物产量气象预报专项；江苏省“333工程”高层次人才培养科研项目；江苏省气象局科技项目（KM201905）

张佩，副高，主要从事应用气象及设施农业的研究。Email：78073954@qq.com

高苹，正研，主要从事应用气象研究。Email：571086340@qq.com

10.11975/j.issn.1002-6819.2020.08.010

S165+.27

A

1002-6819(2020)-08-0078-10