压差式管道机器人柔性多体系统流固耦合模型构建

滕晓艳，江旭东，马 睿

压差式管道机器人柔性多体系统流固耦合模型构建

滕晓艳1，江旭东2※，马 睿1

（1. 哈尔滨工程大学机电工程学院，哈尔滨 150001；2. 哈尔滨理工大学机械动力工程学院，哈尔滨 150080）

流体驱动下压差式管道机器人的运动属于复杂的流固耦合动力学问题，通过数值模拟方法分析机器人的动力响应，评估机器人在管道内的巡线能力具有重要的工程意义。该文基于耦合的欧拉-拉格朗日（Coupled Eulerian-Lagrangian，CEL）方法，构建了机器人柔性多体系统的流固耦合动力学模型，以平均驱动压差、平均摩擦力和密封皮碗的米塞斯应力峰值为指标，评价机器人对管道环境的适应性。数值模拟结果表明，与3舱段管道机器人相比，5舱段管道机器人的平均速度和速度波动幅值分别降低5.3%和18.6%，但是平均驱动压差、摩擦力和峰值米塞斯应力分别增加了56.9%、95.7%和42.0%。由此，随着舱段数增加，密封皮碗的变形进一步增加，流体需提供更大的驱动压差克服摩擦力作用，但机器人系统的速度平稳性有所提高。3舱段和5舱段机器人在管道焊瘤高度20 mm、弯道角度90°、弯道曲率半径300 mm时的平均摩擦力、平均驱动压差以及密封皮碗的米塞斯应力峰值均达到最大值：3舱段机器人分别为0.98 MPa、10.61 kN和28.30 MPa，5舱段机器人分别为0.63 MPa、5.64 kN和24.16 MPa。因此，与3舱段机器人相比，在弯道与焊瘤约束的联合作用下，5舱段机器人需要消耗更多的流体压力能克服管道的约束阻力；更高的摩擦力将使密封皮碗磨损加速，削弱密封性能，而更高的米塞斯应力峰值也将增加密封皮碗的脆性断裂风险，导致5舱段机器人对于管道环境的适应性弱于3舱段机器人。研究结果可为管道机器人的巡线能力评价和设计优化提供参考。

机器人；数值分析；流固耦合；柔性多体系统；压差式管道机器人；动力特性

0 引 言

管道运输广泛应用于工业、农业、民生领域中。由于管道的掩埋性，管道的高效维护（清理、焊接、防腐与检测等）主要由智能移动载体—管道机器人完成。压差式管道机器人系统通过两端流体压差的作用，将管道内流体压力能转变为动能，实现长距离管道的巡线与维护[1-3]。压差式管道机器人在作业过程中，运行速度平稳性、弯管通过性和越障能力等直接关系到作业效果的好坏[4-6]。因此，建立压差式管道机器人多体系统的计算模型，描述管道机器人在管内的运行状态和动力特性对于机器人的运动控制具有重要的理论与工程意义。

压差式管道机器人在管内运动时，驱动舱段和作业舱段在发生刚体运动的同时，也伴随密封皮碗的超弹性变形、舱段与流体的相互作用以及舱段的振动，属于典型的柔性多体动力学问题。Lesani等[7-8]构建了压差式管道机器人驱动舱段的三维刚体动力学模型，研究了驱动舱段在弯管中的运动轨迹和速度响应。Liang等[9]研制了含有制动单元的压差式管道机器人系统，构建了机器人系统制动过程的分析力学模型，研究了机器人系统的制动性能。Zhang等[10-12]采用柔性多体动力学方法，将密封皮碗简化为悬臂梁模型，分析了密封皮碗与管道环型焊缝之间的摩擦力，研究了单舱段机器人碰撞焊缝时的速度和加速度响应。由于压差式管道机器人系统涉及刚体运动、结构振动和流体力学等多学科耦合问题，上述研究模型忽略了密封皮碗的大变形、舱段与流体的相互作用以及多舱段的协同运动，难以精确预测压差式管道机器人系统的动力特性。

管内流体脉动[13-15]、外界环境振动[16]以及外部激励[17]引起的管道振动，将诱发管内流体和管道的流固耦合作用，进而影响压差式管道机器人的动力响应。本文以埋地输流管道为压差式管道机器人的运行环境，在没有爆炸冲击地震波等外部激励作用下，可忽略管道的耦合振动而将其简化为刚体，机器人的动力响应仅由管内流体与其自身的流固耦合作用决定。

耦合的欧拉-拉格朗日（Coupled Eulerian-Lagrangian，CEL）方法采用基于体积分数的流固耦合边界追踪法，在结构和流体域间进行载荷、位移、速度等信息传递，适于解决金属切削[18-19]、相互倾彻[20]、爆炸冲击[21]等大变形损伤问题，以及复杂的流固耦合问题[22-25]。本文基于CEL方法，构建压差式管道机器人柔性多体系统的流固耦合动力学模型，研究机器人在管道内的运动速度、密封皮碗的应力场、驱动压差和摩擦力等动力特性。建立多舱段压差式管道机器人的参数化模型，揭示管道焊瘤高度、弯道曲率半径和弯道倾角等几何参数对机器人平均驱动压差、平均摩擦力和密封皮碗峰值米塞斯应力等管道环境适应参数的影响规律，以期为管道机器人的巡线能力评价和设计优化提供参考。

1 基于CEL方法的流固耦合模型

压差式管道机器人由驱动舱段和若干作业舱段组成，各单元通过双万向联轴节刚性连接，如图1所示。由于管道机器人的动力特性涉及刚体运动、结构大变形和流体力学等多学科耦合问题，因而采用耦合的欧拉-拉格朗日方法求解上述流固耦合问题。管道机器人的聚氨酯密封皮碗处理为柔性部件，舱段、双万向联轴节以及管道处理为刚性部件。聚氨酯密封皮碗与管道内壁的接触摩擦系数为0.3[26]，管内流体与机器人的摩擦系数远小于密封皮碗与管道内壁的摩擦系数，因此忽略流体与管道和机器人之间的滑动摩擦[3]。

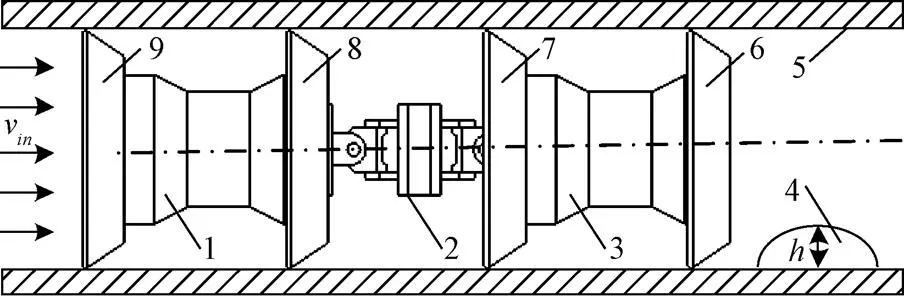
1.作业舱段 2.双万向联轴节 3.驱动舱段 4.焊瘤 5.管道 6.驱动密封皮碗1 7.驱动密封皮碗2 8.支撑密封皮碗1 9.支撑密封皮碗2

1.Operating cabin 2.Double universal joint 3.Driving cabin 4.Weld beading 5.Pipeline 6.Driving sealing cup 1 7.Driving sealing cup 2 8.Supporting sealing cup 1 9.Supporting sealing cup 2

注：为焊瘤高度，mm；v为流体入口速度，m•s-1。

Note:is the height of weld beading, mm;vis the inlet velocity of fluid, m•s-1.

图1 压差式管道机器人

Fig.1 Pipeline robot driven by differential pressure

1.1 流体域控制方程

可压缩流体介质的连续性方程为

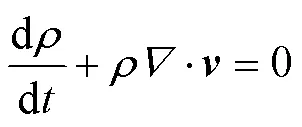
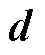
流体介质的动量守恒方程为

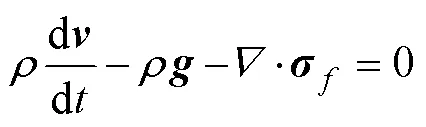
假设流体为可压缩牛顿流体，其Cauchy应力张量表示为

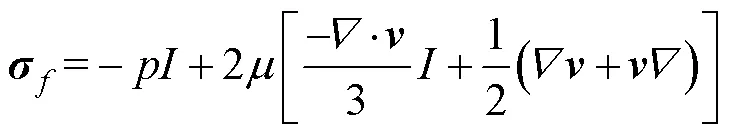
根据文献[27]，流体压强可由Mie-Gruneisen状态方程确定，即

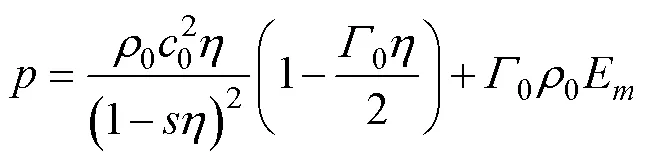
1.2 结构域控制方程

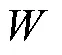
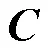
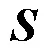
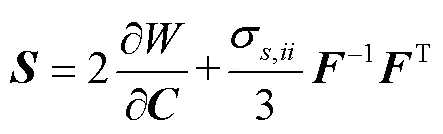
将式（5）代入式（6），把第二Piola Kirchhoff应力张量转变为Cauchy应力张量，则有：

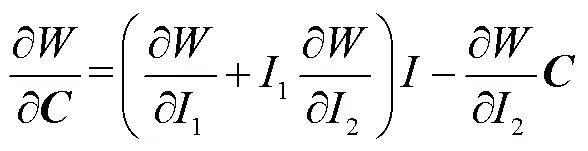
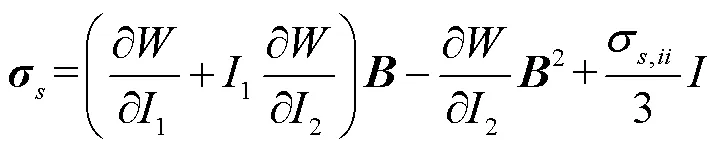
为了获得聚氨酯材料的超弹性本构参数，通过标准试验样件（图2）的单轴拉伸试验，并根据不同模型计算结果，获得材料的名义应力-名义应变曲线，如图3所示。Mooney-Rivlin模型对聚氨酯橡胶材料的试验数据拟合精度最高，模型参数为10=0.191 MPa，01=1.25 MPa。

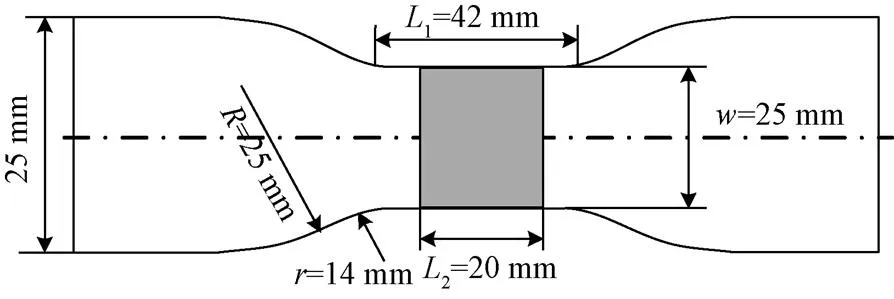
注：L1为平行长度，mm；L2为原始标距，mm；w为宽度，mm；R和r为过渡半径，mm。

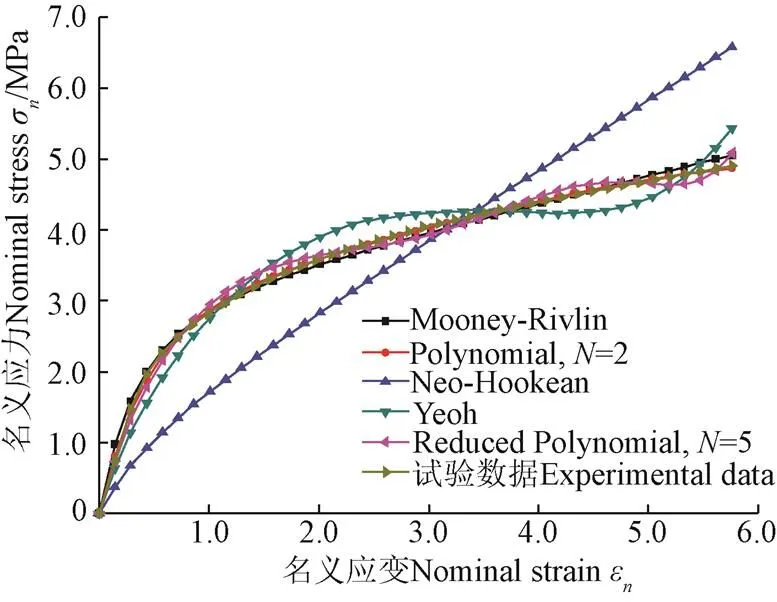
图3 聚氨酯橡胶的名义应力-应变曲线

1.3 流固耦合边界的追踪

将流体可能运动的空间离散为欧拉区域，每个欧拉单元关联一个状态变量-体积分数。当欧拉单元内充满流体时，体积分数为1，当欧拉单元内无流体填充时，体积分数为0。

由于流体介质质量守恒，体积分数满足守恒关系，则有：

注：图中数字表示欧拉单元内的流体体积分数。

Note: The numbers in the figure mean the volume fraction of the fluid in the Euler elements.

图4 流体界面的分段线性重构结果

Fig.4 Results of piecewise linear reconstruction of fluid interface

如图5所示，利用罚函数法，在结构湿表面上的单元节点与重构流体界面的锚点间放置一个虚拟弹簧，耦合非匹配的流体和结构网格，实现在结构和流体域间进行载荷、位移、速度等信息传递。跟踪结构节点与流体界面锚点的相对位移，如果结构节点倾彻流体单元，形成的耦合贯穿力将分别施加于结构单元节点和流体界面锚点上。对于结构节点有：

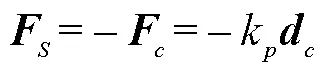
式中FS为作用于结构节点上的接触惩罚力，N；kp为虚拟弹簧的罚刚度系数，N/m，取决于结构与流体的材料特性。

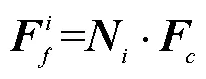
1.4 边界条件

设置流体域入口流速，指定其出口为自由边界。限制管道空间所有自由度，双万向联轴节通过旋转属性的连接单元模拟运动副。在管道内表面、流体域和机器人间施加通用接触约束。根据机器人相对于流体域的位置，计算欧拉单元的体积分数进而确定初始流固耦合界面。

1.5 模型求解

联立式（1）~（11），通过非线性有限元法构造CEL方法的数值模型，考虑到流体动量守恒方程中含有的对流项和结构的超弹性本构关系，采用Newmark显式积分格式求解上述控制方程，则有：

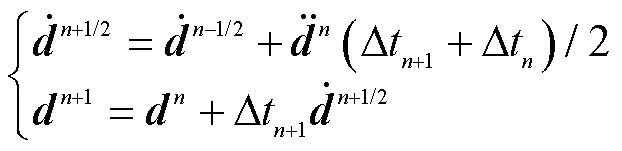
2 机器人系统的动力响应

依据文献[4]，机器人运行的弯管曲率半径变化范围为1.5～4（为管道内径，mm），1.5弯管为机器人最难通过管道，因而作为机器人运行的极限工况；3弯管则作为机器人的一般工况来评价其动力特性。机器人系统至少包含3个舱段（驱动舱段、检测舱段、作业舱段）至多5个舱段（驱动舱段、检测舱段、3个作业舱段），因此进行3舱段和5舱段工况的动力特性分析。多舱段压差式管道机器人运行于直径=200 mm的蛇形管道环境，管道入口流速为6 m/s。为了后续分析管道参数对机器人动力特性的影响，定义机器人运行的基本工况为：入口段与出口段的弯道曲率半径分别为3、1.5，两段弯道的角度=90°，焊瘤高度=0 mm。利用Newmark显式积分方法和算子劈分方法获得机器人流固耦合动力学响应，分别提取驱动舱段的运行速度（机器人速度），管道内机器人两端的驱动压差、总摩擦力（皮碗接触切应力的合力）以及密封皮碗的米塞斯应力，结果如表1和图6～9所示。

表1 不同舱段管道机器人的动力响应比较

如图6所示，由于受到弯管几何约束作用，3舱段管道机器人的密封皮碗在弯管处产生剧烈的局部挤压。由于小曲率半径弯道的运动空间更为狭小，曲率半径1.5处产生的峰值米塞斯应力达到7.445 MPa。如图7所示，机器人在启动阶段至末端舱段进入曲率半径3（0 s<<0.13 s）的过程中，运动速度呈上升趋势，最大速度达到9.1 m/s。末端舱段运动至曲率半径3弯管段中间位置（0.13 s<<0.20 s）的过程中，由于驱动压差减小、摩擦阻力增加，机器人的运动速度降至最低。当驱动舱段即将进入曲率半径1.5的弯管段（=0.21 s）时，驱动压差形成瞬时脉冲，致使机器人的运动速度瞬间跃升至峰点，随后由于摩擦阻力形成9.2 kN的瞬时脉冲作用，机器人运动速度随之降至最低。同理，在驱动舱段完全位于1.5弯管段（=0.26 s）以及完全离开1.5弯管段（=0.35 s）时，依次出现的驱动压差瞬时脉冲导致机器人速度波动显著，特别是驱动舱段离开1.5弯管段时，最大驱动压差达到1.42 MPa，机器人最大运动速度达到了9.1 m/s。

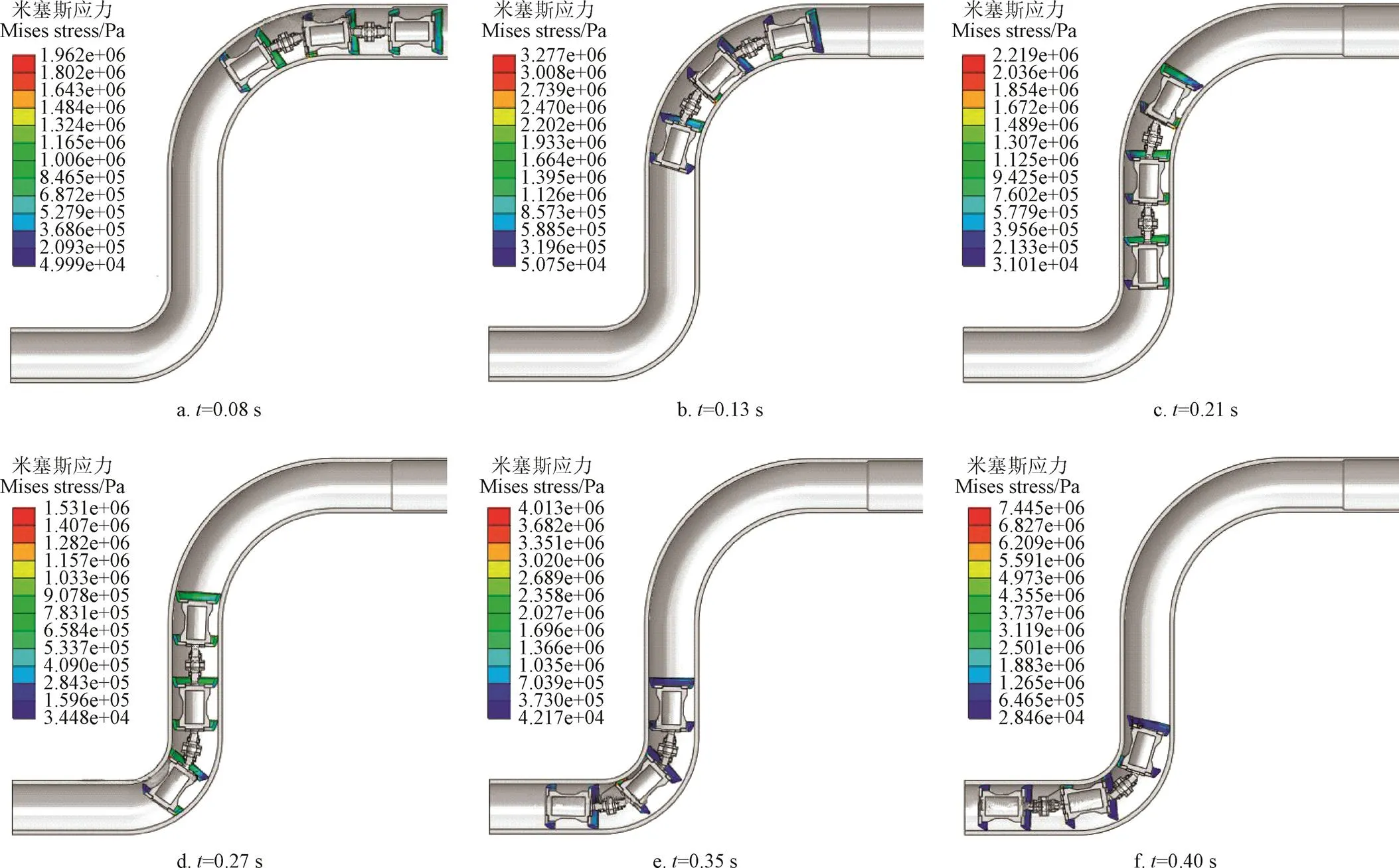
图6 3舱段压差式管道机器人密封皮碗在不同时刻的应力场

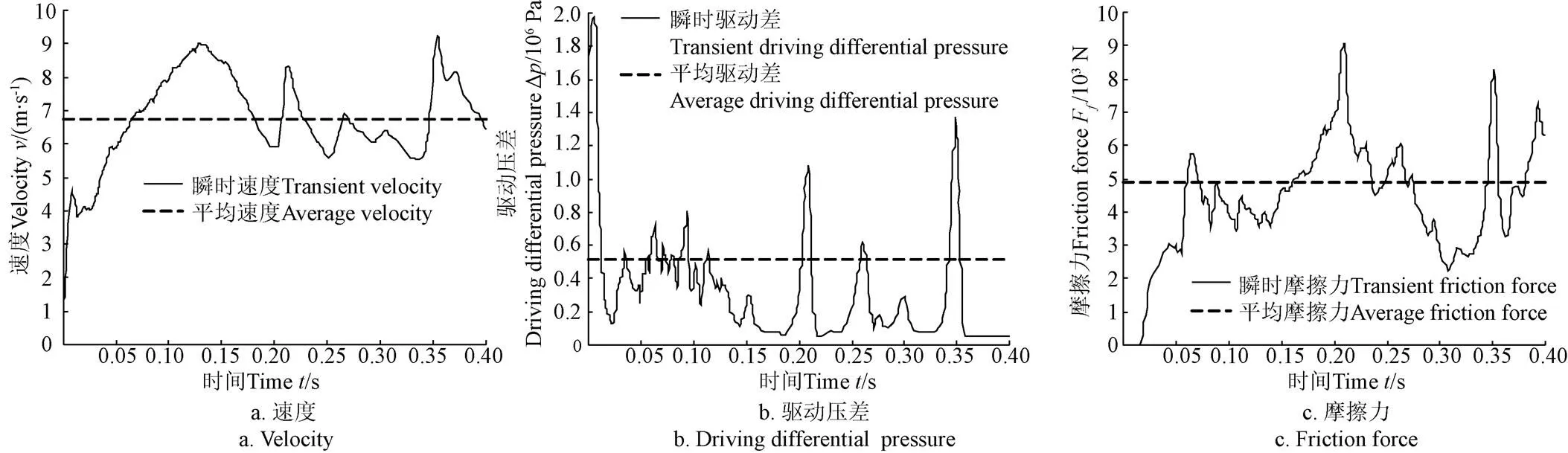
图7 3舱段压差式管道机器人的动力响应

如图8所示，5舱段管道机器人的密封皮碗的应力变化趋势与3舱段管道机器人相似。由于5舱段管道机器人与弯道的挤压作用更为强烈，形成的峰值米塞斯应力达到10.57 MPa。如图9所示，由启动阶段至末端舱段即将进入管道弯曲段（0 s<<0.24 s），机器人的运动速度呈上升趋势，峰值速度达到7.7 m/s。在机器人末端舱段即将进入3弯管段时驱动舱段则刚进入1.5弯管段（=0.37 s），此时机器人系统的负载达到最大，驱动压差峰值达到3 MPa，致使机器人运动速度跃升至最大速度8.1 m/s。驱动舱段完全位于1.5弯管段时（=0.43 s），密封皮碗与管道内壁的接触相对均匀，最大瞬时摩擦力为20.8 kN。

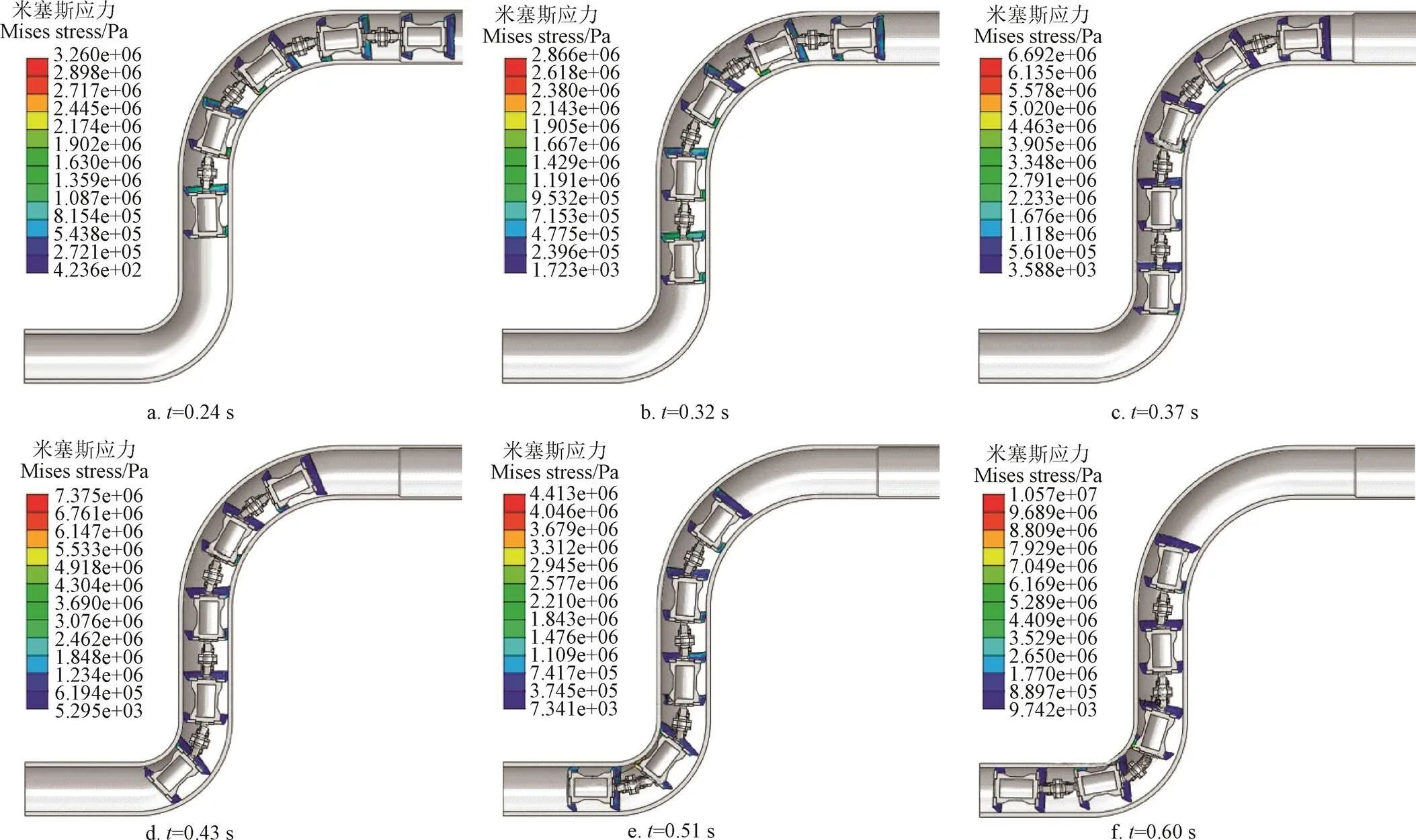
图8 5舱段压差式管道机器人密封皮碗的应力场

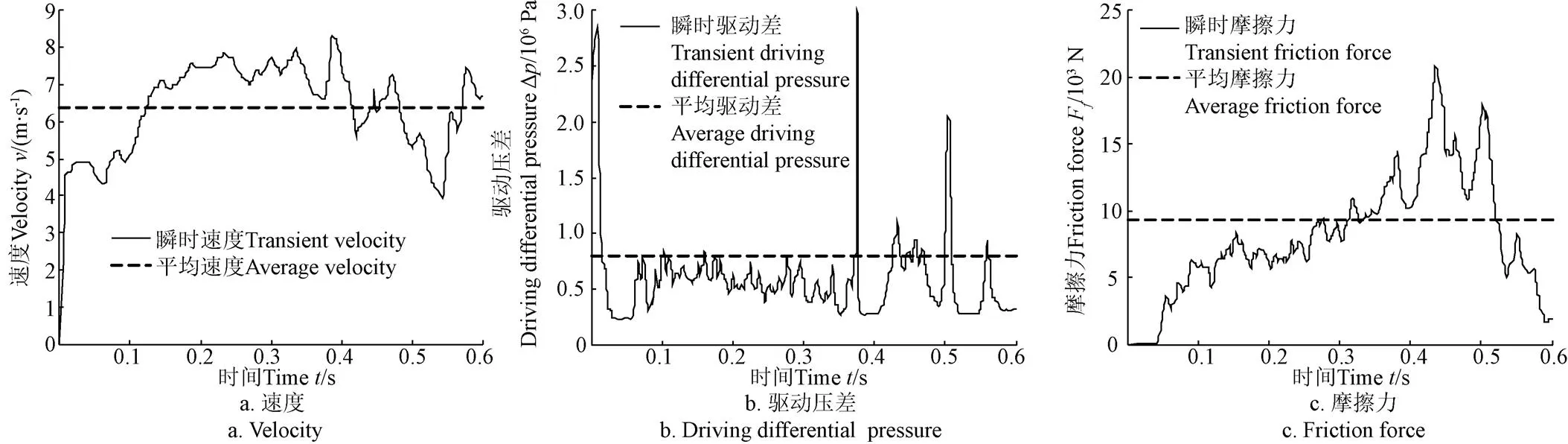
图9 5舱段压差式管道机器人的动力响应

根据表1，与3舱段机器人相比，5舱段机器人的平均速度和速度波动幅值分别降低5.3%和18.6%，但是平均驱动压差、摩擦力和峰值米塞斯应力分别增加了56.9% 、95.7%和42.0%。由此，随着舱段数量的增加，密封皮碗的变形量增加，流体需提供更大的驱动压差克服摩擦力作用，但机器人的运动平稳性有所提高。

3 管道环境适应性

为了评价管道机器人对管道环境的适应性，从外载荷与结构应力角度分析管道几何参数变化对机器人承受的平均驱动压差、平均摩擦力和密封皮碗的米塞斯应力峰值的影响，结果如图10～12和表2所示。为了对比分析管道参数对机器人动力特性的影响，定义机器人运行的基本工况为：入口段与出口段的弯道曲率半径分别为3和1.5，两段弯道的弯曲角度为90°，焊瘤高度为0。

3.1 焊瘤高度对机器人动力特性的影响

根据文献[6，10]，焊瘤呈半椭球形状，焊瘤高度=0～20 mm，其他参数与基本工况相同。因为在蛇形弯道内，曲率半径1.5的弯道段为极端运动工况，因此将焊瘤设于1.5弯道段内。如图10所示，随着焊瘤高度的增加，各舱段受到焊瘤的挤压作用，机器人系统的平均摩擦力和驱动压差显著增加，密封皮碗的米塞斯应力峰值大幅提高。对比5舱段与3舱段机器人动力特性，由于前者需要克服更大的越障阻力，因而其平均驱动压差、平均摩擦力和密封皮碗的米塞斯应力峰值均高于后者。

图10 焊瘤高度对机器人动力特性的影响

3.2 弯道曲率半径对机器人动力特性的影响

根据文献[4-5]，管道出口段的弯道曲率半径一般为300～800 mm。为便于分析，设管道机器人和管道几何参数以及运动参数与基本工况相同。管道不同出口段弯道曲率半径下管道机器人的动力特性如图11所示。由图可知，随着弯道曲率半径的增加，管道对机器人的运动约束作用减弱，机器人系统的平均驱动压差和平均摩擦力减小；此外，由于密封皮碗与管道内壁的相互作用减弱，密封皮碗的米塞斯应力峰值呈单调下降趋势。对比5舱段与3舱段机器人的动力特性可知，由于弯道约束对前者的作用强于后者，因而其平均驱动压差、平均摩擦力和密封皮碗的米塞斯应力峰值均高于后者。

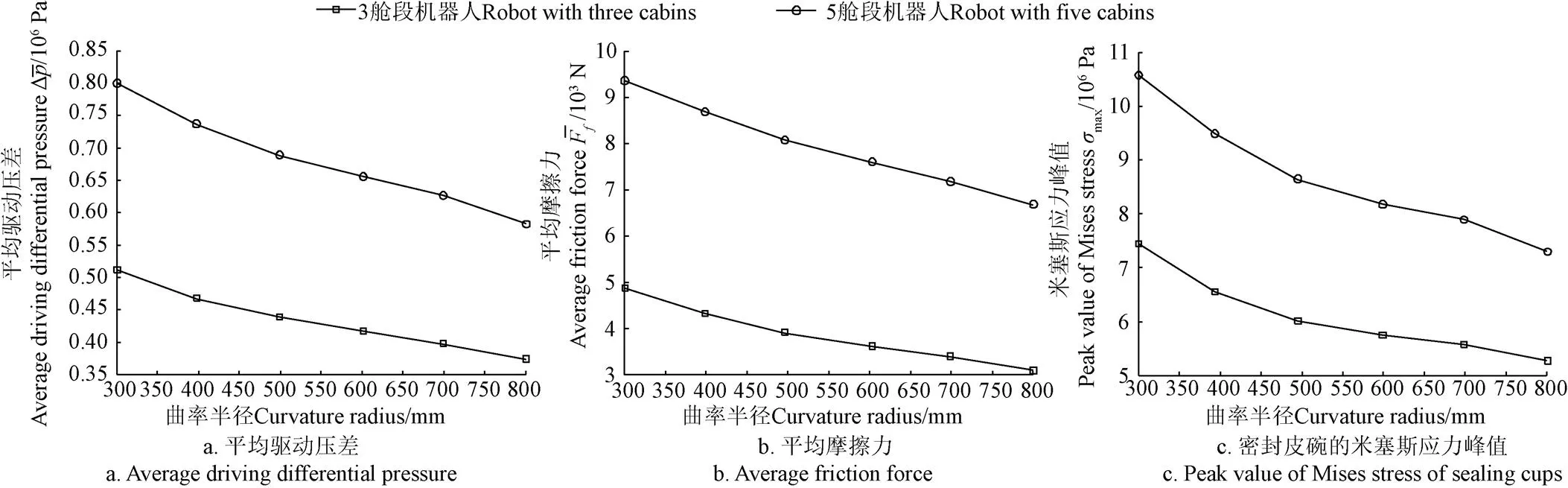
图11 管道弯曲段曲率半径对机器人动力特性的影响

3.3 管道弯曲角度对机器人动力特性的影响

根据文献[4-5]，管道的弯道角度一般0°～90°。不同管道弯曲角度下管道机器人的动力特性如图12所示。由图可知，随着管道弯曲角度的增加，管道对机器人的运动约束作用增强，机器人系统的平均驱动压差和平均摩擦力增加；此外，由于密封皮碗与管道内壁的相互作用增强，密封皮碗的米塞斯应力峰值呈单调上升趋势。对比5舱段与3舱段机器人动力特性可知，由于弯道约束对前者的作用强于后者，因而其平均驱动压差、平均摩擦力和密封皮碗的米塞斯应力峰值均高于后者。

根据图10～12，在焊瘤高度20 mm、管道弯曲角度90°、管道弯曲段曲率半径300 mm时，5舱段和3舱段机器人的平均摩擦力、平均驱动压差以及密封皮碗的米塞斯应力峰值均达到最大：5舱段机器人分别为0.98 MPa、10.61 kN和28.30 MPa，3舱段机器人分别为0.63 MPa、5.64 kN和24.16 MPa。与3舱段机器人相比，在弯道与焊瘤的联合约束作用下，5舱段机器人需要消耗更多的流体压力能克服管道的约束阻力；此外，较大的摩擦力将导致密封皮碗磨损加速，进而削弱密封性能，而过高的米塞斯应力峰值也将增加密封皮碗的脆性断裂风险。

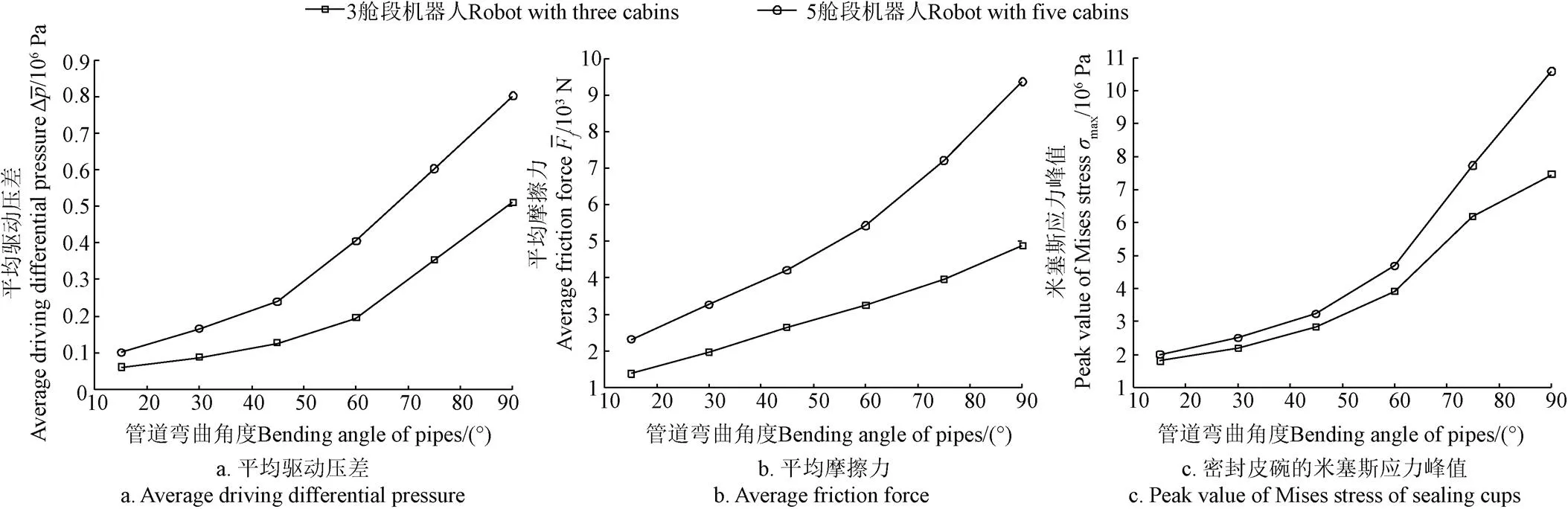
图12 管道弯曲段弯曲角度对机器人动力特性的影响

4 结 论

由于压差式管道机器人结构复杂，管内运动过程涉及流固耦合问题，其动力特性预示一直都是结构设计和实验的难点问题。本文基于CEL方法对机器人动力参数及管道几何参数对机器人管道环境适应性的影响进行了数值预测，得出如下结论：

1）与3舱段管道机器人相比，5舱段管道机器人平均速度和速度波动幅值分别降低5.3%和18.6%，但是，平均驱动压差、摩擦力和峰值米塞斯应力分别提高56.9% 、95.7%和42.0%。由此，随着舱段数量的增加，密封皮碗的变形进一步增加，流体需提供更大的驱动压差克服摩擦力作用，但是机器人系统的速度平稳性有所提高。

2）3舱段和5舱段机器人在管道焊瘤高度为20 mm、弯道角度为90°和弯道曲率半径为300 mm时，两者的平均摩擦力、平均驱动压差以及密封皮碗的米塞斯应力峰值均达到最大。前者的上述指标分别为0.63 MPa、5.64 kN和24.16 MPa，后者的上述指标分别为0.98 MPa、10.61 kN和28.30 MPa。由此，与3舱段机器人相比，在弯道与焊瘤约束的联合作用下，5舱段机器人在此危险工况下则消耗更多的流体压力能克服管道的约束阻力；密封皮碗更易于磨损而削弱了密封性能以及面临更高的脆性断裂风险。

综上，针对不同的管道环境，利用所建立的机器人计算模型优化多舱段机器人的结构参数，改善机器人的动力特性，对于提高机器人的管道环境适应性和巡线能力具有重要的理论与工程意义。

[1] 刘清友. 油气管道机器人技术现状及发展趋势[J]. 西华大学学报：自然科学版，2016，35(1)：1-6.

Liu Qingyou. Research status and development tendency of the oil and gas in-pipe robot[J]. Journal of Xihua University: Natural Science Edition, 2016, 35(1): 1-6. (in Chinese with English abstract)

[2] 郭静波，皇甫奋宇，肖承翔，等. 流固耦合式管道检测机器人自主发电系统[J]. 清华大学学报：自然科学版，2014，54(9)：1155-1160.

Guo Jingbo, Huangfu Fenyu, Xiao Chengxiang, et al. Fluid-solid coupling based power generating system for a self-powered pipeline robot[J]. Journal of Tsinghua University: Science & Technology, 2014, 54(9): 1155-1160. (in Chinese with English abstract)

[3] Patricio R A C, Baptista R M, Rachid B F. Numerical simulation of pig motion in gas and liquid pipelines using the Flux-Corrected Transport method[J]. Journal of Petroleum Science and Engineering, 2020, 189(6): 1-14.

[4] Liu Chang, Wei Yungang, Cao Yuguang, et al. Traveling ability of pipeline inspection gauge (PIG) in elbow under different friction coefficients by 3D FEM[J]. Journal of Natural Gas Science and Engineering, 2020, 75(3): 1-12.

[5] Chen Jianheng, He Limin, Luo Xiaoming, et al. Characterization of bypass pig velocity in gas pipeline: an experimental and analytical study[J]. Journal of Natural Gas Science and Engineering, 2020, 73(1): 1-12.

[6] Zhang Hang, Zhang Shimin, Liu Shuhai, et al. Collisional vibration of PIGs (pipeline inspection gauges) passing through girth welds in pipelines[J]. Journal of Natural Gas Science and Engineering, 2017, 37(1): 15-28.

[7] Lesani M, Rafeeyan M, Sohankar A. Dynamic analysis of small Pig through two and three dimensional liquid pipeline[J]. Journal of Applied Fluid Mechanics, 2012, 5(2): 75-83.

[8] Malihe Mirshamsi, Mansour Rafeeyan. Dynamic analysis and simulation of long pig in gas pipeline[J]. Journal of Natural Gas Science and Engineering, 2015, 23(3): 294-303.

[9] Liang Z, He H G, Cai W L. Speed simulation of bypass hole PIG with a brake unit in liquid pipe[J]. Journal of Natural Gas Science and Engineering, 2017, 42(6): 40-47.

[10] Zhang Hang, Zhang Shimin, Liu Shuhai, et al. Measurement and analysis of friction and dynamic characteristics of PIG’s sealing disc passing through girth weld in oil and gas pipeline[J]. Measurement, 2015 , 64(3): 112-122

[11] Zhu X, Zhang S, Li X, et al. Numerical simulation of contact force on bi-directional pig in gas pipeline: At the early stage of pigging[J]. Journal of Natural Gas Science and Engineering, 2015, 23(3): 127-138.

[12] Zhu Xiaoxiao, Wang Deguo, Yeung Hoi, et al. Comparison of linear and nonlinear simulations of bidirectional pig contact forces in gas pipelines[J]. Journal of Natural Gas Science and Engineering, 2015, 27(11): 151-157.

[13] 赵江，俞建峰，楼琦. 基于流固耦合的T型管振动特性分析[J]. 振动与冲击，2019，38(22)：117-123.

Zhao Jiang, Yu Jianfeng, Lou Qi. Modal analysis of T-shaped pipes based on a fluid-solid interaction model[J]. Journal of Vibration and Shock, 2019, 38(22): 117-123. (in Chinese with English abstract)

[14] 周知进，何星，戴哲冰. 不同曲率情况下的液压管道流固耦合特性仿真研究[J]. 振动与冲击，2017，36(5)：214-220.

Zhou Zhijin, He Xing, Dai Zhebing. Simulation for fluid-solid interaction characteristics of hydraulic pipes with different curvatures[J]. Journal of Vibration and Shock, 2017, 36(5): 214-220. (in Chinese with English abstract)

[15] 张建伟，王涛，曹克磊，等. 基于流固耦合效应的梯级泵站输水管道振动特性分析[J]. 农业机械学报，2017，48(3)：134-140.

Zhang Jianwei, Wang Tao, Cao Kelei, et al. Analysis of water pipeline vibration characteristics in cascade pumping station based on fluid-solid coupling interaction[J]. Transactions of the Chinese Society for Agricultural Machinery, 2017, 48(3): 134-140. (in Chinese with English abstract)

[16] 丁宇奇，戴子威，芦烨，等. 爆炸地震波作用下埋地管道流固耦合动力响应研究[J]. 压力容器，2019，36(11)：34-43.

Ding Yuqi, Dai Ziwei, Lu Ye, et al. Study on fluid-structure coupling dynamic response of buried pipeline under action of explosive seismic waves[J]. Pressure Vessel Technology, 2019, 36(11): 34-43. (in Chinese with English abstract)

[17] 周知进，陈雄，康红军，等. 海流冲击对深海采矿装备液压管道流固耦合振动的影响[J]. 噪声与振动控制，2015，35(2)：7-10.

Zhou Zhijin, Chen Xiong, Kang Hongjun, et al. Influence of ocean current impact on fluid-structure coupled vibration of deep-sea mining equipment’s hydraulic pipelines[J]. Noise and Vibration Control, 2015, 35(2): 7-10. (in Chinese with English abstract)

[18] Ducobu F, Rivière-Lorphèvre E, Filippi E. Finite element modelling of 3D orthogonal cutting experimental tests with the Coupled Eulerian-Lagrangian (CEL) formulation[J]. Finite Elements in Analysis & Design, 2017, 134(10): 27-40.

[19] Ducobu F, Rivière-Lorphèvre E, Filippi E. Application of the Coupled Eulerian-Lagrangian (CEL) method to the modeling of orthogonal cutting[J]. European Journal of Mechanics, 2016, 59(9/10): 58-66.

[20] Sherburn J A, Hammons M I, Roth M J. Modeling finite thickness slab perforation using a coupled Eulerian- Lagrangian approach[J]. International Journal of Solids & Structures, 2014, 51(25/26): 4406-4413.

[21] Mittal V, Chakraborty T, Matsagar V. Dynamic analysis of liquid storage tank under blast using coupled Euler-Lagrange formulation[J]. Thin-Walled Structures, 2014, 84(84): 91-111

[22] 李刚，唐霄汉，艾森，等. 大型整流罩地面分离仿真预示与试验研究[J]. 宇航学报，2015，36(7)：833-839.

Li Gang, Tang Xiaohan, Ai Sen, et al. Simulation and experimental research on ground separation of a large-scale payload fairing[J]. Journal of Astronautics, 2015, 36(7): 833-839. (in Chinese with English abstract)

[23] 姚小虎，黄愉太，欧智成，等. 基于CEL算法的水陆两栖飞机水上降落动力特性分析[J]. 华南理工大学学报：自然科学版，2015，43(6)：110-115.

Yao Xiaohu, Huang Yutai, Ou Zhicheng, et al. CEL algorithm-based analysis of dynamic characteristics of amphibious aircraft landing on water [J]. Journal of South China University of Technology: Natural Science Edition, 2015, 43(6): 110-115. (in Chinese with English abstract)

[24] 马子远，俞小莉，黄钰期，等. 基于CEL算法的发动机润滑液瞬态振荡过程可视化研究[J]. 振动与冲击，2018，37(1)：72-76.

Ma Ziyuan, Yu Xiaoli, Huang Jueqi, et al. CEL algorithm-based visualization simulation of the transient oscillation of engine lubricant[J]. Journal of Vibration and Shock, 2018, 37(1): 72-76. (in Chinese with English abstract)

[25] Y Shi, G Xu, P Wei. Rotor wake and flow analysis using a coupled Eulerian-Lagrangian method[J]. Engineering Applications of Computational Fluid Mechanics, 2016, 10(1): 386-404.

[26] 田雨，张杰，韦永继，等. 聚氨酯弹性体摩擦系数影响因素探讨[J]. 聚氨酯工业，2002，17(1)：37-40

Tian Yu, Zhang Jie, Wei Yongji, et al. The discussion on factors influencing the friction coefficient of polyurethane Elastomers[J]. Engineering Mechanics, 2002, 17(1): 37-40. (in Chinese with English abstract)

[27] Shyue Keh-ming. A fluid-mixture type algorithm for compressible multicomponent flow with Mie-Gruneisen equation of state[J]. Journal of computational Physics, 2001, 171(2): 678-707.

[28] 胡小玲，刘秀，李明，等. 炭黑填充橡胶超弹性本构模型的选取策略[J]. 工程力学，2014，31(5)：34-42.

Hu Xiaoling, Liu Xiu, Li Ping, et al. Selection strategies of hyperelastic constitutive models for carbon black filled rubber[J]. Engineering Mechanics, 2014, 31(5): 34-42. (in Chinese with English abstract)

[29] 刘礼华，王蒂，欧珠光，等. 橡胶类止水材料超弹性性能的研究与应用[J]. 四川大学学报：工程科学版，2011，43(4)：199-204.

Liu Lihua, Wang Di, Ou Zhuguang, et al. Application and research on the hyper-elastic properties for rubber-like water-stop material[J]. Journal of Sichuan University: Engineering Science Edition, 2011, 43(4): 199-204. (in Chinese with English abstract)

Construction of fluid-solid coupling model of flexible multibody system for pipeline robots driven by differential pressure

Teng Xiaoyan1, Jiang Xudong2※, Ma Rui1

(1.150001,;2.150080,)

The movement of the differential pressure pipeline robots in the pipeline driven by the fluid belongs to the complex fluid structure coupling dynamics problem. It is of great engineering significance to analyze the dynamic responses of the robots and evaluate the ability of the robot to patrol the pipeline by numerical simulation. Based on the coupled Eulerian Lagrangian (CEL) method, a fluid structure coupling dynamic model of the flexible multibody system for pipeline robots driven by differential pressure was constructed in this paper. The govening equations of the pipeline robots and its surrounding compressible Newton’s fluid were derived and represented with CEL frame. In order to efficiently describe the experienced large deformation process of the sealing cups, two-parameter Mooney-Rivilin model was used and its coefficients was obtained based on the uniaxial tensile tests of polyurethane. Based on the method of immersion boundary, the volume fraction in each fluid element contained wass used to track the fluid boundary by piecewise linear interface calculation. A novel penalty coupling method was used to simulate the interaction of the fluid with the robot by implementing a virtual spring bwteen the nodes at structural surface element and the anchor points at the fluid interface. The adaptability of the robot to the pipeline environment was evaluated by the average driving pressure difference, the average friction and the Mises stress peak value of the sealing cup. The parametric model of the pipeline robots with three and five cabins were developed to investigate the influence of pipeline geometrical parameters on the robots adaptability to internal pipeline environment. The numerical analysis results indicated that compared with the pipeline robot with three cabins, the average velocity and amplitude of velocity of the pipeline robot with five cabins were decreased by 5.3% and 18.6%,. and the running stability was better than that of the pipeline robot with three cabins, the average driving different pressure, friction force and peak values of mises stress of the sealing cups for the the pipeline robot with five cabins increased by 56.9%, 95.7% and 42.0% compared with the pipeline robot with three cabins, which showed that with the increase of the numbers of the cabins, the deformation of the sealing cup increased further, and the fluid needed to provide a larger driving pressure difference to overcome the friction, but the running stability of the robot was improved. For the pipeline robots with three and five cabins, the average friction force, the average driving pressure difference and the Mises stress peak value of sealing cups were all the maximum when the height of weld beading was 20 mm, the bending angle of bending section was 90° and the radius of curvature was 300 mm, thats of the pipeline robot with three cabins were 0.63 MPa, 5.64 kN and 24.16 MPa, respectivly, and 0.98 MPa, 10.61 kN and 28.30 MPa for the pipeline robot with five cabins Therefore, compared with the pipeline robot with three cabins, the pipeline robot with five cabins need to consume more fluid pressure energy to overcome the constraint resistance of the pipeline under dangerous conditions, the sealing cup is easier to wear, which weakens the sealing performance and has higher risk of brittle fracture. The research results can provide reference for the evaluation and design optimization of pipeline robot.

robots; numerical analysis; fluid-solid interaction; flexible multibody system; pipeline robot driven by different pressure; dynamic characteristics

滕晓艳，江旭东，马睿. 压差式管道机器人柔性多体系统流固耦合模型构建[J]. 农业工程学报，2020，36(8)：31-39.doi：10.11975/j.issn.1002-6819.2020.08.004 http://www.tcsae.org

Teng Xiaoyan, Jiang Xudong, Ma Rui. Construction of fluid-solid coupling model of flexible multibody system for pipeline robots driven by differential pressure[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2020, 36(8): 31-39. (in Chinese with English abstract) doi：10.11975/j.issn.1002-6819.2020.08.004 http://www.tcsae.org

2019-11-10

2020-03-23

国家自然科学基金项目（51505096）；黑龙江省自然科学基金项目（QC2016056）

滕晓艳，博士，副教授，主要从事机械结构动力学与拓扑优化设计。Email：tengxiapyan@hrbeu.edu.cn

江旭东，博士，副教授，主要从事复杂结构的流固耦合动力学分析与设计优化。Email：xudongjiang@sina.com

10.11975/j.issn.1002-6819.2020.08.004

TH113.1; TH242.3

A

1002-6819(2020)-08-0031-09